4.3: الكثافة في حيود الشق الواحد
- Page ID
- 196578
في نهاية هذا القسم، ستكون قادرًا على:
- احسب الكثافة بالنسبة إلى الحد الأقصى المركزي لقمم الحيود أحادية الشق
- احسب الكثافة بالنسبة إلى الحد الأقصى المركزي لنقطة عشوائية على الشاشة
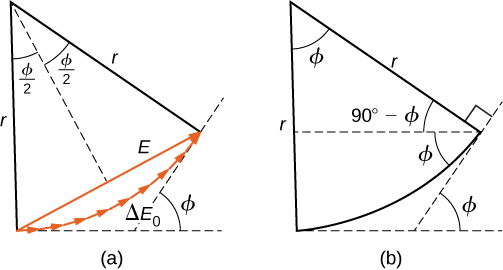
لحساب شدة نمط الحيود، نتبع طريقة الطور المستخدمة في العمليات الحسابية مع دوائر التيار المتردد في دوائر التيار المتردد. إذا اعتبرنا أن هناك مصادر\(N\) Huygens عبر الشق الموضح سابقًا، مع فصل كل مصدر بمسافة A/n عن جيرانه المجاورين، فإن فرق المسار بين الموجات من المصادر المجاورة التي تصل إلى النقطة العشوائية\(P\) على الشاشة هو\((a/N) \, \sin \theta\). هذه المسافة تعادل فرق الطور البالغ\((2\pi a/\lambda N) \, \sin \, \theta\). يظهر مخطط الطور للموجات القادمة إلى النقطة التي يظهر موضعها الزاوي في الشكل\(\PageIndex{1}\).\(\theta\) سعة الطور لكل موجة من موجات Huygens هي\(\Delta E_0\)، سعة الطور الناتج هي\(E\)، وفرق الطور بين الموجات من المصدر الأول والأخير هو
\[\phi = \left(\dfrac{2\pi}{\lambda}\right) \, a \, \sin \theta. \nonumber \]
مع\(N → ∞\) ذلك، يقترب مخطط الطور من قوس دائري بالطول\(N \Delta E_0\) ونصف القطر\(r\). نظرًا لأن طول القوس هو\(N \Delta E_0\) لأي جزء\(ϕ\)، يجب أن ينخفض نصف قطر\(r\) القوس كلما\(ϕ\) زاد (أو بشكل مكافئ، حيث تشكل المحاور حلزونات أكثر إحكامًا).
يظهر مخطط الطور لـ = 0 (مركز نمط الحيود) في الشكل\(\PageIndex{1a}\) باستخدام N = 30. في هذه الحالة، يتم وضع وحدات الطور من طرف إلى طرف في خط مستقيم من الطول\(N \Delta E_0\)، وينتقل نصف القطر r إلى ما لا نهاية، ويكون الناتج له قيمته القصوى\(E = N\Delta E_0\). يمكن الحصول على شدة الضوء باستخدام العلاقة\(I = \dfrac{1}{2} c \epsilon_0 E^2\) من الموجات الكهرومغناطيسية. ثم تكون شدة الحد الأقصى
\[I_0 = \dfrac{1}{2} c\epsilon_0 (N \Delta E_0)^2 = \dfrac{1}{2\mu_0 c}(N\Delta E_0)^2, \nonumber \]
أين\(\epsilon_0 = 1/\mu_0 c^2\). تظهر مخططات الطور لأول صفرين من نمط الحيود في الشكل\(\PageIndex{1b}\) والشكل\(\PageIndex{1d}\). في كلتا الحالتين، يتم إضافة وحدات الطور إلى الصفر، بعد الدوران عبر\(\phi = 2\pi\) الراد لـ m = 1 و\(4 \pi\) rad لـ m = 2.
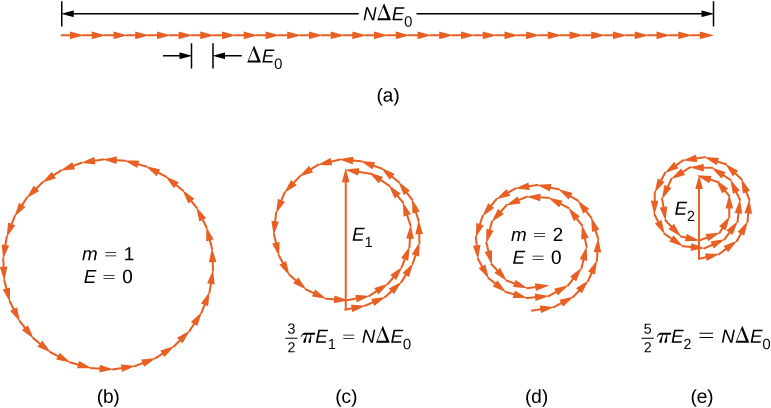
يتم تمثيل الحد الأقصى التاليين بعد الحد الأقصى المركزي بمخططات الطور للأجزاء (ج) و (هـ). وفي الجزء (ج)، تناوبت أجهزة الحفر على\(\phi = 3\pi\) طول الطريق وشكلت نتيجة لذلك متدرج من حيث الحجم\(E_1\). طول القوس الذي تشكله أجهزة الطور هو\(N\Delta E_0\). نظرًا لأن هذا يتوافق مع 1.5 دورة حول دائرة قطرها\(E_1\)، فلدينا
\[\dfrac{3}{2} \pi E_1 = N \Delta E_0, \nonumber \]
وبالتالي
\[E_1 = \dfrac{2N\Delta E_0}{3\pi} \nonumber \]
و
\[I_1 = \dfrac{1}{2\mu_0 c}E_1^2 = \dfrac{4(N\Delta E_0)^2}{(9\pi^2)(2\mu_0c)} = 0.045 I_0, \nonumber \]
حيث
\[I_0 = \dfrac{(N\Delta E_0)^2}{2\mu_0 c}. \nonumber \]
في الجزء (هـ)، تم تدوير المراوح عبر\(\phi = 5\pi\) راد، وهو ما يعادل 2.5 دورة حول دائرة قطرها\(E_2\) وطول القوس\(N\Delta E_0\). ينتج عن هذا\(I_2 = 0.016 I_0\). يتم ترك الإثبات كتمرين للطالب (التمرين 4.119).
وتتوافق هاتان الحدمتان في الواقع مع قيم التي تقل قليلاً عن\(3\pi\)\(5\pi\) راد وراد. نظرًا لأن الطول الإجمالي لقوس مخطط الطور يكون دائمًا\(N \Delta E_0\)، فإن نصف قطر القوس يتناقص كلما\(ϕ\) زاد. ونتيجة لذلك، تبين\(E_1\) أنها أكبر قليلاً بالنسبة للأقواس التي لم تلتف تمامًا عبر\(3\pi\) الراد والراد\(5\pi\)، على التوالي.\(E_2\) يتم فحص القيم الدقيقة\(ϕ\) للحد الأقصى في التمرين 4.120. عند حل هذه المشكلة، ستجد أنها أقل من... لكنها قريبة جدًا من\(\phi = 3\pi, \, 5\pi, \, 7\pi,\)... اقرأ.
لحساب الكثافة عند نقطة عشوائية\(P\) على الشاشة، نعود إلى مخطط الطور الخاص بالشكل\(\PageIndex{1}\). بما أن القوس يقترب من الزاوية في مركز الدائرة،
\[N\Delta E_0 = r\phi \label{eq10} \]
و
\[\sin \left(\dfrac{\phi}{2}\right) = \dfrac{E}{2r}. \label{eq11} \]
\(E\)أين سعة الحقل الناتج. حل المعادلة\ ref {eq11}\(E\) ثم استبدالها\(r\) بالمعادلة\ ref {eq10}، نجد
\[\begin{align*} E &= 2r \, \sin \, \dfrac{\phi}{2} \\[5pt] &= 2\dfrac{N\Delta E_0}{\phi} \sin \, \dfrac{\phi}{2}. \end{align*} \nonumber \]
تعريف الآن
\[\beta = \dfrac{\phi}{2} = \dfrac{\pi a \, \sin \, \theta}{\lambda} \label{4.2} \]
نحصل على
\[E = N\Delta E_0 \dfrac{\sin \, \beta}{\beta} \label{eq15} \]
تربط المعادلة\ ref {eq15} سعة الحقل الناتج في أي نقطة في نمط الحيود بالسعة\(N \Delta E_0\) عند الحد الأقصى المركزي. تتناسب الكثافة مع مربع السعة، لذلك
\[I = I_0 \left(\dfrac{\sin \, \beta}{\beta}\right)^2 \label{eq20} \]
\(I_0 = (N\delta E_0)^2/2\mu_0 c\)أين الكثافة في مركز النمط.
بالنسبة للحد الأقصى المركزي، = 0، β هي أيضًا صفر ونرى من قاعدة l'Hôpital ذلك\(\lim_{\beta \rightarrow 0}(sin \, \beta/\beta) = 1\)، وهكذا\(lim_{\phi \rightarrow 0}I = I_0\). بالنسبة للحد الأقصى التالي،\(\phi = 3\pi\) rad، لدينا\(\beta = 3\pi/2\) rad وعندما يتم استبداله في المعادلة\ ref {eq20}، ينتج
\[I_1 = I_0 \left(\dfrac{\sin \, 3\pi/2}{3\pi/2}\right)^2 = 0.045 I_0, \nonumber \]
بما يتفق مع ما وجدناه سابقًا في هذا القسم باستخدام أقطار ومحيط مخططات الطور. يؤدي استبدال\(\phi = 5\pi\) rad في المعادلة\ ref {eq20} إلى نتيجة مماثلة لـ\(I_2\).
يظهر رسم المعادلة\ ref {eq20} في الشكل\(\PageIndex{3}\) وأسفله مباشرة صورة لنمط الحيود الفعلي. لاحظ أن القمة المركزية أكثر سطوعًا من غيرها، وأن أصفار النموذج تقع في تلك النقاط حيث يحدث\(sin \, \beta = 0\) ذلك عند\(\beta = m\pi\) راد. هذا يتوافق مع
\[\dfrac{\pi a \, \sin \theta}{\lambda} = m\pi, \nonumber \]
أو
\[a \, \sin \, \theta = m \lambda, \nonumber \]
التي استخلصناها من أجل التداخل المدمر لشق واحد سابقًا.
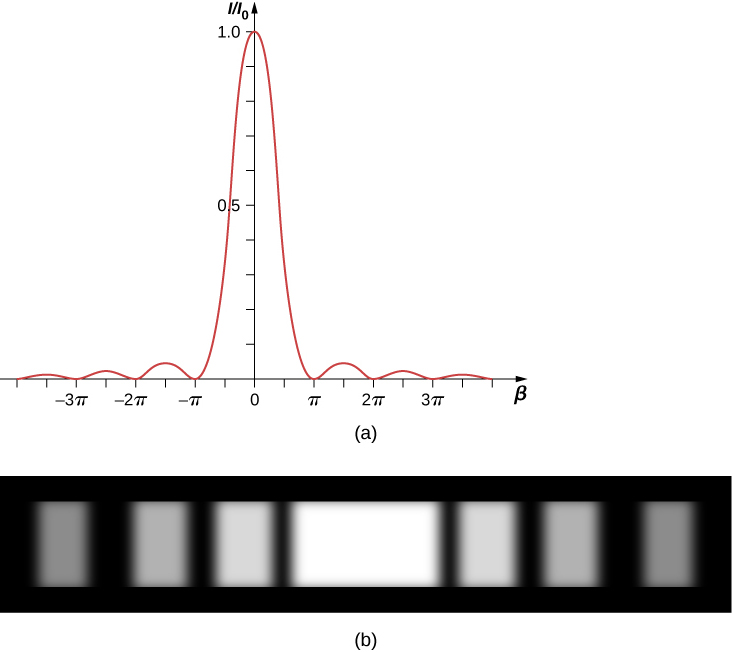
يمر ضوء طوله الموجي ٥٥٠ نانومترًا عبر شق بعرض ٢٫٠٠ ميكرومتر وينتج نمط حيود مشابه للنمط الموضح في الشكل\(\PageIndex{3a}\).
- ابحث عن مواقع أول درجتين صغيرتين بدلالة الزاوية من الحد الأقصى المركزي.
- حدد الكثافة بالنسبة إلى الحد الأقصى المركزي عند نقطة تقع في منتصف المسافة بين هذين الحدين الأدني.
إستراتيجية
يتم إعطاء الحد الأدنى من خلال المعادلة 4.2.1،\(a \, sin \, \theta = m\lambda\). الحد الأدنى الأولان هما لـ m = 1 و m = 2. يمكن استخدام المعادلة\ ref {eq20} والمعادلة\ ref {4.2} لتحديد الكثافة بمجرد حساب الزاوية.
الحل
- يعطينا حل المعادلة 4.2.1 لـ\(\theta_m = \sin^{-1}(m\lambda/a)\)، بحيث
\[\theta_1 = \sin^{-1} \left(\dfrac{(+1)(550 \times 10^{-9} m)}{2.00 \times 10^{-6}m}\right) = +16.0° \nonumber \]
و\[\theta_2 = \sin^{-1} \left(\dfrac{(+2)(550 \times 10^{-9}m)}{2.00 \times 10^{-6}m}\right) = +33.4°. \nonumber \]
- نقطة منتصف الطريق بين\(\theta_1\) و\(\theta_2\) هي
\[\theta = (\theta_1 + \theta_2) /2 = (16.0° + 33.4°)/2 = 24.7°. \nonumber \]
تعطي المعادلة\ المرجع {4.2}
\[\beta = \dfrac{\pi a \, sin \, \theta}{\lambda} = \dfrac{\pi (2.00 \times 10^{-6}m) \, \sin \, (24.7°)}{(550 \times 10^{-9}m)} = 1.52\pi \, or \, 4.77 \, rad. \nonumber \]
من المعادلة\ ref {eq20}، يمكننا الحساب
\[\dfrac{I}{I_0} = \left(\dfrac{\sin \, \beta}{\beta}\right)^2 = \left(\dfrac{\sin \, (4.77)}{4.77}\right)^2 = \left(\dfrac{-0.9985}{4.77}\right)^2 = 0.044. \nonumber \]
الأهمية
هذا الموضع، الذي يقع في منتصف المسافة بين حدين صغيرين، قريب جدًا من موقع الحد الأقصى أو المتوقع بالقرب\(\beta = 3\pi/2\) منه أو\(1.5\pi\).
بالنسبة للتجربة في المثال\(\PageIndex{1}\)، في أي زاوية من المركز هي الحد الأقصى الثالث وما شدتها بالنسبة إلى الحد الأقصى المركزي؟
- إجابة
-
\(74.3^o\)،\(0.0083 I_0\)
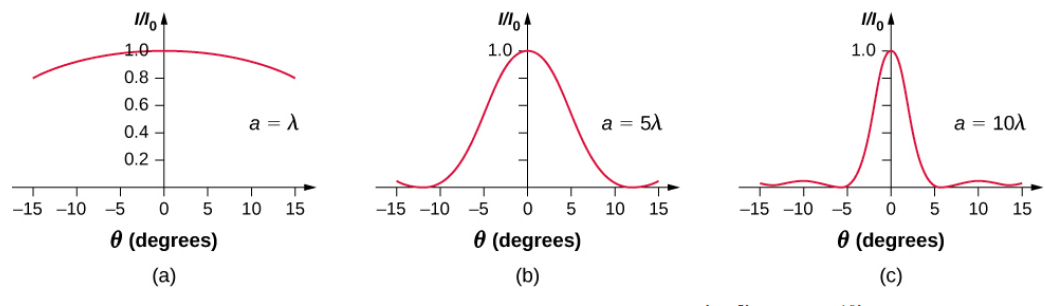
إذا كان عرض الشق\(a\) متغيرًا، يتغير توزيع الكثافة، كما هو موضح في الشكل\(\PageIndex{4}\). يتم توزيع القمة المركزية على المنطقة من\(sin \, \theta = -\lambda/a\) إلى\(sin \, \theta = +\lambda/a\). بالنسبة لـ الصغيرة، يتوافق هذا مع العرض الزاوي\(\Delta \theta \approx 2\lambda /a\). وبالتالي، تؤدي الزيادة في عرض الشق إلى انخفاض في عرض الذروة المركزية. بالنسبة للشق الذي يحتوي على》، تكون الذروة المركزية حادة جدًا، بينما إذا كانت a ≈》، فإنها تصبح واسعة جدًا.
يمكن أن تتطلب تجربة الحيود في البصريات الكثير من التحضير ولكن هذه المحاكاة من قبل Andrew Duffy لا توفر فقط إعدادًا سريعًا ولكن أيضًا القدرة على تغيير عرض الشق على الفور. قم بتشغيل المحاكاة وحدد «شق واحد». يمكنك ضبط عرض الشق ورؤية التأثير على نمط الحيود على الشاشة وكرسم بياني.


