4.2: حيود الشق الواحد
- Page ID
- 196566
في نهاية هذا القسم، ستكون قادرًا على:
- اشرح ظاهرة الحيود والظروف التي يتم ملاحظتها فيها
- وصف الحيود من خلال شق واحد
بعد المرور عبر فتحة ضيقة (فتحة)، تميل الموجة المنتشرة في اتجاه معين إلى الانتشار. على سبيل المثال، يمكن سماع الموجات الصوتية التي تدخل الغرفة من خلال باب مفتوح حتى لو كان المستمع في جزء من الغرفة حيث تملي هندسة انتشار الأشعة أنه يجب أن يكون هناك صمت فقط. وبالمثل، يمكن أن تنتشر موجات المحيط التي تمر عبر فتحة في كاسر الأمواج في جميع أنحاء الخليج من الداخل. (الشكل\(\PageIndex{1}\)). يعد انتشار وانحناء الصوت وموجات المحيط مثالين على الحيود، وهو انحناء الموجة حول حواف الفتحة أو العائق - وهي ظاهرة تظهرها جميع أنواع الأمواج.

إن انحراف الموجات الصوتية واضح لنا لأن الأطوال الموجية في المنطقة المسموعة هي تقريبًا نفس حجم الأجسام التي تواجهها، وهو شرط يجب استيفاؤه إذا أريد ملاحظة تأثيرات الحيود بسهولة. نظرًا لأن الأطوال الموجية للضوء المرئي تتراوح من 390 إلى 70 نانومتر تقريبًا، فإن معظم الأجسام لا تحيد الضوء بشكل كبير. ومع ذلك، تحدث حالات تكون فيها الفتحات صغيرة بما يكفي لملاحظة انحراف الضوء. على سبيل المثال، إذا وضعت إصبعي المنتصف والسبابة بالقرب من بعضهما البعض ونظرت من خلال الفتحة إلى مصباح كهربائي، يمكنك رؤية نمط حيود واضح نوعًا ما، يتكون من خطوط فاتحة وداكنة تسير بالتوازي مع أصابعك.
الحيود من خلال شق واحد
يُشكِّل الضوء المار عبر شق واحد نمط الحيود الذي يختلف نوعًا ما عن الأنماط المتكونة من الشقوق المزدوجة أو حواجز الحيود، التي ناقشناها في الفصل الخاص بالتداخل. \(\PageIndex{2}\)يوضح الشكل نمط الحيود أحادي الشق. لاحظ أن الحد الأقصى المركزي أكبر من الحد الأقصى على كلا الجانبين وأن الكثافة تتناقص بسرعة على كلا الجانبين. في المقابل، ينتج محزوز الحيود خطوطًا متباعدة بشكل متساوٍ تخفت ببطء على جانبي المركز.
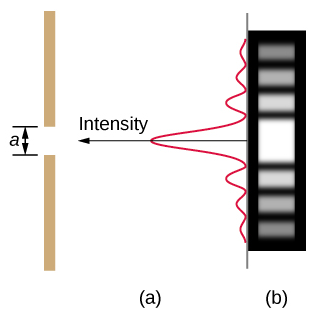
يوضح الشكل تحليل حيود الشق الواحد\(\PageIndex{2}\). هنا، يصل الضوء إلى الشق ويضيئه بشكل موحد ويكون في طور عرضه. ثم نفكر في انتشار الضوء من أجزاء مختلفة من نفس الشق. وفقًا لمبدأ Huygens، يصدر كل جزء من واجهة الموجة في الشق موجات، كما ناقشنا في The Nature of Light. هذه مثل الأشعة التي تبدأ في الطور وتتجه في جميع الاتجاهات. (كل شعاع عمودي على الموجة الأمامية للموجة.) بافتراض أن الشاشة بعيدة جدًا مقارنة بحجم الشق، فإن الأشعة المتجهة نحو وجهة مشتركة تكون متوازية تقريبًا. عندما تتحرك للأمام مباشرة، كما هو الحال في الجزء (أ) من الشكل، فإنها تظل في المرحلة، ونلاحظ الحد الأقصى المركزي. ومع ذلك، عندما تنتقل الأشعة بزاوية بالنسبة إلى الاتجاه الأصلي للشعاع، ينتقل كل شعاع مسافة مختلفة إلى موقع مشترك، ويمكن أن يصل داخل الطور أو خارجه. في الجزء (ب)، ينتقل الشعاع من الأسفل لمسافة طول موجي واحد أبعد من الشعاع من الأعلى. وهكذا، ينتقل شعاع من المركز مسافة /2 أقل من تلك الموجودة في الحافة السفلية للشق، ويخرج من الطور، ويتداخل بشكل مدمر. شعاع من فوق المركز قليلاً وآخر من أعلى قليلاً من الأسفل يلغي كل منهما الآخر أيضًا. في الواقع، يتداخل كل شعاع من الشق بشكل مدمر مع شعاع آخر. بمعنى آخر، يؤدي الإلغاء الثنائي لجميع الأشعة إلى حد أدنى مظلم من الشدة عند هذه الزاوية. من خلال التماثل، يحدث حد أدنى آخر في نفس الزاوية على يمين اتجاه السقوط (باتجاه الجزء السفلي من الشكل) للضوء.
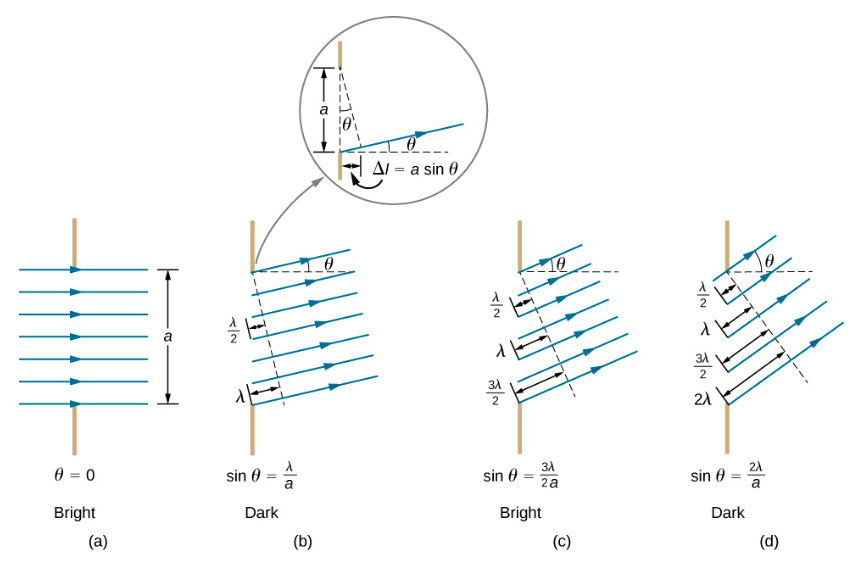
عند الزاوية الأكبر الموضحة في الجزء (ج)، تختلف أطوال\(3λ/2\) المسارات بمقدار أربعة أشعة من أعلى وأسفل الشق. ينتقل شعاع واحد مسافة\(λ\) مختلفة عن الشعاع من الأسفل ويصل في الطور، متداخلًا بشكل بناء. كما تضيف شعاعتان، كل منهما فوق هذين الشعاعين بقليل، بشكل بناء. تحتوي معظم الأشعة الصادرة من الشق على شعاع آخر للتدخل فيه بشكل بناء، وتحدث أقصى شدة عند هذه الزاوية. ومع ذلك، لا تتدخل جميع الأشعة بشكل بناء في هذا الموقف، وبالتالي فإن الحد الأقصى ليس بنفس كثافة الحد الأقصى المركزي. وأخيرًا، في الجزء (د)، تكون الزاوية الموضحة كبيرة بما يكفي لإنتاج الحد الأدنى الثاني. كما هو موضح في الشكل، يكون الفرق في طول مسار الأشعة من جانبي الشق هو\(a \sin \theta\)، ونرى أنه يتم الحصول على الحد الأدنى المدمر عندما تكون هذه المسافة مضاعفًا لا يتجزأ لطول الموجة.
وبالتالي، للحصول على تدخل مدمر لشق واحد،
\[\underbrace{a \sin θ = mλ}_{\text{destructive interference}} \nonumber \]
حيث
- \(m = ±1, ±2, ±3,...\)،
- \(a\)هو عرض الشق،
- \(λ\)هو الطول الموجي للضوء،
- \(θ\)هي الزاوية بالنسبة للاتجاه الأصلي للضوء، و
- \(m\)هو ترتيب الحد الأدنى.
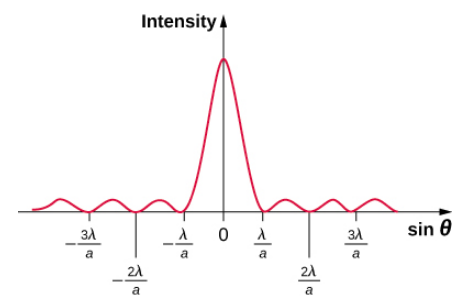
\(\PageIndex{3}\)يوضح الشكل رسمًا بيانيًا لشدة التداخل أحادي الشق، ومن الواضح أن الحد الأقصى على جانبي الحد الأقصى المركزي أقل كثافة بكثير وليس واسعًا. يتم استكشاف هذا التأثير في حيود الشق المزدوج.
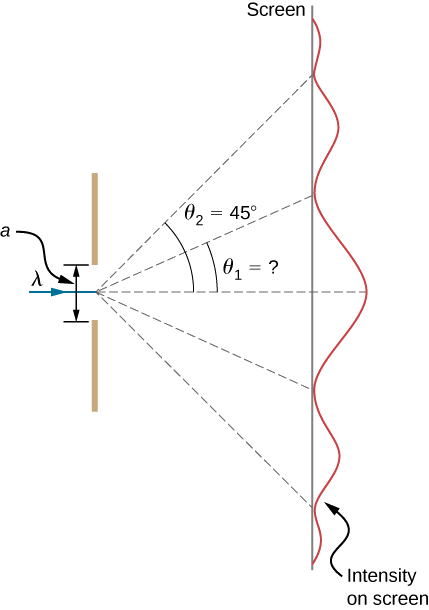
يسقط ضوء مرئي طوله الموجي ٥٥٠ نانومترًا على شق واحد وينتج الحد الأدنى من الحيود الثاني بزاوية ٤٥٫٠ درجة بالنسبة لاتجاه سقوط الضوء، كما في الشكل\(\PageIndex{5}\).
- ما عرض الشق؟
- ما الزاوية التي يُنتج بها الحد الأدنى الأول؟
إستراتيجية
من المعلومات المعطاة، وبافتراض أن الشاشة بعيدة عن الشق، يمكننا استخدام المعادلة\(a \sin θ = mλ\) أولاً لإيجاد زاوية الحد الأدنى الأول\(a\)، ومرة أخرى لإيجاد زاوية الحد الأدنى الأول\(\theta_1\).
الحل
- لقد حصلنا على ذلك\(λ=550\,nm\),\(m=2\), و\(\theta_2 = 45.0°\). يعطي حل المعادلة\(a \, \sin \, \theta = m\lambda\) للقيم\(a\) المعروفة واستبدالها
\[a = \frac{m\lambda}{\sin \, \theta_2} = \frac{2(550 \, nm)}{\sin \, 45.0°} = \frac{1100 \times 10^{-9} m}{0.707} = 1.56 \times 10^{-6} m. \nonumber \]
- يعطي\(a \, \sin \, \theta = m\lambda\) حل المعادلة\(\sin \, \theta_1\) واستبدال القيم المعروفة
\[\sin \, \theta_1 = \frac{m\lambda}{a} = \frac{1(550 \times 10^{-9}m)}{1.56 \times 10^{-6}m}. \nonumber \]
وبالتالي فإن الزاوية\(\theta_1\) هي\[\theta_1 = \sin^{-1}0.354 = 20.7°. \nonumber \]
الدلالة
نرى أن الشق ضيق (وهو أكبر ببضع مرات فقط من الطول الموجي للضوء). وهذا يتفق مع حقيقة أن الضوء يجب أن يتفاعل مع كائن مماثل في الحجم لطول الموجة من أجل إظهار تأثيرات موجية كبيرة مثل نمط الحيود أحادي الشق. نرى أيضًا أن الحد الأقصى المركزي يمتد 20.7 درجة على جانبي الشعاع الأصلي، بعرض حوالي 41 درجة. تبلغ الزاوية بين الحدين الأدنى الأول والثاني حوالي 24 درجة فقط (45.0 درجة −20.7 درجة). وبالتالي، فإن الحد الأقصى الثاني يبلغ حوالي نصف عرض الحد الأقصى المركزي.
لنفترض أن عرض الشق في المثال\(\PageIndex{1}\) قد زاد إلى\(1.8 \times 10^{-6} m\). ما المواضع الزاوية الجديدة للحدود الدنيا الأولى والثانية والثالثة؟ هل سيكون هناك حد أدنى رابع؟
- إجابة
-
\(17.8^o\)،\(37.7^o\)،\(66.4^o\)؛ لا


