3.6: مقياس ميكلسون للتداخل
- Page ID
- 196800
في نهاية هذا القسم، ستكون قادرًا على:
- اشرح التغيرات في الأطراف التي لوحظت باستخدام مقياس تداخل Michelson الناتجة عن حركات المرآة
- اشرح التغيرات في الأطراف التي لوحظت باستخدام مقياس تداخل Michelson الناتجة عن التغيرات في الوسط
يُعد مقياس تداخل Michelson (الذي ابتكره الفيزيائي الأمريكي ألبرت أ. ميشيلسون، 1852-1931) أداة دقيقة تنتج أطراف التداخل عن طريق تقسيم شعاع الضوء إلى جزأين ثم إعادة تجميعها بعد انتقالها في مسارات بصرية مختلفة. \(\PageIndex{1}\)يصور الشكل مقياس التداخل ومسار شعاع الضوء من نقطة واحدة على المصدر الممتد S، وهو عبارة عن لوحة زجاجية أرضية تنشر الضوء من مصباح أحادي اللون بطول موجة\(\lambda_0\). يصطدم الشعاع بالمرآة نصف الفضية M، حيث ينعكس نصفها على الجانب والنصف الآخر يمر عبر المرآة. ينتقل الضوء المنعكس إلى المرآة المستوية المتحركة\(M_1\)، حيث ينعكس مرة أخرى عبر M إلى الراصد. ينعكس النصف المرسل من الشعاع الأصلي مرة أخرى بواسطة المرآة الثابتة\(M_2\) ثم باتجاه الراصد بواسطة M.
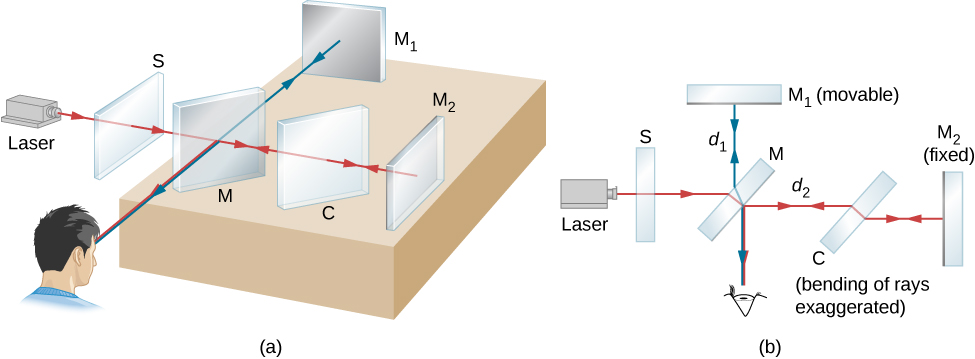
نظرًا لأن كلا الشعاعين ينبعان من نفس النقطة على المصدر، فإنهما متماثلان وبالتالي يتداخلان. لاحظ من الشكل أن شعاعًا واحدًا يمر عبر M ثلاث مرات والآخر مرة واحدة فقط. لضمان اجتياز كلا العوارض لنفس سماكة الزجاج، يتم وضع لوحة التعويض C من الزجاج الشفاف في الذراع المحتوي\(M_2\). هذه اللوحة هي نسخة مكررة من M (بدون الفضة) وعادة ما يتم قطعها من نفس قطعة الزجاج المستخدمة لإنتاج M. ومع وجود المعوض في مكانه، فإن أي فرق طوري بين الحزمتين يرجع فقط إلى الاختلاف في المسافات التي تقطعها.
فرق المسار بين الحزمتين عند إعادة دمجهما هو\(2d_1 - 2d_2\)، أين\(d_1\) المسافة بين M و\(M_1\)،\(d_2\) وهي المسافة بين M و\(M_2\). لنفترض أن فرق المسار هذا هو عدد صحيح من الأطوال الموجية\(m\lambda_0\). ثم يحدث التداخل البناء وتظهر صورة مشرقة للنقطة الموجودة على المصدر عند المراقب. الآن يخضع الضوء الصادر من أي نقطة أخرى على المصدر الذي يحتوي حزمه على نفس الاختلاف في المسار أيضًا لتداخل بنّاء وينتج صورة مشرقة. مجموعة صور النقاط هذه عبارة عن هامش ساطع يتوافق مع اختلاف المسار لـ\(m\lambda_0\) (الشكل\(\PageIndex{2}\)). عندما\(M_1\) يتم نقل مسافة\(\Delta d = \lambda_0/2\)، يتغير فرق المسار هذا بمقدار\(\lambda_0\)، ويتحرك كل طرف إلى الموضع الذي كان يشغله سابقًا طرف مجاور. وبالتالي، من خلال حساب عدد الأطراف m التي تمر بنقطة معينة أثناء\(M_1\) تحريكها، يمكن للمراقب قياس الإزاحة الدقيقة التي تكون دقيقة لجزء من الطول الموجي، كما هو موضح في العلاقة
\[\Delta d = m\dfrac{\lambda_0}{2}. \nonumber \]

يُستخدم ضوء ليزر أحمر طوله الموجي 630 nm في مقياس تداخل Michelson. مع الحفاظ على\(M_1\) ثبات المرآة،\(M_2\) يتم تحريك المرآة. وُجد أن الأطراف تتحرك متجاوزة الشعر المتقاطع الثابت في المشاهد. ابحث عن المسافة التي\(M_2\) يتم فيها تحريك المرآة لحافة واحدة لتجاوز الخط المرجعي.
إستراتيجية
راجع الشكل\(\PageIndex{1}\) لمعرفة الشكل الهندسي. نستخدم نتيجة حالة تداخل مقياس التداخل في Michelson للعثور على المسافة المقطوعة,\(Δd\).
الحل
بالنسبة لضوء الليزر الأحمر الذي يبلغ طوله 630 نانومتر، ولكل تقاطع هامشي (\(m = 1\))، فإن المسافة التي\(M_2\) تقطعها إذا بقيت\(M_1\) ثابتًا هي
\[\Delta d = m\dfrac{\lambda_0}{2} = 1 \times \dfrac{630 \, nm}{2} = 315 \, nm = 0.315 \, \mu m.\nonumber \]
الأهمية
أحد التطبيقات المهمة لهذا القياس هو تعريف العداد القياسي. كما هو مذكور في الوحدات والقياس، تم تعريف طول العداد القياسي مرة واحدة على أنه إزاحة المرآة في مقياس ميكلسون للتداخل المقابل لـ 1،650،763.73 أطوال موجية من الحافة المعينة من الكريبتون 86 في أنبوب تفريغ الغاز.
قياس معامل انكسار الغاز
في أحد أذرع مقياس تداخل Michelson، يتم وضع حجرة زجاجية مزودة بمرفقات لإخلاء الجزء الداخلي ووضع الغازات فيه. تبلغ المساحة داخل الحاوية 2 سم. في البداية، الحاوية فارغة. عندما يدخل الغاز ببطء إلى الغرفة، تلاحظ أن الأطراف المظلمة تتحرك عبر الخط المرجعي في مجال المراقبة. في الوقت الذي يتم فيه ملء الغرفة إلى الضغط المطلوب، تكون قد أحصيت 122 حافة تتحرك بعد الخط المرجعي. الطول الموجي للضوء المستخدم هو 632.8 nm. ما معامل الانكسار لهذا الغاز؟
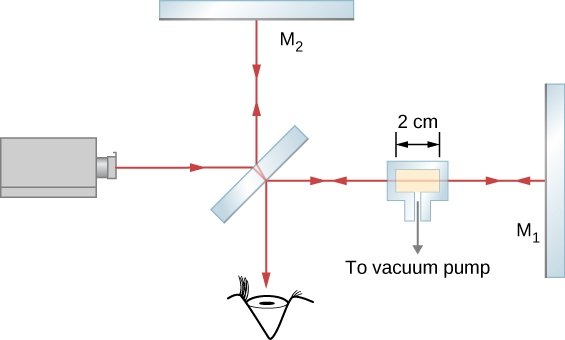
إستراتيجية
تشكل الأطراف m = 122 التي تمت ملاحظتها الفرق بين عدد الأطوال الموجية التي تتناسب مع الغرفة الفارغة (الفراغ) وعدد الأطوال الموجية التي تتناسب مع نفس الغرفة عندما تكون مملوءة بالغاز. يكون الطول الموجي في الغرفة الممتلئة أقصر بعامل n، وهو معامل الانكسار.
الحل
ينتقل الشعاع مسافة t = 2 سم إلى اليمين عبر الحجرة الزجاجية ومسافة أخرى t إلى اليسار عند الانعكاس. إجمالي السفر هو L = 2t. عندما تكون فارغة، يكون عدد الأطوال الموجية التي تناسب هذه الغرفة
\[N_0 = \dfrac{L}{\lambda_0} = \dfrac{2t}{\lambda_0} \nonumber \]
حيث\(\lambda_0 = 632.8\) nm هو الطول الموجي في فراغ الضوء المستخدم. في أي وسيط آخر، يكون\(\lambda = \lambda_0/n\) الطول الموجي وعدد الأطوال الموجية التي تتناسب مع الغرفة المملوءة بالغاز
\[N = \dfrac{L}{\lambda} = \dfrac{2t}{\lambda_0/n}. \nonumber \]
عدد الهوامش التي لوحظت في المرحلة الانتقالية هو
\[\begin{align*} m = N - N_0, \\[4pt] &= \dfrac{2t}{\lambda_0/n} - \dfrac{2t}{\lambda_0}, \\[4pt] &= \dfrac{2t}{\lambda_0}(n - 1). \end{align*} \nonumber \]
الحل لـ (n−1) يعطي
\[n - 1 = m \left(\dfrac{\lambda_0}{2t}\right) = 122 \left(\dfrac{632.8 \times 10^{-9}m}{2(2 \times 10^{-2}m)}\right) = 0.0019 \nonumber \]
و\(n = 1.0019\)
الأهمية
إن مؤشرات الانكسار للغازات قريبة جدًا من معامل الفراغ، لدرجة أننا نعتبرها عادةً مساوية لـ 1. الفرق بين 1 و 1.0019 صغير جدًا لدرجة أن قياسه يتطلب تقنية حساسة مماثلة مثل قياس التداخل. لا يمكننا، على سبيل المثال، أن نأمل في قياس هذه القيمة باستخدام تقنيات تستند ببساطة إلى قانون Snell.
على الرغم من أن m، وهو عدد الهوامش التي تمت ملاحظتها، هو عدد صحيح، والذي غالبًا ما يُنظر إليه على أنه لا يحتوي على أي شك، فمن الناحية العملية، من السهل جدًا فقدان المسار عند حساب الهوامش. على سبيل المثال\(\PageIndex{1}\)، إذا قدرت أنك ربما فقدت ما يصل إلى خمسة هوامش عند الإبلاغ عن\(m=122\) الهوامش، (أ) هل قيمة مؤشر الانكسار التي تم حسابها في المثال كبيرة\(\PageIndex{1}\) جدًا أم صغيرة جدًا؟ (ب) كم المبلغ؟
- إجابة
-
أ. صغير جدًا؛ ب. يصل إلى\(8 \times 10^{-5}\)
- الخطوة 1. افحص الموقف لتحديد التداخل. حدد ما إذا كانت الشقوق أو الأغشية الرقيقة أو مقاييس التداخل تؤخذ في الاعتبار في المشكلة.
- الخطوة 2. في حالة وجود شقوق، لاحظ أن حواجز الحيود والشقوق المزدوجة تنتج أنماط تداخل متشابهة جدًا، ولكن الحواجز الشبكية لها حدود قصوى أضيق (أكثر حدة). تتميز أنماط الشق الواحد بحد أقصى مركزي كبير وحد أقصى أصغر على الجانبين.
- الخطوة 3. في حالة تداخل الأغشية الرقيقة أو مقياس التداخل، لاحظ فرق طول المسار بين الشعاعين المتداخلين. تأكد من استخدام الطول الموجي في الوسيط المعني، لأنه يختلف عن الطول الموجي في الفراغ. لاحظ أيضًا أن هناك تحولًا إضافيًا في الطور /2/2 عندما ينعكس الضوء من وسط بمعامل انكسار أكبر.
- الخطوة 4. حدد بالضبط ما يجب تحديده في المشكلة (حدد المجهول). القائمة المكتوبة مفيدة. ارسم مخططًا للوضع. يعد وضع العلامات على الرسم التخطيطي مفيدًا.
- الخطوة 5. قم بعمل قائمة بما هو معطى أو يمكن استنتاجه من المشكلة كما هو مذكور (حدد المعروف).
- الخطوة 6. حل المعادلة المناسبة للكمية التي سيتم تحديدها (المجهول) وأدخل القيم المعروفة. تتضمن الشقوق وحواجز شبكية وحدود رايلي المعادلات.
- الخطوة 7. بالنسبة للتداخل في الأغشية الرقيقة، يكون لديك تداخل بنّاء للتحول الكلي الذي يمثل عددًا لا يتجزأ من الأطوال الموجية. لديك تداخل مدمر للتحول الكلي لعدد نصف متكامل من الأطوال الموجية. ضع في اعتبارك دائمًا أن الشعار إلى القمة بنّاء بينما من القمة إلى الحوض مدمرة.
- الخطوة 8. تحقق لمعرفة ما إذا كانت الإجابة معقولة: هل لها معنى؟ لا يمكن أن تكون الزوايا في أنماط التداخل أكبر من 90 درجة، على سبيل المثال.


