3.5: التداخل في الأغشية الرقيقة
- Page ID
- 196807
في نهاية هذا القسم، ستكون قادرًا على:
- وصف تغييرات المرحلة التي تحدث عند التفكير
- وصف الحواف التي تم إنشاؤها بواسطة الأشعة المنعكسة من مصدر مشترك
- شرح مظهر الألوان في الأفلام الرقيقة
تنتج الألوان الزاهية التي تظهر في بقعة الزيت العائمة على الماء أو في فقاعة الصابون المضاءة بنور الشمس عن التداخل. الألوان الأكثر سطوعًا هي تلك التي تتدخل بشكل بناء. يحدث هذا التداخل بين الضوء المنعكس من الأسطح المختلفة للغشاء الرقيق؛ وبالتالي، يُعرف التأثير بتداخل الأغشية الرقيقة.
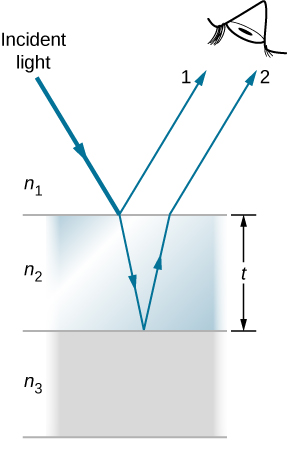
كما لاحظنا من قبل، تكون تأثيرات التداخل أكثر بروزًا عندما يتفاعل الضوء مع شيء له حجم مشابه لطول الموجة. الطبقة الرقيقة هي تلك التي يقل\(t\) سمكها عن بضعة أضعاف الطول الموجي للضوء\(λ\). نظرًا لأن اللون يرتبط بشكل غير مباشر\(λ\) ولأن كل التداخل يعتمد بطريقة ما على النسبة\(λ\) إلى حجم الكائن المعني، يجب أن نتوقع رؤية ألوان مختلفة لسماكات مختلفة للفيلم، كما في الشكل\(\PageIndex{1}\).

ما الذي يسبب تداخل الأغشية الرقيقة؟ \(\PageIndex{2}\)يوضح الشكل كيف يمكن للضوء المنعكس من السطوح العلوية والسفلية للفيلم أن يتداخل. ينعكس الضوء الساقط جزئيًا فقط من السطح العلوي للفيلم (الشعاع 1). يدخل الباقي الفيلم وينعكس جزئيًا من السطح السفلي. يمكن أن يخرج جزء من الضوء المنعكس من السطح السفلي من الجزء العلوي من الفيلم (الشعاع 2) ويتداخل مع الضوء المنعكس من الأعلى (الشعاع 1). ينتقل الشعاع الذي يدخل الفيلم مسافة أكبر، لذلك قد يكون داخل الطور أو خارجه مع انعكاس الشعاع من الأعلى. ومع ذلك، فكر للحظة، مرة أخرى، في الفقاعات الموجودة في الشكل\(\PageIndex{1}\). تكون الفقاعات أكثر ظلامًا في الأماكن التي تكون فيها أنحف. علاوة على ذلك، إذا لاحظت فقاعة الصابون بعناية، ستلاحظ أنها تصبح مظلمة عند النقطة التي تنكسر فيها. بالنسبة للأفلام الرقيقة جدًا، يكون الفرق في أطوال مسارات الأشعة 1 و 2 في الشكل\(\PageIndex{2}\) ضئيلًا، فلماذا يجب أن تتداخل بشكل مدمر وليس بشكل بناء؟ الإجابة هي أن تغيير المرحلة يمكن أن يحدث عند التفكير، كما هو موضح لاحقًا.
التغييرات في المرحلة بسبب الانعكاس
لقد رأينا سابقًا (الموجات) أن انعكاس الموجات الميكانيكية يمكن أن يتضمن تغييرًا في الطور بمقدار 180 درجة. على سبيل المثال، يتم عكس الموجة المتحركة على الخيط (أي تغيير الطور بمقدار 180 درجة) عند الانعكاس عند الحد الذي يرتبط به خيط أثقل. ومع ذلك، إذا كانت السلسلة الثانية أخف (أو بشكل أكثر دقة، ذات كثافة خطية أقل)، فلن يحدث أي انعكاس. تنتج موجات الضوء نفس التأثير، لكن المعلمة الحاسمة للضوء هي معامل الانكسار. تخضع الموجات الضوئية لتغير طور 180 درجة أو\(\pi\) راديان عند الانعكاس على واجهة يكون بعدها متوسط معامل الانكسار العالي. لا يحدث أي تغيير في الطور عند الانعكاس من وسط معامل انكسار منخفض (الشكل\(\PageIndex{3}\)). نظرًا للطبيعة الدورية للموجات، فإن تغيير الطور أو الانعكاس هذا يعادل\(±λ/2\) المسافة المقطوعة أو طول المسار. يعد كل من طول المسار ومؤشرات الانكسار من العوامل المهمة في تداخل الأغشية الرقيقة.
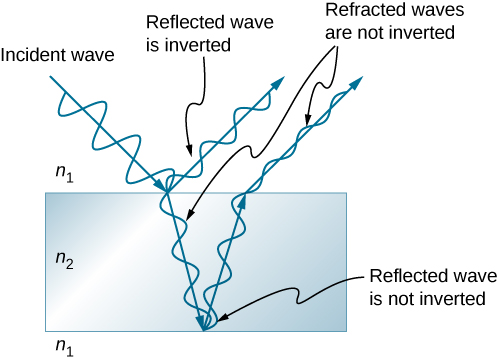
إذا كان الفيلم في الشكل\(\PageIndex{3}\) عبارة عن فقاعة صابون (في الأساس ماء بهواء على كلا الجانبين)،\(λ/2\) فسيحدث تحول طوري في الشعاع 1 وليس للشعاع 2. وبالتالي، عندما يكون الفيلم رقيقًا جدًا ويكون فرق طول المسار بين الشعاعين ضئيلًا، فإنهما خارج الطور تمامًا، ويحدث التداخل المدمر في جميع الأطوال الموجية. وبالتالي، فإن فقاعة الصابون مظلمة هنا. يعتبر سمك الفيلم بالنسبة لطول موجة الضوء هو العامل الحاسم الآخر في تداخل الأغشية الرقيقة. \(\PageIndex{3}\)ينتقل الشعاع 2 في الشكل لمسافة أكبر من الشعاع 1. بالنسبة للضوء الساقط عموديًا على السطح، ينتقل الشعاع 2 مسافة\(2t\) أبعد تقريبًا من الشعاع 1. عندما تكون هذه المسافة مضاعفًا تكامليًا أو نصف تكامليًا لطول الموجة في الوسط (\(\lambda_n = \lambda/n\)، حيث هو الطول الموجي في الفراغ\(n\) وهو مؤشر الانكسار)، يحدث التداخل البنائي أو المدمر، اعتمادًا أيضًا على ما إذا كان هناك تغيير طوري في أي من الشعاعين.
تستخدم الكاميرات المتطورة سلسلة من العدسات المتعددة. يمكن للضوء أن ينعكس من أسطح هذه العدسات المختلفة ويقلل من وضوح الصورة. للحد من هذه الانعكاسات، يتم طلاء العدسات بطبقة رقيقة من فلوريد المغنيسيوم، مما يسبب تداخلًا مدمرًا للغشاء الرقيق. ما أنحف مقدار يمكن أن يكون عليه هذا الفيلم، إذا كان معامل انكساره هو ١٫٣٨ ومُصمَمًا للحد من انعكاس ضوء ٥٥٠ نانومترًا، وهو عادةً ما يكون الطول الموجي المرئي الأكثر كثافة؟ افترض أن معامل انكسار الزجاج هو 1.52.
إستراتيجية
راجع الشكل\(\PageIndex{2}\)\(n_1 = 1.00\) واستخدمه للهواء و\(n_2 = 1.38\) و\(n_3 = 1.52\). كل من الشعاع 1 والشعاع 2 لهما تحول /2 عند الانعكاس. وبالتالي، للحصول على تداخل مدمر، يحتاج الشعاع 2 إلى الانتقال بنصف طول موجة أبعد من الشعاع 1. بالنسبة للأشعة المتساقطة بشكل عمودي، يكون فرق طول المسار هو 2 طن.
الحل
للحصول على تدخل مدمر هنا،
\[2t = \dfrac{\lambda_{n2}}{2} \nonumber \]
\(\lambda_{n2}\)أين الطول الموجي في الفيلم ويتم إعطاؤه بواسطة\(\lambda_{n2} = \lambda / n_2\). وهكذا،
\[2t = \dfrac{\lambda/n_2}{2}. \nonumber \]
حل العائد من t وإدخال القيم المعروفة
\[t = \dfrac{\lambda/n_2}{4} = \dfrac{(500 \, nm)/1.38}{4} = 99.6 \, nm. \nonumber \]
الدلالة
تعتبر الأفلام مثل تلك الموجودة في هذا المثال أكثر فاعلية في إنتاج التداخل المدمر عند استخدام الطبقة الأقل سمكًا، حيث تقل شدة الضوء فوق نطاق أوسع من زوايا السقوط. هذه الأفلام تسمى الطلاءات غير العاكسة؛ ولكن هذا مجرد وصف صحيح تقريبًا، نظرًا لأن الأطوال الموجية الأخرى يتم إلغاؤها جزئيًا فقط. تستخدم الطلاءات غير العاكسة أيضًا في نوافذ السيارات والنظارات الشمسية.
الجمع بين فرق طول المسار وتغيير الطور
يكون تداخل الأغشية الرقيقة أكثر فائدة أو أكثر تدميرًا عندما يكون فرق طول المسار للشعاعين هو طول موجة متكامل أو نصف متكامل. وهذا يعني، بالنسبة للأشعة المتساقطة بشكل عمودي،
\[2t = \lambda_n, \, 2\lambda_n, \, 3\lambda_n, ... \, or \, 2t = \lambda_n/2, \, 3\lambda_n/2, \, 5\lambda_n/2, ... \nonumber \]
لمعرفة ما إذا كان التداخل بناءً أم مدمرًا، يجب عليك أيضًا تحديد ما إذا كان هناك تغيير في المرحلة عند التفكير. وبالتالي يعتمد تداخل الأغشية الرقيقة على سمك الفيلم والطول الموجي للضوء ومؤشرات الانكسار. بالنسبة للضوء الأبيض الساقط على فيلم يختلف سمكه، يمكنك ملاحظة ألوان قوس قزح للتداخل البنّاء لأطوال موجية مختلفة مع اختلاف السماكة.
- ما أصغر ثلاث سماكات لفقاعة الصابون التي تُحدث تداخلًا تركيبيًا للضوء الأحمر بطول موجة ٦٥٠ نانومترًا؟ يعتبر معامل انكسار الصابون هو نفس معامل انكسار الماء.
- ما أصغر ثلاث سماكات تُحدث تداخلًا مدمرًا؟
إستراتيجية
استخدم الشكل\(\PageIndex{3}\) لتصور الفقاعة، التي تعمل كطبقة رقيقة بين طبقتين من الهواء. وهكذا\(n_1 = n_3 = 1.00\) للهواء والصابون (أي ما يعادل الماء).\(n_2 = 1.333\) هناك تحول /2 للشعاع 1 ينعكس من السطح العلوي للفقاعة ولا يوجد تحول للشعاع 2 المنعكس من السطح السفلي. للحصول على تداخل بنّاء، إذن، يجب أن يكون فرق طول المسار (2 t) مضاعفًا نصفيًا للطول الموجي - الثلاثة الأولى هي\(\lambda_n/2, \, 3\lambda_n/2\)، و\(5\lambda_n/2\). للحصول على تداخل مدمر، يجب أن يكون فرق طول المسار مضاعفًا لا يتجزأ للطول الموجي - الثلاثة الأولى هي 0، و\(\lambda_n\)، و\(2\lambda_n\).
الحل
أ. يحدث التداخل البنائي هنا عندما
\[2t_c = \dfrac{\lambda_n}{2}, \, \dfrac{3\lambda_n}{2}, \, \dfrac{5\lambda_n}{2}, ... \nonumber \]
وبالتالي، فإن أصغر سماكة بناءة\(t_c\) هي
\[t_c = \dfrac{\lambda_n}{4} = \dfrac{\lambda/n}{4} = \dfrac{(650 \, nm)/1.333}{4} = 122 \, nm. \nonumber \]
السماكة التالية التي تعطي تداخلًا بناءً هي\(t'_c = 3\lambda_n/4\)، لذلك
\[t'_c = 366 \, nm. \nonumber \]
أخيرًا، السماكة الثالثة التي تنتج التداخل البناء هي\(t'_c = 5\lambda_n/4\)، لذلك
\[t'_c = 610 \, nm. \nonumber \]
ب- بالنسبة للتداخل المدمر، يكون فرق طول المسار هنا مضاعفًا لا يتجزأ للطول الموجي. يحدث الأول للسمك الصفري، نظرًا لوجود تغيير طوري في السطح العلوي، أي
\[t_d = 0, \nonumber \]
الحالة الرقيقة جدًا (أو الرقيقة جدًا) التي تمت مناقشتها أعلاه. أول سمك غير صفري ينتج تداخلًا مدمرًا هو
\[2t'_d = \lambda_n. \nonumber \]
يعطي استبدال القيم المعروفة
\[t'_d = \dfrac{\lambda}{2} = \dfrac{\lambda/n}{2} = \dfrac{(650 \, nm)/1.333}{2} = 244 \, nm. \nonumber \]
أخيرًا، السماكة المدمرة الثالثة هي\(2t''_d = 2\lambda_n\)، لذلك
\[t''_d = \lambda_n = \dfrac{\lambda}{n} = \dfrac{650 \, nm}{1.333} = 488 \, nm. \nonumber \]
الدلالة
إذا كانت الفقاعة مضاءة بضوء أحمر نقي، فسوف نرى شرائط مشرقة ومظلمة بزيادات موحدة جدًا في السماكة. سيكون أولاً شريطًا داكنًا بسماكة 0، ثم ساطعًا بسماكة 122 نانومتر، ثم داكنًا عند 244 نانومتر، ومشرقًا عند 366 نانومتر، وداكنًا عند 488 نانومتر، ومشرقًا عند 610 نانومتر. إذا اختلفت سماكة الفقاعة بسلاسة، مثل الإسفين الناعم، فستكون الأربطة متباعدة بشكل متساوٍ.
للمضي قدمًا مع المثال\(\PageIndex{2}\)، ما هي السماكتان التاليان لفقاعة الصابون التي من شأنها أن تؤدي إلى
- التدخل البناء، و
- تدخل مدمر؟
- الإجابة أ
-
853 نانومتر و 1097 نانومتر
- الإجابة ب
-
731 نانومتر و 975 نانومتر
يمكن رؤية مثال آخر لتداخل الأغشية الرقيقة عند فصل شرائح المجهر (انظر الشكل\(\PageIndex{4}\)). الشرائح مسطحة جدًا، بحيث يزداد سمك إسفين الهواء بينهما بشكل موحد جدًا. يحدث تغيير الطور عند السطح الثاني ولكن ليس الأول، لذلك يتشكل شريط داكن حيث تتلامس الشرائح. تتكرر ألوان قوس قزح للتداخل البنّاء، حيث تنتقل من البنفسجي إلى الأحمر مرارًا وتكرارًا مع زيادة المسافة بين الشرائح. مع زيادة طبقة الهواء، تصبح رؤية النطاقات أكثر صعوبة، لأن التغييرات الطفيفة في زاوية السقوط لها تأثيرات أكبر على اختلافات طول المسار. في حالة استخدام ضوء أحادي اللون بدلاً من الضوء الأبيض، يتم الحصول على أشرطة ساطعة ومظلمة بدلاً من تكرار ألوان قوس قزح.
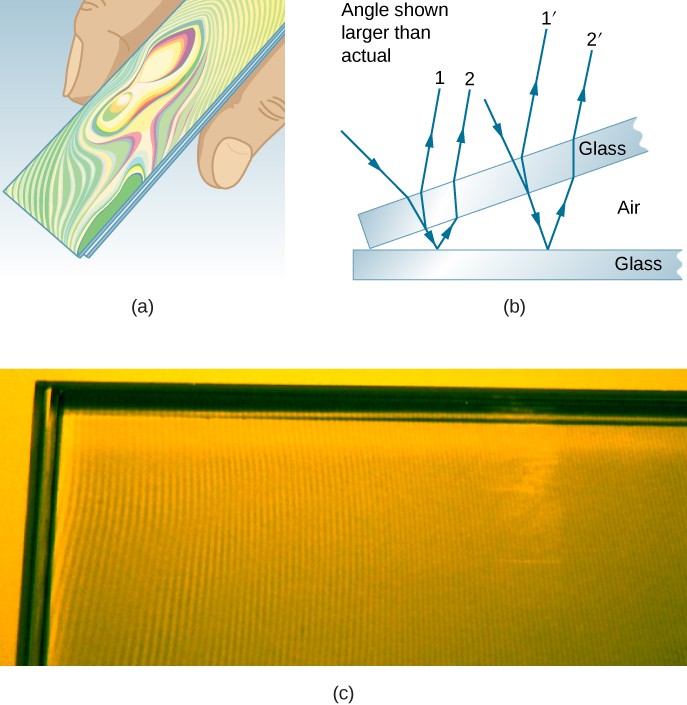
يوجد تطبيق مهم لتداخل الأغشية الرقيقة في تصنيع الأدوات البصرية. يمكن مقارنة العدسة أو المرآة بالعدسة الرئيسية أثناء تأريضها، مما يسمح بتشكيلها بدقة أقل من الطول الموجي على سطحها بالكامل. \(\PageIndex{5}\)يوضح الشكل ظاهرة تسمى حلقات نيوتن، والتي تحدث عندما يتم وضع السطوح المستوية للعدستين معًا. (تُسمى النطاقات الدائرية بحلقات نيوتن لأن إسحاق نيوتن وصفها واستخدامها بالتفصيل. لم يكتشفها نيوتن؛ روبرت هوك اكتشفها، ولم يعتقد نيوتن أنها كانت بسبب الطابع الموجي للضوء.) تشير كل حلقة متتالية من لون معين إلى زيادة بمقدار نصف طول موجة فقط في المسافة بين العدسة والفراغ، بحيث يمكن الحصول على دقة عالية. بمجرد أن تصبح العدسة مثالية، لا تظهر أي حلقات.

للتداخل بين الأغشية الرقيقة العديد من التطبيقات الأخرى، سواء في الطبيعة أو في التصنيع. تتميز أجنحة بعض الفراشات والفراشات بألوان قزحية تقريبًا بسبب تداخل الأغشية الرقيقة. بالإضافة إلى التصبغ، يتأثر لون الجناح بشكل كبير بالتداخل البناء لأطوال موجية معينة تنعكس من سطحه المطلي بالفيلم. تقدم بعض شركات تصنيع السيارات وظائف طلاء خاصة تستخدم تداخل الأغشية الرقيقة لإنتاج ألوان تتغير مع الزاوية. يعتمد هذا الخيار المكلف على تباين اختلافات طول مسار الأغشية الرقيقة مع الزاوية. تستخدم ميزات الأمان الموجودة على بطاقات الائتمان والأوراق النقدية ورخص القيادة والأشياء المماثلة المعرضة للتزوير تداخل الأغشية الرقيقة أو حواجز الحيود أو الصور المجسمة. في وقت مبكر من عام 1998، احتلت أستراليا الصدارة في إصدار فواتير الدولار المطبوعة على البوليمر مع ميزة أمان محزوز الحيود، مما يجعل من الصعب تزوير العملة. تستخدم دول أخرى، مثل كندا ونيوزيلندا وتايوان، تقنيات مماثلة، بينما تتضمن العملة الأمريكية تأثير تداخل الأغشية الرقيقة.


