3.4: تداخل متعدد الشقوق
- Page ID
- 196799
في نهاية هذا القسم، ستكون قادرًا على:
- وصف مواقع وشدة الحدود القصوى الثانوية للتداخل متعدد الشقوق
يحدد تحليل تداخل الضوء الذي يمر عبر شقين الإطار النظري للتداخل ويعطينا نظرة تاريخية عن تجارب توماس يونغ. ومع ذلك، فإن الكثير من التطبيقات الحديثة لتداخل الشق لا تستخدم فقط شقين ولكن العديد منها يقترب من اللانهاية لأغراض عملية. يُطلق على العنصر البصري الرئيسي اسم محزوز الحيود، وهو أداة مهمة في التحليل البصري، ونناقشه بالتفصيل في الفصل الخاص بالانحراف. هنا، نبدأ تحليل التداخل متعدد الشقوق من خلال أخذ النتائج من تحليلنا للشق المزدوج (N = 2) وتوسيعه إلى التكوينات التي تحتوي على ثلاثة وأربعة وأعداد أكبر بكثير من الشقوق.
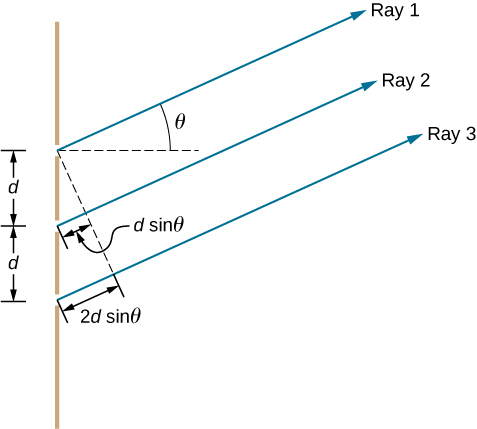
\(\PageIndex{1}\)يوضح الشكل أبسط حالة للتداخل متعدد الشقوق، باستخدام ثلاث فتحات، أو N = 3. المسافة بين الشقوق هي d، وفرق طول المسار بين الشقوق المتجاورة هو d sin، مثل حالة الشق المزدوج. الجديد هو أن فرق طول المسار للشقين الأول والثالث هو 2d sin. شرط التداخل البناء هو نفسه بالنسبة للشق المزدوج، أي
\[d \sin θ=mλ \nonumber \]
عند استيفاء هذا الشرط، يصبح الرقم 2d sin تلقائيًا مضاعفًا لـ، لذلك تتحد الأشعة الثلاثة بشكل بناء، وتسمى الأطراف الساطعة التي تحدث هنا باسم الحد الأقصى الرئيسي. ولكن ماذا يحدث عندما يكون فرق طول المسار بين الشقوق المتجاورة /2 فقط؟ يمكننا التفكير في الأشعة الأولى والثانية على أنها تتدخل بشكل مدمر، لكن الشعاع الثالث يبقى دون تغيير. بدلاً من الحصول على حافة داكنة، أو الحد الأدنى، كما فعلنا للشق المزدوج، نرى حدًا أقصى ثانويًا بكثافة أقل من الحد الأقصى الرئيسي.
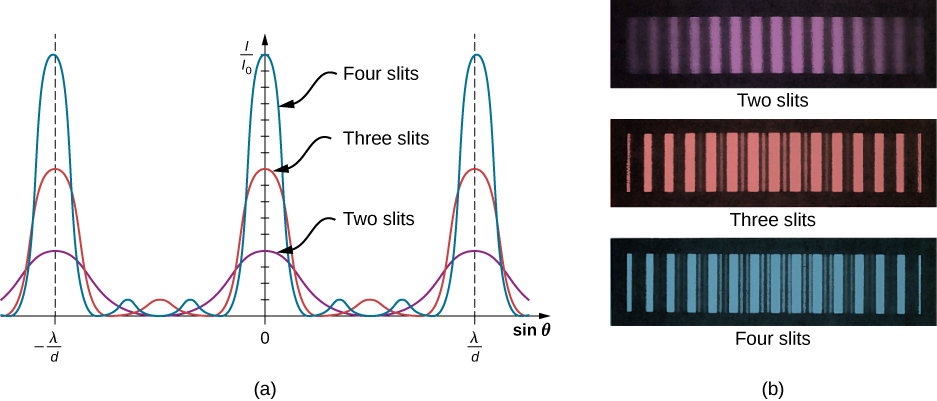
بشكل عام، بالنسبة للشقوق N، تحدث هذه الحدود القصوى الثانوية عند وجود شعاع غير مزاوج لا يزول بسبب التداخل المدمر. يحدث هذا في المواضع (N−2) المتباعدة بالتساوي بين الحد الأقصى الرئيسي. وفي المقابل، تقل سعة الموجة الكهرومغناطيسية إلى 1/N من الموجة عند الحد الأقصى الرئيسي، وتتناقص شدة الضوء، التي تتناسب مع مربع سعة الموجة، إلى\(1/N^2\) الكثافة مقارنة بالحد الأقصى الرئيسي. كأنماط\(\PageIndex{2}\) تداخل في الشكل تتكون من شقين وثلاثة وأربعة شقوق. مع زيادة عدد الشقوق، يظهر المزيد من الحدود القصوى الثانوية، لكن الحد الأقصى الرئيسي يظهر أن الحافة الداكنة تقع بين كل حد أقصى (أساسي أو ثانوي). مع نمو N بشكل أكبر وزيادة عدد الأطراف الساطعة والمظلمة، يصبح عرض الحد الأقصى أضيق بسبب الحواف الداكنة المجاورة القريبة. نظرًا لأن الكمية الإجمالية للطاقة الضوئية تظل دون تغيير، تتطلب الحدود القصوى الضيقة أن يصل كل حد أقصى إلى كثافة أعلى مماثلة.