Skip to main content
Global

1.7: مبدأ هيغنز

  1. Last updated
  2. Save as PDF
  • Page ID
    196660

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • وصف مبدأ هيغنز
    • استخدم مبدأ Huygens لشرح قانون التفكير
    • استخدم مبدأ Huygens لشرح قانون الانكسار
    • استخدم مبدأ Huggens لشرح الانحراف

    حتى الآن في هذا الفصل، ناقشنا الظواهر البصرية باستخدام نموذج أشعة الضوء. ومع ذلك، تتطلب بعض الظواهر التحليل والتفسيرات بناءً على خصائص موجة الضوء. هذا صحيح بشكل خاص عندما لا يكون الطول الموجي ضئيلًا مقارنة بأبعاد الجهاز البصري، مثل الشق في حالة الحيود. مبدأ Huygens هو أداة لا غنى عنها لهذا التحليل.

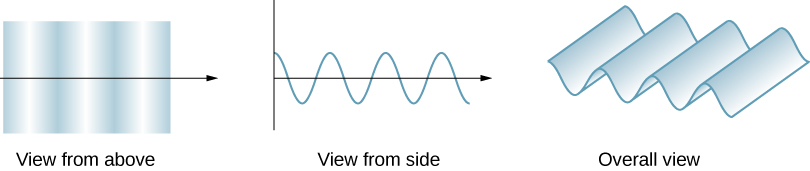
    \(\PageIndex{1}\)يوضح الشكل كيف تبدو الموجة العرضية كما تظهر من الأعلى ومن الجانب. يمكن تخيل موجة ضوئية تنتشر بهذه الطريقة، على الرغم من أننا لا نراها في الواقع تتأرجح عبر الفضاء. من الأعلى، ننظر إلى جبهات الأمواج (أو قمم الأمواج) كما لو كنا ننظر إلى أسفل على أمواج المحيط. سيكون المنظر الجانبي عبارة عن رسم بياني للمجال الكهربائي أو المغناطيسي. ربما تكون وجهة النظر من الأعلى أكثر فائدة في تطوير مفاهيم حول البصريات الموجية.

    تحتوي الأشكال الثلاثة على ثلاثة مشاهد للموجة. الأول هو وجهة نظر من الأعلى. تنتشر الموجة إلى اليمين، وتظهر كسلسلة من الشرائط الرأسية التي تتناوب تدريجيًا من الظلام إلى الضوء وتتكرر. العرض التالي هو منظر من الجانب. تنتشر الموجة مرة أخرى إلى اليمين وتظهر كمنحنى جيبي يتذبذب فوق وأسفل سهم أسود يشير إلى اليمين الذي يعمل كمحور أفقي. والثالث هو نظرة عامة. هذه صورة منظورية لموجة بنفس الطول الموجي كما في الصورتين الأوليين وتبدو وكأنها سطح متموج..
    الشكل\(\PageIndex{1}\): موجة عرضية، مثل موجة الضوء الكهرومغناطيسي، كما يُنظر إليها من الأعلى ومن الجانب. يكون اتجاه الانتشار عموديًا على جبهات الموجة (أو قمم الموجة) ويتم تمثيله بواسطة شعاع.

    طور العالم الهولندي كريستيان هويغنز (1629-1695) أسلوبًا مفيدًا لتحديد كيفية ومكان انتشار الأمواج بالتفصيل. بدءًا من بعض المواقع المعروفة، ينص مبدأ Huygens على أن كل نقطة على جبهة الموجة هي مصدر للموجات التي تنتشر في الاتجاه الأمامي بنفس سرعة الموجة نفسها. واجهة الموجة الجديدة ممامسة لجميع الموجات.

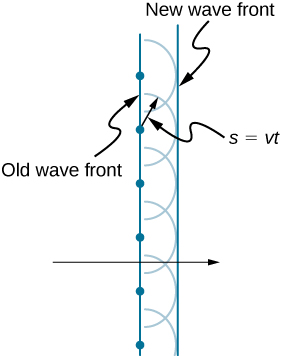
    \(\PageIndex{2}\)يوضح الشكل كيفية تطبيق مبدأ Huygens. واجهة الموجة هي الحافة الطويلة التي تتحرك، على سبيل المثال، مع القمة أو الحوض الصغير. تصدر كل نقطة على واجهة الموجة موجة نصف دائرية تتحرك بسرعة الانتشار\(v\). يمكننا رسم هذه الموجات في وقت\(t\) لاحق، بحيث تتحرك مسافة\(s=vt\). واجهة الموجة الجديدة عبارة عن مماس مستوٍ للموجات وهي المكان الذي نتوقع أن تكون فيه الموجة في وقت\(t\) لاحق. يعمل مبدأ Huygens على جميع أنواع الموجات، بما في ذلك موجات الماء والموجات الصوتية وموجات الضوء. إنه مفيد ليس فقط في وصف كيفية انتشار موجات الضوء ولكن أيضًا في شرح قوانين الانعكاس والانكسار. بالإضافة إلى ذلك، سنرى أن مبدأ Huygens يخبرنا كيف وأين تتداخل أشعة الضوء.

    يوضح هذا الشكل خطين رأسيين مستقيمين، مع تسمية الخط الأيسر باسم الموجة القديمة الأمامية والخط الأيمن باسم جبهة الموجة الجديدة. في منتصف الصورة، يعبر سهم أسود أفقي كلا الخطين ويشير إلى اليمين. يمر الخط الأمامي للموجة القديمة عبر ست نقاط متباعدة بشكل متساوٍ، بأربع نقاط فوق السهم الأسود وأربع نقاط أسفل السهم الأسود. تعمل كل نقطة كمركز لنصف دائرة مقابلة، وجميع دوائر نصف الدائرة الثمانية لها نفس الحجم. أما واجهة الموجة الجديدة فهي ممامسة للحافة اليمنى من نصف الدائرة. تحتوي إحدى النقاط المركزية على سهم شعاعي يشير إلى نقطة في نصف الدائرة المقابلة. يتم تصنيف هذا السهم الشعاعي بأنه يساوي v t.
    الشكل\(\PageIndex{2}\): تم تطبيق مبدأ Huygens على جبهة الموجة المستقيمة. تصدر كل نقطة على واجهة الموجة موجة نصف دائرية تتحرك لمسافة s=vt. جبهة الموجة الجديدة هي خط مماس للموجات.

    انعكاس

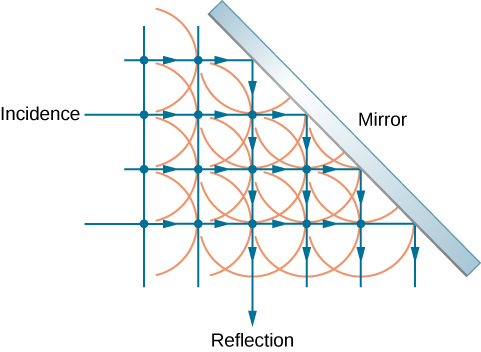
    \(\PageIndex{3}\)يوضح الشكل كيف تعكس المرآة الموجة الواردة بزاوية تساوي زاوية السقوط، مع التحقق من قانون الانعكاس. عندما تصطدم الموجة الأمامية بالمرآة، تنبعث الموجات أولاً من الجزء الأيسر من المرآة ثم من اليمين. كان لدى الموجات الأقرب إلى اليسار الوقت الكافي للانتقال لمسافة أبعد، مما أدى إلى ظهور جبهة موجية تتحرك في الاتجاه الموضح.

    يوضِّح الشكل شبكة من أربعة أشعة أفقية ومتوازية ومتساوية المسافات تسقط على مرآة مائلة بزاوية خمس وأربعين درجة أمام الأشعة. تنعكس الأشعة لأسفل من المرآة. تم تضمين شعاعين منعكسين إضافيين من الأشعة الساقطة فوق تلك الموضحة في الشكل. يتم رسم النقاط عند تقاطعات الأشعة الساقطة والمنعكسة. تتمركز نصف الدوائر التي تواجه اليمين والتي تمثل الموجات الساقطة ونصف الدائرة التي تتجه لأسفل لعكس الموجات على النقاط.
    الشكل\(\PageIndex{3}\): تم تطبيق مبدأ Huygens على واجهة الموجة الطائرة التي تضرب المرآة. انبعثت الموجات الموضحة عندما اصطدمت كل نقطة على واجهة الموجة بالمرآة. يُظهر المماس لهذه الموجات أن واجهة الموجة الجديدة قد انعكست بزاوية تساوي زاوية السقوط. يكون اتجاه الانتشار عموديًا على واجهة الموجة، كما هو موضح في الأسهم التي تشير إلى الأسفل.

    الانكسار

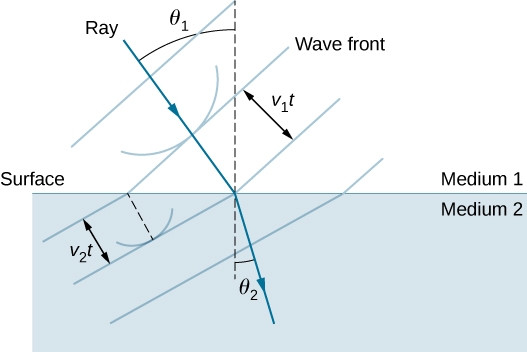
    يمكن تفسير قانون الانكسار من خلال تطبيق مبدأ Huygens على جبهة موجية تمر من وسط إلى آخر (الشكل\(\PageIndex{4}\)). كانت كل موجة في الشكل تنبعث عندما عبرت واجهة الموجة الواجهة بين الوسائط. نظرًا لأن سرعة الضوء أصغر في الوسط الثاني، فإن الموجات لا تنتقل بعيدًا في وقت معين، وتغير جبهة الموجة الجديدة اتجاهها كما هو موضح. وهذا يفسر سبب تغيير الشعاع لاتجاهه ليصبح أقرب إلى العمودي عندما يتباطأ الضوء. يمكن اشتقاق قانون Snell من الهندسة في الشكل\(\PageIndex{5}\) (مثال\(\PageIndex{1}\)).

    يعرض الشكل وسيلتين يفصل بينهما خط أفقي يسمى السطح. يُطلق على الوسيط العلوي اسم المتوسط الأول والوسيط السفلي يسمى المتوسط الثاني. في الصورة المتوسطة، يسقط شعاع على السطح وينتقل إلى الأسفل وإلى اليمين. يتم رسم خط منقط عمودي، عمودي على السطح، من خلال كلتا الوسيلتين حيث يصطدم الشعاع بالسطح. ينحني الشعاع المنكسر نحو هذا الخط المنقط حيث يدخل الوسط الثاني. يصنع مسار الشعاع زاوية ثيتا الفرعية الأولى مع الخط المنقط في الوسط الأول والزاوية ثيتا الفرعية الثانية مع الخط المنقط في الوسط الثاني، حيث يكون ثيتا الفرعية الثانية أقل من ثيتا الفرعية. تُرسم المقاطع الخطية، المُصنَّفة باسم الموجة الأمامية، بشكل عمودي على الشعاع الساقط والشعاع المنكسر. تكون مقاطع الخط هذه متباعدة بشكل متساوٍ داخل كل وسيط، لكن مقاطع الأسطر الثلاثة في الوسط 1 تكون متباعدة بشكل أوسع من مقاطع الخطوط الثلاثة في الوسط 2. يُطلق على الفصل بين مقاطع الخط هذه في الوسط 1 اسم v sub one t والفصل في الوسط 2 يسمى v sub two t، مع كون v sub two t أقل من v suber one t.
    الشكل\(\PageIndex{4}\): تم تطبيق مبدأ Huygens على جبهة الموجة الطائرة التي تنتقل من وسط إلى آخر، حيث تكون سرعتها أقل. ينحني الشعاع باتجاه العمودي، نظرًا لأن الموجات لها سرعة أقل في الوسط الثاني.

    مثال\(\PageIndex{1}\): اشتقاق قانون الانكسار

    من خلال فحص هندسة جبهات الموجة، اشتقاق قانون الانكسار.

    إستراتيجية

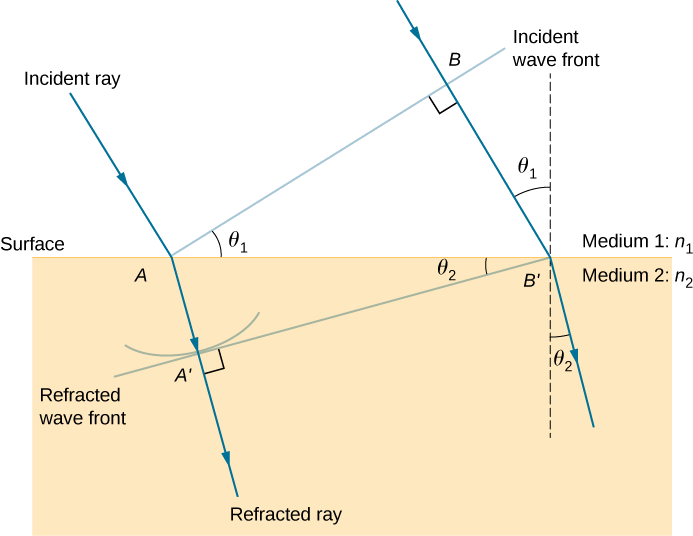
    ضع في اعتبارك الشكل\(\PageIndex{5}\) الذي يتوسع في الشكل \(\PageIndex{4}\). يُظهر واجهة الموجة الساقطة التي وصلت للتو إلى السطح عند النقطة A، بينما لا تزال النقطة B ضمن الوسط 1. في الوقت الذي\(Δt\) يستغرقه الطول الموجي للوصول \(B\)\(B'\) إلى السطح بسرعة\(v_1=c/n_1\)،\(A\) ينتقل الطول الموجي من إلى المتوسط 2 على مسافة من \(AA'=v_2Δt\)، أين\(v_2=c/n_2\). لاحظ أنه في هذا المثال، \(v_2\) أبطأ من\(v_1\) السبب\(n_1<n_2\).

    يوضح هذا الشكل هندسة انكسار الأشعة وجبهات الموجات. يوجد سطح أفقي بين المتوسط 1، بمعامل الانكسار n 1، والمتوسط 2، بمعامل الانكسار n 2. يظهر شعاع ساقط قادمًا من المتوسط 1 إلى المتوسط 2. يصطدم بالسطح عند النقطة A وينكسر باتجاه العادي في الوسط 2. يُرسم خط، يُطلق عليه اسم الموجة الساقطة الأمامية، من النقطة A الممتد بعيدًا عن السطح، عموديًا على الشعاع الساقط. الزاوية بين واجهة الموجة الساقطة والسطح هي ثيتا 1. يتم رسم الشعاع الساقط الثاني بالتوازي مع الشعاع الأول. يتقاطع هذا الشعاع مع مقدمة الموجة الساقطة عند نقطة تسمى B ويصطدم بالسطح عند نقطة تسمى B prime. يتم رسم خط متقطع عموديًا على السطح عند B prime. الزاوية بين هذا الخط العمودي والشعاع الثاني تساوي أيضًا ثيتا واحدة. المثلث المكوَّن من A وB وB Prime هو مثلث قائم الزاوية ثيتا واحدة عند A والزاوية اليمنى عند B. تنحني الأشعة المنكسرة عند A وB بشكل أولي نحو الخطوط العمودية الهابطة على السطح، مما يجعل زاوية ثيتا اثنين في الاتجاه الرأسي. يتم رسم واجهة الموجة المنكسرة المتعامدة مع الأشعة المنكسرة والتي تصطدم بالسطح عند B prime. تصطدم واجهة الموجة هذه بانكسار الشعاع الساقط الأول عند نقطة تحمل علامة A prime وتجعل زاوية ثيتا ثنائية مع السطح.
    الشكل\(\PageIndex{5}\): هندسة قانون الانكسار من المتوسط 1 إلى المتوسط 2.
    الحل

    يتم مشاركة المقطع الموجود على السطح AB بواسطة كل من المثلث ABB داخل الوسط 1 والمثلث AA′B داخل الوسط 2. لاحظ أنه من الناحية الهندسية، تساوي الزاوية BAB' زاوية السقوط،\(θ_1\). وبالمثل،\(∠AB'A'\) هو\(θ_2\).

    يتم إعطاء طول B «بطريقتين:

    \ [AB'=\ dfrac {B'} {\ sin _1} =\ dfrac {AA'} {\ sin _2}. \ لا يوجد رقم\]

    عكس المعادلة واستبدال Aa'=cΔt/n 2 من الأعلى وبالمثل\(BB'=cΔt/n_1\)، نحصل على

    \ [\ dfrac {\ sin _1} {c\ دلتا t/n_1} =\ dfrac {\ sin _2} {c\ Delta t/n_2}. \ لا يوجد رقم\]

    إلغاء\(cΔt\) يسمح لنا بتبسيط هذه المعادلة في الشكل المألوف

    \ [\ underbrace {n_1\ sin _1=n_2\ sin _2} _ {\ text {\ قانون سنيل}}. \ لا يوجد رقم\]

    الأهمية

    على الرغم من أن قانون الانكسار تم إنشاؤه تجريبيًا بواسطة Snell، إلا أن اشتقاقه هنا يتطلب مبدأ Huygens وفهم أن سرعة الضوء مختلفة في الوسائط المختلفة.

    التمارين الرياضية\(\PageIndex{1}\)

    على سبيل المثال\(\PageIndex{1}\)، كان لدينا\(n_1<n_2\). إذا\(n_2\) تم تقليلها بحيث\(n_1>n_2\) تكون سرعة الضوء في المتوسط 2 أسرع من المتوسط 1، فماذا سيحدث لطول AA'؟ ماذا سيحدث للموجة الأمامية A' B ' واتجاه الشعاع المنكسر؟

    إجابة

    يصبح AA′ أطول، ويميل A'B بعيدًا عن السطح، ويميل الشعاع المنكسر بعيدًا عن المعتاد.

    يُظهر هذا التطبيق الصغير من Walter Fendt رسمًا متحركًا للانعكاس والانكسار باستخدام موجات Huygens أثناء التحكم في المعلمات. تأكد من النقر فوق «الخطوة التالية» لعرض الموجات. يمكنك رؤية جبهات الموجة المنعكسة والمكسرة تتشكل.

    الحيود

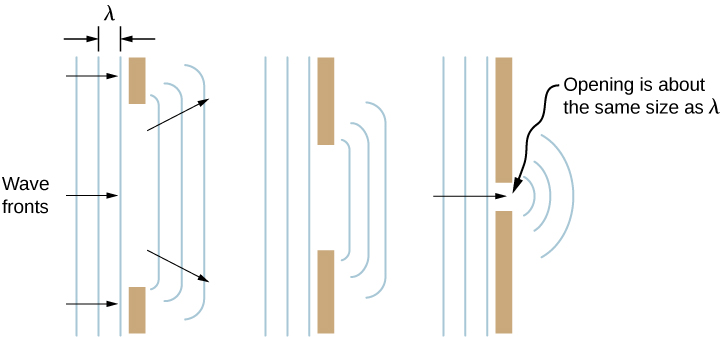
    ماذا يحدث عندما تمر موجة عبر فتحة، مثل الضوء الساطع من خلال باب مفتوح إلى غرفة مظلمة؟ بالنسبة للضوء، نلاحظ ظلًا حادًا للمدخل على أرضية الغرفة، ولا ينحني أي ضوء مرئي حول الزوايا إلى أجزاء أخرى من الغرفة. عندما يمر الصوت عبر الباب، نسمعه في كل مكان في الغرفة ، وبالتالي نلاحظ أن الصوت ينتشر عند المرور عبر مثل هذه الفتحة (الشكل\(\PageIndex{6}\)). ما الفرق بين سلوك الموجات الصوتية وموجات الضوء في هذه الحالة؟ الإجابة هي أن الضوء له أطوال موجية قصيرة جدًا ويعمل مثل الشعاع. يحتوي الصوت على أطوال موجية بترتيب حجم الباب وينحني حول الزوايا (لتردد 1000 هرتز،

    \ [\ لامدا =\ dfrac {c} {f} =\ dfrac {330\، م/ث} {1000\، s^ {−1}} =0.33\، م،\ لا رقم\]

    أصغر بثلاث مرات تقريبًا من عرض المدخل).

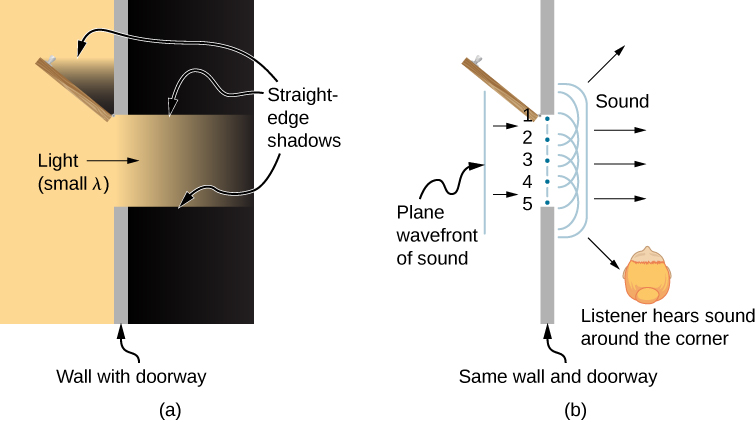
    الشكل (أ) عبارة عن منظر من أعلى لرسم تخطيطي لجدار يوجد فيه مدخل مفتوح. يمتد الجدار من أسفل المخطط إلى الأعلى، ويشكل المدخل فجوة في الجدار. يتم فتح الباب نفسه إلى اليسار ويتم وضعه على بعد حوالي خمس وأربعين درجة من الجدار الذي يدور عليه. الضوء، المسمى لامدا الصغير، يسقط من الجانب الأيسر من الجدار. يمر بعض الضوء عبر المدخل المفتوح. يحتوي الضوء الذي يمر عبر الباب على حواف حادة تتوافق مع ظلال الحواف المستقيمة أعلى وأسفل. يخلق الباب المفتوح أيضًا ظلًا مستقيمًا بينه وبين الجدار. يُظهر الجزء ب من الشكل مخططًا مشابهًا. يقترب الخط الموازي للجدار من الجدار من اليسار ويسمى موجة مستوية أمام الصوت. هناك خمس نقاط متباعدة بشكل متساوٍ عبر المدخل المفتوح، مصنفة من واحدة إلى خمس. تظهر نصف الدائرة على يمين هذه النقاط التي تدخل الغرفة على يمين الجدار. يمثل تقويم كل هذه الدوائر النصفية خطًا على شكل قوس مربع مغلق بزوايا مستديرة. هذا الخط يسمى الصوت. تظهر خمسة أشعة تشير من خط الأقواس إلى الغرفة على يمين الجدار. تشير ثلاثة من هذه الأشعة أفقيًا إلى اليمين، ويشير شعاع واحد إلى الأعلى وإلى اليمين، ويشير الشعاع الأخير إلى الأسفل وإلى اليمين. يشير هذا الشعاع الأخير إلى أذن شخص نراه من الأعلى والذي يُطلق عليه اسم المستمع يسمع صوتًا قريبًا.
    الشكل\(\PageIndex{6}\): (أ) الضوء الذي يمر عبر المدخل يصنع مخططًا حادًا على الأرض. نظرًا لأن الطول الموجي للضوء صغير جدًا مقارنة بحجم الباب، فإنه يعمل مثل الشعاع. (ب) تنحني الموجات الصوتية في جميع أجزاء الغرفة، وهو تأثير موجة، لأن طولها الموجي يشبه حجم الباب.

    إذا قمنا بتمرير الضوء من خلال فتحات أصغر مثل الشقوق، فيمكننا استخدام مبدأ Huygens لنرى أن الضوء ينحني كما يفعل الصوت (الشكل\(\PageIndex{7}\)). يُطلق على انحناء الموجة حول حواف الفتحة أو العائق اسم الحيود. الحيود هو خاصية موجية ويحدث لجميع أنواع الموجات. إذا لوحظ الانحراف لبعض الظواهر، فهذا دليل على أن الظاهرة هي موجة. وبالتالي، فإن الحيود الأفقي لشعاع الليزر بعد مروره عبر الشقوق في الشكل\(\PageIndex{7}\) هو دليل على أن الضوء عبارة عن موجة.

    يوضِّح الشكل ثلاثة رسوم بيانية توضِّح الموجات المنتشرة عند المرور عبر الفتحات ذات الأحجام المختلفة. كل رسم توضيحي عبارة عن منظر علوي، ويتم تمثيل واجهات موجات الطائرة الساقطة بخطوط عمودية. الطول الموجي، lambda، هو المسافة بين الخطوط المتجاورة وهو نفسه في جميع المخططات الثلاثة. يُظهر الرسم التخطيطي الأول جبهات الموجة التي تمر عبر فتحة واسعة مقارنة بالطول الموجي. تتميز واجهات الموجة التي تظهر على الجانب الآخر من الفتحة بانحناء بسيط عند الحواف. يُظهر الرسم التخطيطي الثاني جبهات الموجة التي تمر عبر فتحة أصغر. تتعرض الأمواج لمزيد من الانحناء ولكن لا يزال لها جزء مستقيم. يوضِّح الشكل الثالث جبهات موجية تمر عبر فتحة لها نفس حجم الطول الموجي تقريبًا. تُظهر هذه الموجات انحناءًا كبيرًا، وفي الواقع، تبدو دائرية وليست مستقيمة.
    الشكل\(\PageIndex{7}\): تم تطبيق مبدأ Huygens على واجهة الموجة الطائرة التي تصطدم بالفتحة. تنحني حواف الموجة الأمامية بعد المرور عبر الفتحة، وهي عملية تسمى الحيود. تكون كمية الانحناء أكثر تطرفًا بالنسبة للفتحة الصغيرة، بما يتفق مع حقيقة أن خصائص الموجة تكون أكثر وضوحًا للتفاعلات مع الأجسام بنفس حجم الطول الموجي.