1.8: الاستقطاب
- Page ID
- 196648
في نهاية هذا القسم، ستكون قادرًا على:
- اشرح التغيير في الكثافة عندما يمر الضوء المستقطب عبر مرشح استقطابي
- احسب تأثير الاستقطاب بالانعكاس وزاوية بروستر
- وصف تأثير الاستقطاب عن طريق التشتت
- شرح استخدام المواد المستقطبة في أجهزة مثل شاشات LCD
النظارات الشمسية المستقطبة مألوفة لمعظمنا. لديهم قدرة خاصة على قطع وهج الضوء المنعكس من الماء أو الزجاج (الشكل\(\PageIndex{1}\)). لديهم هذه القدرة بسبب الموجة المميزة للضوء والتي تسمى الاستقطاب. ما هو الاستقطاب؟ كيف يتم إنتاجها؟ ما هي بعض استخداماته؟ ترتبط الإجابات على هذه الأسئلة بالطابع الموجي للضوء.

قانون مالوس
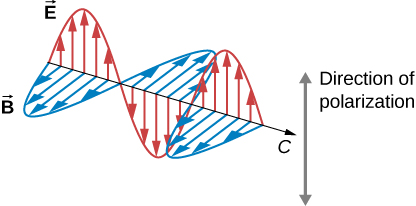
الضوء هو نوع واحد من الموجات الكهرومغناطيسية (EM). موجات EM هي موجات عرضية تتكون من مجالات كهربائية ومغناطيسية مختلفة تتأرجح عموديًا على اتجاه الانتشار (الشكل \(\PageIndex{2}\)). ومع ذلك، بشكل عام، لا توجد اتجاهات محددة لتذبذبات المجالات الكهربائية والمغناطيسية؛ فهي تهتز في أي مستوى موجه عشوائيًا عموديًا على اتجاه الانتشار. الاستقطاب هو السمة التي تشير إلى أن تذبذبات الموجة لها اتجاه محدد بالنسبة لاتجاه انتشار الموجة. (هذا ليس نفس نوع الاستقطاب الذي تمت مناقشته لفصل الشحنات.) ويقال إن الموجات التي لها مثل هذا الاتجاه مستقطبة. بالنسبة لموجة EM، نحدد اتجاه الاستقطاب ليكون الاتجاه الموازي للمجال الكهربائي. وهكذا، يمكننا أن نفكر في سهام المجال الكهربائي على أنها تُظهر اتجاه الاستقطاب، كما في الشكل \(\PageIndex{2}\).
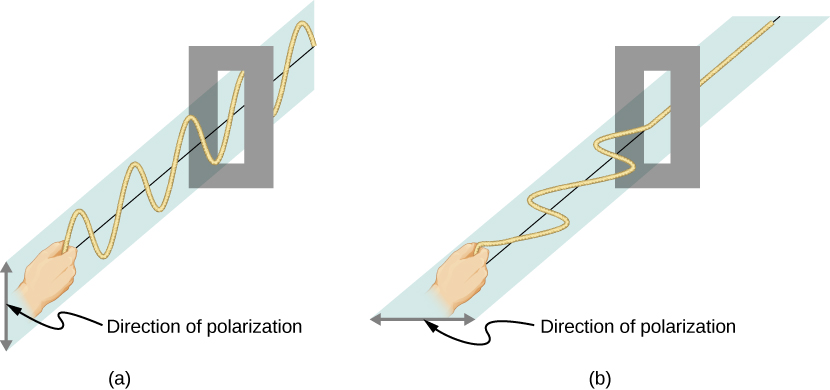
لمزيد من الفحص، ضع في اعتبارك الموجات العرضية في الحبال الموضحة في الشكل\(\PageIndex{3}\). تكون التذبذبات في حبل واحد في مستوى عمودي ويقال إنها مستقطبة رأسيًا. أما تلك الموجودة في الحبل الآخر فهي في مستوى أفقي ومستقطبة أفقيًا. في حالة وضع شق عمودي على الحبل الأول، تمر الأمواج من خلاله. ومع ذلك، فإن الشق الرأسي يحجب الموجات المستقطبة أفقيًا. بالنسبة لموجات EM، يكون اتجاه المجال الكهربائي مشابهًا للاضطرابات على الحبال.
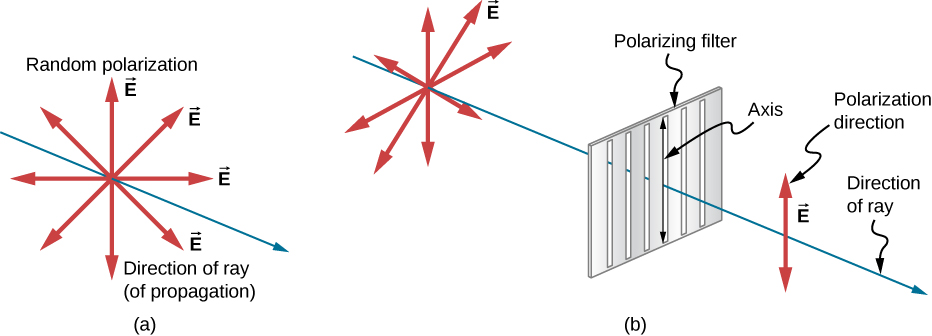
تنتج الشمس والعديد من مصادر الضوء الأخرى موجات تحتوي على المجالات الكهربائية في اتجاهات عشوائية (الشكل\(\PageIndex{1a}\)). ويقال إن هذا الضوء غير مستقطب، لأنه يتكون من العديد من الموجات مع جميع الاتجاهات الممكنة للاستقطاب. تعمل مواد بولارويد - التي اخترعها مؤسس شركة بولارويد، إدوين لاند - كشق استقطابي للضوء، مما يسمح فقط بمرور الاستقطاب في اتجاه واحد. تتكون المرشحات المستقطبة من جزيئات طويلة محاذاة في اتجاه واحد. إذا فكرنا في الجزيئات كالعديد من الشقوق، المماثلة لتلك الموجودة في الحبال المتذبذبة، يمكننا أن نفهم لماذا يمكن للضوء ذي الاستقطاب المحدد فقط أن يمر. محور المرشح المستقطب هو الاتجاه الذي يمر فيه المرشح بالحقل الكهربائي لموجة EM.
\(\PageIndex{5}\)يوضح الشكل تأثير اثنين من الفلاتر المستقطبة على الضوء غير المستقطب في الأصل. يقوم المرشح الأول باستقطاب الضوء على طول محوره. عندما تتم محاذاة محاور الفلاتر الأولى والثانية (بالتوازي)، فإن كل الضوء المستقطب الذي يمر به الفلتر الأول يتم تمريره أيضًا بواسطة الفلتر الثاني. إذا تم تدوير مرشح الاستقطاب الثاني، يتم تمرير مكون الضوء الموازي لمحور المرشح الثاني فقط. عندما تكون المحاور متعامدة، لا يمر أي ضوء بواسطة الفلتر الثاني.
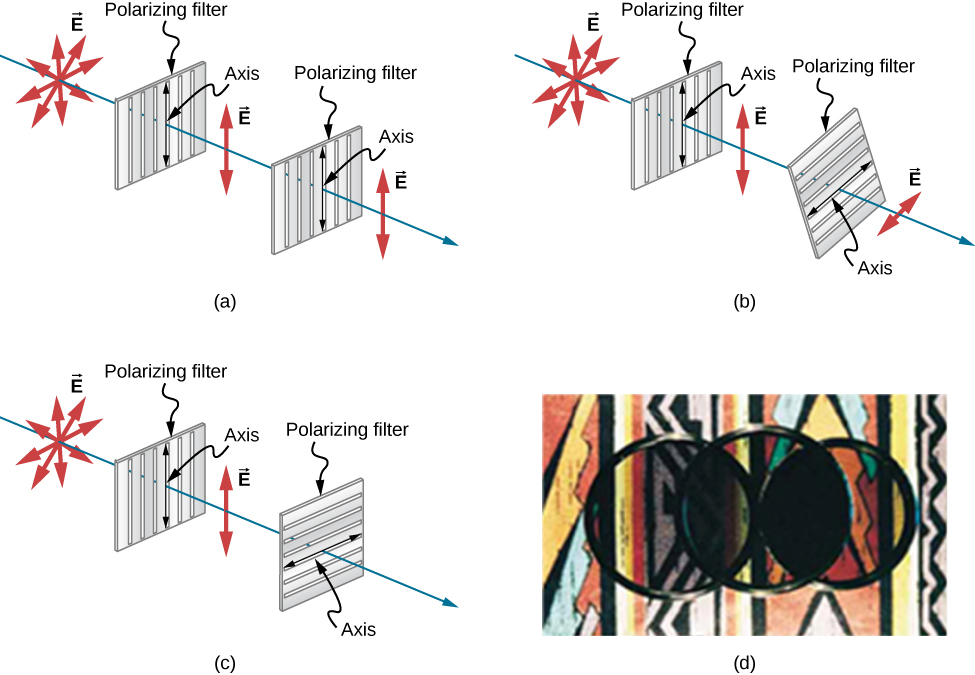
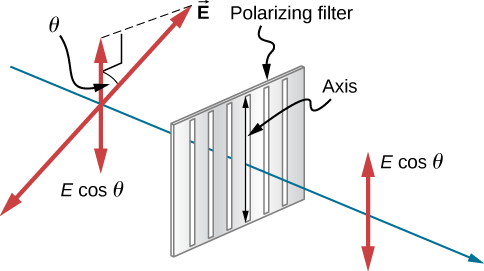
يتم تمرير مكون موجة EM الموازي لمحور المرشح فقط. دعونا نسمي الزاوية بين اتجاه الاستقطاب ومحور المرشح. إذا كان المجال الكهربائي ذا سعة E، فإن الجزء المرسل من الموجة له سعة\(E\cos θ \) (الشكل\(\PageIndex{6}\)). نظرًا لأن شدة الموجة تتناسب مع مربع اتساعها، فإن الكثافة I للموجة المرسلة ترتبط بالموجة الساقطة بـ
\ [I=I_0\ cos^2\ التسمية { قانون مالوس}\ بدون رقم\]
\(I_0\)أين شدة الموجة المستقطبة قبل المرور عبر الفلتر. تُعرف هذه المعادلة باسم قانون مالوس.
تساعدك هذه الرسوم المتحركة للفيزياء مفتوحة المصدر على تصور متجهات المجال الكهربائي عندما يواجه الضوء مرشحًا مستقطبًا. يمكنك تدوير الفلتر - لاحظ أن الزاوية المعروضة بالراديان. يمكنك أيضًا تدوير الرسوم المتحركة للتصور ثلاثي الأبعاد.
مثال \(\PageIndex{1}\): حساب تقليل الكثافة بواسطة مرشح استقطابي
ما الزاوية اللازمة بين اتجاه الضوء المستقطب ومحور المرشح المستقطب لتقليل شدته بنسبة 90.0%؟
إستراتيجية
عندما تنخفض الكثافة بنسبة 90.0٪، فإنها تكون 10.0٪ أو 0.100 ضعف قيمتها الأصلية. وهذا هو، I=0.100I 0. باستخدام هذه المعلومات، يمكن استخدام المعادلة I=I 0 cos 2 لحل الزاوية المطلوبة.
الحل
يعطي حل قانون مالوس (المعادلة\ المرجع {قانون مالوس})\(\cos θ\) واستبدال العلاقة بين I و I 0
\[\cos θ=\dfrac{I}{I_0}=\frac{0.100I_0}{I_0}=0.3162. \nonumber \]
حل مشكلة\(θ\) العوائد
\[θ=\cos^{−1}0.3162=71.6°. \nonumber \]
الدلالة
هناك حاجة إلى زاوية كبيرة إلى حد ما بين اتجاه الاستقطاب ومحور المرشح لتقليل الكثافة إلى 10.0٪ من قيمتها الأصلية. يبدو هذا معقولًا بناءً على تجربة الأفلام المستقطبة. من المثير للاهتمام أنه بزاوية 45 درجة، يتم تقليل الكثافة إلى 50٪ من قيمتها الأصلية. لاحظ أن 71.6 درجة تساوي 18.4 درجة من تقليل الكثافة إلى الصفر، وأنه بزاوية 18.4 درجة، تنخفض الكثافة إلى 90٪ من قيمتها الأصلية، مما يدل على التماثل.
على الرغم من أننا لم نحدد الاتجاه في المثال\(\PageIndex{1}\)، لنفترض أن مرشح الاستقطاب تم تدويره في اتجاه عقارب الساعة بمقدار 71.6 درجة لتقليل شدة الضوء بنسبة 90.0٪. ماذا سيكون انخفاض الكثافة إذا تم تدوير المرشح المستقطب عكس اتجاه عقارب الساعة بمقدار 71.6 درجة؟
- إجابة
-
أيضًا 90.0%
الاستقطاب بالانعكاس
الآن، ربما يمكنك تخمين أن النظارات الشمسية المستقطبة تقلل من وهج الضوء المنعكس، لأن هذا الضوء مستقطب. يمكنك التحقق من ذلك بنفسك عن طريق حمل النظارات الشمسية المستقطبة أمامك وتدويرها أثناء النظر إلى الضوء المنعكس من الماء أو الزجاج. عند تدوير النظارات الشمسية، ستلاحظ أن الضوء يصبح ساطعًا وخافتًا، ولكن ليس أسود تمامًا. هذا يعني أن الضوء المنعكس مستقطب جزئيًا ولا يمكن حظره تمامًا بواسطة مرشح استقطابي.
\(\PageIndex{7}\)يوضح الشكل ما يحدث عندما ينعكس الضوء غير المستقطب من السطح. ينكسر الضوء المستقطب عموديًا بشكل تفضيلي على السطح، لذلك يتم ترك الضوء المنعكس أكثر استقطابًا أفقيًا. أسباب هذه الظاهرة خارجة عن نطاق هذا النص، لكن الذاكرة الملائمة لتذكر ذلك هي تخيل اتجاه الاستقطاب ليكون مثل السهم. الاستقطاب العمودي يشبه السهم العمودي على السطح ومن المرجح أن يلتصق ولا ينعكس. الاستقطاب الأفقي يشبه السهم المرتد على جانبه ومن المرجح أن ينعكس. وبالتالي فإن النظارات الشمسية ذات المحاور الرأسية تحجب الضوء المنعكس أكثر من الضوء غير المستقطب من مصادر أخرى.
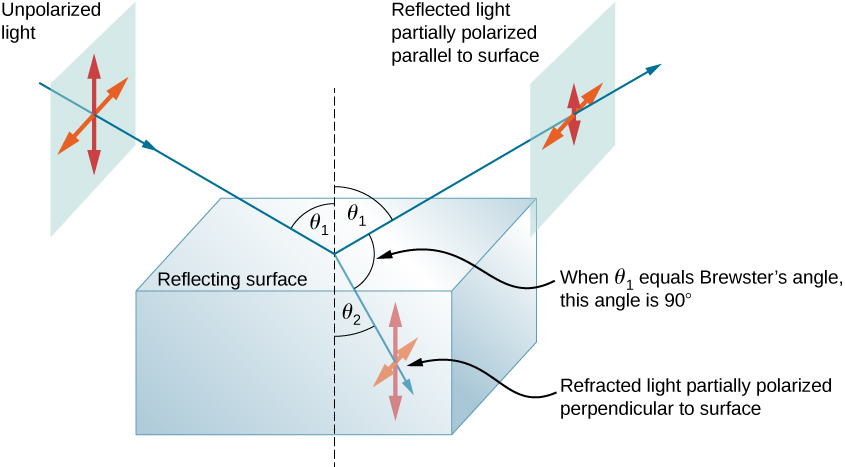
نظرًا لأن جزء الضوء الذي لا ينعكس ينكسر، فإن مقدار الاستقطاب يعتمد على مؤشرات انكسار الوسائط المعنية. يمكن إثبات أن الضوء المنعكس مستقطب تمامًا بزاوية الانعكاس b المعطاة بواسطة
\[tan \, θ_b=\frac{n_2}{n_1} \nonumber \]
حيث n 1 هو الوسيط الذي ينتقل فيه الضوء الساقط والمنعكس و n 2 هو معامل انكسار الوسط الذي يشكل الواجهة التي تعكس الضوء. تُعرف هذه المعادلة باسم قانون بروستر، وتُعرف b بزاوية بروستر، التي سُميت على اسم عالم الفيزياء الاسكتلندي في القرن التاسع عشر الذي اكتشفها.
تُظهر هذه الرسوم المتحركة لفيزياء المصادر المفتوحة الضوء الساقط والمنعكس والمكسور في صورة أشعة وموجات كهرومغناطيسية. حاول تدوير الرسوم المتحركة للتصور ثلاثي الأبعاد وأيضًا تغيير زاوية الإصابة. بالقرب من زاوية بروستر، يصبح الضوء المنعكس مستقطبًا للغاية.
مثال \(\PageIndex{2}\): حساب الاستقطاب بالانعكاس
(أ) ما هي الزاوية التي سيستقطب فيها الضوء المنتقل في الهواء أفقيًا تمامًا عند انعكاسه من الماء؟ (ب) من الزجاج؟
إستراتيجية
كل ما نحتاجه لحل هذه المشاكل هو مؤشرات الانكسار. يحتوي الهواء على n 1 = 1.00، والماء n 2 = 1.333، وزجاج التاج له n′ 2 = 1.520. \(tan \, θ_b=\frac{n_2}{n_1}\)يمكن تطبيق المعادلة مباشرةً لإيجاد b في كل حالة.
الحل
أ- وضع الكميات المعروفة في المعادلة
\[\tan \, θ_b=\frac{n_2}{n_1} \nonumber \]
يعطي
\[\tan \, θ_b=\frac{n_2}{n_1}=\frac{1.333}{1.00}=1.333. \nonumber \]
حل الزاوية ب الناتجة
\[θ_b=tan^{−1}1.333=53.1°. \nonumber \]
ب- وبالمثل، بالنسبة لزجاج التاج والهواء،
\[tan \, θ′_b=\frac{n′_2}{n_1}=\frac{1.520}{1.00}=1.52. \nonumber \]
وهكذا،
\[θ′_b=tan^{−1}1.52=56.7°. \nonumber \]
الدلالة
يمكن حجب الضوء المنعكس في هذه الزوايا تمامًا عن طريق مرشح استقطابي جيد مثبت بمحوره الرأسي. تتشابه زاوية بروستر للماء والهواء مع تلك الخاصة بالزجاج والهواء، بحيث تكون النظارات الشمسية فعالة بنفس القدر للضوء المنعكس من الماء أو الزجاج في ظروف مماثلة. الضوء الذي لا ينعكس ينكسر في هذه الوسائط. لذلك، عند زاوية سقوط تساوي زاوية بروستر، يكون الضوء المنكسر مستقطبًا رأسيًا قليلاً. لا يتم استقطابه رأسيًا بالكامل، لأنه لا ينعكس سوى جزء صغير من الضوء الساقط، لذلك ينكسر قدر كبير من الضوء المستقطب أفقيًا.
ماذا يحدث بزاوية بروستر إذا كان الضوء الساقط الأصلي مستقطبًا رأسيًا بنسبة 100٪ بالفعل؟
- إجابة
-
سيكون هناك انكسار فقط ولكن لن يكون هناك انعكاس.
التفسير الذري للمرشحات المستقطبة
تحتوي المرشحات المستقطبة على محور استقطاب يعمل كشق. يمرر هذا الشق موجات EM (الضوء المرئي غالبًا) التي لها مجال كهربائي موازٍ للمحور. يتم تحقيق ذلك من خلال الجزيئات الطويلة المحاذية عموديًا على المحور، كما هو موضح في الشكل \(\PageIndex{8}\).
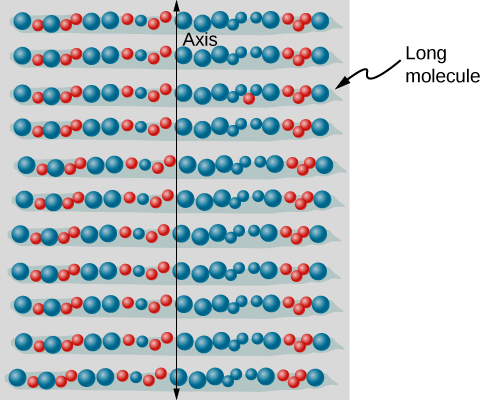
\(\PageIndex{9}\)يوضح الشكل كيفية امتصاص مكون المجال الكهربائي الموازي للجزيئات الطويلة. تتكون موجة EM من مجالات كهربائية ومغناطيسية متذبذبة. المجال الكهربائي قوي مقارنة بالمجال المغناطيسي وهو أكثر فعالية في ممارسة القوة على الشحنات في الجزيئات. الجسيمات المشحونة الأكثر تأثراً هي الإلكترونات، لأن كتل الإلكترون صغيرة. إذا اضطر الإلكترون إلى التذبذب، يمكنه امتصاص الطاقة من موجة EM. هذا يقلل من المجال في الموجة، وبالتالي يقلل من شدتها. في الجزيئات الطويلة، يمكن للإلكترونات أن تتأرجح بسهولة بالتوازي مع الجزيء مقارنة بالاتجاه العمودي. ترتبط الإلكترونات بالجزيء وتكون أكثر تقييدًا في حركتها عموديًا على الجزيء. وبالتالي، يمكن للإلكترونات أن تمتص موجات EM التي تحتوي على مكون من مجالها الكهربائي الموازي للجزيء. تكون الإلكترونات أقل استجابة بكثير للمجالات الكهربائية العمودية على الجزيء وتسمح لهذه الحقول بالمرور. وبالتالي، يكون محور المرشح المستقطب عموديًا على طول الجزيء.
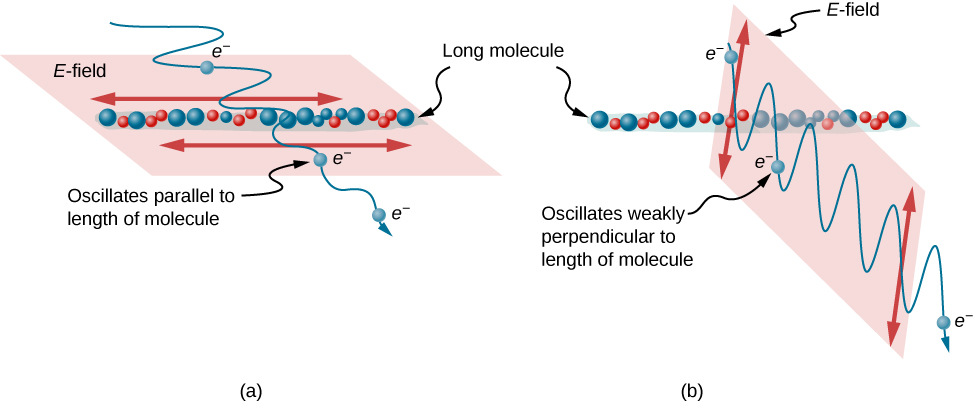
الاستقطاب عن طريق التشتت
إذا كنت تحمل النظارات الشمسية المستقطبة أمامك وقمت بتدويرها أثناء النظر إلى السماء الزرقاء، فسترى السماء مشرقة وخافتة. هذا مؤشر واضح على أن الضوء المنتشر بالهواء مستقطب جزئيًا. \(\PageIndex{10}\)يساعد الشكل على توضيح كيفية حدوث ذلك. نظرًا لأن الضوء عبارة عن موجة EM عرضية، فإنه يهتز إلكترونات جزيئات الهواء عموديًا على الاتجاه الذي يتحرك فيه. ثم تشع الإلكترونات مثل الهوائيات الصغيرة. نظرًا لأنها تتأرجح عموديًا على اتجاه شعاع الضوء، فإنها تنتج إشعاع EM المستقطب عموديًا على اتجاه الشعاع. عند عرض الضوء على طول خط عمودي على الشعاع الأصلي، كما في الشكل، لا يمكن أن يكون هناك استقطاب في الضوء المتناثر الموازي للشعاع الأصلي، لأن ذلك يتطلب أن يكون الشعاع الأصلي موجة طولية. على طول اتجاهات أخرى، يمكن عرض أحد مكونات الاستقطاب الآخر على طول خط الرؤية، ويتم استقطاب الضوء المتناثر جزئيًا فقط. علاوة على ذلك، يمكن أن يجلب التشتت المتعدد الضوء إلى عينيك من اتجاهات أخرى ويمكن أن يحتوي على استقطابات مختلفة.
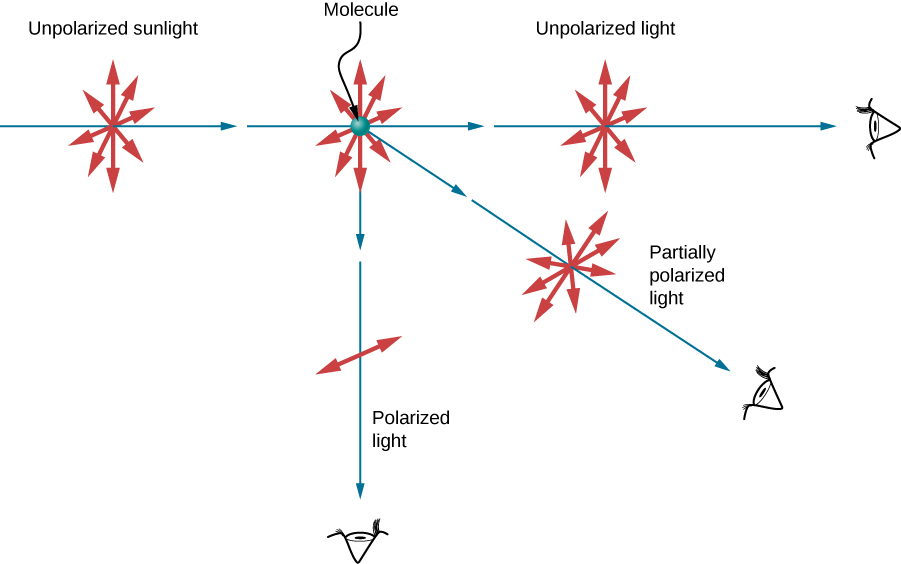
يمكن تعتيم صور السماء عن طريق الفلاتر المستقطبة، وهي خدعة يستخدمها العديد من المصورين لجعل السحب أكثر إشراقًا من خلال التباين. يمكن أن يؤدي التشتت من الجسيمات الأخرى، مثل الدخان أو الغبار، أيضًا إلى استقطاب الضوء. يمكن أن يكون اكتشاف الاستقطاب في موجات EM المتناثرة أداة تحليلية مفيدة في تحديد مصدر التشتت.
يتم استخدام مجموعة من التأثيرات البصرية في النظارات الشمسية. بالإضافة إلى كونها مستقطبة، قد تحتوي النظارات الشمسية على أصباغ ملونة مضمنة فيها، بينما يستخدم البعض الآخر طلاءًا غير عاكس أو عاكس. ومن التطورات الحديثة العدسات الفوتوكرومية، التي تصبح داكنة في ضوء الشمس وتصبح واضحة في الداخل. العدسات الفوتوكرومية مدمجة بجزيئات عضوية من البلورات الدقيقة التي تغير خصائصها عند تعرضها للأشعة فوق البنفسجية في ضوء الشمس، ولكنها تصبح واضحة في الإضاءة الاصطناعية بدون الأشعة فوق البنفسجية.
البلورات السائلة وتأثيرات الاستقطاب الأخرى في المواد
على الرغم من أنك تدرك بلا شك شاشات الكريستال السائل (LCD) الموجودة في الساعات والآلات الحاسبة وشاشات الكمبيوتر والهواتف المحمولة وأجهزة التلفزيون ذات الشاشات المسطحة والعديد من الأماكن الأخرى، فقد لا تدرك أنها تستند إلى الاستقطاب. سميت البلورات السائلة بهذا الاسم لأن جزيئاتها يمكن أن تتماشى على الرغم من وجودها في سائل. تتمتع البلورات السائلة بخاصية قدرتها على تدوير استقطاب الضوء الذي يمر عبرها بمقدار 90 درجة. علاوة على ذلك، يمكن إيقاف تشغيل هذه الخاصية من خلال تطبيق الجهد، كما هو موضح في الشكل\(\PageIndex{11}\). من الممكن معالجة هذه الخاصية بسرعة وفي مناطق صغيرة ومحددة جيدًا لإنشاء أنماط التباين التي نراها في العديد من أجهزة LCD.
في أجهزة تلفزيون LCD ذات الشاشات المسطحة، يتم توليد ضوء كبير في الجزء الخلفي من التلفزيون. ينتقل الضوء إلى الشاشة الأمامية من خلال ملايين الوحدات الصغيرة التي تسمى وحدات البكسل (عناصر الصورة). يظهر أحد هذه العناصر في الشكل\(\PageIndex{11}\). تحتوي كل وحدة على ثلاث خلايا، مع مرشحات حمراء أو زرقاء أو خضراء، يتم التحكم في كل منها بشكل مستقل. عندما يتم إيقاف تشغيل الجهد عبر البلورة السائلة، تقوم البلورة السائلة بتمرير الضوء من خلال مرشح معين. يمكننا تغيير تباين الصورة من خلال تغيير قوة الجهد المطبق على البلورة السائلة.
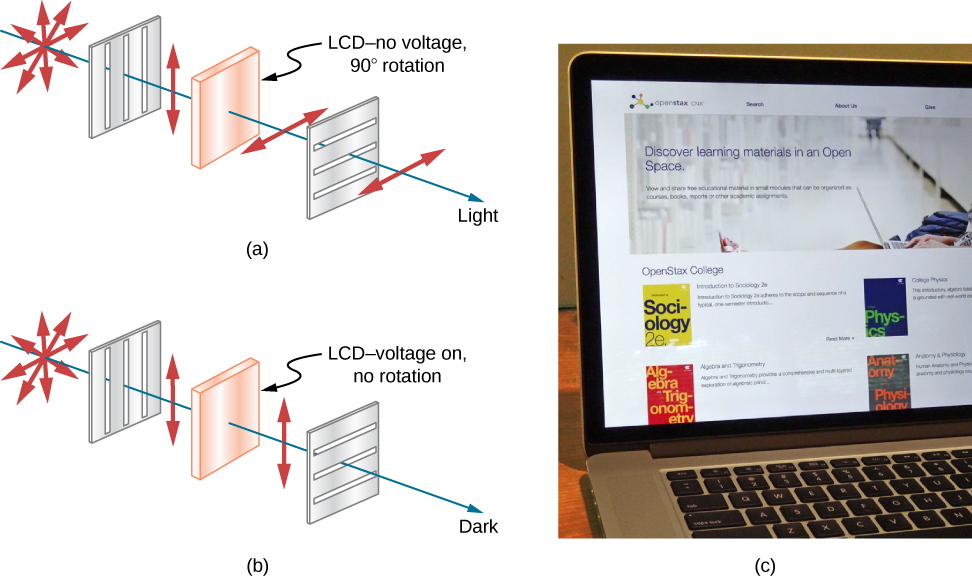
تقوم العديد من البلورات والحلول بتدوير مستوى استقطاب الضوء الذي يمر عبرها. ويقال إن هذه المواد نشطة بصريًا. تشمل الأمثلة ماء السكر والأنسولين والكولاجين (الشكل\(\PageIndex{11}\)). بالإضافة إلى الاعتماد على نوع المادة، تعتمد كمية واتجاه الدوران على عدة عوامل أخرى. ومن بين هذه العوامل تركيز المادة والمسافة التي يقطعها الضوء خلالها والطول الموجي للضوء. يرجع النشاط البصري إلى الشكل غير المتماثل للجزيئات في المادة، مثل كونها حلزونية. وبالتالي يمكن استخدام قياسات دوران الضوء المستقطب الذي يمر عبر المواد لقياس التركيزات، وهي تقنية قياسية للسكريات. يمكن أن يقدم أيضًا معلومات عن أشكال الجزيئات، مثل البروتينات، والعوامل التي تؤثر على أشكالها، مثل درجة الحرارة ودرجة الحموضة.
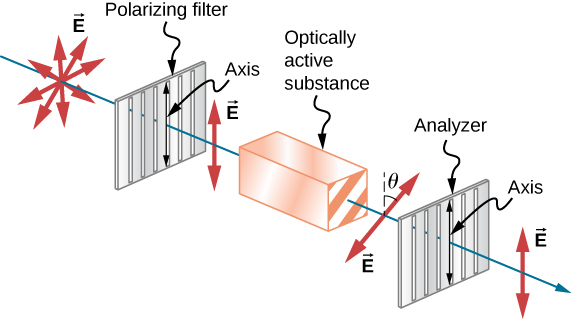
يصبح الزجاج والبلاستيك نشطين بصريًا عند الإجهاد: كلما زاد الضغط، زاد التأثير. يمكن إجراء تحليل الضغط البصري على الأشكال المعقدة عن طريق صنع نماذج بلاستيكية لها ومراقبتها من خلال الفلاتر المتقاطعة، كما هو موضح في الشكل \(\PageIndex{12}\). من الواضح أن التأثير يعتمد على الطول الموجي وكذلك الإجهاد. يستخدم الاعتماد على الطول الموجي أحيانًا أيضًا لأغراض فنية.

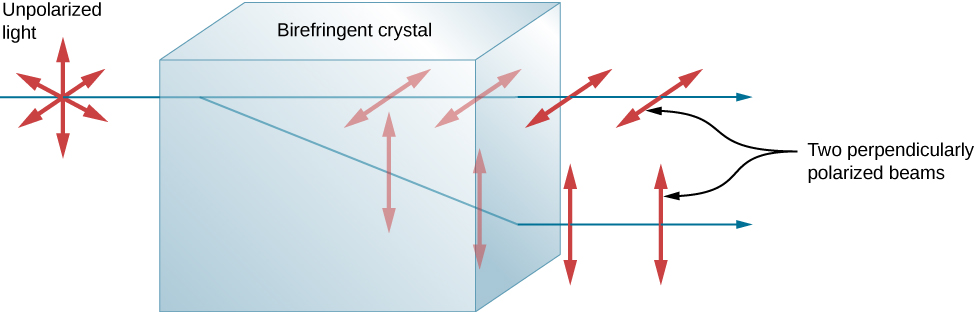
ظاهرة أخرى مثيرة للاهتمام مرتبطة بالضوء المستقطب هي قدرة بعض البلورات على تقسيم شعاع الضوء غير المستقطب إلى شعاعين مستقطبين. يحدث هذا لأن البلورة لها قيمة واحدة لمعامل انكسار الضوء المستقطب ولكن قيمة مختلفة لمؤشر انكسار الضوء المستقطب في الاتجاه العمودي، بحيث يكون لكل مكون زاوية انكسار خاصة به. يُقال إن هذه البلورات أحادية الانكسار، وعندما تتم محاذاتها بشكل صحيح، ستظهر شعاعتان مستقطبتان بشكل عمودي من البلورة (الشكل\(\PageIndex{14}\)). يمكن استخدام البلورات ثنائية الانكسار لإنتاج أشعة مستقطبة من الضوء غير المستقطب. تمتص بعض المواد ثنائية الانكسار بشكل تفضيلي أحد الاستقطابات. تسمى هذه المواد ثنائية اللون ويمكن أن تنتج الاستقطاب من خلال هذا الامتصاص التفضيلي. هذه هي الطريقة الأساسية التي تعمل بها المرشحات المستقطبة والمستقطبات الأخرى.