1.4: الانكسار

Last updated
Save as PDF

Page ID: 196671

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

وصف كيفية تغيير الأشعة لاتجاهها عند دخول وسيط
تطبيق قانون الانكسار في حل المشكلات

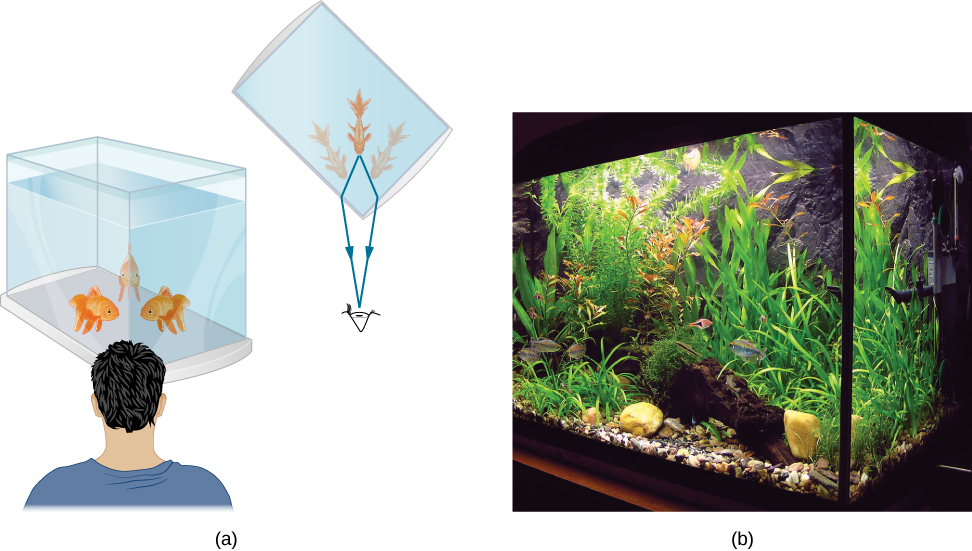
قد تلاحظ غالبًا بعض الأشياء الغريبة عند النظر إلى حوض الأسماك. على سبيل المثال، قد ترى نفس السمكة تظهر في مكانين مختلفين (الشكل\(\PageIndex{1}\)). يحدث هذا لأن الضوء القادم من السمكة إليك يغير اتجاهه عندما يغادر الخزان، وفي هذه الحالة، يمكنه السير في مسارين مختلفين للوصول إلى عينيك. يُطلق على تغيير اتجاه شعاع الضوء (يُطلق عليه بشكل فضفاض الانحناء) عندما يمر عبر مواد ذات مؤشرات انكسار مختلفة اسم الانكسار ويرتبط بالتغيرات في سرعة الضوء\(v=c/n\). الانكسار مسؤول عن مجموعة هائلة من الظواهر البصرية، من تأثير العدسات إلى نقل البيانات عبر الألياف الضوئية.

يُظهر الشكل أ رسمًا لشخص ينظر إلى زاوية حوض السمك. تظهر سمكة في الزاوية كصورة مزدوجة للأسماك، صورة واحدة تتكون من أشعة تمر عبر كل جانب من الجانبين المجتمعين في زاوية الخزان. يعرض الشكل (ب) صورة لحالة مماثلة. — الشكل\(\PageIndex{1}\): (أ) عند النظر إلى حوض السمك كما هو موضح، يمكننا رؤية نفس السمكة في موقعين مختلفين، لأن الضوء يغير الاتجاهات عندما يمر من الماء إلى الهواء. في هذه الحالة، يمكن للضوء أن يصل إلى الراصد من خلال مسارين مختلفين، لذلك يبدو أن الأسماك في مكانين مختلفين. يسمى انحناء الضوء هذا بالانكسار وهو مسؤول عن العديد من الظواهر البصرية. (ب) تُظهر هذه الصورة انكسار الضوء من سمكة بالقرب من قمة حوض أسماك.

\(\PageIndex{2}\)يوضح الشكل كيف يغير شعاع الضوء اتجاهه عندما يمر من وسط إلى آخر. كما كان الحال من قبل، يتم قياس الزوايا بالنسبة إلى العمود العمودي على السطح عند النقطة التي يعبر فيها شعاع الضوء. (ينعكس بعض الضوء الساقط من السطح، لكننا الآن نركز على الضوء الذي يتم إرساله.) يعتمد التغيير في اتجاه شعاع الضوء على القيم النسبية لمؤشرات الانكسار للوسيلتين المعنيتين. في الحالات المعروضة، يحتوي المتوسط 2 على معامل انكسار أكبر من المتوسط 1. لاحظ أنه كما هو موضح في الشكل\(\PageIndex{1a}\)، يتحرك اتجاه الشعاع بالقرب من العمود عندما يتقدم من وسط بمعامل انكسار منخفض إلى وسيط بمعامل انكسار أعلى. وعلى العكس من ذلك\(\PageIndex{1b}\)، كما هو موضح في الشكل، يتحرك اتجاه الشعاع بعيدًا عن العمودي عندما يتقدم من وسط ذي معامل انكسار أعلى إلى وسيط بمعامل انكسار أقل. المسار يمكن عكسه تمامًا.

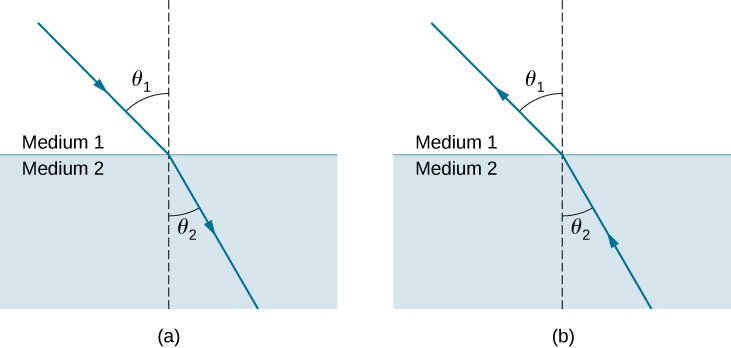
الشكل هو رسم توضيحي لانكسار الضوء عند واجهة بين وسيطين. في كلا الشكلين، يكون الوسيط 1 أعلى من المتوسط 2 والواجهة أفقية ويتم رسم شعاع ينكسر عند الواجهة. يتم رسم خط عمودي على الواجهة عند نقطة الإصابة. في الشكل أ، يسقط الضوء من الأعلى، ويمر من المتوسط 1 إلى المتوسط 2. في الوسط 1، يصنع الشعاع الساقط زاوية ثيتا واحدة على العمود، بينما يصنع الشعاع المنكسر في الوسط 2 زاوية أصغر ثيتا على العمود. في الشكل (ب)، يسقط الضوء من الأسفل، ويمر من المتوسط 2 إلى المتوسط 1. في الوسط 2، يصنع الشعاع الساقط زاوية ثيتا اثنين على العمود، بينما يصنع الشعاع المنكسر في الوسط 1 زاوية أكبر بمقدار واحد على العمود. ثيتا واحد في الشكل أ يساوي الزاوية ثيتا واحدة في الشكل ب، وبالمثل، فإن ثيتا 2 في الشكل أ تساوي الزاوية ثيتا اثنين في الشكل ب. — الشكل\(\PageIndex{2}\): يعتمد التغيير في اتجاه شعاع الضوء على كيفية تغير معامل الانكسار عندما ينتقل من وسط إلى آخر. في الحالات الموضحة هنا، يكون معامل الانكسار في الوسط 2 أكبر منه في المتوسط 1. (أ) يتحرك شعاع الضوء بالقرب من العمود عندما يدخل وسط بمعامل انكسار أعلى. (ب) يتحرك شعاع الضوء بعيدًا عن العمود عند دخوله إلى وسط بمعامل انكسار أقل.

يعتمد مقدار تغيير شعاع الضوء لاتجاهه على كل من زاوية السقوط ومقدار تغير السرعة. بالنسبة لشعاع بزاوية سقوط معينة، يؤدي التغيير الكبير في السرعة إلى تغيير كبير في الاتجاه وبالتالي تغيير كبير في الزاوية. العلاقة الرياضية الدقيقة هي قانون الانكسار، أو قانون سنيل، بعد عالم الرياضيات الهولندي ويليبرورد سنيل (1591-1626)، الذي اكتشفه عام 1621. يرد قانون الانكسار في شكل معادلة كـ

\[n_1 \, \sin \, θ_1=n_2 \, \sin \, θ_2. \label{snell's law} \]

هنا (n_1\)\(n_2\) وهي مؤشرات الانكسار للوسائط 1 و 2،\(θ_2\) وهي الزوايا بين الأشعة والعمودي في الوسائط 1 و 2.\(θ_1\) يُطلق على الشعاع الوارد اسم الشعاع الساقط، ويُسمى الشعاع الصادر بالشعاع المنكسر، والزوايا المرتبطة به هي زاوية السقوط والزاوية الانكسار، على التوالي.

أظهرت تجارب سنيل أنه يتم الامتثال لقانون الانكسار وأنه\(n\) يمكن تخصيص معامل الانكسار المميز لوسيط معين وقياس قيمته. لم يكن سنيل يدرك أن سرعة الضوء تختلف باختلاف الوسائط، وهي حقيقة أساسية تُستخدم عندما نستمد قانون الانكسار نظريًا باستخدام مبدأ Huygens.

مثال\(\PageIndex{1}\): Determining the Index of Refraction

أوجد معامل الانكسار للمتوسط 2 في الشكل\(\PageIndex{1a}\)، بافتراض أن المتوسط 1 هو الهواء، وإذا كانت زاوية السقوط 30.0 درجة وزاوية الانكسار 22.0 درجة.

إستراتيجية

يعتبر مؤشر الانكسار للهواء 1 في معظم الحالات (وحتى أربعة أرقام مهمة، فهو 1.000). وهكذا،\(n_1=1.00\) هنا. من المعلومات المعطاة،\(θ_1=30.0°\) و\(θ_2=22.0°\). باستخدام هذه المعلومات، فإن المجهول الوحيد في قانون سنيل هو\(n_2\)، لذلك يمكننا استخدام قانون سنيل (المعادلة\ ref {قانون snell}) للعثور عليه.

الحل

من قانون سنيل (المعادلة\ المرجع {قانون snell})، لدينا

\[\begin{align*} n_1\sin θ_1 &=n_2 \sin θ_2 \\[4pt] n_2 &= n_1\dfrac{\sin θ_1}{\sin θ_2}. \end{align*} \nonumber \]

إدخال القيم المعروفة،

\[\begin{align*} n_2 &=1.00 \dfrac{\sin 30.0°}{\sin 22.0°} \\[4pt] &= \dfrac{0.500}{0.375} \\[4pt] &=1.33. \end{align*} \nonumber \]

الدلالة

هذا هو معامل الانكسار للماء، وكان بإمكان سنيل تحديده من خلال قياس الزوايا وإجراء هذا الحساب. كان سيجد بعد ذلك أن 1.33 هو مؤشر الانكسار المناسب للماء في جميع الحالات الأخرى، مثل عندما يمر الشعاع من الماء إلى الزجاج. اليوم، يمكننا التحقق من أن معامل الانكسار مرتبط بسرعة الضوء في الوسط من خلال قياس تلك السرعة مباشرة.

استكشف انحناء الضوء بين وسيطين بمؤشرات انكسار مختلفة. استخدم محاكاة «المقدمة» وشاهد كيف يؤدي التغيير من الهواء إلى الماء إلى الزجاج إلى تغيير زاوية الانحناء. استخدم أداة المنقلة لقياس الزوايا ومعرفة ما إذا كان يمكنك إعادة إنشاء التكوين في المثال\(\PageIndex{1}\). أيضًا من خلال القياس، تأكد من أن زاوية الانعكاس تساوي زاوية السقوط.

مثال\(\PageIndex{2}\): A Larger Change in Direction

لنفترض أنه في مثل هذه الحالة في المثال\(\PageIndex{1}\)، ينتقل الضوء من الهواء إلى الماس وأن زاوية السقوط هي 30.0 درجة. احسب زاوية الانكسار ₂ في الماس.

إستراتيجية

مرة أخرى، يُؤخذ معامل الانكسار للهواء على أنه n ₁ =1.00، ونعطى ₁ =30.0°. يمكننا البحث عن معامل انكسار الماس، بإيجاد n ₂ =2.419. المجهول الوحيد في قانون سنيل هو\(θ_2\)، الذي نرغب في تحديده.

الحل

حل قانون سنيل (المعادلة\ المرجع {قانون snell})\(\sin θ_2\) للعوائد

\[\sin θ_2=\frac{n_1}{n_2}\sin θ_1. \nonumber \]

إدخال القيم المعروفة،

\[\sin θ_2=\frac{1.00}{2.419}\sin30.0°=(0.413)(0.500)=0.207. \nonumber \]

وبالتالي فإن الزاوية هي

\[θ_2=\sin^{−1}(0.207)=11.9°. \nonumber \]

الدلالة

بالنسبة لنفس زاوية السقوط البالغة 30.0 درجة، تكون زاوية الانكسار في الماس أصغر بكثير منها في الماء (11.9 درجة بدلاً من 22.0 درجة - انظر المثال\(\PageIndex{2}\)). هذا يعني أن هناك تغيرًا أكبر في اتجاه الماس. سبب التغيير الكبير في الاتجاه هو تغيير كبير في مؤشر الانكسار (أو السرعة). بشكل عام، كلما زاد التغيير في السرعة، زاد التأثير على اتجاه الشعاع.

التمارين\(\PageIndex{1}\): Zircon

المادة الصلبة ذات معامل الانكسار التالي الأعلى بعد الماس هي الزركون. إذا\(\PageIndex{2}\) تم استبدال الماس في المثال بقطعة من الزركون، فما زاوية الانكسار الجديدة؟

إجابة: 15.1 درجة