7.3: حل المشكلات
- Page ID
- 199583
يواجه الأشخاص مشاكل كل يوم - عادةً مشاكل متعددة على مدار اليوم. في بعض الأحيان تكون هذه المشاكل واضحة: لمضاعفة وصفة عجينة البيتزا، على سبيل المثال، كل ما هو مطلوب هو مضاعفة كل مكون في الوصفة. ومع ذلك، في بعض الأحيان، تكون المشاكل التي نواجهها أكثر تعقيدًا. على سبيل المثال، لنفترض أن لديك موعدًا نهائيًا للعمل، ويجب عليك إرسال نسخة مطبوعة من التقرير بالبريد إلى المشرف الخاص بك بحلول نهاية يوم العمل. التقرير حساس للوقت ويجب إرساله بين عشية وضحاها. لقد انتهيت من التقرير الليلة الماضية، لكن طابعتك لن تعمل اليوم. ماذا يجب أن تفعل؟ تحتاج أولاً إلى تحديد المشكلة ثم تطبيق استراتيجية لحل المشكلة.
استراتيجيات حل المشكلات
عندما تواجه مشكلة - سواء كانت مشكلة رياضية معقدة أو طابعة معطلة، كيف يمكنك حلها؟ قبل إيجاد حل للمشكلة، يجب أولاً تحديد المشكلة بوضوح. بعد ذلك، يمكن تطبيق واحدة من العديد من استراتيجيات حل المشكلات، ونأمل أن يؤدي ذلك إلى حل.
استراتيجية حل المشكلات هي خطة عمل تستخدم لإيجاد حل. الاستراتيجيات المختلفة لها خطط عمل مختلفة مرتبطة بها (الجدول 7.2). على سبيل المثال، الإستراتيجية المعروفة هي التجربة والخطأ. يصف القول المأثور القديم، «إذا لم تنجح في البداية، حاول، حاول مرة أخرى» التجربة والخطأ. فيما يتعلق بالطابعة المعطلة، يمكنك محاولة التحقق من مستويات الحبر، وإذا لم ينجح ذلك، يمكنك التحقق للتأكد من عدم انحشار درج الورق. أو ربما لم تكن الطابعة متصلة فعليًا بجهاز الكمبيوتر المحمول. عند استخدام التجربة والخطأ، ستستمر في تجربة حلول مختلفة حتى تحل مشكلتك. على الرغم من أن التجربة والخطأ ليست عادةً واحدة من أكثر الاستراتيجيات كفاءة من حيث الوقت، إلا أنها شائعة الاستخدام.
| استراتيجيات حل المشكلات | ||
|---|---|---|
| الأسلوب | وصف | مثال |
| التجربة والخطأ | استمر في تجربة حلول مختلفة حتى يتم حل المشكلة | إعادة تشغيل الهاتف وإيقاف تشغيل WiFi وإيقاف تشغيل البلوتوث لتحديد سبب خلل هاتفك |
| خوارزمية | صيغة حل المشكلات خطوة بخطوة | دليل التعليمات لتثبيت برنامج جديد على جهاز الكمبيوتر الخاص بك |
| الاستدلالية | إطار عام لحل المشكلات | العمل بشكل عكسي؛ تقسيم المهمة إلى خطوات |
نوع آخر من الإستراتيجية هو الخوارزمية. الخوارزمية هي صيغة لحل المشكلات توفر لك تعليمات خطوة بخطوة تستخدم لتحقيق النتيجة المرجوة (Kahneman، 2011). يمكنك التفكير في الخوارزمية كوصفة تحتوي على تعليمات مفصلة للغاية تنتج نفس النتيجة في كل مرة يتم فيها تنفيذها. تُستخدم الخوارزميات بشكل متكرر في حياتنا اليومية، خاصة في علوم الكمبيوتر. عند إجراء بحث على الإنترنت، تستخدم محركات البحث مثل Google الخوارزميات لتحديد الإدخالات التي ستظهر أولاً في قائمة النتائج. يستخدم Facebook أيضًا خوارزميات لتحديد المنشورات التي سيتم عرضها على ملف الأخبار الخاص بك. هل يمكنك تحديد الحالات الأخرى التي تستخدم فيها الخوارزميات؟
الاستدلال هو نوع آخر من استراتيجيات حل المشكلات. في حين أنه يجب اتباع الخوارزمية بالضبط لإنتاج نتيجة صحيحة، فإن التوجيه هو إطار عام لحل المشكلات (Tversky & Kahneman، 1974). يمكنك التفكير في هذه الأمور على أنها اختصارات ذهنية تُستخدم لحل المشكلات. «القاعدة العامة» هي مثال على الاستدلال. توفر هذه القاعدة الوقت والطاقة للشخص عند اتخاذ القرار، ولكن على الرغم من خصائصها الموفرة للوقت، إلا أنها ليست دائمًا أفضل طريقة لاتخاذ قرار عقلاني. تُستخدم أنواع مختلفة من الاستدلال في أنواع مختلفة من المواقف، ولكن الدافع لاستخدام الاستدلال يحدث عند استيفاء أحد الشروط الخمسة (Pratkanis، 1989):
يعد العمل بشكل عكسي طريقة إرشادية مفيدة تبدأ من خلالها في حل المشكلة من خلال التركيز على النتيجة النهائية. خذ بعين الاعتبار هذا المثال: أنت تعيش في واشنطن العاصمة وقد تمت دعوتك لحضور حفل زفاف في الساعة 4 مساءً يوم السبت في فيلادلفيا. مع العلم أن الطريق السريع 95 يميل إلى النسخ الاحتياطي في أي يوم من أيام الأسبوع، فأنت بحاجة إلى تخطيط مسارك ووقت مغادرتك وفقًا لذلك. إذا كنت تريد أن تكون في خدمة الزفاف بحلول الساعة 3:30 مساءً، واستغرق الأمر 2.5 ساعة للوصول إلى فيلادلفيا بدون حركة مرور، فما الوقت الذي يجب أن تغادر فيه منزلك؟ أنت تستخدم أسلوب العمل الرجعي لتخطيط أحداث يومك بشكل منتظم، ربما دون حتى التفكير في الأمر.
طريقة إرشادية مفيدة أخرى هي ممارسة تحقيق هدف أو مهمة كبيرة عن طريق تقسيمها إلى سلسلة من الخطوات الصغيرة. غالبًا ما يستخدم الطلاب هذه الطريقة الشائعة لإكمال مشروع بحثي كبير أو مقال طويل للمدرسة. على سبيل المثال، عادةً ما يقوم الطلاب بتبادل الأفكار، وتطوير أطروحة أو موضوع رئيسي، والبحث في الموضوع المختار، وتنظيم معلوماتهم في مخطط تفصيلي، وكتابة مسودة أولية، ومراجعة المسودة الأولية وتحريرها، وتطوير مسودة نهائية، وتنظيم قائمة المراجع، وتصحيح أعمالهم قبل تسليم المشروع. تصبح المهمة الكبيرة أقل صعوبة عندما يتم تقسيمها إلى سلسلة من الخطوات الصغيرة.
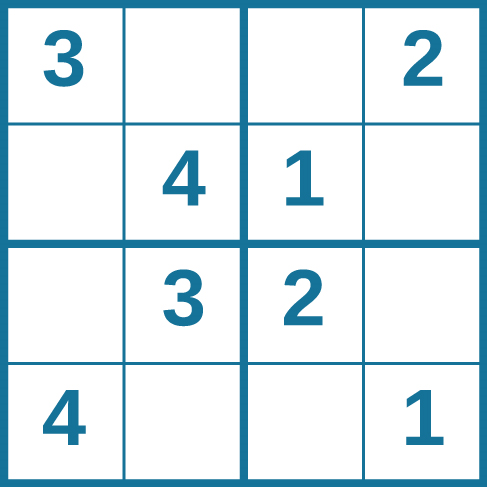
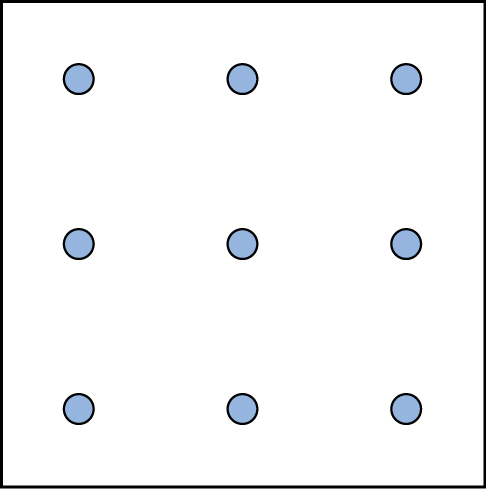
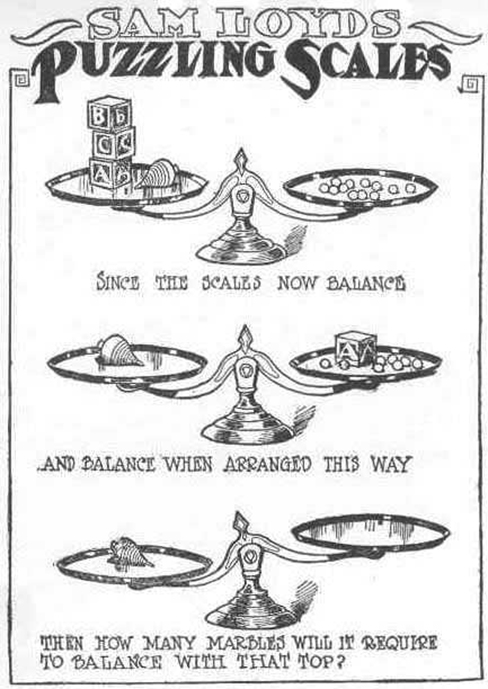
يمكن أن تتحسن قدرات حل المشكلات بالممارسة. يتحدى العديد من الأشخاص أنفسهم كل يوم بالألغاز والتمارين العقلية الأخرى لصقل مهاراتهم في حل المشكلات. تظهر ألغاز سودوكو يوميًا في معظم الصحف. عادةً ما تكون أحجية السودوكو عبارة عن شبكة 9 × 9. السودوكو البسيط أدناه (الشكل 7.7) عبارة عن شبكة 4 × 4. لحل اللغز، املأ المربعات الفارغة برقم واحد: 1 أو 2 أو 3 أو 4. فيما يلي القواعد: يجب أن يبلغ إجمالي الأرقام 10 في كل مربع غامق وكل صف وكل عمود؛ ومع ذلك، يمكن أن يظهر كل رقم مرة واحدة فقط في المربع الغامق والصف والعمود. حدد الوقت لنفسك أثناء حل هذا اللغز وقارن وقتك مع زميل في الفصل.
مزالق حل المشكلات
ومع ذلك، لا يتم حل جميع المشكلات بنجاح. ما هي التحديات التي تمنعنا من حل المشكلة بنجاح؟ قال ألبرت أينشتاين ذات مرة: «الجنون هو فعل الشيء نفسه مرارًا وتكرارًا وتوقع نتيجة مختلفة». تخيل شخصًا في غرفة بها أربعة أبواب. أحد المداخل التي كانت مفتوحة دائمًا في الماضي مغلق الآن. الشخص، الذي اعتاد على الخروج من الغرفة من هذا المدخل المحدد، يستمر في محاولة الخروج من نفس المدخل على الرغم من أن المداخل الثلاثة الأخرى مفتوحة. الشخص عالق - لكنها تحتاج فقط إلى الذهاب إلى مدخل آخر، بدلاً من محاولة الخروج من المدخل المغلق. المجموعة الذهنية هي المكان الذي تستمر فيه في التعامل مع المشكلة بطريقة نجحت في الماضي ولكن من الواضح أنها لا تعمل الآن.
الثبات الوظيفي هو نوع من المجموعة الذهنية حيث لا يمكنك إدراك كائن يستخدم لشيء آخر غير ما تم تصميمه من أجله. أجرى دانكر (1945) بحثًا تأسيسيًا حول الثبات الوظيفي. ابتكر تجربة تم فيها إعطاء المشاركين شمعة وكتاب أعواد الثقاب وعلبة من أصابع الإبهام. تم توجيههم لاستخدام هذه العناصر لربط الشمعة بالحائط حتى لا تقطر الشمع على الطاولة أدناه. كان على المشاركين استخدام الثبات الوظيفي لحل المشكلة (الشكل 7.10). خلال مهمة أبولو 13 إلى القمر، كان على مهندسي ناسا في Mission Control التغلب على الثبات الوظيفي لإنقاذ حياة رواد الفضاء على متن المركبة الفضائية. أدى انفجار في وحدة من المركبة الفضائية إلى إتلاف أنظمة متعددة. كان رواد الفضاء في خطر التعرض للتسمم بسبب ارتفاع مستويات ثاني أكسيد الكربون بسبب مشاكل في فلاتر ثاني أكسيد الكربون. وجد المهندسون طريقة لرواد الفضاء لاستخدام الأكياس البلاستيكية الاحتياطية والأشرطة وخراطيم الهواء لإنشاء فلتر هواء مؤقت أنقذ حياة رواد الفضاء.
لقد بحث الباحثون ما إذا كان الثبات الوظيفي يتأثر بالثقافة. في إحدى التجارب، طُلب من أفراد من مجموعة Shuar في الإكوادور استخدام كائن لغرض آخر غير الغرض الذي تم تصميم الكائن من أجله في الأصل. على سبيل المثال، تم إخبار المشاركين بقصة عن دب وأرنب يفصل بينهما نهر وطُلب منهم الاختيار من بين أشياء مختلفة، بما في ذلك الملعقة والكوب والممحاة وما إلى ذلك لمساعدة الحيوانات. كانت الملعقة هي الشيء الوحيد الذي يكفي لتمديد النهر الخيالي، ولكن إذا تم تقديم الملعقة بطريقة تعكس استخدامها العادي، فقد استغرق المشاركون وقتًا أطول لاختيار الملعقة لحل المشكلة. (جيرمان آند باريت، 2005). أراد الباحثون معرفة ما إذا كان التعرض لأدوات متخصصة للغاية، كما يحدث مع الأفراد في الدول الصناعية، يؤثر على قدرتهم على تجاوز الثبات الوظيفي. تم تحديد أن الثبات الوظيفي موجود في كل من الثقافات الصناعية وغير الصناعية (German & Barrett، 2005).
من أجل اتخاذ قرارات جيدة، نستخدم معرفتنا ومنطقنا. غالبًا ما تكون هذه المعرفة والمنطق سليمين ومتينًا. ومع ذلك، في بعض الأحيان، نتأثر بالتحيزات أو بتلاعب الآخرين بالموقف. على سبيل المثال، لنفترض أنك وثلاثة من أصدقائك أرادوا استئجار منزل وكان لديك ميزانية مستهدفة مجمعة تبلغ 1,600 دولار. يعرض لك السمسار منازل متهدمة للغاية مقابل 1,600 دولار فقط ثم يعرض لك منزلًا لطيفًا جدًا مقابل 2000 دولار. هل يمكنك أن تطلب من كل شخص دفع المزيد من الإيجار للحصول على منزل بقيمة 2000 دولار؟ لماذا سيُظهر لك السمسار المنازل المتهدمة والمنزل الجميل؟ قد يتحدى السمسار تحيزك الراسخ. يحدث التحيز الراسخ عندما تركز على معلومة واحدة عند اتخاذ قرار أو حل مشكلة. في هذه الحالة، تركز بشدة على مبلغ المال الذي ترغب في إنفاقه بحيث قد لا تتعرف على أنواع المنازل المتاحة عند نقطة السعر هذه.
تحيز التأكيد هو الميل إلى التركيز على المعلومات التي تؤكد معتقداتك الحالية. على سبيل المثال، إذا كنت تعتقد أن أستاذك ليس لطيفًا جدًا، فإنك تلاحظ جميع حالات السلوك الوقح التي أظهرها الأستاذ بينما تتجاهل التفاعلات الممتعة التي لا تعد ولا تحصى التي يشارك فيها يوميًا. يقودك التحيز بعد فوات الأوان إلى الاعتقاد بأن الحدث الذي مررت به للتو كان متوقعًا، على الرغم من أنه لم يكن كذلك حقًا، وبعبارة أخرى، كنت تعلم طوال الوقت أن الأمور ستسير بالطريقة التي حدثت بها. يصف التحيز التمثيلي طريقة تفكير خاطئة، حيث تقوم عن غير قصد بتصوير صورة نمطية لشخص أو شيء ما؛ على سبيل المثال، قد تفترض أن أساتذتك يقضون وقت فراغهم في قراءة الكتب والانخراط في محادثة فكرية، لأن فكرة قضاء وقتهم في اللعب لا تتناسب الكرة الطائرة أو زيارة مدينة الملاهي مع الصور النمطية للأساتذة.
أخيرًا، يعد التوافر الاستدلالي أسلوبًا استدلاليًا تتخذ فيه قرارًا بناءً على مثال أو معلومات أو تجربة حديثة متاحة لك بسهولة، على الرغم من أنها قد لا تكون أفضل مثال لإبلاغ قرارك. تميل التحيزات إلى «الحفاظ على ما هو موجود بالفعل - للحفاظ على معرفتنا ومعتقداتنا ومواقفنا وفرضياتنا الموجودة مسبقًا» (Aronson، 1995؛ Kahneman، 2011). يتم تلخيص هذه التحيزات في الجدول 7.3.
| ملخص تحيزات القرار | |
|---|---|
| انحياز | وصف |
| الإرساء | الميل إلى التركيز على معلومة معينة عند اتخاذ القرارات أو حل المشكلات |
| التأكيد | يركز على المعلومات التي تؤكد المعتقدات الموجودة |
| الإدراك المتأخر | الاعتقاد بأن الحدث الذي شهدته للتو كان متوقعًا |
| الممثل | تنميط غير مقصود لشخص أو شيء ما |
| التوافر | يعتمد القرار إما على سابقة متاحة أو مثال قد يكون خاطئًا |
شاهد هذا الفيديو الموسيقي الذي أعده المعلم حول التحيزات المعرفية لمعرفة المزيد.