17.5: الأنماط العادية للموجة الصوتية الدائمة
- Page ID
- 199823
- شرح الآلية وراء سماعات الرأس التي تعمل على تقليل الصوت
- وصف الرنين في أنبوب مغلق من أحد الطرفين ومفتوح من الطرف الآخر
- وصف الرنين في أنبوب مفتوح عند كلا الطرفين
التداخل هو السمة المميزة للموجات، وكلها تُظهر تداخلًا بناءً ومدمرًا مشابهًا تمامًا لما يحدث لموجات المياه. في الواقع، إحدى الطرق لإثبات شيء ما «هو موجة» هي مراقبة تأثيرات التداخل. نظرًا لأن الصوت عبارة عن موجة، فإننا نتوقع أن يظهر تداخلًا.
تداخل الموجات الصوتية
في الموجات، ناقشنا تداخل وظائف الموجة التي تختلف فقط في التحول الطوري. وجدنا أن دالة الموجة الناتجة عن تراكب\(y_{1}(x, t)=A \sin (k x-\omega t+\phi)\) و\(y_{2}(x, t)=A \sin (k x-\omega t)\) هي
\[ y(x, t)=\left[2 A \cos \left(\frac{\phi}{2}\right)\right] \sin \left(k x-\omega t+\frac{\phi}{2}\right). \nonumber \]
تتمثل إحدى طرق خروج موجتين متطابقتين في البداية من الطور مع بعضهما البعض في جعل الموجات تنتقل لمسافات مختلفة؛ أي أن لها أطوال مسارات مختلفة. توفر الموجات الصوتية مثالًا ممتازًا لتغيير الطور بسبب اختلاف المسار. كما ناقشنا، يمكن تصميم الموجات الصوتية أساسًا على شكل موجات طولية، حيث تتأرجح جزيئات الوسط حول موضع التوازن، أو كموجات ضغط.
عندما تغادر الموجات مكبرات الصوت، فإنها تخرج كموجات كروية (الشكل\(\PageIndex{1}\)). تتداخل الأمواج؛ وينتج الاستدلال البناء عن طريق الجمع بين قمتين أو حوضين، كما هو موضح. ينتج التداخل المدمر عن طريق الجمع بين الحوض الصغير والقمة.
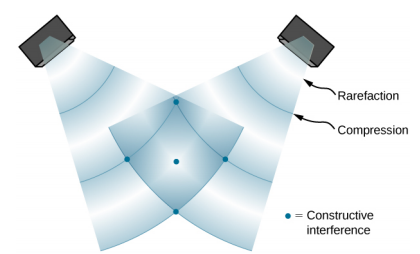
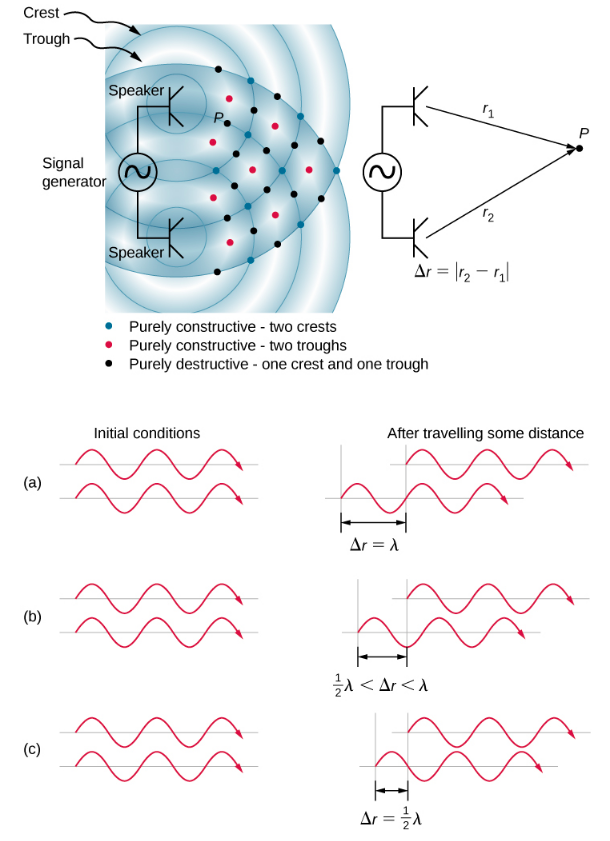
يرجع اختلاف الطور عند كل نقطة إلى أطوال المسارات المختلفة التي تقطعها كل موجة. عندما يكون الفرق في أطوال المسارات عددًا صحيحًا مضاعفًا لطول الموجة،
\[ \Delta r=\left|r_{2}-r_{1}\right|=n \lambda, \text { where } n=0,1,2,3, \ldots \nonumber \]
الأمواج في طور التكوين وهناك تداخل بناء. عندما يكون الفرق في أطوال المسارات مضاعفًا فرديًا لنصف الطول الموجي،
\[ \Delta r=\left|r_{2}-r_{1}\right|=n \frac{\lambda}{2}, \text { where } n=1,3,5, \ldots \nonumber \]
تكون الموجات خارج الطور بمقدار 180 درجة (\(\pi\)راد) والنتيجة هي التداخل المدمر. يمكن تحديد هذه النقاط باستخدام مقياس شدة مستوى الصوت.
يتم فصل مكبري صوت بمقدار 5.00 مترًا ويتم تشغيلهما بواسطة مولد إشارة بتردد غير معروف. يخرج طالب مزوَّد بجهاز قياس مستوى الصوت من مسافة ٦٫٠٠ م وينزل مسافة ٢٫٠٠ م، ويجد الحد الأدنى الأول للشدة، كما هو موضح أدناه. ما التردد الذي يوفره مولد الإشارة؟ افترض أن سرعة موجة الصوت هي v = 343.00m/s.
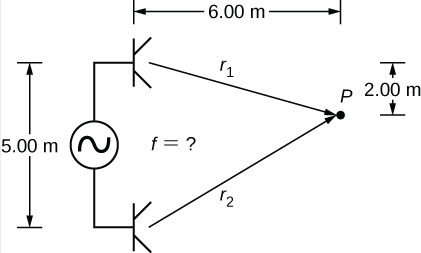
إستراتيجية
سرعة الموجة تساوي\(v = \frac{\lambda}{T} = \lambda f\). التردد هو إذن\(f = \frac{v}{\lambda}\). تشير الكثافة الدنيا إلى التداخل المدمر وتحدث النقطة الأولى من هذا القبيل عندما يكون هناك اختلاف في المسار يمكن العثور عليه من الهندسة.\(\Delta r = \lambda / 2\)
الحل
1. ابحث عن طول المسار إلى الحد الأدنى للنقطة من كل مكبر صوت
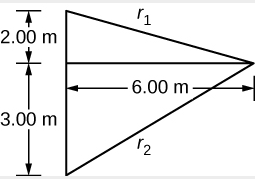
\[ r_{1}=\sqrt{(6.00 \: \mathrm{m})^{2}+(2.00 \: \mathrm{m})^{2}}=6.32 \: \mathrm{m}, r_{2}=\sqrt{(6.00 \: \mathrm{m})^{2}+(3.00 \: \mathrm{m})^{2}}=6.71 \: \mathrm{m} \nonumber \]
2. استخدم الفرق في طول المسار للعثور على الطول الموجي.
\ ابدأ {مصفوفة} {ج}
\ دلتا r=\ يسار |r_ {2} -r_ {1}\ يمين |=|=|6.71\:\ الرياضيات {م} -6.32\:\ الرياضيات {م} |=0.39\:\ الرياضيات {م}\\ لا يوجد رقم
\\\ لامبر=2\ دلتا r=2 (0.39\:\ ماثرم {}) =0.78\:\ الرياضيات {m}\ لا يوجد رقم
\ نهاية {مصفوفة}
3. ابحث عن التردد.
\[ f=\frac{v}{\lambda}=\frac{343.00 \: \mathrm{m} / \mathrm{s}}{0.78 \: \mathrm{m}}=439.74 \: \mathrm{Hz} \nonumber \]
الدلالة
إذا كانت النقطة P نقطة ذات كثافة قصوى، فسيكون طول المسار عددًا صحيحًا مضاعفًا لطول الموجة.
إذا كنت تتجول حول مكبري صوت لتشغيل الموسيقى، فكيف لا تلاحظ الأماكن التي تكون فيها الموسيقى صاخبة جدًا أو ناعمة جدًا، أي حيث يوجد تداخل بناء ومدمر؟
يعد مفهوم تغيير الطور بسبب الاختلاف في طول المسار مهمًا جدًا. ستستخدم هذا المفهوم مرة أخرى في التداخل والفوتونات وموجات المادة، حيث نناقش كيف استخدم توماس يونغ هذه الطريقة في تجربته الشهيرة ذات الشق المزدوج لتقديم دليل على أن الضوء له خصائص موجية.
تقليل الضوضاء من خلال التداخل المدمر
\(\PageIndex{3}\)يوضح الشكل استخدامًا ذكيًا لتداخل الصوت لإلغاء الضوضاء. تم اقتراح تطبيقات واسعة النطاق للحد النشط من الضوضاء عن طريق التداخل المدمر لمقصورات الركاب بأكملها في الطائرات التجارية. للحصول على تداخل مدمر، يتم إجراء تحليل إلكتروني سريع، ويتم إدخال صوت ثانٍ بزاوية 180 درجة خارج نطاق الصوت الأصلي، مع عكس الحد الأقصى والحد الأدنى تمامًا من الضوضاء الواردة. الموجات الصوتية في السوائل هي موجات ضغط وتتوافق مع مبدأ باسكال؛ أي أن الضغوط من مصدرين مختلفين تجمع وتطرح مثل الأرقام البسيطة. لذلك، تضيف ضغوط القياس الإيجابية والسلبية ضغطًا أصغر بكثير، مما ينتج صوتًا أقل كثافة. على الرغم من أن التداخل المدمر تمامًا ممكن فقط في أبسط الظروف، فمن الممكن تقليل مستويات الضوضاء بمقدار 30 ديسيبل أو أكثر باستخدام هذه التقنية.
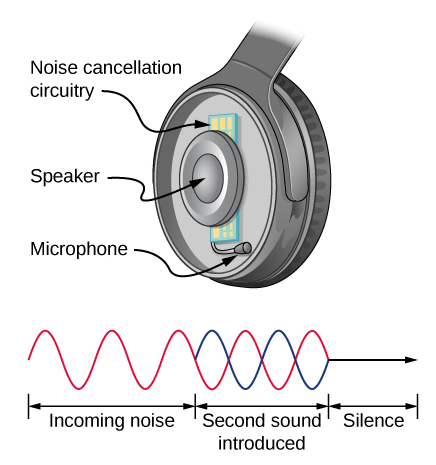
وصف كيف تختلف سماعات إلغاء الضوضاء عن سماعات الرأس القياسية المستخدمة لحجب الأصوات الخارجية.
في أي مكان آخر يمكننا ملاحظة تداخل الصوت؟ تعود جميع الأصداء الصوتية، كما هو الحال في الآلات الموسيقية، إلى التداخل البناء والمدمر. فقط الترددات الرنانة تتدخل بشكل بناء لتشكيل موجات دائمة، في حين أن البعض الآخر يتدخل بشكل مدمر ويغيب.
رنين في أنبوب مغلق عند أحد طرفيه
كما ناقشنا في Waves، تتكون الموجات الواقفة من موجتين تتحركان في اتجاهين متعاكسين. عندما تتحرك موجتان جيبيتان متطابقتان في اتجاهين متعاكسين، يمكن تصميم الموجات على النحو التالي
\[ y_{1}(x, t)=A \sin (k x-\omega t) \text { and } y_{2}(x, t)=A \sin (k x+\omega t) \nonumber .\]
عندما تتداخل هاتان الموجتان، تكون الموجة الناتجة موجة دائمة:
\[ y_{\mathrm{R}}(x, t)=[2 A \sin (k x)] \cos (\omega t) . \nonumber \]
يمكن إنتاج الرنين بسبب الشروط الحدودية المفروضة على الموجة. في Waves، أظهرنا أنه يمكن إنتاج الرنين في خيط تحت التوتر له ظروف حدودية متماثلة، وتحديدًا عقدة في كل طرف. لقد حددنا العقدة كنقطة ثابتة حيث لم تتحرك السلسلة. وجدنا أن ظروف الحدود المتماثلة أدت إلى رنين بعض الترددات وإنتاج موجات دائمة، بينما تتداخل الترددات الأخرى بشكل مدمر. يمكن أن يتردد صدى الموجات الصوتية في أنبوب مجوف، وتعتمد ترددات الموجات الصوتية التي يتردد صداها على الظروف الحدودية.
لنفترض أن لدينا أنبوبًا مغلقًا من أحد الطرفين ومفتوحًا من الطرف الآخر. إذا أمسكنا بشوكة رنانة اهتزازية بالقرب من الطرف المفتوح للأنبوب، تنتقل موجة صوتية ساقطة عبر الأنبوب وتنعكس عن الطرف المغلق. الصوت المنعكس له نفس التردد والطول الموجي للموجة الصوتية الساقطة، ولكنه يتحرك في الاتجاه المعاكس. في الطرف المغلق للأنبوب، لا تتمتع جزيئات الهواء بحرية تذكر في التذبذب، وتنشأ عقدة. في الطرف المفتوح، تكون الجزيئات حرة في الحركة، وعند التردد الصحيح، يحدث مضاد. على عكس ظروف الحدود المتماثلة للموجات الدائمة على الخيط، فإن الشروط الحدودية للأنبوب المفتوح من أحد الطرفين والمغلقة في الطرف الآخر غير متماثلة: عقدة في الطرف المغلق ومضاد مضاد في الطرف المفتوح.
إذا كانت شوكة الضبط تحتوي على التردد الصحيح تمامًا، فإن عمود الهواء في الأنبوب يتردد بصوت عالٍ، ولكن في معظم الترددات يهتز قليلاً جدًا. هذه الملاحظة تعني فقط أن العمود الهوائي يحتوي على ترددات طبيعية معينة فقط. ضع في اعتبارك أقل تردد يؤدي إلى رنين الأنبوب، مما ينتج عنه صوت مرتفع. ستكون هناك عقدة في الطرف المغلق ومضاد مضاد في الطرف المفتوح، كما هو موضح في الشكل\(\PageIndex{4}\).
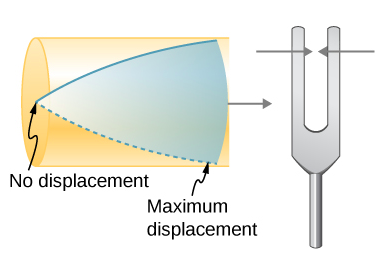
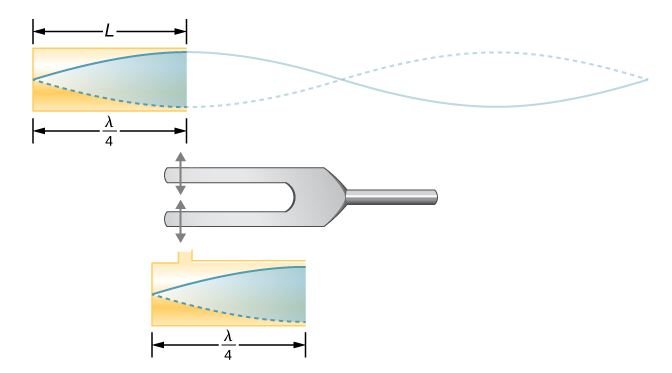
تحتوي الموجة الدائمة المتكونة في الأنبوب على مضاد في الطرف المفتوح وعقدة في الطرف المغلق. المسافة من العقدة إلى المضاد هي ربع الطول الموجي، وهذا يساوي طول الأنبوب؛ وهكذا،\(\lambda_1 = 4L\). يمكن إنتاج هذا الرنين نفسه عن طريق الاهتزاز الذي يتم إدخاله عند الطرف المغلق للأنبوب أو بالقرب منه (الشكل\(\PageIndex{5}\)). من الأفضل اعتبار هذا اهتزازًا طبيعيًا لعمود الهواء، بغض النظر عن كيفية حدوثه.
نظرًا لأن الحد الأقصى من عمليات إزاحة الهواء ممكن عند الطرف المفتوح ولا يمكن إزالته عند الطرف المغلق، فإن الأطوال الموجية الأقصر الأخرى يمكن أن يتردد صداها في الأنبوب، مثل تلك الموضحة في الشكل\(\PageIndex{6}\). هنا تحتوي الموجة الواقفة على ثلاثة أرباع طولها الموجي في الأنبوب\(\frac{3}{4} \lambda_3 = L\)، أو هكذا\(\lambda_3 = \frac{4}{3} L\). تكشف مواصلة هذه العملية عن سلسلة كاملة من الأصوات ذات الطول الموجي الأقصر والتردد العالي التي يتردد صداها في الأنبوب. نحن نستخدم مصطلحات محددة للأصداء في أي نظام. يُطلق على أدنى تردد رنين اسم الأساسي، بينما تسمى جميع ترددات الرنين العالية بإيحاءات. تسمى الترددات الرنانة التي تعد مضاعفات أساسية بشكل جماعي التوافقيات. الأساسي هو التوافقي الأول، التوافقي الثاني هو ضعف تردد التوافقي الأول، وهكذا. قد لا توجد بعض هذه التوافقيات لسيناريو معين. \(\PageIndex{7}\)يوضح الشكل الإيحاءات الأساسية والإيحاءات الثلاثة الأولى (أو التوافقيات الأولى والثالثة والخامسة والسابعة) في أنبوب مغلق في أحد طرفيه.
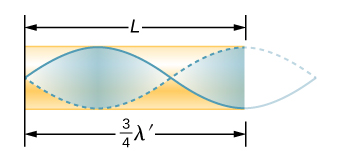
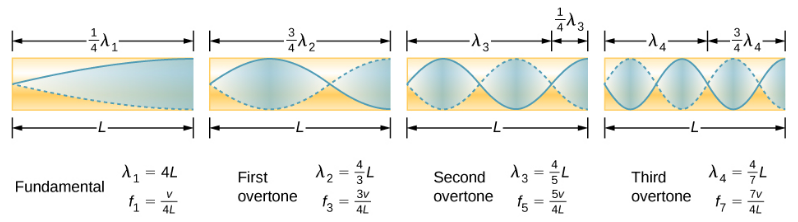
العلاقة بين الأطوال الموجية الرنانة للأنبوب المغلق عند أحد الطرفين هي
\[\lambda_{n}=\frac{4}{n} L \quad n=1,3,5, \ldots \label{17.13} \]
الآن دعونا نبحث عن نمط في ترددات الرنين لأنبوب بسيط مغلق من أحد طرفيه. يرتبط الحمض الأساسي\(\lambda = 4L\) والتردد بطول الموجة وسرعة الصوت كما هو موضح في
\[ v = f \lambda \nonumber .\]
يعطي حل العدد\(f\) في هذه المعادلة ما يلي:
\[ f=\frac{v}{\lambda}=\frac{v}{4 L}, \nonumber \]
حيث v هي سرعة الصوت في الهواء. وبالمثل، فإن النغمة الأولى لها\(\lambda = 4L/3\) (انظر الشكل\(\PageIndex{7}\))، بحيث
\[ f_{3}=3 \frac{v}{4 L}=3 f_{1} . \nonumber \]
لأننا\(f_3 = 3 f_1\) نسمي النغمة الأولى بالتناسق الثالث. استمرارًا لهذه العملية، نرى نمطًا يمكن تعميمه في تعبير واحد. الترددات الرنانة للأنبوب المغلق في أحد طرفيه هي
\[ f_{n}=n \frac{v}{4 L}, \quad n=1,3,5, \dots \label{17.14} \]
أين\(f_1\) هي الأساسية،\(f_3\) هي النغمة الأولى، وما إلى ذلك. من المثير للاهتمام أن ترددات الرنين تعتمد على سرعة الصوت وبالتالي على درجة الحرارة. يشكل هذا الاعتماد مشكلة ملحوظة للأعضاء في الكاتدرائيات القديمة غير المدفأة، وهو أيضًا السبب الذي يجعل الموسيقيين يجلبون آلات الرياح الخاصة بهم إلى درجة حرارة الغرفة قبل العزف عليها.
رنين في أنبوب مفتوح عند كلا الطرفين
مصدر آخر للموجات الراكدة هو الأنبوب المفتوح من كلا الطرفين. في هذه الحالة، تكون الشروط الحدودية متماثلة: مضاد في كل طرف. يمكن تحليل رنين الأنابيب المفتوحة من كلا الطرفين بطريقة مشابهة جدًا لتلك الخاصة بالأنابيب المغلقة في أحد الطرفين. تحتوي أعمدة الهواء في الأنابيب المفتوحة عند كلا الطرفين على الحد الأقصى من عمليات إزاحة الهواء عند كلا الطرفين (الشكل\(\PageIndex{8}\)). تتشكل الموجات الدائمة كما هو موضح.
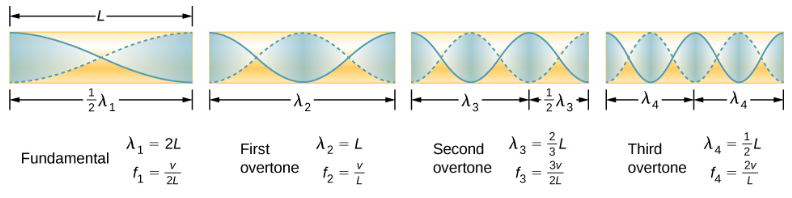
العلاقة بين الأطوال الموجية الرنانة للأنبوب المفتوح عند كلا الطرفين هي
\[ \lambda_{n}=\frac{2}{n} L, \quad n=1,2,3, \ldots \label{17.15} \]
استنادًا إلى حقيقة أن الأنبوب المفتوح في كلا الطرفين يحتوي على الحد الأقصى من عمليات إزاحة الهواء عند كلا الطرفين، وباستخدام الشكل\(\PageIndex{8}\) كدليل، يمكننا أن نرى أن ترددات الرنين للأنبوب المفتوح في كلا الطرفين هي
\[ f_{n}=n \frac{v}{2 L}, \quad n=1,2,3 \dots, \label{17.16} \]
أين\(f_1\) هي الأساسية،\(f_2\) هي النغمة الأولى،\(f_3\) هي النغمة الثانية، وهكذا. لاحظ أن الأنبوب المفتوح من كلا الطرفين له تردد أساسي ضعف ما سيكون عليه إذا تم إغلاقه من أحد الطرفين. كما أن لها طيفًا مختلفًا من الإيحاءات عن الأنبوب المغلق في أحد طرفيه.
لاحظ أن الأنبوب المفتوح من كلا الطرفين له شروط حدودية متماثلة، على غرار السلسلة المثبتة في كلا الطرفين التي تمت مناقشتها في Waves. العلاقات بين الأطوال الموجية والترددات للأداة الوترية هي نفسها كما هو موضح في المعادلة\ ref {17.15} والمعادلة\ ref {17.16}. سرعة الموجة على السلسلة (من Waves) هي\(v = \sqrt{\frac{F_{T}}{\mu}}\). يهتز الهواء المحيط بالخيط بنفس تردد الوتر، مما ينتج صوتًا بنفس التردد. تتحرك الموجة الصوتية بسرعة الصوت ويمكن العثور على الطول الموجي باستخدام\(v = \lambda f\).
كيف يمكن استخدام عقدة الموجة الدائمة والمضادة لتحديد طول الأنبوب المغلق
يتيح لك هذا الفيديو تصور الموجات الصوتية.
تلاحظ آلتين موسيقيتين لا يمكنك التعرف عليهما. أحدهما يعزف أصواتًا عالية النبرة والآخر يعزف أصواتًا منخفضة النبرة. كيف يمكنك تحديد أيهما دون سماع أي منهما يلعب؟


