17.4: كثافة الصوت

Last updated
Save as PDF

Page ID: 199829

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

تعريف مصطلح الكثافة
شرح مفهوم مستوى شدة الصوت
وصف كيفية ترجمة الأذن البشرية للصوت

في غابة هادئة، يمكنك أحيانًا سماع ورقة واحدة تسقط على الأرض. ولكن عندما يقوم سائق سيارة عابر بتشغيل جهاز الاستريو الخاص به، لا يمكنك حتى سماع ما يقوله الشخص المجاور لك في سيارتك (الشكل$\PageIndex{1}$). نحن جميعًا على دراية كبيرة بصوت الأصوات وندرك أن ارتفاع الصوت مرتبط بمدى قوة اهتزاز المصدر. يعد التعرض العالي للضوضاء خطرًا على السمع، ولهذا السبب من المهم للأشخاص الذين يعملون في البيئات الصناعية ارتداء واقي الأذن. الكمية المادية ذات الصلة هي شدة الصوت، وهو مفهوم صالح لجميع الأصوات سواء كانت في النطاق المسموع أم لا.

تظهر الصورة طريقًا مزدحمًا بالسيارات والدراجات النارية في دلهي. — الشكل$\PageIndex{1}$: الضوضاء على الطرق المزدحمة، مثل هذه في دلهي، تجعل من الصعب سماع الآخرين ما لم يصرخوا. (مصدر الصورة: «لينغاراج جي جي» /فليكر)

في السابق، قمنا بتعريف الكثافة على أنها الطاقة لكل وحدة مساحة تحملها الموجة. الطاقة هي معدل نقل الطاقة بواسطة الموجة. في شكل المعادلة، الكثافة$I$ هي

\[I = \frac{P}{A}, \label{17.8}\]

$P$أين الطاقة عبر المنطقة$A$. وحدة SI لـ$I$ هي W/m ². إذا افترضنا أن الموجة الصوتية كروية، وأنه لا يتم فقدان أي طاقة للعمليات الحرارية، فإن طاقة الموجة الصوتية تنتشر على مساحة أكبر مع زيادة المسافة، وبالتالي تنخفض الكثافة. مساحة الكرة هي$A = 4 \pi r^2$. عندما تنتشر الموجة من$r_1$ إلى$r_2$، تنتشر الطاقة أيضًا على مساحة أكبر:

\[\begin{align} P_{1} & = P_{2} \\[4pt] I_{1} 4 \pi r_{1}^{2} & = I_{2} 4 \pi r_{2}^{2} \\[4pt] I_{2} &= I_{1} \left(\dfrac{r_{1}}{r_{2}}\right)^{2} \ldotp \label{17.9} \end{align}\]

تنخفض الكثافة مع خروج الموجة من المصدر. في علاقة التربيعية العكسية، مثل الكثافة، عندما تضاعف المسافة، تنخفض الكثافة إلى الربع،

\[I_{2} = I_{1} \left(\dfrac{r_{1}}{r_{2}}\right)^{2} = I_{1} \left(\dfrac{r_{1}}{2r_{1}}\right)^{2} = \frac{1}{4} I_{1} \ldotp\]

بشكل عام، عند النظر في شدة الموجة الصوتية، نعتبر الكثافة هي القيمة المتوسطة للوقت للطاقة، المشار إليها بـ$⟨P⟩$، مقسومًا على المنطقة،

\[I = \frac{\langle P \rangle}{A} \ldotp \label{17.10}\]

تتناسب شدة الموجة الصوتية مع التغير في مربع الضغط وتتناسب عكسياً مع الكثافة والسرعة. ضع في اعتبارك طردًا من وسيط لم يتم إزعاجه في البداية ثم تأثره بموجة صوتية في الوقت t، كما هو موضح في الشكل$\PageIndex{2}$.

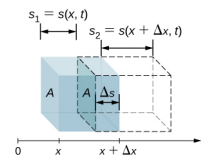
الصورة عبارة عن رسم لطرد من وسيط لم يتم إزعاجه في البداية ثم يتأثر بموجة صوتية. تتحرك موجة صوتية عبر الوسيط في الوقت t، ويتم تهجير الطرد وتوسيعه في اتجاه الإزاحة. — الشكل$\PageIndex{2}$: طرد غير مضطرب من وسيط بحجم$V = A \Delta x$ موضح باللون الأزرق. تتحرك موجة صوتية عبر الوسيط في الوقت المناسب$t$، ويتم تهجير الطرد وتوسيعه، كما هو موضح في الخطوط المنقطة. التغيير في الحجم هو$\Delta V = A \Delta s = A(s_2 − s_1)$، أين$s_1$ يتم إزاحة الحافة الأمامية للطرد$s_2$ وهو إزاحة الحافة الخلفية للطرد. في الشكل،$s_2 > s_1$ يتم توسيع الطرد، ولكن يمكن للطرد إما أن يتوسع أو يضغط ($s_2 < s_1$)، اعتمادًا على أي جزء من الموجة الصوتية (الضغط أو التراجع) يتحرك عبر الطرد.

عندما تتحرك الموجة الصوتية عبر الطرد، يتم تهجير الطرد وقد يتوسع أو يتقلص. إذا$s_2 > s_1$ زاد مستوى الصوت وانخفض الضغط. إذا$s_2 < s_1,$ انخفض مستوى الصوت وزاد الضغط. التغيير في مستوى الصوت هو

\[\begin{align} \Delta V &= A \Delta s \\[4pt] &= A(s_{2} - s_{1}) \\[4pt] &= A[s(x + \Delta x,t)-s(x,t)] \ldotp \end{align}\]

التغيير الجزئي في المجلد هو التغيير في الحجم مقسومًا على المجلد الأصلي:

\[ \begin{align} \frac{dV}{V} &= \lim_{\Delta x \rightarrow 0} \frac{A[s(x + \Delta x,t)-s(x,t)]}{A \Delta x} \\[4pt] &= \frac{\partial s(x,t)}{\partial x} \ldotp \end{align}\]

يرتبط التغيير الجزئي في الحجم بتقلب الضغط بمعامل الكتلة

\[\beta = − \frac{\Delta p(x, t)}{\frac{dV}{V}}.\]

تذكر أن علامة الطرح مطلوبة لأن مستوى الصوت مرتبط عكسيًا بالضغط. (نستخدم الأحرف الصغيرة للضغط$p$ لتمييزها عن الطاقة، المشار إليها بـ$P$.) وبالتالي فإن التغيير في الضغط هو

\[\Delta p(x, t) = − \beta \frac{dV}{V} = − \beta \frac{\partial s(x, t)}{\partial x}.\]

إذا كانت الموجة الصوتية جيبية، فإن الإزاحة كما هو موضح في المعادلة 17.2 هي

\[s(x, t) = s_{max} \cos(kx ∓ \omega t + \phi)\]

ووجد أن الضغط هو

\[ \begin{align} \Delta p(x,t) &= - \beta \frac{dV}{V} \\[4pt] &= - \beta \frac{\partial s(x,t)}{\partial x} \\[4pt] &= \beta ks_{max} \sin (kx - \omega t + \phi) \\[4pt] &= \Delta p_{max} \sin (kx - \omega t + \phi) \ldotp \end{align}\]

شدة الموجة الصوتية هي الطاقة لكل وحدة مساحة، والقوة هي القوة مضروبة في السرعة،

\[I = \frac{P}{A} = \frac{Fv}{A} = pv.\]

هنا، السرعة هي سرعة تذبذبات الوسط، وليس سرعة الموجة الصوتية. سرعة الوسيط هي المعدل الزمني للتغير في الإزاحة:

\[v(x,t) = \frac{\partial}{\partial y} s(x,t) = \frac{\partial}{\partial y} [s_{max} \cos (kx - \omega t + \phi)] = s_{max} \omega \sin (kx - \omega t + \phi) \ldotp\]

وهكذا تصبح الكثافة

\[\begin{align} I & = \Delta p(x,t)\; v(x,t) \\[4pt] & = \beta ks_{max} \sin (kx - \omega t + \phi)[s_{max} \omega \sin (kx - \omega t + \phi)] \\[4pt] & = \beta k \omega s_{max}^{2} \sin^{2} (kx - \omega t + \phi) \ldotp \end{align}\]

للعثور على متوسط الكثافة الزمنية خلال فترة واحدة$T = \frac{2 \pi}{\omega}$ للمركز$x$، ندمج على مدار الفترة،

\[I = \frac{\beta k \omega s_{max}^{2}}{2}.\]

باستخدام$\Delta p_{max} = \beta ks_{max}$$v = \sqrt{\frac{\beta}{\rho}}$، و$v = \frac{\omega}{k}$، نحصل عليه

\[ \begin{align*} I &= \frac{\beta k \omega s_{max}^{2}}{2} \\[4pt] &= \frac{\beta^{2} k^{2} \omega s_{max}^{2}}{2 \beta k} \\[4pt] &= \frac{\omega (\Delta p_{max})^{2}}{2 (\rho v^{2}) k} \\[4pt] &= \frac{v (\Delta p_{max})^{2}}{2 (\rho v^{2})} \\[4pt] &= \frac{(\Delta p_{max})^{2}}{2 \rho v} \ldotp \end{align*}\]

أي أن شدة الموجة الصوتية مرتبطة بسعتها المربعة

\[I = \frac{(\Delta p_{max})^{2}}{2 \rho v} \ldotp \label{17.11}\]

هنا،$\Delta$ الحد _الأقصى هو تغير الضغط أو سعة الضغط بوحدات باسكال (Pa) أو N/m ². تتناسب الطاقة (كطاقة حركية$\frac{1}{2} mv^2$) لعنصر متذبذب من الهواء بسبب موجة صوتية متحركة مع مربع اتساعه. في هذه المعادلة،$\rho$ هي كثافة المادة التي تنتقل فيها الموجة الصوتية، بوحدات كجم/م ³، وسرعة$v$ الصوت في الوسط، بوحدات م/ث، ويكون تغير الضغط متناسبًا مع سعة التذبذب، لذلك يتغير$I$ كـ ($\Delta p)^2$. تتوافق هذه العلاقة مع حقيقة أن الموجة الصوتية تنتج عن بعض الاهتزازات؛ فكلما زادت سعة ضغطها، زاد ضغط الهواء في الصوت الذي تنتجه.

مستويات السمع البشري وكثافة الصوت

كما ذكرنا سابقًا في هذا الفصل، السمع هو إدراك الصوت. تتضمن آلية السمع بعض الفيزياء المثيرة للاهتمام. الموجة الصوتية التي تصطدم بأذننا هي موجة ضغط. الأذن عبارة عن محول طاقة يحول الموجات الصوتية إلى نبضات عصبية كهربائية بطريقة أكثر تعقيدًا بكثير من الميكروفون ولكنها مماثلة له. $\PageIndex{3}$يوضح الشكل تشريح الأذن.

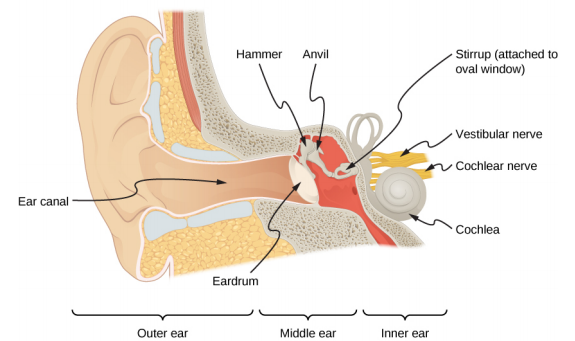
الصورة عبارة عن رسم لأذن. يُظهر انتهاء قناة الأذن بطبلة الأذن. تكون المطرقة المتصلة بالسندان في اتصال مع طبلة الأذن. خلف طبلة الأذن توجد المطرقة والسندان. السندان متصل بالركاب المتصل بالنافذة البيضاوية. تتلامس قوقعة الأذن والعصب القوقعي والعصب الدهليزي مع الرِكاب. — الشكل$\PageIndex{3}$: تشريح الأذن البشرية.

تنقل الأذن الخارجية، أو قناة الأذن، الصوت إلى طبلة الأذن المريحة والمحمية. يتردد صدى عمود الهواء في قناة الأذن وهو مسؤول جزئيًا عن حساسية الأذن للأصوات في نطاق 2000-5000-Hz. تقوم الأذن الوسطى بتحويل الصوت إلى اهتزازات ميكانيكية وتطبيق هذه الاهتزازات على القوقعة.

شاهد هذا الفيديو للحصول على مناقشة أكثر تفصيلاً لعمل الأذن البشرية.

يعتمد نطاق الشدة التي يمكن أن تسمعها الأذن البشرية على تردد الصوت، ولكن بشكل عام، النطاق كبير جدًا. الحد الأدنى لشدة العتبة التي يمكن سماعها هو I ₀ = 10 ⁻¹² W/m ². يتم الشعور بالألم عند شدة _الألم I = 1 W/m ². تعتبر قياسات شدة الصوت (بوحدات W/m ²) مرهقة للغاية بسبب هذا النطاق الكبير في القيم. لهذا السبب، وكذلك لأسباب أخرى، تم اقتراح مفهوم مستوى شدة الصوت.

يُعرَّف مستوى$\beta$ شدة الصوت، الذي يُقاس بالديسيبل، بكثافة I بالوات لكل متر مربع، على أنه

\[\beta (dB) = \log_{10} \left(\dfrac{I}{I_{0}}\right), \label{17.12}\]

حيث I ₀ = 10 ⁻¹² W/m ² هي شدة مرجعية تقابل الحد الأدنى لشدة الصوت التي يمكن للشخص ذو السمع العادي إدراكها بتردد 1.00 كيلو هرتز. من الشائع مراعاة مستويات شدة الصوت بالديسيبل مقارنة بـ W/m ². يمكن وصف كيفية إدراك آذان الإنسان للصوت بدقة أكبر من خلال لوغاريتم الشدة وليس بشكل مباشر من خلال الكثافة. نظرًا لأن β يتم تعريفها من حيث النسبة، فهي كمية بدون وحدة، تخبرك بمستوى الصوت بالنسبة إلى معيار ثابت (10 ⁻¹² واط/م ²). تُستخدم وحدات الديسيبل (dB) للإشارة إلى أن هذه النسبة مضروبة في 10 في تعريفها. تم تسمية الجرس، الذي يستند إليه الديسيبل، باسم ألكسندر جراهام بيل، مخترع الهاتف. مستوى الديسيبل للصوت الذي تبلغ شدته الحدية 10 ⁻¹² واط/م ² هو$\beta$ = 0 ديسيبل، لأن اللوغاريتم ₁₀ 1 = 0. $\PageIndex{2}$يعطي الجدول مستويات بالديسيبل والشدة بالواط لكل متر مربع لبعض الأصوات المألوفة. تكون الأذن حساسة لأقل من تريليون واط لكل متر مربع - وهذا أكثر إثارة للإعجاب عندما تدرك أن مساحة طبلة الأذن تبلغ حوالي 1 سم ² فقط، بحيث لا تسقط عليها سوى 10 ⁻¹⁶ واط عند عتبة السمع. تهتز جزيئات الهواء في موجة صوتية بهذه الكثافة على مسافة أقل من قطر جزيئي واحد، وتكون ضغوط القياس المعنية أقل من 10 ^{−9 atm}.

الجدول$\PageIndex{2}$: مستويات شدة الصوت وكثافته
مستوى شدة الصوت$\beta$ (ديسيبل)	الكثافة	مثال/تأثير
\ (\ بيتا\) (ديسيبل) ">0	1 × 10 ⁻¹²	عتبة السمع عند 1000 هرتز
\ (\ بيتا\) (ديسيبل) ">10	1 × 10 ⁻¹¹	حفيف الأوراق
\ (\ بيتا\) (ديسيبل) ">20	1 × 10 ⁻¹⁰	اهمس على مسافة 1 متر
\ (\ بيتا\) (ديسيبل) ">30	1 × 10 ⁻⁹	منزل هادئ
\ (\ بيتا\) (ديسيبل) ">40	1 × 10 ⁻⁸	منزل متوسط
\ (\ بيتا\) (ديسيبل) ">50	1 × 10 ⁻⁷	مكتب متوسط، موسيقى هادئة
\ (\ بيتا\) (ديسيبل) ">60	1 × 10 ⁻⁶	محادثة عادية
\ (\ بيتا\) (ديسيبل) ">70	1 × 10 ⁻⁵	مكتب صاخب وحركة مرور مزدحمة
\ (\ بيتا\) (ديسيبل) ">80	1 × 10 ⁻⁴	راديو صاخب، محاضرة في الفصل الدراسي
\ (\ بيتا\) (ديسيبل) ">90	1 × 10 ⁻³	داخل شاحنة ثقيلة؛ الأضرار الناجمة عن التعرض الطويل [1]
\ (\ بيتا\) (ديسيبل) ">100	1 × 10 ⁻²	مصنع صاخب، صفارة إنذار على ارتفاع 30 مترًا؛ التلف الناتج عن التعرض لمدة 8 ساعات يوميًا
\ (\ بيتا\) (ديسيبل) ">110	1 × 10 ⁻¹	الضرر الناتج عن التعرض لمدة 30 دقيقة يوميًا
\ (\ بيتا\) (ديسيبل) ">120	1	حفلة موسيقى الروك الصاخبة؛ آلة تقطيع تعمل بالهواء المضغوط على ارتفاع 2 متر؛ عتبة الألم
\ (\ بيتا\) (ديسيبل) ">140	1 × 10 ²	طائرة نفاثة على بعد 30 مترًا؛ ألم شديد وتلف في ثوانٍ
\ (\ بيتا\) (ديسيبل) ">160	1 × 10 ⁴	انفجار طبلة الأذن

[1] توصي العديد من الوكالات الحكومية والجمعيات المهنية ذات الصلة بالصحة بعدم تجاوز 85 ديسيبل للتعرض اليومي لمدة 8 ساعات في غياب حماية السمع.

الملاحظة التي تم التحقق منها بسهولة من خلال فحص الجدول$\PageIndex{2}$ أو باستخدام المعادلة\ ref {17.12} هي أن كل عامل من 10 في الكثافة يتوافق مع 10 ديسيبل. على سبيل المثال، يكون الصوت الذي يبلغ 90 ديسيبل مقارنة بصوت 60 ديسيبل أكبر بمقدار 30 ديسيبل، أو ثلاثة عوامل بقوة 10 (^{أي 10 3} مرات). مثال آخر هو أنه إذا كان أحد الأصوات بقوة 10 ⁷ مثل صوت آخر، فسيكون أعلى بمقدار 70 ديسيبل (الجدول$\PageIndex{2}$).

جدول$\PageIndex{2}$: نسب الشدة والاختلافات المقابلة في مستويات كثافة الصوت
$\frac{I_{2}}{I_{1}}$	$\beta_{2} - \beta_{1}$
\ (\ frac {I_ {2}} {I_ {1}}\)» النمط= محاذاة رأسية: متوسطة؛ ">2.0	\ (\ beta_ {2} -\ beta_ {1}\)» النمط = محاذاة رأسية: متوسطة؛ ">3.0 ديسيبل
\ (\ frac {I_ {2}} {I_ {1}}\)» النمط= محاذاة رأسية: متوسطة؛ ">5.0	\ (\ beta_ {2} -\ beta_ {1}\)» النمط = محاذاة رأسية: متوسطة؛ ">7.0 ديسيبل
\ (\ frac {I_ {2}} {I_ {1}}\)» النمط= المحاذاة الرأسية: الوسطى؛ ">10.0	\ (\ beta_ {2} -\ beta_ {1}\)» النمط = محاذاة رأسية: متوسطة؛ ">10.0 ديسيبل
\ (\ frac {I_ {2}} {I_ {1}}\)» النمط= المحاذاة الرأسية: الوسطى؛ ">100.0	\ (\ beta_ {2} -\ beta_ {1}\)» النمط = محاذاة رأسية: متوسطة؛ ">20.0 ديسيبل
\ (\ frac {I_ {2}} {I_ {1}}\)» النمط= المحاذاة الرأسية: الوسطى؛ ">1000.0	\ (\ beta_ {2} -\ beta_ {1}\)» النمط = محاذاة رأسية: متوسطة؛ ">30.0 ديسيبل

مثال$\PageIndex{1A}$: Calculating Sound Intensity Levels

احسب مستوى شدة الصوت بالديسيبل لموجة صوتية تنتقل في الهواء عند درجة حرارة 0 درجة مئوية وسعة ضغط مقدارها 0.656 باسكال.

إستراتيجية

لقد تم إعطاؤنا$Δp$، حتى نتمكن من الحساب$I$ باستخدام المعادلة

\[I = \dfrac{(\Delta p)^2}{2 \rho vw}.\]

باستخدام$I$، يمكننا الحساب$\beta$ مباشرة من تعريفه في

\[\beta (dB) = 10 \log_{10} \left(\dfrac{I}{I_{0}}\right).\]

الحل

حدد الأشياء المعروفة: ينتقل الصوت بسرعة 331 متر/ثانية في الهواء عند درجة حرارة 0 درجة مئوية، وتبلغ كثافة الهواء 1.29 كجم/م ³ عند الضغط الجوي و0 درجة مئوية.
أدخل هذه القيم وسعة الضغط في I =$\frac{(\Delta p)^{2}}{2 \rho v}$. $I =\ frac {(\ دلتا p) ^ {2}} {2\ rho v} =\ frac {(0.656\؛ باسكال) ^ {2}} {2} (1.29\؛ كغم/م^ {3}) (331\؛ م/ثانية)} = 5.04\ مرات 10^ {-4}\\\؛ W/m^ {2}\ ldotp $$
أدخل القيمة لـ I والقيمة المعروفة لـ I ₀ إلى$\beta$ (dB) = 10 log ₁₀$\left(\dfrac{I}{I_{0}}\right)$. احسب للعثور على مستوى شدة الصوت بالديسيبل: $10\ log_ {10} (5.04\ مرات 10^ {8}) = (10\؛ ديسيبل) (8.70) = 87\؛ dB\ ldotP$$

الأهمية

هذا الصوت ذو 87 ديسيبل له كثافة خمسة أضعاف صوت 80 ديسيبل. لذا فإن عامل خمسة في الكثافة يتوافق مع اختلاف 7 ديسيبل في مستوى شدة الصوت. هذه القيمة صحيحة لأي شدة تختلف بعامل خمسة.

مثال$\PageIndex{1B}$: Changing Intensity Levels of a Sound

أظهر أنه إذا كان أحد الأصوات أقوى بمرتين من صوت آخر، فسيكون مستوى الصوت أعلى بحوالي 3 ديسيبل.

إستراتيجية

يُقال لنا أن نسبة شدتي الشدة هي 2 إلى 1، ثم يُطلب منا إيجاد الفرق في مستويات الصوت بالديسيبل. يمكننا حل هذه المشكلة باستخدام خصائص اللوغاريتمات.

الحل

تحديد الأشياء المعروفة: نسبة الكثافتين هي 2 إلى 1، أو $$\ frac {I_ {2}} {I_ {1}} = 2.00\ lDotP$نود أن نوضح أن الفرق في مستويات الصوت هو حوالي 3 ديسيبل. أي أننا نريد أن نعرض: $$\ beta_ {2} -\ beta_ {1} = 3\؛ dB\ lDotP$$لاحظ أن $log_ {10} b -\ log_ {10} a =\ log_ {10}\ اليسار (\ dfrac {b} {a}\ اليمين)\ ldotp$$
استخدم تعريف الحصول على $$\ beta_ {2} -\ beta_ {1} = 10\ log_ {10}\ يسار (\ dfrac {I_ {2}}} {I_ {1}}\ يمين) = 10\ log_ {10} 2.00 = (10\؛ ديسيبل) (0.301)\ lDotP$$وهكذا، $\ beta_ {2} -\ beta_ {1} = 3.01\؛ ديسيبل\ ldot$$$\beta$

الأهمية

هذا يعني أن مستويي شدة الصوت يختلفان بمقدار 3.01 ديسيبل، أو حوالي 3 ديسيبل، كما هو معلن. لاحظ أنه بسبب إعطاء$\frac{I_{2}}{I_{1}}$ النسبة فقط (وليس الكثافة الفعلية)، فإن هذه النتيجة صحيحة لأي شدة تختلف بعامل اثنين. على سبيل المثال، يكون الصوت 56.0-dB ضعف كثافة الصوت الذي يبلغ 53.0 ديسيبل، ويكون الصوت 97.0-dB نصف كثافة صوت 100 ديسيبل، وهكذا.

التمارين$\PageIndex{1}$

حدد الأصوات الشائعة عند مستويات 10 ديسيبل و50 ديسيبل و100 ديسيبل.

يتم استخدام مقياس ديسيبل آخر أيضًا، يسمى مستوى ضغط الصوت، استنادًا إلى نسبة سعة الضغط إلى الضغط المرجعي. يستخدم هذا المقياس بشكل خاص في التطبيقات التي ينتقل فيها الصوت في الماء. إن معالجة هذا المقياس خارج نطاق هذا النص لأنه لا يُستخدم بشكل شائع للأصوات في الهواء، ولكن من المهم ملاحظة أنه قد تتم مصادفة مستويات ديسيبل مختلفة جدًا عند تحديد مستويات ضغط الصوت.

السمع والنبرة

تتمتع الأذن البشرية بنطاق وحساسية هائلين. يمكن أن يوفر لنا ثروة من المعلومات البسيطة - مثل درجة الصوت والجهارة والتوجيه.

يُطلق على مفهوم التردد اسم درجة الصوت. عادةً ما يتمتع البشر بدرجة نسبية ممتازة ويمكنهم التمييز بين صوتين إذا اختلفت تردداتهم بنسبة 0.3٪ أو أكثر. على سبيل المثال، تختلف 500.0 و 501.5 هرتز بشكل ملحوظ. النوتات الموسيقية هي أصوات ذات تردد معين يمكن أن تنتجها معظم الآلات الموسيقية وفي الموسيقى الغربية لها أسماء معينة، مثل A-sharp أو C أو E-flat.

يُطلق على مفهوم الشدة اسم الصوت. عند تردد معين، من الممكن تمييز اختلافات تبلغ حوالي 1 ديسيبل، ويمكن ملاحظة التغيير البالغ 3 ديسيبل بسهولة. لكن ارتفاع الصوت لا يرتبط بالكثافة وحدها. للتردد تأثير كبير على مدى ارتفاع الصوت. تبدو الأصوات القريبة من الترددات العالية والمنخفضة في نطاق السمع أقل صوتًا، لأن الأذن أقل حساسية عند تلك الترددات. عندما يعزف الكمان في منتصف C، فلا شك في أنه بيانو يعزف نفس النوتة. والسبب هو أن كل أداة تنتج مجموعة مميزة من الترددات والكثافات. نسمي تصورنا لهذه المجموعات من الترددات والكثافات جودة النغمة أو، بشكل أكثر شيوعًا، جرس الصوت. الجرس هو شكل الموجة التي تنشأ من العديد من الانعكاسات والرنين والتراكب في الآلة.

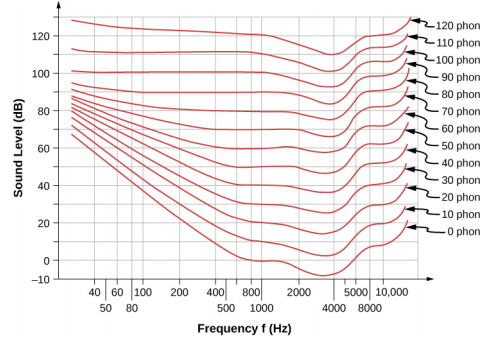
يتم استخدام وحدة تسمى الهاتف للتعبير عن الصوت العالي عدديًا. تختلف الهواتف عن وحدات الديسيبل لأن الهاتف عبارة عن وحدة إدراك جهارة الصوت، في حين أن الديسيبل هي وحدة الكثافة البدنية. $\PageIndex{4}$يوضح الشكل علاقة ارتفاع الصوت بالشدة (أو مستوى الشدة) والتردد للأشخاص ذوي السمع الطبيعي. الخطوط المنحنية هي منحنيات متساوية الصوت. يتم تمييز كل منحنى بصوت عالٍ في الهاتف. أي صوت على طول منحنى معين ينظر إليه الشخص العادي على أنه مرتفع بنفس القدر. تم تحديد المنحنيات من خلال قيام أعداد كبيرة من الأشخاص بمقارنة ارتفاع الأصوات بترددات مختلفة ومستويات شدة الصوت. عند تردد 1000 هرتز، تعتبر الهواتف مساوية عدديًا للديسيبل.

الرسم البياني هو مخطط مستوى الصوت بالديسيبل مقابل التردد في Herz. يتم رسم البيانات الخاصة بـ 0 و 10 و 20 و 30 و 40 و 50 و 60 و 70 و 80 و 90 و 100 و 110 و 120 هاتفًا. يتم رسم البيانات كخطوط منحنية مكدسة واحدة فوق الأخرى. — الشكل$\PageIndex{4}$: علاقة ارتفاع الصوت في الهاتف بمستوى الشدة (بالديسيبل) والشدة (بالوات لكل متر مربع) للأشخاص ذوي السمع العادي. الخطوط المنحنية عبارة عن منحنيات متساوية الصوت - يُنظر إلى جميع الأصوات على منحنى معين على أنها عالية بنفس القدر. يتم تعريف الهواتف والديسيبل لتكون هي نفسها عند 1000 هرتز.

مثال$\PageIndex{2}$: Measuring Loudness

ما مقدار ارتفاع الصوت في الهاتف لصوت ١٠٠ هرتز ومستوى شدته ٨٠ ديسيبل؟
ما مستوى شدة الصوت بالديسيبل لصوت بسرعة ٤٠٠٠٠ هرتز بصوت مرتفع ٧٠ فونًا؟
عند أي مستوى شدة سيكون لصوت ٨٠٠٠ هرتز نفس مستوى الصوت الذي يبلغ ٢٠٠ هرتز عند ٦٠ ديسيبل؟

إستراتيجية

$\PageIndex{4}$يجب الرجوع إلى الرسم البياني في الشكل لحل هذا المثال. للعثور على ارتفاع صوت معين، يجب معرفة مستوى تردده وشدته، وتحديد موقع تلك النقطة على الشبكة المربعة، ثم الاستكمال بين منحنيات الصوت للحصول على ارتفاع الصوت في الهاتف. بمجرد تحديد هذه النقطة، يمكن تحديد مستوى الكثافة من المحور الرأسي.

الحل

تحديد المعارف المعروفة: الشبكة المربعة للرسم البياني المتعلقة بالهواتف ووحدات الديسيبل عبارة عن مخطط لمستوى الكثافة مقابل التردد - كميتان فيزيائيتان: 100 هرتز عند 80 ديسيبل تقع في منتصف المسافة بين المنحنيات المحددة بـ 70 و80 فونًا. ابحث عن ارتفاع الصوت: 75 هاتف.
تحديد القيم المعروفة: تُعطى القيم لتكون 4000 هرتز عند 70 هاتفًا. اتبع منحنى 70-فون حتى يصل إلى 4000 هرتز. عند هذه النقطة، يكون أقل من خط 70 ديسيبل عند حوالي 67 ديسيبل. أوجد مستوى الكثافة: ٦٧ ديسيبل.
حدد موقع النقطة لصوت 200 هرتز و 60 ديسيبل. أوجد ارتفاع الصوت: تقع هذه النقطة أعلى بقليل من منحنى ٥٠ فونًا، وبالتالي فإن ارتفاع الصوت فيها هو ٥١ فونًا. ابحث عن مستوى هاتف 51 عند 8000 هرتز: 63 ديسيبل.

الأهمية

تحتوي هذه الإجابات، مثل جميع المعلومات المستخرجة من الشكل$\PageIndex{4}$، على شكوك تتعلق بعدة هواتف أو عدة وحدات ديسيبل، ويرجع ذلك جزئيًا إلى صعوبات في الاستكمال، ولكنه يتعلق في الغالب بعدم اليقين في منحنيات الصوت المتساوي.

التمارين$\PageIndex{2}$

وصف كيفية ارتباط السعة بصوت الصوت.

في هذا القسم، ناقشنا خصائص الصوت وكيف نسمع، ولكن كيف يتم إنتاج الأصوات التي نسمعها؟ مصادر الصوت المثيرة للاهتمام هي الآلات الموسيقية والصوت البشري، وسوف نناقش هذه المصادر. ولكن قبل أن نفهم كيف تنتج الآلات الموسيقية الصوت، نحتاج إلى النظر إلى الآليات الأساسية وراء هذه الآلات. تتضمن النظريات الكامنة وراء الآليات التي تستخدمها الآلات الموسيقية التداخل والتراكب والموجات الدائمة، والتي نناقشها في القسم التالي.

مثال\(\PageIndex{1A}\): Calculating Sound Intensity Levels

الحل

مثال\(\PageIndex{1B}\): Changing Intensity Levels of a Sound

الحل

التمارين\(\PageIndex{1}\)

مثال\(\PageIndex{2}\): Measuring Loudness

الحل

التمارين\(\PageIndex{2}\)