17.3: سرعة الصوت

Last updated
Save as PDF

Page ID: 199815

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

شرح العلاقة بين الطول الموجي وتردد الصوت
حدد سرعة الصوت في الوسائط المختلفة
اشتقاق معادلة سرعة الصوت في الهواء
حدد سرعة الصوت في الهواء لدرجة حرارة معينة

الصوت، مثل كل الموجات، ينتقل بسرعة معينة وله خصائص التردد والطول الموجي. يمكنك مشاهدة دليل مباشر على سرعة الصوت أثناء مشاهدة عرض الألعاب النارية (الشكل$\PageIndex{1}$). ترى وميض الانفجار قبل وقت طويل من سماع صوته وربما تشعر بموجة الضغط، مما يعني أن الصوت ينتقل بسرعة محدودة وأنه أبطأ بكثير من الضوء.

تظهر الصورة صورة للألعاب النارية الملونة التي تضيء سماء الليل. — الشكل$\PageIndex{1}$: عندما تنفجر قذيفة الألعاب النارية، فإننا ندرك الطاقة الضوئية قبل الطاقة الصوتية لأن الصوت ينتقل ببطء أكثر من الضوء.

يمكن أيضًا ملاحظة الفرق بين سرعة الضوء وسرعة الصوت أثناء العاصفة الكهربائية. غالبًا ما يُرى وميض الإضاءة قبل تصفيق الرعد. ربما سمعت أنه إذا قمت بحساب عدد الثواني بين الفلاش والصوت، يمكنك تقدير المسافة إلى المصدر. كل خمس ثوان تتحول إلى حوالي ميل واحد. ترتبط سرعة أي موجة بترددها وطولها الموجي

\[v = f \lambda, \label{17.3}\]

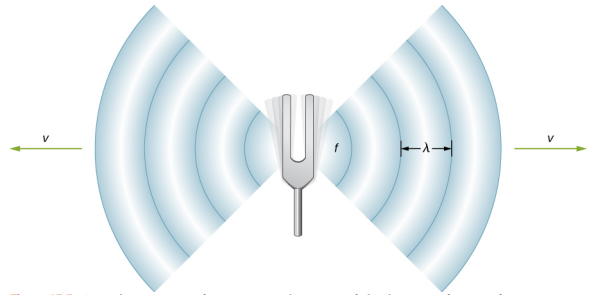
أين$v$ سرعة الموجة،$f$ هو ترددها،$\lambda$ وطولها الموجي. تذكر من Waves أن الطول الموجي هو طول الموجة كما تم قياسه بين نقاط متطابقة متسلسلة. على سبيل المثال، بالنسبة لموجة المياه السطحية أو الموجة الجيبية على سلسلة، يمكن قياس الطول الموجي بين أي نقطتين متتابعتين ملائمتين بنفس الارتفاع والانحدار، مثل بين قمتين متتابعتين أو حوضين متتابعين. وبالمثل، فإن الطول الموجي للموجة الصوتية هو المسافة بين الأجزاء المتطابقة المتسلسلة من الموجة - على سبيل المثال، بين الضغطات المتسلسلة (الشكل$\PageIndex{2}$). التردد هو نفس تردد المصدر وهو عدد الموجات التي تمر بنقطة لكل وحدة زمنية.

الصورة عبارة عن رسم تخطيطي لشوكة رنانة تنبعث منها موجات صوتية. — الشكل$\PageIndex{2}$: تنبعث موجة صوتية من مصدر، مثل شوكة رنانة، تهتز بتردد f، وتنتشر بسرعة v ولها طول موجي$\lambda$.

سرعة الصوت في الوسائط المختلفة

$\PageIndex{1}$يوضح الجدول أن سرعة الصوت تختلف اختلافًا كبيرًا في الوسائط المختلفة. تعتمد سرعة الصوت في الوسط على مدى سرعة نقل الطاقة الاهتزازية عبر الوسيط. لهذا السبب، يعتمد اشتقاق سرعة الصوت في الوسط على الوسيط وعلى حالة الوسيط. بشكل عام، تعتمد معادلة سرعة الموجة الميكانيكية في الوسط على الجذر التربيعي لقوة الاستعادة، أو الخاصية المرنة، مقسومًا على خاصية القصور الذاتي،

\[v = \sqrt{\frac{\text{elastic property}}{\text{inertial property}}} \ldotp\]

أيضًا، تلبي الموجات الصوتية معادلة الموجة المشتقة في Waves،

\[\frac{\partial^{2} y (x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y (x,t)}{\partial t^{2}} \ldotp\]

تذكر من Waves أن سرعة الموجة على الخيط تساوي$v = \sqrt{\frac{F_{T}}{\mu}}$، حيث تكون قوة الاستعادة هي الشد في السلسلة F _T والكثافة الخطية$\mu$ هي خاصية القصور الذاتي. في السائل، تعتمد سرعة الصوت على معامل الكتلة والكثافة،

\[v = \sqrt{\frac{B}{\rho}} \ldotp \label{17.4}\]

تعتمد سرعة الصوت في مادة صلبة على معامل يونغ للوسط والكثافة،

\[v = \sqrt{\frac{Y}{\rho}} \ldotp \label{17.5}\]

في الغاز المثالي (راجع النظرية الحركية للغازات)، تكون معادلة سرعة الصوت

\[v = \sqrt{\frac{\gamma RT_{K}}{M}}, \label{17.6}\]

أين$\gamma$ هو المؤشر الحراري، R = 8.31 J/mol • K هو ثابت الغاز، T _K هي درجة الحرارة المطلقة في الكيلفين، و M هي الكتلة الجزيئية. بشكل عام، كلما كانت الوسيلة أكثر صلابة (أو أقل انضغاطًا)، زادت سرعة الصوت. هذه الملاحظة مماثلة لحقيقة أن تردد الحركة التوافقية البسيطة يتناسب طرديًا مع صلابة الجسم المتذبذب كما تم قياسه بـ k، ثابت الزنبرك. كلما زادت كثافة الوسيط، كانت سرعة الصوت أبطأ. هذه الملاحظة مماثلة لحقيقة أن تردد الحركة التوافقية البسيطة يتناسب عكسياً مع m، كتلة الجسم المتذبذب. سرعة الصوت في الهواء منخفضة، لأن الهواء قابل للضغط بسهولة. نظرًا لأن السوائل والمواد الصلبة صلبة نسبيًا ويصعب ضغطها، فإن سرعة الصوت في هذه الوسائط تكون عمومًا أكبر من سرعة الغازات.

الجدول$\PageIndex{1}$: سرعة الصوت في الوسائط المختلفة
متوسط	فولت (متر/ثانية)
الغازات عند 0 درجة مئوية
الهواء	331
ثنائي أكسيد الكربون	259
أكسجين	316
هيليوم	965
هيدروجين	1290
السوائل عند 20 درجة مئوية
إيثانول	1160
زئبق	1450
ماء، طازج	1480
مياه البحر	1540
الأنسجة البشرية	1540
المواد الصلبة (الطولية أو السائبة)
مطاط مبركن	54
بولي إيثيلين	920
ماربل	3810
زجاج، بيركس	5640
الرصاص	1960
ألمنيوم	5120
ستيل	5960

نظرًا لأن سرعة الصوت تعتمد على كثافة المادة، وتعتمد الكثافة على درجة الحرارة، فهناك علاقة بين درجة الحرارة في وسط معين وسرعة الصوت في الوسط. بالنسبة للهواء عند مستوى سطح البحر، يتم تحديد سرعة الصوت من خلال

\[v = 331\; m/s \sqrt{1 + \frac{T_{C}}{273 °C}} = 331\; m/s \sqrt{\frac{T_{K}}{273\; K}} \label{17.7}\]

حيث تكون درجة الحرارة في المعادلة الأولى (المشار إليها بـ T _C) بالدرجات المئوية ودرجة الحرارة في المعادلة الثانية (المشار إليها بـ T _K) تكون بالكلفن. ترتبط سرعة الصوت في الغازات بمتوسط سرعة الجسيمات في الغاز،

\[v_{rms} = \sqrt{\frac{3k_{B}T}{m}}.\]

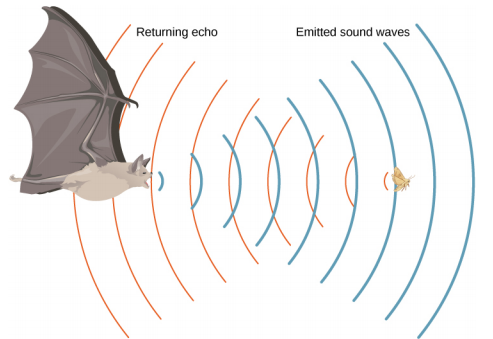
$k_B$أين ثابت بولتزمان (1.38 × 10 ⁻²³ J/K) وm هو كتلة كل جسيم (متطابق) في الغاز. لاحظ أن v تشير إلى سرعة الانتشار المتماسك للاضطراب (الموجة)، بينما$v_{rms}$ تصف سرعات الجسيمات في الاتجاهات العشوائية. وبالتالي، فمن المعقول أن تعتمد سرعة الصوت في الهواء والغازات الأخرى على الجذر التربيعي لدرجة الحرارة. على الرغم من أن هذا لا يستهان به، إلا أنه ليس اعتمادًا قويًا. عند 0 درجة مئوية، تبلغ سرعة الصوت 331 م/ث، بينما عند 20.0 درجة مئوية، تكون سرعة الصوت 343 متر/ثانية، أي أقل من زيادة بنسبة 4٪. $\PageIndex{3}$يوضح الشكل كيفية استخدام الخفاش لسرعة الصوت لاستشعار المسافات.

الصورة عبارة عن رسم لمضرب طائر يصدر موجات صوتية. تنعكس الأمواج من الحشرة الطائرة وتعود إلى الخفافيش. — الشكل$\PageIndex{1}$: يستخدم الخفاش أصداء الصوت ليجد طريقه للقبض على الفريسة. يتناسب وقت عودة الصدى بشكل مباشر مع المسافة.

اشتقاق سرعة الصوت في الهواء

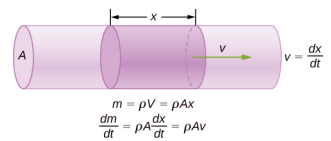
كما ذكرنا سابقًا، تعتمد سرعة الصوت في الوسيط على الوسيط وحالة الوسيط. يبدأ اشتقاق معادلة سرعة الصوت في الهواء بمعدل تدفق الكتلة ومعادلة الاستمرارية التي تمت مناقشتها في ميكانيكا الموائع. ضع في اعتبارك تدفق السوائل عبر أنبوب بمساحة مقطعية$A$ (الشكل$\PageIndex{4}$). الكتلة في حجم صغير$x$ من طول الأنبوب تساوي الكثافة مضروبة في الحجم، أو

\[m = \rho V = \rho Ax.\]

معدل تدفق الكتلة هو

\[\frac{dm}{dt} = \frac{d}{dt} (\rho V) = \frac{d}{dt} (\rho Ax) = \rho A \frac{dx}{dt} = \rho Av \ldotp\]

تنص معادلة الاستمرارية من ميكانيكا الموائع على أن معدل تدفق الكتلة إلى الحجم يجب أن يساوي معدل تدفق الكتلة خارج الحجم،

\[\rho_{in} A_{in}v_{in} = \rho_{out} A_{out}v_{out}.\]

الصورة عبارة عن رسم تخطيطي لكتلة تتدفق من خلالها السرعة v للمسافة x عبر الأسطوانة مع منطقة المقطع العرضي A. — الشكل:$\PageIndex{1}$ كتلة السائل في الحجم تساوي الكثافة في الحجم،.$m = \rho V = \rho Ax$ معدل تدفق الكتلة هو المشتق الزمني للكتلة.

الآن فكر في موجة صوتية تتحرك عبر طرد من الهواء. قطعة الهواء عبارة عن حجم صغير من الهواء بحدود خيالية (الشكل$\PageIndex{5}$). تُعطى الكثافة ودرجة الحرارة والسرعة على أحد جانبي حجم السائل على النحو التالي: T$\rho$، v، وعلى الجانب الآخر هي$\rho$ + d$\rho$،$T + dT$،$v + dv$.

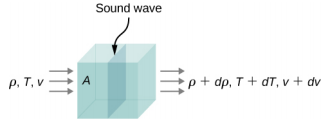
الصورة عبارة عن رسم تخطيطي لموجة صوتية تتحرك عبر حجم السائل. تتغير كثافة ودرجة حرارة وسرعة السائل من جانب إلى آخر. — الشكل$\PageIndex{1}$: تتحرك موجة صوتية عبر حجم السائل. تتغير كثافة ودرجة حرارة وسرعة السائل من جانب إلى آخر.

تنص معادلة الاستمرارية على أن معدل تدفق الكتلة الذي يدخل الحجم يساوي معدل تدفق الكتلة الذي يغادر الحجم، لذلك

\[\rho Av = (\rho + d \rho)A(v + dv) \ldotp\]

يمكن تبسيط هذه المعادلة، مع ملاحظة أن المنطقة تلغي مع الأخذ في الاعتبار أن ضرب اثنين من القيم المتناهية الصغر يساوي تقريبًا الصفر: d$\rho$ (dv) ≈ 0،

\[\begin{split} \rho v & = (\rho + d \rho)(v + dv) \\ & = \rho v + \rho (dv) + (d \rho)v + (d \rho)(dv) \\ 0 & = \rho (dv) + (d \rho) v \\ \rho\; dv & = -v\; d \rho \ldotp \end{split}\]

القوة الصافية على حجم السائل (الشكل$\PageIndex{6}$) تساوي مجموع القوى على الوجه الأيسر والوجه الأيمن:

\[\begin{split} F_{net} & = p\; dy\; dz - (p + dp)\; dy\; dz \ & = p\; dy\; dz\; - p\; dy\; dz - dp\; dy\; dz \\ & = -dp\; dy\; dz \\ ma & = -dp\; dy\; dz \ldotp \end{split}\]

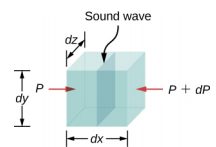
الصورة عبارة عن رسم تخطيطي لموجة صوتية تتحرك عبر حجم السائل مع جوانب الأبعاد dx و dy و dz. يختلف الضغط على الجانبين المعاكسين. — الشكل$\PageIndex{1}$: تتحرك موجة صوتية عبر حجم السائل. يمكن العثور على القوة على كل وجه من خلال الضغط على المنطقة.

الشكل$\PageIndex{6}$:

التسارع هو القوة المقسمة على الكتلة والكتلة تساوي الكثافة مضروبة في الحجم، m =$\rho$ V =$\rho$ dx dy dz. لدينا

\[\begin{split} ma & = -dp\; dy\; dz \\ a & = - \frac{dp\; dy\; dz}{m} = - \frac{dp\; dy\; dz}{\rho\; dx\; dy\; dz} = - \frac{dp}{\rho\; dx} \\ \frac{dv}{dt} & = - \frac{dp}{\rho\; dx} \\ dv & = - \frac{dp}{\rho dx} dt = - \frac{dp}{\rho} \frac{1}{v} \\ \rho v\; dv & = -dp \ldotp \end{split}\]

من معادلة الاستمرارية$\rho$ dv = −vd$\rho$، نحصل على

\[\begin{split} \rho v\; dv & = -dp \\ (-v\; d \rho)v & = -dp \\ v & = \sqrt{\frac{dp}{d \rho}} \ldotp \end{split}\]

ضع في اعتبارك موجة صوتية تتحرك عبر الهواء. أثناء عملية ضغط الغاز وتوسيعه، لا تتم إضافة حرارة أو إزالتها من النظام. تُعرف العملية التي لا تتم فيها إضافة الحرارة أو إزالتها من النظام بنظام ثابت الحرارة. تمت تغطية العمليات الأديباتية بالتفصيل في القانون الأول للديناميكا الحرارية، ولكن في الوقت الحالي يكفي القول أنه بالنسبة للعملية الأديباتية$pV^{\gamma} = \text{constant}$، أين$p$ الضغط،$V$ هو الحجم، وغاما ($\gamma$) هو ثابت يعتمد على الغاز. للهواء،$\gamma$ = 1.40. تساوي الكثافة عدد المولات مضروبًا في الكتلة المولية مقسومًا على الحجم، وبالتالي فإن الحجم يساوي V =$\frac{nM}{\rho}$. عدد الشامات والكتلة المولية ثابت ويمكن امتصاصه في الثابت p$\left(\dfrac{1}{\rho}\right)^{\gamma}$ = الثابت. يؤدي أخذ اللوغاريتم الطبيعي لكلا الجانبين إلى p −$\gamma$ ln$\rho$ = ثابت. وبالتفريق فيما يتعلق بالكثافة، تصبح المعادلة

\[\begin{split} \ln p - \gamma \ln \rho & = constant \\ \frac{d}{d \rho} (\ln p - \gamma \ln \rho) & = \frac{d}{d \rho} (constant) \\ \frac{1}{p} \frac{dp}{d \rho} - \frac{\gamma}{\rho} & = 0 \\ \frac{dp}{d \rho} & = \frac{\gamma p}{\rho} \ldotp \end{split}\]

إذا كان من الممكن اعتبار الهواء غازًا مثاليًا، فيمكننا استخدام قانون الغاز المثالي:

\[\begin{split} pV & = nRT = \frac{m}{M} RT \\ p & = \frac{m}{V} \frac{RT}{M} = \rho \frac{RT}{M} \ldotp \end{split}\]

هنا M هي الكتلة المولية للهواء:

\[\frac{dp}{d \rho} = \frac{\gamma p}{\rho} = \frac{\gamma \left(\rho \frac{RT}{M}\right)}{\rho} = \frac{\gamma RT}{M} \ldotp\]

نظرًا لأن سرعة الصوت تساوي v =$\sqrt{\frac{dp}{d \rho}}$، فإن السرعة تساوي

\[v = \sqrt{\frac{\gamma RT}{M}} \ldotp\]

لاحظ أن السرعة تكون أسرع في درجات الحرارة المرتفعة وأبطأ للغازات الثقيلة. بالنسبة للهواء،$\gamma$ = 1.4، M = 0.02897 كجم/مول، R = 8.31 J/mol • K. إذا كانت درجة الحرارة T _C = 20 درجة مئوية (T = 293 K)، فإن سرعة الصوت هي v = 343 m/s،$\sqrt{\frac{\gamma RT}{M}}$ ويمكن تبسيط معادلة سرعة الصوت في الهواء = لإعطاء معادلة سرعة الصوت في الهواء كدالة لـ درجة الحرارة المطلقة:

\[\begin{split} v & = \sqrt{\frac{\gamma RT}{M}} \\ & = \sqrt{\frac{\gamma RT}{M} \left(\dfrac{273\; K}{273\; K}\right)} = \sqrt{\frac{(273\; K) \gamma R}{M}} \sqrt{\frac{T}{273\; K}} \\ & \approx 331\; m/s \sqrt{\frac{T}{273\; K}} \ldotp \end{split}\]

واحدة من أهم خصائص الصوت هي أن سرعته مستقلة تقريبًا عن التردد. هذه الاستقلالية صحيحة بالتأكيد في الهواء الطلق للأصوات في النطاق المسموع. إذا لم يكن هذا الاستقلال صحيحًا، فستلاحظه بالتأكيد للموسيقى التي تعزفها فرقة موسيقية في ملعب كرة قدم، على سبيل المثال. لنفترض أن الأصوات عالية التردد انتقلت بشكل أسرع - فكلما ابتعدت عن الفرقة، زاد تأخر الصوت الصادر عن الآلات ذات النغمة المنخفضة عن الصوت العالي. لكن الموسيقى من جميع الآلات تصل بإيقاع مستقل عن المسافة، لذلك يجب أن تنتقل جميع الترددات بنفس السرعة تقريبًا. أذكر ذلك

\[v = f \lambda \ldotp\]

في وسط معين في ظل ظروف ثابتة،$v$ يكون ثابتًا، لذلك هناك علاقة بين$f$ و$\lambda$؛ كلما زاد التردد، قل طول الموجة (الشكل$\PageIndex{7}$).

الصورة عبارة عن رسم تخطيطي لنظام مكبر صوت يصدر موجات صوتية. تنبعث أصوات التردد المنخفض من السماعة الكبيرة السفلية؛ وتنبعث الأصوات ذات التردد العالي من السماعة الصغيرة العلوية. — الشكل$\PageIndex{7}$: نظرًا لأنها تنتقل بنفس السرعة في وسط معين، يجب أن يكون للأصوات ذات التردد المنخفض طول موجة أكبر من الأصوات عالية التردد. هنا، تنبعث الأصوات ذات التردد المنخفض من السماعة الكبيرة، والتي تسمى مكبر الصوت، بينما تنبعث الأصوات ذات التردد العالي من السماعة الصغيرة، والتي تسمى مكبر الصوت.

مثال$\PageIndex{1}$: Calculating Wavelengths

احسب الأطوال الموجية للأصوات عند أقصى حدود النطاق المسموع، 20 و20000 هرتز، في هواء 30.0 درجة مئوية. (افترض أن قيم التردد دقيقة لشخصيتين مهمتين.)

إستراتيجية

للعثور على الطول الموجي من التردد، يمكننا استخدامه$v = f \lambda$.

الحل

تحديد الأشياء المعروفة. $v$يتم إعطاء القيمة لـ\[v = 331\; m/s \sqrt{\frac{T}{273\; K}} \ldotp \nonumber\]
قم بتحويل درجة الحرارة إلى كلفن ثم أدخل درجة الحرارة في المعادلة\[v = 331\; m/s \sqrt{\frac{303\; K}{273\; K}} = 348.7\; m/s \ldotp \nonumber\]
حل العلاقة بين السرعة والطول الموجي لـ$\lambda$: $$\ lambda =\ frac {v} {f}\ ldotp\ nonumber$$
أدخل السرعة والحد الأدنى للتردد لإعطاء الطول الموجي الأقصى:\[\lambda_{max} = \frac{348.7\; m/s}{20\; Hz} = 17\; m \ldotp \nonumber\]
أدخل السرعة والحد الأقصى للتردد لإعطاء الحد الأدنى للطول الموجي:\[\lambda_{min} = \frac{348.7\; m/s}{20,000\; Hz} = 0.017\; m = 1.7\; cm \ldotp \nonumber\]

الدلالة

نظرًا لأن$f$ حاصل الضرب في$\lambda$ يساوي ثابتًا، فالأصغر$f$ هو،$\lambda$ يجب أن يكون الأكبر، والعكس صحيح.

يمكن أن تتغير سرعة الصوت عندما ينتقل الصوت من وسيط إلى آخر، ولكن عادة ما يظل التردد كما هو. هذا مشابه لتردد الموجة على سلسلة تساوي تردد القوة التي تتأرجح في السلسلة. إذا$v$ تغيرت$f$ وظلت كما هي،$\lambda$ فيجب تغيير الطول الموجي. وذلك لأنه$v = f \lambda$ كلما زادت سرعة الصوت، زاد طول طوله الموجي لتردد معين.

التمارين$\PageIndex{1}$

تخيل أنك تلاحظ انفجار قذيفتين من الألعاب النارية. تسمع انفجار واحدة بمجرد رؤيتها. ومع ذلك، ترى الغلاف الآخر لعدة أجزاء من الثانية قبل سماع الانفجار. اشرح سبب ذلك.

على الرغم من أن الموجات الصوتية في السائل طولية، إلا أن الموجات الصوتية في المواد الصلبة تنتقل كموجات طولية وموجات عرضية. تعد الموجات الزلزالية، التي هي في الأساس موجات صوتية في القشرة الأرضية تنتجها الزلازل، مثالًا مثيرًا للاهتمام لكيفية اعتماد سرعة الصوت على صلابة الوسط. تنتج الزلازل موجات طولية وعرضية، وتنتقل هذه الموجات بسرعات مختلفة. معامل الكتلة للجرانيت أكبر من معامل القص. ولهذا السبب، فإن سرعة الموجات الطولية أو موجات الضغط (الموجات P) في الزلازل في الجرانيت أعلى بكثير من سرعة الموجات العرضية أو موجات القص (الموجات S). ينتقل كلا النوعين من موجات الزلازل بشكل أبطأ في المواد الأقل صلابة، مثل الرواسب. تتراوح سرعات الموجات P من 4 إلى 7 كم/ثانية، وتتراوح سرعة الموجات S من 2 إلى 5 كم/ثانية، وكلاهما أسرع في المواد الأكثر صلابة. تتقدم الموجة P بشكل تدريجي على الموجة S أثناء انتقالها عبر القشرة الأرضية. يتم استخدام الوقت بين الموجات P- و S بشكل روتيني لتحديد المسافة إلى مصدرها، مركز الزلزال. نظرًا لأن موجات S لا تمر عبر النواة السائلة، يتم إنتاج منطقتين للظل (الشكل$\PageIndex{8}$).

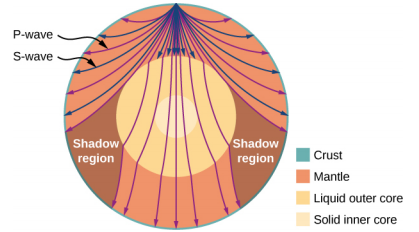
الصورة عبارة عن رسم لموجات P و S التي تنتقل من مصدر. يشار أيضًا إلى مناطق الظل، حيث تكون موجات S غائبة. هناك ملصقات مشفرة بالألوان للقشرة والعباءة والنواة الخارجية السائلة والنواة الداخلية الصلبة. — الشكل$\PageIndex{8}$: تنتج الزلازل موجات طولية (موجات P) وموجات عرضية (موجات S)، وتنتقل بسرعات مختلفة. تنتقل كلتا الموجتين بسرعات مختلفة في مناطق مختلفة من الأرض، ولكن بشكل عام، تنتقل الموجات P بشكل أسرع من موجات S. لا يمكن دعم موجات S بواسطة النواة السائلة، مما ينتج مناطق الظل.

عندما تتحرك الموجات الصوتية بعيدًا عن مكبر الصوت، أو بعيدًا عن مركز الزلزال، تنخفض طاقتها لكل وحدة مساحة. هذا هو السبب في أن الصوت مرتفع جدًا بالقرب من مكبر الصوت ويصبح أقل صوتًا عندما تبتعد عن السماعة. وهذا يفسر أيضًا سبب حدوث قدر كبير من الضرر في مركز الزلزال ولكن يتم الشعور بالهزات فقط في المناطق البعيدة عن مركز الزلزال. تُعرف الطاقة لكل وحدة مساحة بالكثافة، وفي القسم التالي، سنناقش كيف تعتمد الكثافة على المسافة من المصدر.

مثال\(\PageIndex{1}\): Calculating Wavelengths

الحل

التمارين\(\PageIndex{1}\)