17.2: الموجات الصوتية
- Page ID
- 199835
- شرح الفرق بين الصوت والسمع
- وصف الصوت كموجة
- ضع قائمة بالمعادلات المستخدمة لنمذجة الموجات الصوتية
- وصف الضغط والانحرافات من حيث صلتها بالصوت
الظاهرة الفيزيائية للصوت هي اضطراب المادة التي تنتقل من مصدرها إلى الخارج. السمع هو إدراك الصوت، تمامًا كما أن الرؤية هي إدراك الضوء المرئي. على المستوى الذري، الصوت هو اضطراب في الذرات أكثر ترتيبًا بكثير من حركاتها الحرارية. في كثير من الحالات، يكون الصوت موجة دورية، وتخضع الذرات لحركة توافقية بسيطة. وبالتالي، يمكن للموجات الصوتية أن تحفز التذبذبات وتأثيرات الرنين (الشكل\(\PageIndex{2}\)).
يُظهر هذا الفيديو موجات على سطح كأس نبيذ مدفوعة بموجات صوتية من مكبر صوت. مع اقتراب تردد الموجة الصوتية من تردد الرنين لزجاج النبيذ، تزداد سعة وتردد الموجات على كأس النبيذ. عندما يتم الوصول إلى تردد الرنين، يتحطم الزجاج.
فيديو\(\PageIndex{1}\): كسر كأس نبيذ باستخدام الرنين من خلال تشغيل الصوت بتردد الرنين. https://www.youtube.com/watch?v=17tqXgvCN0E
ينتج مكبر الصوت موجة صوتية عن طريق تذبذب المخروط، مما يتسبب في اهتزازات جزيئات الهواء. في الشكل\(\PageIndex{2}\)، يهتز مكبر صوت بتردد وسعة ثابتين، مما ينتج اهتزازات في جزيئات الهواء المحيطة. عندما تتأرجح السماعة ذهابًا وإيابًا، فإنها تنقل الطاقة إلى الهواء، في الغالب كطاقة حرارية. لكن جزءًا صغيرًا من طاقة مكبر الصوت يذهب إلى ضغط الهواء المحيط وتوسيعه، مما يخلق ضغوطًا محلية أعلى وأقل قليلاً. تتحرك هذه الضغطات (مناطق الضغط العالي) والفواصل النادرة (مناطق الضغط المنخفض) كموجات ضغط طولية لها نفس تردد مكبر الصوت - إنها الاضطراب الذي يمثل موجة صوتية. (تكون الموجات الصوتية في الهواء ومعظم السوائل طولية، لأن السوائل ليس لها قوة قص تقريبًا. في المواد الصلبة، يمكن أن تكون الموجات الصوتية عرضية وطولية.)
\(\PageIndex{2a}\)يوضِّح الشكل الانضغاطات والفواصل النادرة، كما يوضِّح رسمًا بيانيًا لقياس الضغط مقابل المسافة من السماعة. عندما يتحرك مكبر الصوت في الاتجاه السيني الموجب، فإنه يدفع جزيئات الهواء ويخرجها من مواضع الاتزان. عندما يتحرك مكبر الصوت في الاتجاه السالب x، تتحرك جزيئات الهواء مرة أخرى نحو مواضع الاتزان بسبب قوة الاستعادة. تتأرجح جزيئات الهواء بحركة توافقية بسيطة حول مواضع الاتزان الخاصة بها، كما هو موضح في الشكل\(\PageIndex{2b}\). لاحظ أن الموجات الصوتية في الهواء طولية، وفي الشكل، تنتشر الموجة في الاتجاه السيني الموجب وتتأرجح الجزيئات بالتوازي مع الاتجاه الذي تنتشر فيه الموجة.
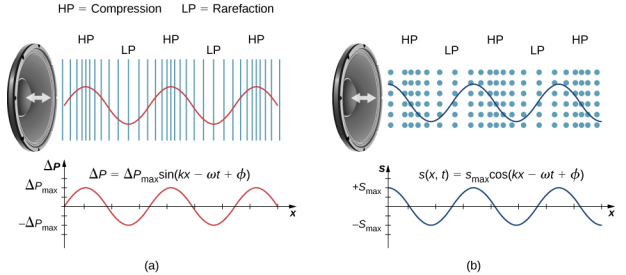
يمكن تصميم الصوت كموجة ضغط من خلال النظر في التغيير في الضغط من متوسط الضغط،
\[\Delta P = \Delta P_{max} \sin (kx \mp \omega t + \phi) \ldotp \label{17.1}\]
تشبه هذه المعادلة معادلات الموجة الدورية التي تظهر في Waves، حيث\(\Delta\) P هو التغيير في الضغط،\(\Delta P_{max}\) وهو الحد الأقصى للتغيير في الضغط،\(k = \frac{2 \pi}{\lambda}\) وهو رقم الموجة،\(\omega = \frac{2 \pi}{T} = 2 \pi f\) وهو التردد الزاوي،\(\phi\) وهو المرحلة الأولية. يمكن تحديد سرعة الموجة من
\[v = \frac{\omega}{k} = \frac{\lambda}{T}.\]
يمكن أيضًا تصميم الموجات الصوتية من حيث إزاحة جزيئات الهواء. يمكن نمذجة إزاحة جزيئات الهواء باستخدام دالة جيب التمام:
\[s(x, t) = s_{max} \cos(kx \mp \omega t + \phi) \ldotp \label{17.2}\]
في هذه المعادلة،\(s\) هي الإزاحة\(s_{max}\) وهي الحد الأقصى للإزاحة.
لا يظهر في الشكل سعة الموجة الصوتية لأنها تتناقص مع المسافة من مصدرها، لأن طاقة الموجة تنتشر على مساحة أكبر وأكبر. تنخفض الكثافة عندما تبتعد عن السماعة، كما تمت مناقشته في Waves. يتم امتصاص الطاقة أيضًا بواسطة الأجسام وتحويلها إلى طاقة حرارية من خلال لزوجة الهواء. بالإضافة إلى ذلك، أثناء كل ضغط، ينتقل القليل من الحرارة إلى الهواء؛ وخلال كل عملية تخفيف، تقل عمليات نقل الحرارة من الهواء، وتقلل عمليات نقل الحرارة هذه من الاضطراب المنظم إلى حركات حرارية عشوائية. يعتمد مدى أهمية انتقال الحرارة من الضغط إلى التخلخل على مدى تباعدهما - أي أنه يعتمد على الطول الموجي. يعد الطول الموجي والتردد والسعة وسرعة الانتشار من الخصائص المهمة للصوت، كما هو الحال بالنسبة لجميع الموجات.


