14.9: اللزوجة والاضطراب
- Page ID
- 200151
- اشرح ما هي اللزوجة
- احسب التدفق والمقاومة باستخدام قانون Poiseuille
- اشرح كيف ينخفض الضغط بسبب المقاومة
- احسب رقم رينولدز لجسم يتحرك عبر سائل
- استخدم رقم رينولدز للنظام لتحديد ما إذا كان رقائقيًا أم مضطربًا
- وصف الظروف التي بموجبها يكون للكائن سرعة طرفية
في تطبيقات قوانين نيوتن، التي قدمت مفهوم الاحتكاك، رأينا أن جسمًا ينزلق عبر الأرض بسرعة أولية ولا توجد قوة مطبقة يستقر بسبب قوة الاحتكاك. يعتمد الاحتكاك على أنواع المواد الملامسة ويتناسب مع القوة العادية. ناقشنا أيضًا مقاومة السحب والهواء في نفس الفصل. أوضحنا أنه عند السرعات المنخفضة، يتناسب السحب مع السرعة، بينما في السرعات العالية، يتناسب السحب مع مربع السرعة. في هذا القسم، نقدم قوى الاحتكاك التي تؤثر على السوائل أثناء الحركة. على سبيل المثال، يخضع السائل المتدفق عبر الأنبوب للمقاومة، وهو نوع من الاحتكاك، بين السائل والجدران. يحدث الاحتكاك أيضًا بين طبقات السوائل المختلفة. تؤثر هذه القوى المقاومة على طريقة تدفق السائل عبر الأنبوب.
اللزوجة والتدفق الصفحي
عندما تسكب لنفسك كوبًا من العصير، يتدفق السائل بحرية وبسرعة. ولكن إذا صببت شراب القيقب على الفطائر، فإن هذا السائل يتدفق ببطء ويلتصق بالإبريق. الفرق هو احتكاك السوائل، سواء داخل السائل نفسه أو بين السائل والمناطق المحيطة به. نسمي هذه الخاصية لزوجة السوائل. يحتوي العصير على لزوجة منخفضة، بينما يحتوي الشراب على لزوجة عالية.
يعتمد التعريف الدقيق لللزوجة على التدفق الصفحي أو غير المضطرب. \(\PageIndex{1}\)يوضح الشكل بشكل تخطيطي كيف يختلف التدفق الصفحي والمضطرب. عندما يكون التدفق رقائقيًا، تتدفق الطبقات دون خلط. عندما يكون التدفق مضطربًا، تختلط الطبقات، وتحدث سرعات كبيرة في اتجاهات أخرى غير الاتجاه العام للتدفق.
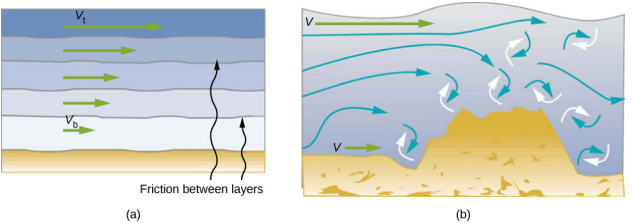
الاضطراب هو تدفق مائع تختلط فيه الطبقات معًا عبر الدوامات والدوامات. لها سببان رئيسيان. أولاً، يؤدي أي عائق أو زاوية حادة، كما هو الحال في الصنبور، إلى حدوث اضطراب من خلال إضفاء سرعات عمودية على التدفق. ثانيًا، تسبب السرعات العالية اضطرابًا. يمكن أن يشكل السحب بين طبقات السائل المتجاورة وبين السائل والمناطق المحيطة به دوامات ودوامات إذا كانت السرعة كبيرة بما يكفي. في الشكل\(\PageIndex{2}\)، تصل سرعة الدخان المتسارع إلى النقطة التي يبدأ فيها الدوران بسبب السحب بين الدخان والهواء المحيط.

\(\PageIndex{3}\)يوضح الشكل كيفية قياس اللزوجة للسائل. يتم وضع السائل المراد قياسه بين لوحين متوازيين. يتم تثبيت اللوحة السفلية بشكل ثابت، بينما يتم تحريك اللوحة العلوية إلى اليمين وسحب السائل معها. لا تتحرك طبقة (أو صفيحة) السائل الملامس لأي من اللوحين بالنسبة للوحة، لذلك تتحرك الطبقة العليا بسرعة v بينما تظل الطبقة السفلية في حالة سكون. كل طبقة متتالية من الأعلى إلى الأسفل تمارس قوة على الطبقة الموجودة أسفلها، في محاولة لسحبها، مما ينتج عنه تباين مستمر في السرعة من v إلى 0 كما هو موضح. يتم الحرص على ضمان أن يكون التدفق رقائقيًا، أي أن الطبقات لا تختلط. الحركة في الشكل تشبه حركة القص المستمرة. تتمتع السوائل بمقاومة قص صفرية، ولكن معدل قصها يرتبط بنفس العوامل الهندسية A و L مثل تشوه القص للمواد الصلبة. في الرسم التخطيطي، يكون السائل في حالة سكون في البداية. يتم تسريع طبقة السائل الملامسة للوحة المتحركة وتبدأ في التحرك بسبب الاحتكاك الداخلي بين اللوحة المتحركة والسائل. الطبقة التالية تتلامس مع الطبقة المتحركة؛ نظرًا لوجود احتكاك داخلي بين الطبقتين، فإنه يتسارع أيضًا، وهكذا عبر عمق السائل. يوجد أيضًا احتكاك داخلي بين اللوحة الثابتة والطبقة السفلية من السائل بجوار لوحة المحطة. القوة مطلوبة للحفاظ على حركة اللوحة بسرعة ثابتة بسبب الاحتكاك الداخلي.
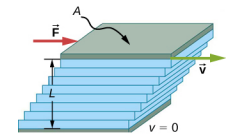
القوة F مطلوبة للحفاظ على\(\PageIndex{3}\) تحرك اللوحة العلوية في الشكل بسرعة ثابتة v، وقد أظهرت التجارب أن هذه القوة تعتمد على أربعة عوامل. أولاً، تتناسب F بشكل مباشر مع v (حتى تكون السرعة عالية جدًا بحيث يحدث الاضطراب - ثم تكون هناك حاجة إلى قوة أكبر بكثير، ولديها اعتماد أكثر تعقيدًا على v). ثانيًا، تتناسب F مع المنطقة A من اللوحة. تبدو هذه العلاقة معقولة، حيث أن A تتناسب طرديًا مع كمية السائل الذي يتم نقله. ثالثًا، يتناسب F عكسيًا مع المسافة بين اللوحين L. هذه العلاقة معقولة أيضًا؛ L يشبه ذراع الرافعة، وكلما زاد ذراع الرافعة، قلت القوة المطلوبة. رابعًا، تتناسب F بشكل مباشر مع معامل اللزوجة،\(\eta\) فكلما زادت اللزوجة، زادت القوة المطلوبة. يتم دمج هذه التبعيات في المعادلة
\[F = \eta \frac{vA}{L} \ldotp\]
تعطينا هذه المعادلة تعريفًا عمليًا لزوجة الموائع\(\eta\). حل\(\eta\) للعطاء
\[\eta = \frac{FL}{vA} \label{14.17}\]
الذي يحدد اللزوجة من حيث كيفية قياسها. وحدة اللزوجة SI هي\(\frac{N\; \cdotp m}{[(m/s)m^{2}]}\) = (N/m 2) s أو Pa • s.\(\PageIndex{1}\) يسرد الجدول معاملات اللزوجة للسوائل المختلفة. تختلف اللزوجة من سائل إلى آخر بعدة درجات من حيث الحجم. كما قد تتوقع، فإن لزوجة الغازات أقل بكثير من لزوجة السوائل، وغالبًا ما تعتمد هذه اللزوجة على درجة الحرارة.
| سائل | درجة الحرارة (درجة مئوية) | اللزوجة\(\eta \times 10^{3}\) |
|---|---|---|
| الهواء | 0 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >0.0171 |
| 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >0.0181 | |
| 40 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >0.0190 | |
| 100 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >0.0218 | |
| أمونيا | 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >0.00974 |
| ثنائي أكسيد الكربون | 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >0.0147 |
| هيليوم | 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >0.0196 |
| هيدروجين | 0 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >0.0090 |
| زئبق | 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >0.0450 |
| أكسجين | 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >0.0203 |
| ستيم | 100 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >0.0130 |
| ماء سائل | 0 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >1.792 |
| 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >1.002 | |
| 37 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >0.6947 | |
| 40 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >0.653 | |
| 100 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >0.282 | |
| دم كامل | 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >3.015 |
| 37 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >2.084 | |
| بلازما الدم | 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >1.810 |
| 37 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >1.257 | |
| كحول إيثيلي | 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >1.20 |
| الميثانول | 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >0.584 |
| زيت (آلة ثقيلة) | 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >660 |
| الزيت (المحرك، SAE 10) | 30 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= lt-phys-4714">200 |
| زيت (زيتون) | 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >138 |
| الجلسرين | 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >1500 |
| عسل | 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >2000-10000 |
| شراب القيقب | 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >2000-3000 |
| الحليب | 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >3.0 |
| زيت (الذرة) | 20 | \ (\ الوقت\ مرات 10 ^ {3}\)» النمط = «محاذاة النص: المركز؛» class= «lt-phys-4714" >65 |
التدفق الصفحي المحصور في الأنابيب: قانون Poiseuille
ما الذي يسبب التدفق؟ الجواب، بشكل غير مفاجئ، هو فرق الضغط. في الواقع، هناك علاقة بسيطة للغاية بين التدفق الأفقي والضغط. معدل\(Q\) التدفق في الاتجاه من الضغط العالي إلى الضغط المنخفض. كلما زاد فرق الضغط بين نقطتين، زاد معدل التدفق. يمكن ذكر هذه العلاقة على النحو التالي:
\[Q = \frac{p_{2} - p_{1}}{R}\]
أين\(p_1\)\(p_2\) توجد الضغوط عند نقطتين، مثل أي من طرفي الأنبوب،\(R\) وهي مقاومة التدفق. \(R\)تشمل المقاومة كل شيء، باستثناء الضغط، الذي يؤثر على معدل التدفق. على سبيل المثال،\(R\) يكون أكبر بالنسبة للأنبوب الطويل مقارنة بالأنبوب القصير. كلما زادت لزوجة السائل، زادت قيمته\(R\). يؤدي الاضطراب إلى زيادة R بشكل كبير، بينما تقل زيادة قطر الأنبوب\(R\).
إذا كانت اللزوجة صفرًا، يكون السائل بلا احتكاك وتكون مقاومة التدفق صفرية أيضًا. عند مقارنة التدفق غير الاحتكاكي في الأنبوب بالتدفق اللزج، كما في الشكل\(\PageIndex{4}\)، نرى أنه بالنسبة للسائل اللزج، تكون السرعة أكبر في منتصف التيار بسبب السحب عند الحدود. يمكننا أن نرى تأثير اللزوجة في لهب موقد بنسن [الجزء (ج)]، على الرغم من أن لزوجة الغاز الطبيعي صغيرة.
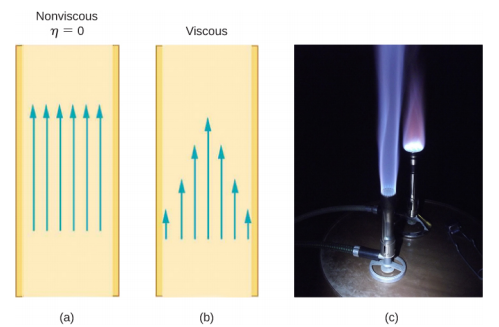
تُعطى المقاومة R للتدفق الصفحي للسائل غير القابل للضغط ذو اللزوجة\(\eta\) عبر أنبوب أفقي بنصف قطر موحد r والطول l، بواسطة
\[R = \frac{8 \eta l}{\pi r^{4}} \ldotp \label{14.18}\]
تُسمى هذه المعادلة بقانون بوايسويل للمقاومة، الذي سُمي على اسم العالم الفرنسي جيه إل بويسوي (1799-1869)، الذي استمدها في محاولة لفهم تدفق الدم عبر الجسم.
دعونا نفحص تعبير Poiseuille عن R لمعرفة ما إذا كان منطقيًا بديهيًا جيدًا. نرى أن المقاومة تتناسب طرديًا مع كل من لزوجة\(\eta\) السائل وطول الأنبوب l. بعد كل شيء، يؤثر كلاهما بشكل مباشر على مقدار الاحتكاك الذي يتم مواجهته - كلما زادت المقاومة وكلما قل التدفق. يؤثر نصف قطر الأنبوب r على المقاومة، وهو أمر منطقي مرة أخرى، لأنه كلما زاد نصف القطر، زاد التدفق (تبقى جميع العوامل الأخرى كما هي). ولكن من المدهش أن يتم رفع r إلى السلطة الرابعة في قانون Poiseuille. هذا الأس يعني أن أي تغيير في نصف قطر الأنبوب له تأثير كبير جدًا على المقاومة. على سبيل المثال، تؤدي مضاعفة نصف قطر الأنبوب إلى تقليل المقاومة بعامل 2 4 = 16.
تؤخذ معًا\(Q = \frac{p_{2} - p_{1}}{R}\)\(R = \frac{8 \eta l}{\pi r^{4}}\) وتعطي التعبير التالي لمعدل التدفق:
\[Q = \frac{(p_{2} - p_{1}) \pi r^{4}}{8 \eta l} \ldotp \label{14.19}\]
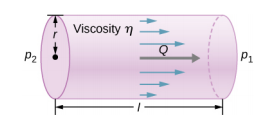
تصف هذه المعادلة التدفق الصفحي عبر الأنبوب. يطلق عليه أحيانًا قانون Poiseuille للتدفق الصفحي، أو ببساطة قانون Poiseuille (الشكل\(\PageIndex{5}\)).
تم تصميم نظام تكييف الهواء لتزويد الهواء بضغط قياسي يبلغ 0.054 باسكال عند درجة حرارة 20 درجة مئوية، ويتم إرسال الهواء عبر قناة دائرية معزولة بقطر 18.00 سم. يبلغ طول القناة 20 مترًا وهي مفتوحة لغرفة عند الضغط الجوي 101.30 كيلو باسكال. يبلغ طول الغرفة 12 مترًا وعرضها 6 أمتار وارتفاعها 3 أمتار. (أ) ما هو معدل تدفق الحجم عبر الأنبوب، بافتراض التدفق الصفحي؟ (ب) تقدير المدة الزمنية لاستبدال الهواء بالكامل في الغرفة. (ج) تقرر شركات البناء توفير المال باستخدام قناة قطرها 9.00 سم. ما هو معدل التدفق الجديد؟
إستراتيجية
بافتراض التدفق الصفحي، ينص قانون Poiseuille على ذلك
\[Q = \frac{(p_{2} - p_{1}) \pi r^{4}}{8 \eta l} = \frac{dV}{dt} \ldotp \nonumber\]
نحتاج إلى مقارنة نصف قطر الشريان قبل وبعد تقليل معدل التدفق. لاحظ أننا أعطينا قطر القناة، لذلك يجب أن نقسم على اثنين للحصول على نصف القطر.
الحل
- بافتراض وجود فرق ثابت في الضغط واستخدام اللزوجة\(\eta = 0.0181\; mPa\; \cdotp s\)، $Q =\ frac {(0.054\؛ Pa) (3.14) (0.09\؛ م) ^ {4}} {8 (0.0181\ مرات 10^ {-3}\؛ Pa\؛\ cdotp s) (20\؛ م)} = 3.84\ مرات 10^ {-3}\\؛ m^ {3} ///ldotp $$
- بافتراض التدفق الثابت\(Q = \frac{dV}{dt} \approx \frac{\Delta V}{\Delta t}\) $$\ Delta t =\ frac {\ دلتا V} {Q} =\ frac {(12\; م) (6\; م) (3\; م)} {3.84\ مرات 10^ {-3}\ m^ {3} /s} = 5.63\ مرات 10^ {4}\; s = 15.63\; ساعة\ ldotp\ nonumber$$
- باستخدام التدفق الصفحي، ينتج قانون Poiseuille $Q =\ frac {(0.054\؛ Pa) (3.14) (0.045\؛ م) {4}} {8 (0.0181\ مرات 10^ {-3}\؛ Pa\؛\ cdotp s) (20\؛ م)} = 22.40\ مرات 10 ^ {-4}\\\؛ m^ {3} /////LDOTP $وهكذا، يقلل نصف قطر القناة بمقدار النصف من معدل التدفق إلى 6.25٪ من القيمة الأصلية.
الأهمية
بشكل عام، بافتراض التدفق الصفحي، فإن تقليل نصف القطر له تأثير أكثر إثارة من تغيير الطول. في حالة زيادة الطول وظلت جميع المتغيرات الأخرى ثابتة، ينخفض معدل التدفق:
\[\begin{split} \frac{Q_{A}}{Q_{B}} & = \frac{\frac{(p_{2} - p_{1}) \pi r_{A}^{4}}{8 \eta l_{A}}}{\frac{(p_{2} - p_{1}) \pi r_{B}^{4}}{8 \eta l_{B}}} = \frac{l_{B}}{l_{A}} \\ Q_{B} & = \frac{l_{A}}{l_{B}} Q_{A} \ldotp \end{split} \nonumber\]
تؤدي مضاعفة الطول إلى خفض معدل التدفق إلى نصف معدل التدفق الأصلي.
إذا انخفض نصف القطر وظلت جميع المتغيرات الأخرى ثابتة، فإن معدل تدفق الحجم ينخفض بعامل أكبر بكثير.
\[\begin{split} \frac{Q_{A}}{Q_{B}} & = \frac{\frac{(p_{2} - p_{1}) \pi r_{A}^{4}}{8 \eta l_{A}}}{\frac{(p_{2} - p_{1}) \pi r_{B}^{4}}{8 \eta l_{B}}} = \left(\dfrac{r_{A}}{r_{B}}\right)^{4} \\ Q_{B} & = \left(\dfrac{r_{B}}{r_{A}}\right)^{4} Q_{A} \end{split}\]
يؤدي قطع نصف القطر إلى النصف إلى تقليل معدل التدفق إلى واحد عشر من معدل التدفق الأصلي.
التدفق والمقاومة كأسباب لانخفاض الضغط
أحيانًا يكون ضغط المياه في المنازل أقل من المعتاد في أوقات الاستخدام الكثيف، مثل أيام الصيف الحارة. يحدث انخفاض الضغط في المياه الرئيسية قبل وصولها إلى المنازل الفردية. دعونا ننظر في التدفق عبر المياه الرئيسية كما هو موضح في الشكل\(\PageIndex{6}\). يمكننا أن نفهم سبب انخفاض الضغط p 1 على المنزل في أوقات الاستخدام الكثيف عن طريق إعادة ترتيب معادلة معدل التدفق:
\[\begin{align} Q & = \frac{p_{2} - p_{1}}{R} \\[4pt] p_{2} - p_{1} & = RQ . \label{EQ5} \end{align}\]
في هذه الحالة،\(p_2\) يكون الضغط عند محطات المياه\(R\) هو مقاومة الماء الرئيسي. في أوقات الاستخدام الكثيف،\(Q\) يكون معدل التدفق كبيرًا. هذا يعني أنه\(p_2 − p_1\) يجب أن يكون كبيرًا أيضًا. وبالتالي\(p_1\) يجب أن تنخفض. من الصحيح التفكير في التدفق والمقاومة على أنهما تسببان في انخفاض الضغط من p 2 إلى p 1. المعادلة p 2 − p 1 = RQ صالحة لكل من التدفقات الصفحية والمضطربة.

يمكننا أيضًا استخدام Equation\ ref {EQ5} لتحليل انخفاضات الضغط التي تحدث في الأنظمة الأكثر تعقيدًا حيث لا يكون نصف قطر الأنبوب هو نفسه في كل مكان. تكون المقاومة أكبر بكثير في الأماكن الضيقة، مثل الشريان التاجي المسدود. بالنسبة لمعدل تدفق معين Q، يكون انخفاض الضغط أكبر عندما يكون الأنبوب أكثر ضيقًا. هذه هي الطريقة التي تتحكم بها صنابير المياه في التدفق. بالإضافة إلى ذلك، يزداد R بشكل كبير بسبب الاضطراب، ويؤدي الانقباض الذي يسبب الاضطراب إلى تقليل الضغط بشكل كبير في اتجاه مجرى النهر. تعمل اللويحات الموجودة في الشريان على تقليل الضغط وبالتالي التدفق، سواء من خلال مقاومتها أو بسبب الاضطراب الذي تسببه.
قياس الاضطراب
\(N_R\)يمكن لمؤشر يسمى رقم رينولدز أن يكشف ما إذا كان التدفق رقائقيًا أم مضطربًا. بالنسبة للتدفق في أنبوب ذي قطر موحد، يتم تعريف رقم رينولدز على أنه
\[N_{R} = \frac{2 \rho vr}{\eta}\; (flow\; in\; tube) \label{14.20}\]
\(\rho\)أين كثافة السائل\(\eta\) وسرعته ولزوجته ونصف قطر\(r\) الأنبوب. رقم رينولدز هو كمية بلا أبعاد. كشفت التجارب أن ذلك\(N_R\) مرتبط ببداية الاضطراب. بالنسبة لـ N R التي تقل عن 2000 تقريبًا، يكون التدفق رقائقيًا. بالنسبة لأكثر\(N_R\) من 3000 تقريبًا، يكون التدفق مضطربًا.
بالنسبة للقيم التي\(N_R\) تتراوح بين 2000 و 3000 تقريبًا، يكون التدفق غير مستقر - أي أنه يمكن أن يكون رقائقيًا، لكن العوائق الصغيرة وخشونة السطح يمكن أن تجعله مضطربًا، وقد يتذبذب عشوائيًا بين كونه رقائقيًا ومضطربًا. في الواقع، يعد تدفق السائل برقم رينولدز بين 2000 و 3000 مثالًا جيدًا على السلوك الفوضوي. يُعرّف النظام بأنه فوضوي عندما يكون سلوكه حساسًا جدًا لبعض العوامل بحيث يصعب للغاية التنبؤ به. من الصعب، ولكن ليس من المستحيل، التنبؤ بما إذا كان التدفق مضطربًا أم لا عندما ينخفض رقم رينولد للسائل في هذا النطاق بسبب الاعتماد الحساس للغاية على عوامل مثل الخشونة والعوائق على طبيعة التدفق. الاختلاف البسيط في عامل واحد له تأثير مبالغ فيه (أو غير خطي) على التدفق.
في المثال 14.8، وجدنا أن معدل تدفق الحجم لنظام تكييف الهواء هو Q = 3.84 × 10 −3 m 3s. افترض هذا الحساب التدفق الصفحي.
- هل كان هذا افتراضًا جيدًا؟
- ما السرعة التي سيصبح بها التدفق مضطربًا؟
إستراتيجية
لتحديد ما إذا كان تدفق الهواء عبر نظام تكييف الهواء رقائقيًا، نحتاج أولاً إلى إيجاد السرعة، والتي يمكن العثور عليها من خلال
\[Q = Av = \pi r^{2} v \ldotp \nonumber\]
ثم يمكننا حساب رقم رينولد، باستخدام المعادلة أدناه، وتحديد ما إذا كان يقع في نطاق التدفق الصفحي
\[R = \frac{2 \rho vr}{\eta} \ldotp \nonumber \]
الحل
- باستخدام القيم المعطاة: $$\ ابدأ {الانقسام} v & =\ frac {Q} {\ pi r^ {2}} =\ frac {3.84\ مرات 10^ {-3}\؛ m^ {3} /s} {3.14 (0.09\؛ م) ^ {2} = 0.15\ م/ث\\ R & =\ frac {2} {\ rho vr} {\ إيتا} = 0.15\ م/ث\\ R & =\ frac {2\ rho vr} {\ إيتا} = c {2 (1.23\; كجم/م ^ {3}) (0.15\; م/ث) (0.09\; م)} {0.0181\ مرات 10^ {-3}\; با\;\ cdotp s} = 1835\ ldotp\ end {الانقسام} $منذ عائلة رينولدز الرقم هو 1835 < 2000، والتدفق رقائقي وليس مضطربًا. الافتراض القائل بأن التدفق كان رقائقيًا صحيح.
- للعثور على السرعة القصوى للهواء للحفاظ على التدفق الصفحي، ضع في اعتبارك رقم رينولد. $$\ ابدأ {الانقسام} R & =\ frac {2\ rho vr} {\ eta}\\ leq 2000\\ v & =\ frac {2000 (0.0181\ مرات 10^ {-3}\؛ باسكال\\ cdotp s)} {2 (1.23\؛ كغم/م^ {3}) (0.09\ م)} = 0.16\؛ م/ث\ ldotp\ end الانقسام} $$
الأهمية
عند نقل السائل من نقطة إلى أخرى، من المستحسن الحد من الاضطراب. يؤدي الاضطراب إلى إهدار الطاقة، حيث تتبدد بعض الطاقة المخصصة لتحريك السائل عند تشكل الدوامات. في هذه الحالة، سيصبح نظام تكييف الهواء أقل كفاءة بمجرد أن تتجاوز السرعة 0.16 متر/ثانية، لأن هذه هي النقطة التي سيبدأ عندها الاضطراب في الحدوث.


