14.8: معادلة برنولي
- Page ID
- 200184
- اشرح المصطلحات في معادلة برنولي
- اشرح كيف ترتبط معادلة برنولي بالحفاظ على الطاقة
- وصف كيفية استخلاص مبدأ بيرنولي من معادلة بيرنولي
- قم بإجراء العمليات الحسابية باستخدام مبدأ برنولي
- وصف بعض تطبيقات مبدأ بيرنولي
كما أوضحنا في الشكل 14.7.4، عندما يتدفق السائل إلى قناة أضيق، تزداد سرعته. وهذا يعني أن طاقتها الحركية تزداد أيضًا. تأتي الطاقة الحركية المتزايدة من العمل الصافي المنجز على السائل لدفعه إلى داخل القناة. أيضًا، إذا تغير السائل في موضعه الرأسي، يتم العمل على السائل بواسطة قوة الجاذبية.
يحدث فرق الضغط عندما تضيق القناة. ينتج عن فرق الضغط هذا قوة صافية على السائل لأن الضغط مضروبًا في المساحة يساوي القوة، وهذه القوة الصافية تعمل. أذكر نظرية الشغل والطاقة،
\[W_{net} = \frac{1}{2} mv^{2} - \frac{1}{2} mv_{0}^{2} \ldotp\]
يزيد العمل الصافي المنجز من الطاقة الحركية للسائل. ونتيجة لذلك، ينخفض الضغط في السائل سريع الحركة سواء كان السائل محصورًا في الأنبوب أم لا.
هناك العديد من الأمثلة الشائعة لانخفاض الضغط في السوائل سريعة الحركة. على سبيل المثال، تتميز ستائر الدش بعادة كريهة تتمثل في الانتفاخ في كشك الدش عند تشغيل الدش. والسبب هو أن تيار الماء والهواء عالي السرعة يخلق منطقة ذات ضغط منخفض داخل الدش، بينما يظل الضغط على الجانب الآخر عند الضغط الجوي القياسي. ينتج عن فرق الضغط هذا قوة صافية تدفع الستارة إلى الداخل. وبالمثل، عندما تمر سيارة بشاحنة على الطريق السريع، يبدو أن المركبتين تتجهان نحو بعضهما البعض. السبب هو نفسه: السرعة العالية للهواء بين السيارة والشاحنة تخلق منطقة من الضغط المنخفض بين المركبات، ويتم دفعها معًا من خلال ضغط أكبر على الخارج (الشكل\(\PageIndex{1}\)). وقد لوحظ هذا التأثير منذ منتصف القرن التاسع عشر، عندما تبين أن القطارات التي تمر في اتجاهين متعاكسين تميل بشكل غير مستقر نحو بعضها البعض.
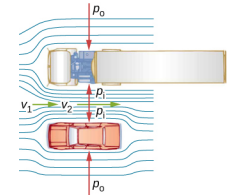
الحفاظ على الطاقة ومعادلة برنولي
يؤدي تطبيق مبدأ الحفاظ على الطاقة على التدفق الصفحي غير الاحتكاكي إلى علاقة مفيدة جدًا بين الضغط وسرعة التدفق في السائل. وتُسمى هذه العلاقة معادلة برنولي، التي سُميت على اسم دانييل بيرنولي (1700-1782)، الذي نشر دراساته عن حركة الموائع في كتابه Hydrodynamica (1738).
ضع في اعتبارك سائلًا غير قابل للضغط يتدفق عبر أنبوب يختلف قطره وارتفاعه، كما هو موضح في الشكل\(\PageIndex{2}\). يشير النصفان 1 و 2 في الشكل إلى موقعين على طول الأنبوب ويوضحان العلاقات بين مناطق المقاطع العرضية A، وسرعة التدفق v، والارتفاع من الأرض y، والضغط p عند كل نقطة. نفترض هنا أن الكثافة عند النقطتين هي نفسها - وبالتالي، يتم الإشارة إلى الكثافة\(\rho\) بدون أي رموز فرعية - وبما أن السائل غير قابل للضغط، يجب أن تكون الأحجام المظللة متساوية.
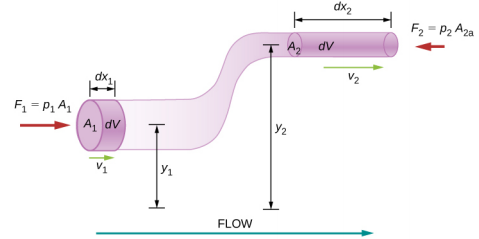
نفترض أيضًا أنه لا توجد قوى لزجة في السائل، لذلك سيتم الحفاظ على طاقة أي جزء من السائل. لاشتقاق معادلة برنولي، نحسب أولاً العمل الذي تم إجراؤه على السائل:
\[\begin{split} dW & = F_{1} dx_{1} - F_{2} dx_{2} \\ & = p_{1} A_{1} dx_{1} - p_{2} A_{2} dx_{2} \\ & = p_{1} dV - p_{2} dV = (p_{1} - p_{2}) dV \ldotp \end{split}\]
كان العمل المنجز بسبب القوة المحافظة للجاذبية والتغير في الطاقة الحركية للسائل. التغيير في الطاقة الحركية للسائل يساوي
\[dK = \frac{1}{2} m_{2} v_{2}^{2} - \frac{1}{2} m_{1} v_{1}^{2} = \frac{1}{2} \rho dV (v_{2}^{2} - v_{1}^{2}) \ldotp\]
التغيير في الطاقة الكامنة هو
\[dU = mgy_{2} - mgy_{1} = \rho dV g(y_{2} - y_{1}) \ldotp\]
ثم تصبح معادلة الطاقة
\[\begin{split} dW & = dK + dU \\ (p_{1} - p_{2}) dV & = \frac{1}{2} \rho dV (v_{2}^{2} - v_{1}^{2}) + \rho dV g(y_{2} - y_{1}) \\ (p_{1} - p_{2}) & = \frac{1}{2} \rho (v_{2}^{2} - v_{1}^{2}) + \rho g(y_{2} - y_{1}) \ldotp \end{split}\]
إعادة ترتيب المعادلة تعطي معادلة برنولي:
\[p_{1} + \frac{1}{2} \rho v_{1}^{2} + \rho gy_{1} = p_{2} + \frac{1}{2} \rho v_{2}^{2} + \rho gy_{2} \ldotp\]
تنص هذه العلاقة على أن الطاقة الميكانيكية لأي جزء من السائل تتغير نتيجة العمل الذي يقوم به السائل الخارجي لذلك الجزء، بسبب الضغط المتغير على طول الطريق. نظرًا لاختيار النقطتين بشكل تعسفي، يمكننا كتابة معادلة برنولي بشكل عام كمبدأ للحفظ على طول التدفق.
بالنسبة للسائل غير القابل للضغط وغير القابل للاحتكاك، يكون مزيج الضغط ومجموع كثافات الطاقة الحركية والمحتملة ثابتًا ليس فقط بمرور الوقت، ولكن أيضًا على طول المسار:
\[p + \frac{1}{2} \rho v^{2} + \rho gy = constant \label{14.16}\]
يجب الإشارة هنا بشكل خاص إلى حقيقة أنه في الحالة الديناميكية، قد تختلف الضغوط عند نفس الارتفاع في أجزاء مختلفة من السائل إذا كانت لها سرعات تدفق مختلفة.
تحليل معادلة بيرنولي
وفقًا لمعادلة برنولي، إذا اتبعنا حجمًا صغيرًا من السائل على طول مساره، فقد تتغير الكميات المختلفة في المجموع، لكن الإجمالي يظل ثابتًا. معادلة برنولي هي، في الواقع، مجرد بيان ملائم للحفاظ على الطاقة لسائل غير قابل للضغط في غياب الاحتكاك.
يحتوي الشكل العام لمعادلة برنولي على ثلاثة مصطلحات، وهو قابل للتطبيق على نطاق واسع. لفهمها بشكل أفضل، دعونا نفكر في بعض المواقف المحددة التي تبسط وتوضح استخدامها ومعناها.
معادلة برنولي للسوائل الساكنة
ضع في اعتبارك أولاً الموقف البسيط للغاية الذي يكون فيه السائل ثابتًا - أي\(v_1 = v_2 = 0\). معادلة برنولي في هذه الحالة هي
\[p_{1} + \rho gh_{1} = p_{2} + \rho gh_{2} \ldotp\]
يمكننا زيادة تبسيط المعادلة عن طريق ضبط h 2 = 0. (يمكن اختيار أي ارتفاع لارتفاع مرجعي قدره صفر، كما هو الحال غالبًا في الحالات الأخرى التي تنطوي على قوة الجاذبية، مما يجعل جميع الارتفاعات الأخرى نسبية.) في هذه الحالة، نحصل على
\[p_{2} = p_{1} + \rho gh_{1} \ldotp\]
تخبرنا هذه المعادلة أنه في السوائل الساكنة، يزداد الضغط مع العمق. عندما ننتقل من النقطة 1 إلى النقطة 2 في السائل، يزداد العمق بمقدار h 1، وبالتالي، يكون p 2 أكبر من p 1 بمقدار\(\rho gh_1\). في أبسط الحالات، ص 1 هو صفر في الجزء العلوي من السائل، ونحصل على العلاقة المألوفة\(p = \rho gh\). (أذكر أن p =\(\rho gh\) و\(\Delta Ug = −mgh\).) وهكذا، تؤكد معادلة برنولي حقيقة أن تغير الضغط بسبب وزن السائل هو\(\rho gh\). على الرغم من أننا نقدم معادلة برنولي لحركة الموائع، إلا أنها تتضمن الكثير مما درسناه للسوائل الساكنة سابقًا.
مبدأ بيرنولي
لنفترض أن السائل يتحرك ولكن عمقه ثابت - أي\(h_1 = h_2\). في ظل هذه الحالة، تصبح معادلة برنولي
\[p_{1} + \frac{1}{2} \rho v_{1}^{2} = p_{2} + \frac{1}{2} \rho v_{2}^{2} \ldotp \label{Bernoulli}\]
تعتبر الحالات التي يتدفق فيها السائل على عمق ثابت شائعة جدًا لدرجة أن هذه المعادلة غالبًا ما تسمى أيضًا مبدأ برنولي، وهو ببساطة معادلة برنولي للسوائل عند عمق ثابت. (لاحظ مرة أخرى أن هذا ينطبق على حجم صغير من السوائل بينما نتبعه على طول مساره.) يعزز مبدأ برنولي حقيقة أن الضغط ينخفض مع زيادة السرعة في السائل المتحرك: إذا كانت v 2 أكبر من v 1 في المعادلة، فيجب أن تكون p 2 أقل من p 1 حتى تصمد المساواة.
في المثال 14.5، وجدنا أن سرعة الماء في خرطوم زادت من 1.96 متر/ثانية إلى 25.5 m/s أثناء الانتقال من الخرطوم إلى الفوهة. احسب الضغط في الخرطوم، علمًا بأن الضغط المطلق في الفوهة يساوي 1.01 × 10 5 نيوتن/م 2 (الغلاف الجوي، كما يجب أن يكون) وبافتراض مستوى التدفق الخالي من الاحتكاك.
إستراتيجية
التدفق المستوي يعني عمقًا ثابتًا، لذلك ينطبق مبدأ برنولي. نحن نستخدم الحرف 1 للقيم في المنزل و 2 لتلك الموجودة في الفوهة. لذلك يُطلب منا العثور على ص 1.
الحل
حل مبدأ بيرنولي (معادلة برنولي)\(p_1\) للعوائد
\[ \begin{align*} p_{1} &= p_{2} \frac{1}{2} \rho v_{2}^{2} - \frac{1}{2} \rho v_{1}^{2} \\[4pt] &= p_{2} + \frac{1}{2} \rho (v_{2}^{2} - v_{1}^{2}) \ldotp \end{align*}\]
استبدال القيم المعروفة،
\[\begin{align*} p_{1} & = (1.01 \times 10^{5}\; N/m^{2}) + \frac{1}{2} (10^{3}\; kg/m^{3})[(25.5\; m/s)^{2} - (1.96\; m/s)^{2}] \\[4pt] & = 4.24 \times 10^{5}\; N/m^{2} \ldotp \end{align*}\]
الدلالة
هذا الضغط المطلق في الخرطوم أكبر منه في الفوهة، كما هو متوقع، حيث أن v أكبر في الفوهة. يجب أن يكون الضغط p 2 في الفوهة في الغلاف الجوي، لأن الماء يخرج إلى الغلاف الجوي دون تغييرات أخرى في الظروف.
تطبيقات مبدأ بيرنولي
تحدث العديد من الأجهزة والمواقف التي يتدفق فيها السائل على ارتفاع ثابت وبالتالي يمكن تحليله وفقًا لمبدأ برنولي.
إنتراينمنت
لطالما استخدم الناس مبدأ برنولي للعمل باستخدام الضغط المنخفض في السوائل عالية السرعة لتحريك الأشياء. مع ارتفاع الضغط من الخارج، يدفع السائل عالي السرعة السوائل الأخرى إلى التيار. هذه العملية تسمى الإنتراينمنت. تم استخدام أجهزة الصرف الصحي منذ العصور القديمة كمضخات لرفع المياه إلى ارتفاعات صغيرة، كما هو ضروري لتجفيف المستنقعات أو الحقول أو غيرها من المناطق المنخفضة. يوضح الشكل بعض الأجهزة الأخرى التي تستخدم مفهوم التنصيب\(\PageIndex{3}\).
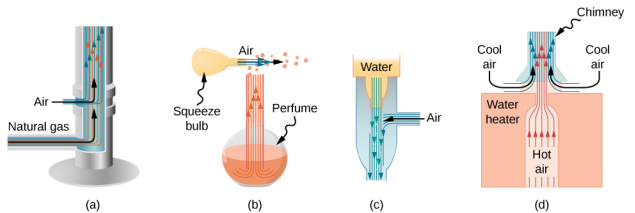
قياس السرعة
\(\PageIndex{4}\)يوضِّح الشكل جهازين يطبِّقان مبدأ برنولي لقياس سرعة الموائع. يتم توصيل جهاز قياس الضغط في الجزء (أ) بأنبوبين صغيرين بما يكفي لعدم إزعاج التدفق بشكل ملحوظ. يخلق الأنبوب المواجه للسائل القادم بقعة ميتة ذات سرعة صفرية (v 1 = 0) أمامه، بينما السائل الذي يمر بالأنبوب الآخر له سرعة v 2. هذا يعني أن مبدأ برنولي كما هو مذكور في
\[p_{1} + \frac{1}{2} \rho v_{1}^{2} = p_{2} + \frac{1}{2} \rho v_{2}^{2}\]
يصبح
\[p_{1} = p_{2} + \frac{1}{2} \rho v_{2}^{2} \ldotp\]
وبالتالي يتم تقليل الضغط p 2 فوق الفتحة الثانية بمقدار h\(\frac{1}{2} \rho v_{2}^{2}\)، وبالتالي يرتفع السائل الموجود في مقياس الضغط بمقدار h على الجانب المتصل بالفتحة الثانية، حيث
\[h \propto \frac{1}{2} \rho v_{2}^{2} \ldotp\]
(تذكر أن الرمز\(\propto\) يعني «يتناسب مع».) حل الإصدار 2، نرى ذلك
\[v_{2} \propto \sqrt{h} \ldotp\]
يعرض الجزء (ب) إصدارًا من هذا الجهاز شائع الاستخدام لقياس سرعات السوائل المختلفة؛ وتستخدم هذه الأجهزة بشكل متكرر كمؤشرات للسرعة الجوية في الطائرات.
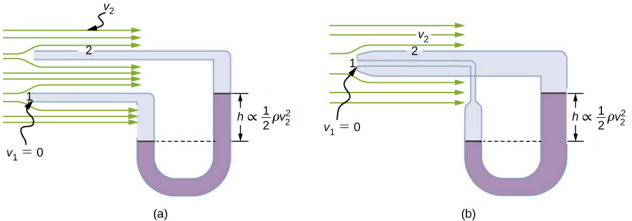
خرطوم إطفاء
تضمنت جميع التطبيقات السابقة لمعادلة برنولي تبسيط الشروط، مثل الارتفاع الثابت أو الضغط المستمر. المثال التالي هو تطبيق أكثر عمومية لمعادلة برنولي حيث يتغير كل من الضغط والسرعة والارتفاع.
يبلغ قطر خراطيم الحريق المستخدمة في الحرائق الهيكلية الرئيسية 6.40 سم (الشكل\(\PageIndex{5}\)). لنفترض أن هذا الخرطوم يحمل تدفقًا قدره 40.0 لتر/ثانية، بدءًا من ضغط قياس 1.62 × 10 6 نيوتن/م 2. يرتفع الخرطوم لمسافة 10.0 أمتار على طول السلم إلى فوهة يبلغ قطرها الداخلي 3.00 سم. ما هو الضغط في الفوهة؟

إستراتيجية
يجب أن نستخدم معادلة برنولي لحل الضغط، لأن العمق ليس ثابتًا.
الحل
معادلة بيرنولي هي
\[p_{1} + \frac{1}{2} \rho v_{1}^{2} + \rho gh_{1} = p_{2} + \frac{1}{2} \rho v_{2}^{2} + \rho gh_{2} \nonumber \]
حيث يشير النصان 1 و 2 إلى الظروف الأولية عند مستوى الأرض والظروف النهائية داخل الفوهة، على التوالي. يجب علينا أولاً العثور على السرعات v 1 و v 2. بما أن Q = A 1 v 1، نحصل على
\[v_{1} = \frac{Q}{A_{1}} = \frac{40.0 \times 10^{-3}\; m^{3}/s}{\pi (3.20 \times 10^{-2}\; m)^{2}} = 12.4\; m/s \ldotp \nonumber\]
وبالمثل، نجد
\[v_{2} = 56.6\; m/s \ldotp \nonumber\]
هذه السرعة الكبيرة تساعد في الوصول إلى النار. الآن، بأخذ h 1 لتكون صفرًا، نحل معادلة برنولي للصع 2:
\[p_{2} = p_{1} + \frac{1}{2} \rho (v_{1}^{2} - v_{2}^{2}) - \rho gh_{2} \ldotp \nonumber\]
استبدال عوائد القيم المعروفة
\[\begin{align*} p_{2} & = (1.62 \times 10^{6}\; N/m^{2}) + \frac{1}{2} (1000\; kg/m^{3}) [(12.4\; m/s)^{2} - (56.6\; m/s)^{2}] - (1000\; kg/m^{3})(9.80\; m/s^{2})(10.0\; m) \\ & = 0 \ldotp \end{align*}\]
الدلالة
هذه القيمة هي ضغط المقياس، حيث تم إعطاء الضغط الأولي كضغط قياس. وبالتالي، فإن ضغط الفوهة يساوي الضغط الجوي كما يجب، لأن الماء يخرج إلى الغلاف الجوي دون تغيير في ظروفه.


