14.7: ديناميكا السوائل
- Page ID
- 200177
- وصف خصائص التدفق
- حساب معدل التدفق
- وصف العلاقة بين معدل التدفق والسرعة
- شرح عواقب معادلة الاستمرارية للحفاظ على الكتلة
تناول الجزء الأول من هذا الفصل إحصائيات الموائع، ودراسة السوائل أثناء الراحة. يتناول الجزء المتبقي من هذا الفصل ديناميكيات الموائع، ودراسة السوائل المتحركة. حتى الأشكال الأساسية لحركة السوائل يمكن أن تكون معقدة للغاية. لهذا السبب، نقتصر بحثنا على السوائل المثالية في العديد من الأمثلة. السائل المثالي هو سائل ذو لزوجة ضئيلة. اللزوجة هي مقياس للاحتكاك الداخلي في السائل؛ نقوم بفحصه بمزيد من التفصيل في اللزوجة والاضطراب. في بعض الأمثلة، نفحص سائلًا غير قابل للضغط - سائل يتطلب قوة كبيرة جدًا لتغيير الحجم - نظرًا لأن الكثافة في السائل غير القابل للضغط ثابتة طوال الوقت.
خصائص التدفق
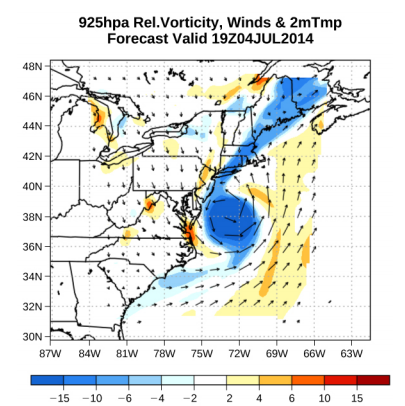
غالبًا ما تستخدم متجهات السرعة لتوضيح حركة السوائل في تطبيقات مثل الأرصاد الجوية. على سبيل المثال، يمكن تمثيل الرياح - حركة السوائل للهواء في الغلاف الجوي - بواسطة متجهات تشير إلى سرعة واتجاه الرياح في أي نقطة معينة على الخريطة. \(\PageIndex{1}\)يوضح الشكل متجهات السرعة التي تصف الرياح خلال إعصار آرثر في عام 2014.
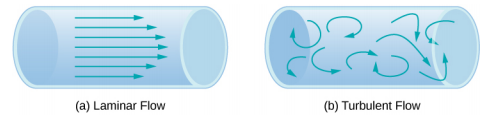
طريقة أخرى لتمثيل حركة السوائل هي التبسيط. يمثل الانسياب مسار حجم صغير من السائل أثناء تدفقه. تكون السرعة دائمًا عرضية للانسيابية. \(\PageIndex{2}\)تستخدم المخططات في الشكل خطوطًا مبسطة لتوضيح مثالين للسوائل التي تتحرك عبر الأنبوب. يُظهر السائل الأول تدفقًا رقائقيًا (يوصف أحيانًا بأنه تدفق ثابت)، يمثله خطوط انسيابية متوازية سلسة. لاحظ أنه في المثال الموضح في الجزء (أ)، تكون سرعة السائل أكبر في المركز وتنخفض بالقرب من جدران الأنبوب بسبب لزوجة السائل والاحتكاك بين جدران الأنابيب والسائل. هذه حالة خاصة من التدفق الصفحي، حيث يكون الاحتكاك بين الأنبوب والسائل مرتفعًا، والمعروف باسم ظروف عدم الانزلاق. يمثل المخطط الثاني التدفق المضطرب، حيث تكون الخطوط الانسيابية غير منتظمة وتتغير بمرور الوقت. في حالة التدفق المضطرب، تكون مسارات تدفق السوائل غير منتظمة حيث تختلط أجزاء مختلفة من السائل معًا أو تشكل مناطق دائرية صغيرة تشبه الدوامات. يمكن أن يحدث هذا عندما تصل سرعة السائل إلى سرعة حرجة معينة.
معدل التدفق وعلاقته بالسرعة
يُطلق على حجم السائل الذي يمر بموقع معين عبر منطقة ما خلال فترة زمنية اسم معدل التدفق\(Q\)، أو بشكل أكثر دقة، معدل تدفق الحجم. في الرموز، تتم كتابة هذا كـ
\[Q = \frac{dV}{dt} \label{14.13}\]
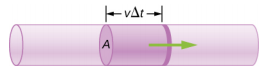
أين\(V\) الحجم\(t\) وهو الوقت المنقضي. في الشكل\(\PageIndex{3}\)، حجم الأسطوانة هو\(Ax\)، وبالتالي فإن معدل التدفق هو
\[Q = \frac{dV}{dt} = \frac{d}{dt} (Ax) = A \frac{dx}{dt} = Av \ldotp\]
وحدة SI لمعدل التدفق هي m 3/s، ولكن\(Q\) هناك عدة وحدات أخرى شائعة الاستخدام، مثل اللترات في الدقيقة (L/دقيقة). لاحظ أن اللتر (L) يساوي 1/1000 من المتر المكعب أو 1000 سنتيمتر مكعب (10 −3 م 3 أو 10 3 سم 3).
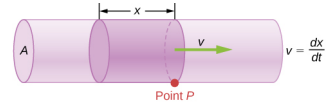
يرتبط معدل التدفق والسرعة بكميات فيزيائية ولكنها مختلفة تمامًا. لتوضيح التمييز، ضع في اعتبارك معدل تدفق النهر. كلما زادت سرعة الماء، زاد معدل تدفق النهر. لكن معدل التدفق يعتمد أيضًا على حجم وشكل النهر. على سبيل المثال، يحمل تيار جبلي سريع كميات أقل بكثير من المياه مقارنة بنهر الأمازون في البرازيل. \(\PageIndex{3}\)يوضح الشكل معدل تدفق الحجم. معدل تدفق الحجم هو\(Q = \frac{dV}{dt} = Av\)، حيث A هي مساحة المقطع العرضي للأنبوب و v هي حجم السرعة.
العلاقة الدقيقة بين معدل التدفق\(Q\) ومتوسط السرعة\(v\) هي
\[Q = Av,\]
\(A\)أين منطقة المقطع العرضي\(v\) وهي السرعة المتوسطة. تخبرنا العلاقة أن معدل التدفق يتناسب طرديًا مع كل من متوسط سرعة السائل ومساحة المقطع العرضي للنهر أو الأنبوب أو القناة الأخرى. كلما كبرت القناة، زادت مساحة المقطع العرضي لها. \(\PageIndex{3}\)يوضح الشكل كيفية الحصول على هذه العلاقة. تحتوي الأسطوانة المظللة على حجم\(V = Ad\) يتدفق بعد النقطة\(P\) في كل مرة\(t\). تقسيم جانبي هذه العلاقة\(t\) بالعطاء
\[\frac{V}{t} = \frac{Ad}{t} \ldotp \label{eq14.14A} \]
نلاحظ ذلك\(Q = \frac{V}{t}\) ومتوسط السرعة هو\(v = \frac{d}{t}\). وهكذا تصبح المعادلة\ المرجع {eQ14.14a}
\[Q = Av.\]
\(\PageIndex{4}\)يوضح الشكل سائلًا غير قابل للضغط يتدفق على طول أنبوب نصف قطره المتناقص. نظرًا لأن السائل غير قابل للضغط، يجب أن تتدفق نفس كمية السائل بعد أي نقطة في الأنبوب في وقت معين لضمان استمرارية التدفق. يكون التدفق مستمرًا نظرًا لعدم وجود مصادر أو أحواض تضيف الكتلة أو تزيلها، لذلك يجب أن تكون الكتلة المتدفقة إلى الأنبوب مساوية للكتلة المتدفقة من الأنبوب. في هذه الحالة، نظرًا لانخفاض مساحة المقطع العرضي للأنبوب، يجب بالضرورة زيادة السرعة. يمكن توسيع هذا المنطق ليقول أن معدل التدفق يجب أن يكون هو نفسه في جميع النقاط على طول الأنبوب. على وجه الخصوص، بالنسبة للنقطتين التعسفيتين 1 و 2
\[\begin{split} Q_{1} & = Q_{2}, \\ A_{1} v_{1} & = A_{2} v_{2} \ldotp \end{split} \label{14.14}\]
وهذا ما يسمى بمعادلة الاستمرارية وهو صالح لأي سائل غير قابل للضغط (بكثافة ثابتة). يمكن ملاحظة عواقب معادلة الاستمرارية عندما يتدفق الماء من خرطوم إلى فوهة رش ضيقة: تخرج بسرعة كبيرة - وهذا هو الغرض من الفوهة. على العكس من ذلك، عندما يصب النهر في أحد طرفي الخزان، يتباطأ الماء بشكل كبير، وربما تزداد سرعته مرة أخرى عندما يغادر الطرف الآخر من الخزان. بمعنى آخر، تزداد السرعة عندما تنخفض مساحة المقطع العرضي، وتنخفض السرعة عندما تزداد مساحة المقطع العرضي.
نظرًا لأن السوائل غير قابلة للضغط بشكل أساسي، فإن معادلة الاستمرارية صالحة لجميع السوائل. ومع ذلك، فإن الغازات قابلة للانضغاط، لذلك يجب تطبيق المعادلة بحذر على الغازات إذا تعرضت للضغط أو التمدد.
يتم توصيل فوهة بقطر 0.500 سم بخرطوم حديقة نصف قطر 0.900 سم. يبلغ معدل التدفق عبر الخرطوم والفوهة 0.500 لتر/ثانية، احسب سرعة الماء:
- في المنزل و
- في الفوهة.
إستراتيجية
يمكننا استخدام العلاقة بين معدل التدفق والسرعة للعثور على كلتا السرعتين. نحن نستخدم الحرف 1 للخرطوم و 2 للفوهة.
الحل
- نحل معادلة معدل التدفق للسرعة ونستخدمها في منطقة المقطع العرضي\(\pi r_{1}^{2}\) للخرطوم، ونحصل على $v =\ frac {Q} {A} =\ frac {Q} {\ pi r_ {1} ^ {2}}\ ldotp$$ قيم الاستبدال واستخدام تحويلات الوحدات المناسبة ينتج $$v =\ frac {(0.500\; l/s) (10^ {-3}\; m^ {3} /L)} {(3.14) (9.00\ مرات 10^ {-3}\؛ م) ^ {2} } = 1.96\؛ م/ث\ ldotp$$
- يمكننا تكرار هذا الحساب لإيجاد السرعة في الفوهة v 2، لكننا نستخدم معادلة الاستمرارية لإعطاء رؤية مختلفة إلى حد ما. تنص المعادلة على $A_ {1} v_ {1} = A_ {2} v_ {2} v_ {2}\ lDotP$$حل v 2 والاستعاضة\(\pi r^{2}\) عن عوائد مساحة المقطع العرضي $$v_ {2} =\ frac {A_ {1}} {A_ {2}} v_ {1} = {1} {1} {\ pi {2} {1} {\ pi {2} {\ pi {2}} {1}} ^ {2} v_ {1} =\ frac {r_ {1} ^ {2}} {r_ {2} ^ {2}} v_ {1}\ ldotp$$ استبدال القيم المعروفة، $v_ {2} =\ فراك {(0.900\؛ سم) ^ {2} {(0.250\؛ سم) ^ {2}} (1.96\؛ م/ث) = 25.5\؛ م/ث\ ldotp$$
الدلالة
سرعة 1.96 متر/ثانية مناسبة تقريبًا للمياه الخارجة من خرطوم بدون فوهة. تنتج الفوهة تيارًا أسرع بكثير بمجرد تقييد التدفق إلى أنبوب أضيق.
يوضح حل الجزء الأخير من المثال أن السرعة تتناسب عكسيًا مع مربع نصف قطر الأنبوب، مما يؤدي إلى تأثيرات كبيرة عندما يتغير نصف القطر. يمكننا إطفاء شمعة من مسافة بعيدة، على سبيل المثال، عن طريق متابعة شفاهنا، في حين أن النفخ على شمعة وفمنا مفتوح على مصراعيه أمر غير فعال تمامًا.
الحفظ الشامل
يمكن أيضًا وصف معدل تدفق السائل من خلال معدل تدفق الكتلة أو معدل التدفق الكتلي. هذا هو المعدل الذي تتحرك به كتلة السائل بعد النقطة. ارجع مرة أخرى إلى الشكل\(\PageIndex{3}\)، ولكن هذه المرة ضع في اعتبارك الكتلة في المجلد المظلل. يمكن تحديد الكتلة من الكثافة والحجم:
\[m = \rho V = \rho Ax \ldotp\]
ثم يكون معدل تدفق الكتلة
\[\frac{dm}{dt} = \frac{d}{dt} (\rho Ax) = \rho A \frac{dx}{dt} = \rho Av,\]
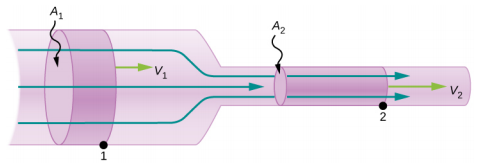
أين\(\rho\) الكثافة، A هي مساحة المقطع العرضي، و v هي حجم السرعة. يعد معدل تدفق الكتلة كمية مهمة في ديناميكيات الموائع ويمكن استخدامه لحل العديد من المشكلات. ضع في اعتبارك الشكل\(\PageIndex{5}\). يبدأ الأنبوب الموجود في الشكل عند المدخل بمساحة مقطع عرضي A 1 ويضيق إلى مخرج بمساحة مقطعية أصغر من A 2. يجب أن تكون كتلة السائل الذي يدخل الأنبوب مساوية لكتلة السائل الخارج من الأنبوب. لهذا السبب تكون السرعة عند المخرج (v 2) أكبر من سرعة المدخل (v 1). باستخدام حقيقة أن كتلة السائل الذي يدخل الأنبوب يجب أن تكون مساوية لكتلة السائل الخارج من الأنبوب، يمكننا إيجاد علاقة بين السرعة ومنطقة المقطع العرضي عن طريق أخذ معدل تغير الكتلة الداخلة والكتلة الخارجة:
\[\begin{split} \left(\dfrac{dm}{dt}\right)_{1} & = \left(\dfrac{dm}{dt}\right)_{2} \\ \rho_{1} A_{1} v_{1} & = \rho_{2} A_{2} v_{2} \ldotp \end{split} \label{14.15}\]
تُعرف المعادلة\ ref {14.15} أيضًا باسم معادلة الاستمرارية في الشكل العام. إذا ظلت كثافة السائل ثابتة خلال الانقباض - أي أن السائل غير قابل للضغط - فإن الكثافة تختفي من معادلة الاستمرارية،
\[A_{1} v_{1} = A_{2} v_{2} \ldotp\]
تنخفض المعادلة لإظهار أن معدل تدفق الحجم في الأنبوب يساوي معدل تدفق الحجم خارج الأنبوب.