14.6: مبدأ أرخميدس والطفو
- Page ID
- 200191
- تعريف قوة الطفو
- مبدأ أرخميدس
- وصف العلاقة بين الكثافة ومبدأ أرخميدس
عند وضعها في سائل، تطفو بعض الأجسام بسبب قوة الطفو. من أين تأتي هذه القوة الطافية؟ لماذا تطفو بعض الأشياء والبعض الآخر لا؟ هل تحصل الأجسام التي تغرق على أي دعم على الإطلاق من السائل؟ هل يتأثر جسمك بالغلاف الجوي، أم أن بالونات الهيليوم فقط هي التي تتأثر (الشكل\(\PageIndex{1}\))؟

تعتمد الإجابات على كل هذه الأسئلة، والعديد من الأسئلة الأخرى، على حقيقة أن الضغط يزداد مع العمق في السائل. هذا يعني أن القوة الصاعدة في الجزء السفلي من الجسم في السائل أكبر من القوة الهابطة أعلى الجسم. توجد قوة تصاعدية أو قوة طفو على أي جسم في أي سائل (الشكل\(\PageIndex{2}\)). إذا كانت قوة الطفو أكبر من وزن الجسم، يرتفع الجسم إلى السطح ويطفو. إذا كانت قوة الطفو أقل من وزن الجسم، فإن الجسم يغرق. إذا كانت قوة الطفو تساوي وزن الجسم، فيمكن أن يظل الجسم معلقًا في عمقه الحالي. تكون قوة الطفو موجودة دائمًا، سواء كان الجسم يطفو أو يغرق أو يتم تعليقه في سائل.
قوة الطفو هي القوة الصاعدة على أي جسم في أي سائل.
مبدأ أرخميدس
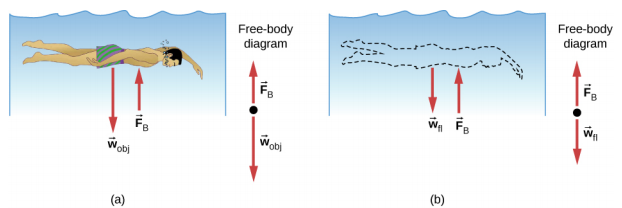
ما حجم قوة الطفو؟ للإجابة على هذا السؤال، فكر فيما يحدث عند إزالة كائن مغمور من السائل، كما هو موضح في الشكل\(\PageIndex{3}\). إذا لم يكن الجسم موجودًا في السائل، فسيتم ملء المساحة التي يشغلها الجسم بسائل وزنه w fl. يتم دعم هذا الوزن بواسطة السائل المحيط، لذلك يجب أن تساوي قوة الطفو w fl، وزن السائل الذي أزاحه الجسم.
قوة الطفو على الجسم تساوي وزن السائل الذي يزيحه. في شكل المعادلة، مبدأ أرخميدس هو
\[F_{B} = w_{fl},\]
حيث F B هي قوة الطفو و w fl هو وزن السائل الذي أزاحه الجسم.
تمت تسمية هذا المبدأ على اسم عالم الرياضيات والمخترع اليوناني أرخميدس (حوالي 287-212 قبل الميلاد)، الذي ذكر هذا المبدأ قبل وقت طويل من ترسيخ مفاهيم القوة.
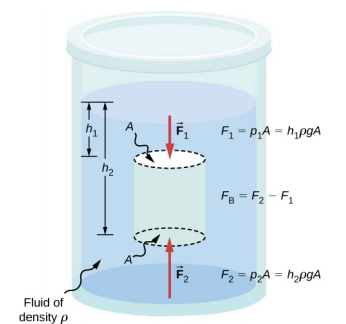
يشير مبدأ أرخميدس إلى قوة الطفو التي تنتج عندما يكون الجسم مغمورًا في سائل، سواء جزئيًا أو كليًا. تؤثر القوة التي توفر ضغط السائل على الجسم بشكل عمودي على سطح الجسم. بعبارة أخرى، يتم توجيه القوة الناتجة عن الضغط في الجزء السفلي لأعلى، بينما في الجزء العلوي، يتم توجيه القوة الناتجة عن الضغط لأسفل؛ تشير القوى الناتجة عن الضغوط على الجانبين إلى الجسم.
نظرًا لأن الجزء السفلي من الجسم يقع على عمق أكبر من الجزء العلوي من الجسم، فإن الضغط في الجزء السفلي من الجسم أعلى من الضغط في الجزء العلوي، كما هو موضح في الشكل\(\PageIndex{2}\). لذلك تعمل القوة الصاعدة الصافية على الجسم. هذه القوة الصاعدة هي قوة الطفو، أو ببساطة الطفو.
غالبًا ما يُنسب التعجب «Eureka» (بمعنى «لقد وجدتها») إلى أرخميدس أثناء قيامه بالاكتشاف الذي من شأنه أن يؤدي إلى مبدأ أرخميدس. يقول البعض أن كل شيء بدأ في حوض الاستحمام. لقراءة القصة، استكشف Scientific American لمعرفة المزيد.
الكثافة ومبدأ أرخميدس
إذا أسقطت كتلة من الطين في الماء، فسوف تغرق. ولكن إذا قمت بتشكيل نفس كتلة الطين على شكل قارب، فسوف تطفو. بسبب شكله، يزيح القارب الطيني كمية أكبر من الماء مقارنة بالكتلة ويختبر قوة طفو أكبر، على الرغم من أن كتلته هي نفسها. وينطبق الشيء نفسه على السفن الفولاذية.
متوسط كثافة الكائن هو ما يحدد في النهاية ما إذا كان يطفو. إذا كان متوسط كثافة الجسم أقل من السائل المحيط، فسوف يطفو. والسبب هو أن السائل، ذو الكثافة العالية، يحتوي على كتلة أكبر وبالتالي المزيد من الوزن في نفس الحجم. وبالتالي فإن قوة الطفو، التي تساوي وزن السائل الذي تم إزاحته، أكبر من وزن الجسم. وبالمثل، سيغرق جسم أكثر كثافة من السائل.
يعتمد مدى غمر الجسم العائم على كيفية مقارنة كثافة الكائن بكثافة السائل. في الشكل\(\PageIndex{4}\)، على سبيل المثال، تكون السفينة التي تم تفريغها ذات كثافة أقل وأقل غمرًا مقارنة بالسفينة نفسها عند تحميلها. يمكننا استخلاص تعبير كمي للكسر المغمور من خلال النظر في الكثافة. الكسر المغمور هو نسبة الحجم المغمور إلى حجم الكائن، أو
\[fraction\; submerged = \frac{V_{sub}}{V_{obj}} = \frac{V_{fl}}{V_{obj}} \ldotp\]
الحجم المغمور يساوي حجم السائل الذي تم إزاحته، والذي نسميه V fl. الآن يمكننا الحصول على العلاقة بين الكثافات عن طريق الاستبدال\(\rho = \frac{m}{V}\) في التعبير. هذا يعطي
\[\frac{V_{fl}}{V_{obj}} = \frac{\frac{m_{fl}}{\rho_{fl}}}{\frac{m_{obj}}{\rho_{obj}}},\]
\(\rho_{obj}\)أين متوسط كثافة الكائن\(\rho_{fl}\) وهي كثافة السائل. نظرًا لأن الجسم يطفو، فإن كتلته وكتلة السائل المُزاح متساويتان، لذا يتم إلغاؤهما من المعادلة، تاركًا
\[fraction\; submerged = \frac{\rho_{obj}}{\rho_{fl}} \ldotp\]
يمكننا استخدام هذه العلاقة لقياس الكثافة.

لنفترض أن امرأة تزن 60.0 كجم تطفو في المياه العذبة مع غمر 97.0٪ من حجمها عندما تمتلئ رئتيها بالهواء. ما هو متوسط كثافتها؟
إستراتيجية
يمكننا إيجاد كثافة المرأة من خلال حل المعادلة
\[fraction\; submerged = \frac{\rho_{obj}}{\rho_{fl}}\]
لكثافة الكائن. هذه العوائد
\[\rho_{obj} = \rho_{person} = (fraction\; submerged) \cdotp \rho_{fl} \ldotp\]
نحن نعرف كل من نسبة المياه المغمورة وكثافة المياه، حتى نتمكن من حساب كثافة المرأة.
الحل
عند إدخال القيم المعروفة في التعبير عن كثافتها، نحصل عليها
\[\rho_{person} = 0.970 \cdotp 10^{3}\; kg/m^{3} = 970\; kg/m^{3} \ldotp\]
الدلالة
كثافة المرأة أقل من كثافة السوائل. نتوقع هذا لأنها تطفو.
تطفو العديد من الأجسام أو المواد منخفضة الكثافة في سوائل عالية الكثافة: الزيت على الماء، ومنطاد الهواء الساخن في الغلاف الجوي، وقليلًا من الفلين في النبيذ، وجبل جليدي في الماء المالح، والشمع الساخن في «مصباح الحمم البركانية»، على سبيل المثال لا الحصر. والمثال الأقل وضوحًا هو سلاسل الجبال العائمة على القشرة ذات الكثافة العالية والغطاء تحتها. حتى الأرض التي تبدو صلبة لها خصائص سائلة.
قياس الكثافة
يوضح الشكل أحد الأساليب الأكثر شيوعًا لتحديد الكثافة\(\PageIndex{5}\).
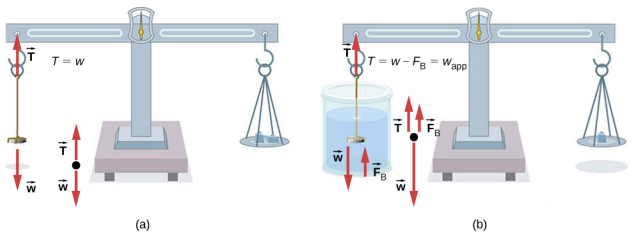
يتم وزن جسم، وهو هنا عملة معدنية، في الهواء ثم يتم وزنه مرة أخرى أثناء غمره في سائل. يمكن حساب كثافة العملة، وهي مؤشر على أصالتها، إذا كانت كثافة السوائل معروفة. يمكننا استخدام نفس الأسلوب لتحديد كثافة السائل إذا كانت كثافة العملة معروفة.
تستند جميع هذه الحسابات إلى مبدأ أرخميدس، الذي ينص على أن قوة الطفو على الجسم تساوي وزن السائل الذي تم إزاحته. وهذا بدوره يعني أن وزن الجسم يبدو أقل عند غمره بالمياه؛ ونطلق على هذا القياس الوزن الظاهري للكائن. يعاني الجسم من فقدان واضح للوزن يساوي وزن السائل الذي تم إزاحته. بدلاً من ذلك، في الموازين التي تقيس الكتلة، يعاني الجسم من فقدان واضح للكتلة يساوي كتلة السائل الذي تم إزاحته. أي أن فقدان الوزن الواضح يساوي وزن السائل الذي تم إزاحته، أو فقدان الكتلة الواضح يساوي كتلة السوائل التي تم إزاحتها.


