14.5: مبدأ باسكال والهيدروليكا
- Page ID
- 200185
- مبدأ الدولة باسكال
- وصف تطبيقات مبدأ باسكال
- اشتقاق العلاقات بين القوى في النظام الهيدروليكي
في عام 1653، نشر الفيلسوف والعالم الفرنسي بليز باسكال أطروحته حول توازن السوائل، والتي ناقش فيها مبادئ السوائل الساكنة. السائل الساكن هو سائل لا يتحرك. عندما لا يتدفق السائل، نقول أن السائل في حالة توازن ثابت. إذا كان السائل عبارة عن ماء، فإننا نقول إنه في حالة توازن هيدروستاتيكي. بالنسبة للسائل في حالة الاتزان الثابت، يجب أن تكون القوة الصافية على أي جزء من السائل صفرًا؛ وإلا سيبدأ السائل في التدفق.
توفر ملاحظات باسكال - منذ إثباتها تجريبيًا - الأساس للهيدروليك، وهي واحدة من أهم التطورات في التكنولوجيا الميكانيكية الحديثة. لاحظ باسكال أن التغيير في الضغط المطبق على السائل المغلق ينتقل بشكل غير منقوص في جميع أنحاء السائل وإلى جدران الحاوية. لهذا السبب، غالبًا ما نعرف عن الضغط أكثر من الكميات الفيزيائية الأخرى في السوائل. علاوة على ذلك، يشير مبدأ باسكال إلى أن الضغط الكلي في السائل هو مجموع الضغوط من مصادر مختلفة. وخير مثال على ذلك هو أن السائل في العمق يعتمد على عمق السائل وضغط الغلاف الجوي.
مبدأ باسكال
ينص مبدأ باسكال (المعروف أيضًا باسم قانون باسكال) على أنه عندما يتم تطبيق تغيير الضغط على سائل مغلق، فإنه ينتقل بشكل غير منقوص إلى جميع أجزاء السائل وإلى جدران الحاوية. في السائل المغلق، نظرًا لأن ذرات السائل حرة في التحرك، فإنها تنقل الضغط إلى جميع أجزاء السائل وإلى جدران الحاوية. أي تغيير في الضغط ينتقل بشكل غير منقوص.
لاحظ أن هذا المبدأ لا ينص على أن الضغط هو نفسه في جميع نقاط السائل - وهذا غير صحيح، لأن الضغط في السائل بالقرب من الأرض يختلف باختلاف الارتفاع. بدلاً من ذلك، ينطبق هذا المبدأ على التغيير في الضغط. لنفترض أنك وضعت بعض الماء في حاوية أسطوانية بارتفاع H ومساحة مقطعية A تحتوي على مكبس متحرك كتلته m (الشكل\(\PageIndex{1}\)). تؤدي إضافة الوزن Mg في الجزء العلوي من المكبس إلى زيادة الضغط في الجزء العلوي بمقدار\(\frac{Mg}{A}\) 2، نظرًا لأن الوزن الإضافي يعمل أيضًا على المنطقة A من الغطاء:
\[\Delta p_{top} = \frac{Mg}{A} \ldotp\]
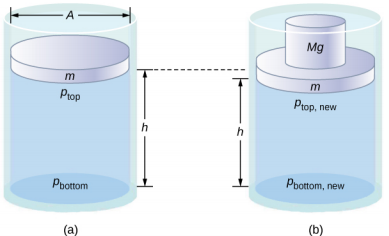
وفقًا لمبدأ باسكال، يتغير الضغط في جميع نقاط الماء بنفس المقدار\(\frac{Mg}{A}\). وبالتالي، يزداد الضغط في الأسفل أيضًا بمقدار\(\frac{Mg}{A}\). الضغط في الجزء السفلي من الحاوية يساوي مجموع الضغط الجوي والضغط الناتج عن السائل والضغط الذي توفره الكتلة. التغيير في الضغط في الجزء السفلي من الحاوية بسبب الكتلة هو
\[\Delta p_{bottom} = \frac{Mg}{A} \ldotp\]
نظرًا لأن تغيرات الضغط هي نفسها في كل مكان في السائل، لم نعد بحاجة إلى رموز فرعية لتعيين تغيير الضغط للجزء العلوي أو السفلي:
\[\Delta p = \Delta p_{top} = \Delta p_{bottom} = \Delta p_{everywhere} \ldotp\]
يعتبر برميل باسكال دليلًا رائعًا على مبدأ باسكال. شاهد محاكاة لتجربة باسكال عام 1646، والتي أظهر فيها تأثيرات تغيير الضغط في السائل.
تطبيقات مبدأ باسكال والأنظمة الهيدروليكية
تستخدم الأنظمة الهيدروليكية لتشغيل فرامل السيارات والرافعات الهيدروليكية والعديد من الأنظمة الميكانيكية الأخرى (الشكل\(\PageIndex{2}\)).
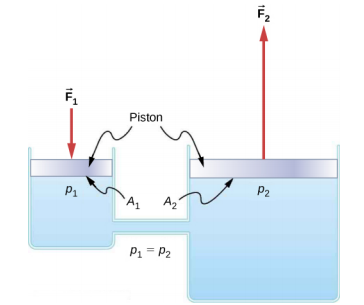
يمكننا استخلاص علاقة بين القوى في هذا النظام الهيدروليكي البسيط من خلال تطبيق مبدأ باسكال. لاحظ أولاً أن المكبسين في النظام لهما نفس الارتفاع، لذلك لا يوجد فرق في الضغط بسبب الاختلاف في العمق. الضغط الناتج عن تأثير F 1 على المنطقة A 1 هو ببساطة
\(p_{1} = \frac{F_{1}}{A_{1}}\)، على النحو المحدد من قبل\(p = \frac{F}{A}\).
وفقًا لمبدأ باسكال، ينتقل هذا الضغط بشكل غير منقوص في جميع أنحاء السائل وإلى جميع جدران الحاوية. وبالتالي، يتم الشعور بالضغط p 2 عند المكبس الآخر الذي يساوي p 1. وهذا هو، ص 1 = ص 2. ومع ذلك، نظرًا لأن p 2 =\(\frac{F_{2}}{A_{2}}\)، نرى ذلك
\[\frac{F_{1}}{A_{1}} = \frac{F_{2}}{A_{2}} \ldotp \label{14.12}\]
تربط هذه المعادلة نسب القوة إلى المساحة في أي نظام هيدروليكي، شريطة أن تكون المكابس في نفس الارتفاع الرأسي وأن يكون الاحتكاك في النظام ضئيلًا.
يمكن للأنظمة الهيدروليكية زيادة أو تقليل القوة المطبقة عليها. لجعل القوة أكبر، يتم تطبيق الضغط على مساحة أكبر. على سبيل المثال، إذا تم تطبيق قوة 100-N على الأسطوانة اليسرى في الشكل 14.16 وكانت مساحة الأسطوانة اليمنى أكبر بخمس مرات، فإن قوة الخرج هي 500 نيوتن. تتشابه الأنظمة الهيدروليكية مع الروافع البسيطة، ولكنها تتميز بإمكانية إرسال الضغط عبر خطوط منحنية بشكل ملتوي إلى عدة الأماكن في وقت واحد.
الرافعة الهيدروليكية هي مثل هذا النظام الهيدروليكي. يتم استخدام الرافعة الهيدروليكية لرفع الأحمال الثقيلة، مثل تلك التي يستخدمها ميكانيكي السيارات لرفع السيارات. يتكون من سائل غير قابل للضغط في أنبوب U مزود بمكبس متحرك على كل جانب. جانب واحد من أنبوب U أضيق من الآخر. يمكن لقوة صغيرة مطبقة على مساحة صغيرة موازنة قوة أكبر بكثير على الجانب الآخر على مساحة أكبر (الشكل\(\PageIndex{3}\)).
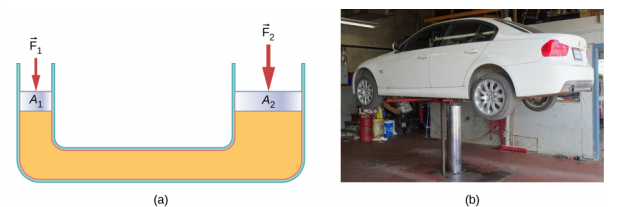
من مبدأ باسكال، يمكن إثبات أن القوة اللازمة لرفع السيارة أقل من وزن السيارة:
\[F_{1} = \frac{A_{1}}{A_{2}} F_{2},\]
حيث F 1 هي القوة المطبقة لرفع السيارة، A 1 هي مساحة المقطع العرضي للمكبس الأصغر، A 2 هي مساحة المقطع العرضي للمكبس الأكبر، و F 2 هي وزن السيارة.
ضع في اعتبارك النظام الهيدروليكي للسيارات الموضح في الشكل\(\PageIndex{4}\). لنفترض أنه تم تطبيق قوة مقدارها 100 نيوتن على دواسة الفرامل، التي تعمل على أسطوانة الدواسة (تعمل كأسطوانة «رئيسية») من خلال رافعة. تُؤثِّر قوة مقدارها 500 نيوتن على أسطوانة الدواسة. يتم نقل الضغط الناتج في أسطوانة الدواسة إلى أسطوانات العجلات الأربع. يبلغ قطر أسطوانة الدواسة 0.500 سم وقطر كل أسطوانة 2.50 سم. احسب مقدار القوة F 2 الناتجة في كل أسطوانة من أسطوانات العجلات.
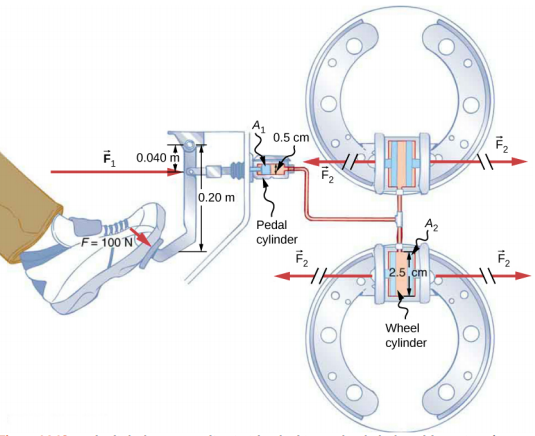
إستراتيجية
يتم منحنا القوة F 1 المطبقة على أسطوانة الدواسة. يمكن حساب مناطق المقطع العرضي A 1 و A 2 من أقطارها المحددة. ثم يمكننا استخدام العلاقة التالية للعثور على القوة F 2:
\[\frac{F_{1}}{A_{1}} = \frac{F_{2}}{A_{2}} \ldotp\]
تعامل مع هذا جبريًا للحصول على F 2 على جانب واحد واستبدال القيم المعروفة.
الحل
يتم تطبيق مبدأ Pascal على الأنظمة الهيدروليكية من خلال\(\frac{F_{1}}{A_{1}} = \frac{F_{2}}{A_{2}}\):
\[\begin{split} F_{2} & = \frac{A_{2}}{A_{1}} F_{1} = \frac{\pi r_{2}^{2}}{\pi r_{1}^{2}} F_{1} \\ & = \frac{(1.25\; cm)^{2}}{(0.250\; cm)^{2}} \times 500\; N = 1.25 \times 10^{4}\; N \ldotp \end{split}\]
الدلالة
هذه القيمة هي القوة التي تؤثِّر بها كل أسطوانة من الأسطوانات ذات العجلات الأربع. لاحظ أنه يمكننا إضافة العديد من أسطوانات العجلات كما يحلو لنا. إذا كان قطر كل منها 2.50 سم، فسوف يستهلك كل منها 1.25 × 10 4 نيوتن. يمكن للنظام الهيدروليكي البسيط، كمثال لآلة بسيطة، زيادة القوة ولكن لا يمكنه القيام بعمل أكثر مما يتم القيام به عليه. العمل هو القوة مضروبًا في المسافة، وتحرك أسطوانة العجلة عبر مسافة أصغر من أسطوانة الدواسة. علاوة على ذلك، كلما تمت إضافة المزيد من العجلات، كلما قلت المسافة التي تتحرك فيها كل واحدة. تحتوي العديد من الأنظمة الهيدروليكية - مثل الفرامل الكهربائية وتلك الموجودة في الجرافات - على مضخة آلية تقوم بالفعل بمعظم العمل في النظام.
هل ستستمر الصحافة الهيدروليكية في العمل بشكل صحيح إذا تم استخدام الغاز بدلاً من السائل؟


