14.3: السوائل والكثافة والضغط (الجزء 2)

Last updated
Save as PDF

Page ID: 200159

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

تباين الضغط مع العمق في سائل ذي كثافة ثابتة

يتم تحديد الضغط لجميع حالات المادة، ولكنه مهم بشكل خاص عند مناقشة السوائل. من الخصائص المهمة للسوائل عدم وجود مقاومة كبيرة لمكون القوة المطبقة بالتوازي مع سطح السائل. تتدفق جزيئات السائل ببساطة لاستيعاب القوة الأفقية. تعمل القوة التي تُؤثِّر بشكل عمودي على السطح على ضغط السائل أو توسيعه. إذا حاولت ضغط السائل، ستجد أن قوة التفاعل تتطور عند كل نقطة داخل السائل في الاتجاه الخارجي، لتوازن القوة المطبقة على الجزيئات عند الحد.

ضع في اعتبارك سائلًا ذا كثافة ثابتة كما هو موضح في الشكل$\PageIndex{1}$. يرجع الضغط في الجزء السفلي من الحاوية إلى ضغط الغلاف الجوي (p ₀) بالإضافة إلى الضغط الناتج عن وزن السائل. الضغط الناتج عن السائل يساوي وزن السائل مقسومًا على المنطقة. وزن السائل يساوي كتلته مضروبًا في التسارع الناتج عن الجاذبية.

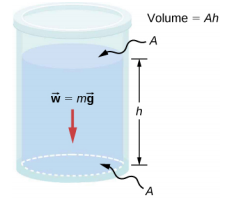
الشكل A عبارة عن رسم لحاوية. يحتوي الجزء السفلي من الحاوية على مساحة A. الحاوية مملوءة بالسائل حتى الارتفاع h. النص الموجود على يمين الحاوية مكتوب عليه «الحجم يساوي A مضروبًا في h». — الشكل$\PageIndex{1}$: الجزء السفلي من هذه الحاوية يدعم الوزن الكامل للسائل الموجود فيها. لا يمكن للجوانب الرأسية أن تمارس قوة تصاعدية على السائل (نظرًا لأنه لا يمكنه تحمل قوة القص)، لذلك يجب أن يدعمه الجزء السفلي كله.

نظرًا لأن الكثافة ثابتة، يمكن حساب الوزن باستخدام الكثافة:

\[w = mg = \rho Vg = \rho Ahg \ldotp\]

وبالتالي فإن الضغط في الجزء السفلي من الحاوية يساوي الضغط الجوي المضاف إلى وزن السائل مقسومًا على المنطقة:

\[p = p_{0} + \frac{\rho Ahg}{A} = p_{0} + \rho hg \ldotp\]

هذه المعادلة جيدة فقط للضغط على عمق مائع ذي كثافة ثابتة

الضغط على العمق لمائع ذي كثافة ثابتة

الضغط عند عمق سائل ذي كثافة ثابتة يساوي ضغط الغلاف الجوي بالإضافة إلى الضغط الناتج عن وزن السائل، أو

\[p = p_{0} + \rho hg, \label{14.4}\]

حيث p هو الضغط عند عمق معين، p ₀ هو ضغط الغلاف الجوي،$\rho$ هو كثافة السائل، g هو التسارع بسبب الجاذبية، و h هو العمق.

صورة لسد أقيم على نهر. — الشكل$\PageIndex{2}$: أدى سد الخوانق الثلاثة، الذي أقيم على نهر اليانغتسي في وسط الصين في عام 2008، إلى إنشاء خزان ضخم أدى إلى نزوح أكثر من مليون شخص. (تصوير: «لو جراند بورتاج» /فليكر)

مثال 14.1: ما القوة التي يجب أن يتحملها السد؟

ضع في اعتبارك الضغط والقوة المؤثرة على السد الذي يحتفظ بخزان الماء (الشكل$\PageIndex{2}$). لنفترض أن عرض السد يبلغ 500 متر وعمق المياه 80 مترًا عند السد، كما هو موضح أدناه. (أ) ما هو متوسط الضغط على السد بسبب الماء؟ (ب) احسب القوة المؤثرة على السد.

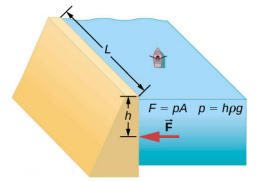
الشكل عبارة عن رسم تخطيطي لسد بطول L وارتفاع h تم نصبه على النهر. هناك زورق صغير في النهر مع راكب واحد. يتضمن هذا الرسم التوضيحي الصيغ F تساوي p مضروبًا في A، وp تساوي h مضروبًا في p مضروبًا في g.

متوسط الضغط p بسبب وزن الماء هو الضغط عند متوسط عمق h البالغ 40.0 مترًا، حيث يزداد الضغط خطيًا مع العمق. القوة المؤثرة على السد بواسطة الماء هي متوسط الضغط مضروبًا في منطقة التلامس، F = pA.

الحل

متوسط الضغط الناتج عن وزن السائل هو $p = h\ rho g\ ldotp\ label {14.5} $عند إدخال كثافة الماء من الجدول 14.1 ومع الأخذ في الاعتبار أن متوسط العمق هو 40.0 م، نحصل على $$\ begin {split} p & = (40.0\; m) (10^ {3}\; كجم/م^ {3}) (9.80\; م/s^ {2})\\ & = 3.92\ مرات 10^ {5}\؛ N/M^ {2} = 392\؛ pa\ ldotp\ end {الانقسام} $$
لقد وجدنا بالفعل قيمة p. مساحة السد هي $A = (80.0\; m)\ مرات (500\; م) = 4.00\ مرات 10^ {4}\؛ m^ {2}\ ldotp$$بحيث $$\ يبدأ {الانقسام} F & = (3.92\ مرات 10^ {5}\؛ N/m^ {2}) (4.00\ مرات 10^ 4)}\؛ m^ {2})\\ & = 1.57\ مرات 10^ {10}\؛ M\ ldotp\ end {الانقسام} $$

الدلالة

على الرغم من أن هذه القوة تبدو كبيرة، إلا أنها صغيرة مقارنة بوزن 1.96 × 10 ¹³ نيوتن للمياه في الخزان. في الواقع، إنها تمثل 0.0800٪ فقط من الوزن.

التمرين 14.1

إذا كان الخزان في المثال$\PageIndex{1}$ يغطي ضعف المساحة، ولكن تم الاحتفاظ به بنفس العمق، فهل يلزم إعادة تصميم السد؟

الضغط في سائل ثابت في مجال جاذبية منتظم

السائل الساكن هو سائل لا يتحرك. في أي نقطة داخل السائل الساكن، يجب أن يكون الضغط على جميع الجوانب متساويًا - وإلا فإن السائل عند هذه النقطة سوف يتفاعل مع القوة الصافية ويتسارع.

يعتمد الضغط عند أي نقطة في السائل الساكن فقط على العمق عند تلك النقطة. كما تمت مناقشته، يختلف الضغط في السائل بالقرب من الأرض باختلاف العمق بسبب وزن السائل فوق مستوى معين. في الأمثلة أعلاه، افترضنا أن الكثافة ثابتة وأن متوسط كثافة السائل يمثل تمثيلًا جيدًا للكثافة. هذا تقدير تقريبي معقول للسوائل مثل الماء، حيث تكون هناك حاجة لقوى كبيرة لضغط السائل أو تغيير الحجم. في حمام السباحة، على سبيل المثال، تكون الكثافة ثابتة تقريبًا، والماء الموجود في الأسفل يتم ضغطه قليلًا جدًا بسبب وزن الماء الموجود في الأعلى. ومع ذلك، فإن السفر في الغلاف الجوي هو وضع مختلف تمامًا. تبدأ كثافة الهواء بالتغير بشكل كبير على مسافة قصيرة فوق سطح الأرض.

لاستخلاص صيغة لتغير الضغط مع العمق في خزان يحتوي على سائل الكثافة$\rho$ على سطح الأرض، يجب أن نبدأ بافتراض أن كثافة السائل ليست ثابتة. يتعرض السائل الموجود في مستويات أعمق لقوة أكبر من السائل الأقرب إلى السطح بسبب وزن السائل الموجود فوقه. لذلك، يختلف الضغط المحسوب على عمق معين عن الضغط المحسوب باستخدام كثافة ثابتة.

تخيل عنصرًا رقيقًا من السائل على عمق h، كما هو موضح في الشكل$\PageIndex{3}$. دع العنصر يحتوي على مساحة المقطع العرضي A والارتفاع$\Delta$ y، وتعزى القوى المؤثرة على العنصر إلى الضغوط p (y) أعلاه و p (y +$\Delta$ y) تحته. يظهر وزن العنصر نفسه أيضًا في مخطط الجسم الحر.

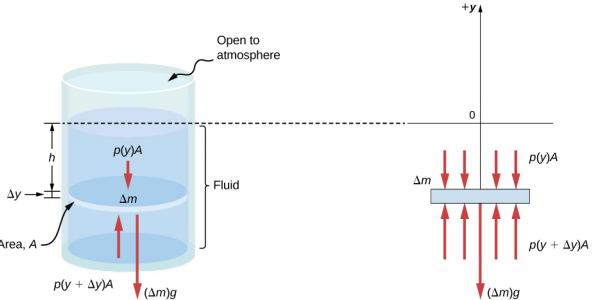
الشكل A عبارة عن رسم تخطيطي لأسطوانة مليئة بالسوائل ومفتوحة للغلاف الجوي في الأعلى. وُضع في السائل قرص كتلته دلتا م ومساحة سطحه A مطابقة لمساحة سطح الأسطوانة وارتفاعه Delta y. يوجد مائع بارتفاع h فوق القرص. الشكل B عبارة عن رسم تخطيطي لقوة Delta m x g التي يعبر عنها القرص، و p (y) x A التي يطبقها السائل الموجود فوق القرص، و p (y + Delta y) x A التي يطبقها السائل الموجود أسفل القرص. — الشكل$\PageIndex{3}$: القوى المؤثرة على عنصر الكتلة داخل السائل. يظهر وزن العنصر نفسه في مخطط الجسم الحر.

نظرًا لأن عنصر السائل بين y و y +$\Delta$ y لا يتسارع، فإن القوى متوازنة. باستخدام محور y الكارتيزي الموجه لأعلى، نجد المعادلة التالية للمكون y:

\[p(y + \Delta y)A - p(y)A - g \Delta m = 0(\Delta y < 0) \ldotp \label{14.6}\]

لاحظ أنه إذا كان العنصر يحتوي على مكون التسارع y غير الصفري، فلن يكون الجانب الأيمن صفرًا ولكن بدلاً من ذلك سيكون الكتلة مضروبًا في التسارع y. يمكن كتابة كتلة العنصر من حيث كثافة السائل وحجم العناصر:

\[\Delta m = |\rho A \Delta y| = - \rho A \Delta y \quad (\Delta y < 0) \ldotp\]

بوضع هذا التعبير عن$\Delta$ m في المعادلة\ ref {14.6} ثم تقسيم كلا الجانبين على A$\Delta$ y، نجد

\[\frac{p(y + \Delta y) - p(y)}{\Delta y} = - \rho g \ldotp \label{14.7}\]

عند أخذ حد العنصر الرقيق للغاية$\Delta$ y → 0، نحصل على المعادلة التفاضلية التالية، والتي تعطي تباين الضغط في السائل:

\[\frac{dp}{dy} = - \rho g \ldotp \label{14.8}\]

تخبرنا هذه المعادلة أن معدل تغير الضغط في السائل يتناسب مع كثافة السائل. يعتمد حل هذه المعادلة على ما إذا كانت الكثافة$\rho$ ثابتة أو تتغير مع العمق؛ أي الدالة$\rho$ (y).

إذا لم يكن نطاق العمق الذي يتم تحليله كبيرًا جدًا، فيمكننا افتراض أن الكثافة ثابتة. ولكن إذا كان نطاق العمق كبيرًا بما يكفي لتباين الكثافة بشكل ملحوظ، كما هو الحال في الغلاف الجوي، فهناك تغير كبير في الكثافة مع العمق. في هذه الحالة، لا يمكننا استخدام تقريب الكثافة الثابتة.

الضغط في سائل ذو كثافة ثابتة

دعونا نستخدم المعادلة\ ref {14.9} لإيجاد صيغة للضغط على عمق h من السطح في خزان سائل مثل الماء، حيث يمكن اعتبار كثافة السائل ثابتة.

رسم تخطيطي للدورق المملوء بالسائل إلى الارتفاع h. يُظهر السائل ضغطًا P0 يساوي الصفر عند السطح والضغط P في الجزء السفلي من الكأس.

نحتاج إلى دمج المعادلة\ ref {14.9} من y = 0، حيث يكون الضغط هو الضغط الجوي (p ₀)، إلى y = −h، الإحداثي y للعمق:

\[\begin{split} \int_{p_{0}}^{p} dp & = - \int_{0}^{-h} \rho gdy \\ p - p_{0} & = \rho gh \\ p & = p_{0} + \rho gh \ldotp \end{split} \label{14.9}\]

وبالتالي، فإن الضغط عند عمق السائل على سطح الأرض يساوي الضغط الجوي زائد$\rho$ gh إذا كانت كثافة السائل ثابتة على الارتفاع، كما وجدنا سابقًا.

لاحظ أن الضغط في السائل يعتمد فقط على العمق من السطح وليس على شكل الحاوية. وبالتالي، في الحاوية التي يمكن أن يتحرك فيها السائل بحرية في أجزاء مختلفة، يظل السائل عند نفس المستوى في كل جزء، بغض النظر عن الشكل، كما هو موضح في الشكل$\PageIndex{4}$.

صورة لبعض الحاويات الزجاجية ذات الأشكال المختلفة المتصلة بأنبوب زجاجي في الأسفل ومليئة بسائل أحمر. يكون السائل على نفس الارتفاع في الحاويات الزجاجية المختلفة. — الشكل$\PageIndex{4}$: إذا كان السائل يمكن أن يتدفق بحرية بين أجزاء الحاوية، فإنه يرتفع إلى نفس الارتفاع في كل جزء. في الحاوية المصورة، يكون الضغط في أسفل كل عمود هو نفسه؛ وإذا لم يكن هو نفسه، فسوف يتدفق السائل حتى تصبح الضغوط متساوية.

اختلاف الضغط الجوي مع الارتفاع

يعتبر التغيير في الضغط الجوي مع الارتفاع ذا أهمية خاصة. بافتراض أن درجة حرارة الهواء ثابتة، وأن قانون الغاز المثالي للديناميكا الحرارية يصف الغلاف الجوي بتقريب جيد، يمكننا أن نجد تباين الضغط الجوي مع الارتفاع، عندما تكون درجة الحرارة ثابتة. (نناقش قانون الغاز المثالي في فصل لاحق، لكننا نفترض أن لديك بعض الإلمام به من المدرسة الثانوية والكيمياء.) لنفترض أن p (y) هو الضغط الجوي عند الارتفاع y، وترتبط الكثافة$\rho$ عند y، ودرجة الحرارة T في مقياس كلفن (K)، والكتلة m لجزيء الهواء بالضغط المطلق بموجب قانون الغاز المثالي، في الشكل

\[p = \rho \frac{k_{B} T}{m}\; (atmosphere), \label{14.10}\]

حيث k _B هو ثابت بولتزمان، الذي تبلغ قيمته 1.38 × 10 ⁻²³ J/K.

ربما واجهت قانون الغاز المثالي في النموذج pV = nRT، حيث n هو عدد المولات و R هو ثابت الغاز. هنا، تمت كتابة نفس القانون في شكل مختلف، باستخدام الكثافة$\rho$ بدلاً من المجلد V. لذلك، إذا تغير الضغط p مع الارتفاع، فإن الكثافة تتغير أيضًا$\rho$. باستخدام الكثافة من قانون الغاز المثالي، يُعطى معدل تغير الضغط مع الارتفاع على النحو التالي:

\[\frac{dp}{dy} = -p \left(\dfrac{mg}{k_{B} T}\right),\]

حيث تم جمع كميات ثابتة داخل الأقواس. باستبدال هذه الثوابت برمز واحد$\alpha$، تبدو المعادلة أبسط بكثير:

\[\begin{split} \frac{dp}{dy} & = - \alpha p \\ \frac{dp}{p} & = - \alpha dy \\ \int_{p_{0}}^{p(y)} \frac{dp}{p} & = \int_{0}^{y} - \alpha dy \\ [\ln (p)]_{p_{0}}^{p(y)} & = [- \alpha y]_{0}^{y} \\ \ln (p) - \ln (p_{0}) & = - \alpha y \\ \ln \left(\dfrac{p}{p_{0}}\right) & = - \alpha y \end{split}\]

هذا يعطي الحل

\[p(y) = p_{0} e^{- \alpha y} \ldotp\]

وبالتالي، ينخفض الضغط الجوي بشكل كبير مع الارتفاع، حيث يتم توجيه المحور y لأعلى من الأرض و y له قيم موجبة في الغلاف الجوي فوق مستوى سطح البحر. ينخفض الضغط بعامل$\frac{1}{e}$ عندما يكون الارتفاع$\frac{1}{\alpha}$، مما يعطينا تفسيرًا ماديًا لـ$\alpha$: الثابت$\frac{1}{\alpha}$ هو مقياس الطول الذي يميز كيفية اختلاف الضغط مع الارتفاع وغالبًا ما يشار إليه باسم ارتفاع مقياس الضغط.

يمكننا الحصول على قيمة تقريبية$\alpha$ باستخدام كتلة جزيء النيتروجين كبديل لجزيء الهواء. عند درجة حرارة 27 درجة مئوية، أو 300 كلفن، نجد

\[\alpha = - \frac{mg}{k_{B} T} = \frac{(4.8 \times 10^{-26}\; kg) \times (9.81\; m/s^{2})}{(1.38 \times 10^{-23}\; J/K) \times (300\; K)} = \frac{1}{8800\; m} \ldotp\]

لذلك، لكل 8800 متر، ينخفض ضغط الهواء بعامل 1/e، أو ما يقرب من ثلث قيمته. هذا يعطينا فقط تقديرًا تقريبيًا للوضع الفعلي، حيث افترضنا كلاً من درجة حرارة ثابتة و g ثابتة على هذه المسافات الكبيرة من الأرض، وكلاهما غير صحيح في الواقع.

اتجاه الضغط في السائل

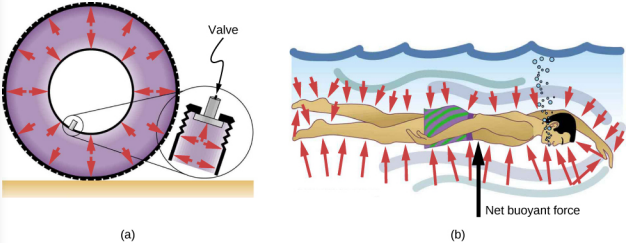
لا يوجد اتجاه لضغط السائل، كونه كمية قياسية، في حين أن القوى الناتجة عن الضغط لها اتجاهات محددة جيدًا: يتم ممارستها دائمًا بشكل عمودي على أي سطح. والسبب هو أن السوائل لا يمكنها تحمل أو ممارسة قوى القص. وهكذا، في سائل ثابت محاط بخزان، تُمارس القوة المؤثرة على جدران الخزان بشكل عمودي على السطح الداخلي. وبالمثل، يتم ممارسة الضغط بشكل عمودي على أسطح أي جسم داخل السائل. $\PageIndex{5}$يوضح الشكل الضغط الذي يمارسه الهواء على جدران الإطار والماء على جسم السباح.

الشكل A هو رسم تخطيطي لإطار مملوء بالهواء. يمارس الضغط داخل هذا الإطار قوى عمودية على جميع الأسطح التي يلامسها، بما في ذلك الصمام. الشكل B هو رسم تخطيطي للسباح تحت الماء. يتم ممارسة الضغط بشكل عمودي على جميع جوانب هذا السباح مع قوة طفو صافية أكبر تحت السباح. — الشكل$\PageIndex{5}$: (أ) الضغط داخل هذا الإطار يمارس قوى عمودية على جميع الأسطح التي يلامسها. تمثل الأسهم اتجاهات ومقادير القوى المؤثرة في نقاط مختلفة. (ب) يتم الضغط بشكل عمودي على جميع جوانب هذا السباح، لأن الماء سيتدفق إلى الفضاء الذي يشغله إذا لم يكن هناك. تمثل الأسهم اتجاهات ومقاييس القوى المؤثرة في نقاط مختلفة على السباح. لاحظ أن القوى أكبر من الأسفل، بسبب العمق الأكبر، مما يعطي قوة صاعدة أو طافية صافية. القوة الرأسية الصافية على السباح تساوي مجموع قوة الطفو ووزن السباح.