10.6: حساب لحظات القصور الذاتي
- Page ID
- 200000
- احسب لحظة القصور الذاتي للأجسام الصلبة ذات الشكل الموحد
- طبّق نظرية المحور الموازي لإيجاد لحظة القصور الذاتي حول أي محور موازي لمحور معروف بالفعل
- احسب لحظة القصور الذاتي للأجسام المركبة
في القسم الفرعي السابق، حددنا لحظة القصور الذاتي ولكننا لم نوضح كيفية حسابها. في هذا القسم الفرعي، نعرض كيفية حساب لحظة القصور الذاتي للعديد من الأنواع القياسية من الكائنات، وكذلك كيفية استخدام لحظات القصور الذاتي المعروفة للعثور على لحظة القصور الذاتي لمحور متحول أو لكائن مركب. هذا القسم مفيد جدًا لمعرفة كيفية تطبيق معادلة عامة على الأشياء المعقدة (مهارة مهمة لدورات الفيزياء والهندسة الأكثر تقدمًا).
لحظة القصور الذاتي
لقد حددنا لحظة القصور الذاتي I للكائن المراد
\[I = \sum_{i} m_i r_i^2 \]
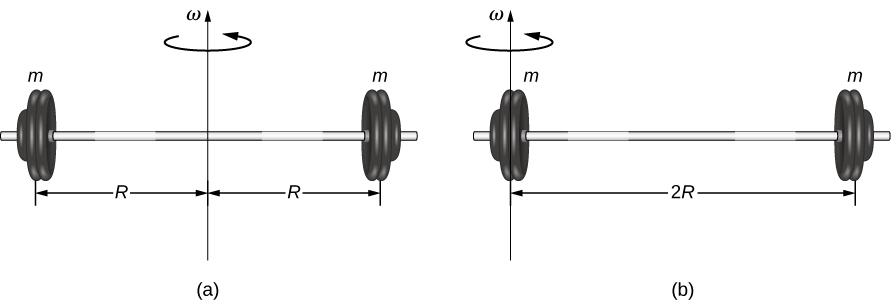
لكل كتل النقاط التي يتكون منها الكائن. نظرًا\(r\) لأن المسافة إلى محور الدوران من كل قطعة من الكتلة التي تشكل الكائن، تعتمد لحظة القصور الذاتي لأي كائن على المحور المختار. لنرى هذا، لنأخذ مثالًا بسيطًا لكتلتين في نهاية قضيب عديم الكتلة (كتلة صغيرة جدًا) (الشكل\(\PageIndex{1}\)) ونحسب لحظة القصور الذاتي حول محورين مختلفين. في هذه الحالة، يكون الجمع فوق الكتل بسيطًا لأن الكتلتين في نهاية الحديد يمكن تقريبهما في صورة كتل نقطية، وبالتالي فإن المجموع يتكون من حدين فقط.
في حالة المحور الموجود في مركز الحديد، تكون كل كتلة من الكتلتين m على بعد\(R\) مسافة من المحور، مما يعطي لحظة من القصور الذاتي
\[I_{1} = mR^{2} + mR^{2} = 2mR^{2} \ldotp\]
في حالة المحور الموجود في نهاية الحديد - الذي يمر عبر إحدى الكتل - تكون لحظة القصور الذاتي
\[I_{2} = m(0)^{2} + m(2R)^{2} = 4mR^{2} \ldotp\]
من هذه النتيجة، يمكننا أن نستنتج أنه من الصعب تدوير الحديد حول نهايته بمقدار الضعف مقارنة بمركزه.
في هذا المثال، كانت لدينا كتلتان من نقطتين وكان من السهل حساب المجموع. ومع ذلك، للتعامل مع الأشياء التي لا تشبه النقاط، نحتاج إلى التفكير بعناية في كل مصطلح من المصطلحات في المعادلة. تطلب المعادلة أن نجمع على كل «قطعة كتلة» مسافة معينة من محور الدوران. ولكن ماذا تعني بالضبط كل «قطعة من الكتلة»؟ تذكر أنه في اشتقاقنا لهذه المعادلة، كان لكل قطعة كتلة نفس مقدار السرعة، مما يعني أن القطعة بأكملها يجب أن تكون لها مسافة واحدة r إلى محور الدوران. ومع ذلك، فإن هذا غير ممكن ما لم نأخذ قطعة صغيرة للغاية من الكتلة dm، كما هو موضح في الشكل\(\PageIndex{2}\).
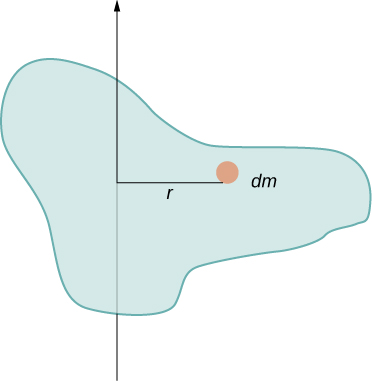
تشير الحاجة إلى استخدام قطعة صغيرة للغاية من الكتلة dm إلى أنه يمكننا كتابة لحظة القصور الذاتي من خلال تقييم التكامل فوق الكتل متناهية الصغر بدلاً من إجراء مجموع منفصل على كتل محدودة:
\[I = \sum_{i} m_{i} r_{i}^{2}\]
يصبح
\[I = \int r^{2} dm \ldotp \label{10.19}\]
هذا، في الواقع، هو الشكل الذي نحتاجه لتعميم المعادلة للأشكال المعقدة. من الأفضل وضع أمثلة محددة بالتفصيل للتعرف على كيفية حساب لحظة القصور الذاتي لأشكال معينة. هذا هو محور معظم بقية هذا القسم.
قضيب رقيق موحد مع محور يمر عبر المركز
ضع في اعتبارك قضيبًا رقيقًا موحدًا (الكثافة والشكل) كتلته M وطوله L كما هو موضح في الشكل\(\PageIndex{3}\). نريد قضيبًا رقيقًا حتى نتمكن من افتراض أن مساحة المقطع العرضي للقضيب صغيرة ويمكن اعتبار القضيب كسلسلة من الكتل على طول خط مستقيم أحادي البعد. في هذا المثال، يكون محور الدوران عموديًا على القضيب ويمر عبر نقطة الوسط من أجل البساطة. مهمتنا هي حساب لحظة القصور الذاتي حول هذا المحور. نقوم بتوجيه المحاور بحيث يكون المحور z هو محور الدوران ويمر المحور السيني بطول القضيب، كما هو موضح في الشكل. يعد هذا اختيارًا مناسبًا لأنه يمكننا بعد ذلك الاندماج على طول المحور x.
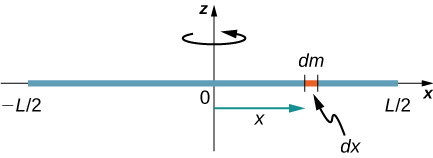
نحدد dm على أنه عنصر صغير من الكتلة التي تشكل القضيب. تعتبر لحظة القصور الذاتي جزءًا لا يتجزأ من التوزيع الشامل. ومع ذلك، نحن نعرف كيفية الاندماج عبر الفضاء، وليس عبر الكتلة. لذلك نحن بحاجة إلى إيجاد طريقة لربط الكتلة بالمتغيرات المكانية. نقوم بذلك باستخدام كثافة الكتلة الخطية\(\lambda\) للكائن، وهي الكتلة لكل وحدة طول. نظرًا لأن الكثافة الكتلية لهذا الكائن موحدة، يمكننا الكتابة
\[\lambda = \frac{m}{l}\; or\; m = \lambda l \ldotp\]
إذا أخذنا الفرق بين طرفي هذه المعادلة، نجد
\[dm = d(\lambda l) = \lambda (dl)\]
\(\lambda\)لأنه ثابت. لقد اخترنا توجيه القضيب على طول المحور السيني من أجل الراحة - وهنا يصبح هذا الاختيار مفيدًا جدًا. لاحظ أن قطعة من القضيب dl تقع بالكامل على طول المحور x ويبلغ طولها dx؛ في الواقع، dl = dx في هذه الحالة. لذلك يمكننا كتابة dm =\(\lambda\) (dx)، مما يعطينا متغير تكامل نعرف كيفية التعامل معه. يتم تحديد مسافة كل قطعة من الكتلة dm من المحور بواسطة المتغير x، كما هو موضح في الشكل. بتجميع كل هذا معًا، نحصل عليه
\[I = \int r^{2} dm = \int x^{2} dm = \int x^{2} \lambda dx \ldotp\]
الخطوة الأخيرة هي توخي الحذر بشأن حدود التكامل لدينا. يمتد القضيب من x =\(− \frac{L}{2}\) إلى x =\(\frac{L}{2}\)، نظرًا لأن المحور يقع في منتصف القضيب عند x = 0. هذا يعطينا
\[\begin{split} I & = \int_{- \frac{L}{2}}^{\frac{L}{2}} x^{2} \lambda dx = \lambda \frac{x^{3}}{3} \Bigg|_{- \frac{L}{2}}^{\frac{L}{2}} \\ & = \lambda \left(\dfrac{1}{3}\right) \Bigg[ \left(\dfrac{L}{2}\right)^{3} - \left(- \dfrac{L}{2}\right)^{3} \Bigg] = \lambda \left(\dfrac{1}{3}\right) \left(\dfrac{L^{3}}{8}\right) (2) = \left(\dfrac{M}{L}\right) \left(\dfrac{1}{3}\right) \left(\dfrac{L^{3}}{8}\right) (2) \\ & = \frac{1}{12} ML^{2} \ldotp \end{split}\]
بعد ذلك، نحسب لحظة القصور الذاتي لنفس القضيب الرقيق الموحد ولكن باختيار محور مختلف حتى نتمكن من مقارنة النتائج. نتوقع أن تكون لحظة القصور الذاتي أصغر حول محور يمر بمركز الكتلة مقارنة بمحور نقطة النهاية، تمامًا كما كان الحال بالنسبة لمثال الحديد في بداية هذا القسم. يحدث هذا بسبب توزيع المزيد من الكتلة بعيدًا عن محور الدوران.
قضيب رقيق موحد بمحور في نهايته
الآن فكر في نفس القضيب الرقيق الموحد من الكتلة\(M\) والطول\(L\)، ولكن هذه المرة نقوم بتحريك محور الدوران إلى نهاية القضيب. نتمنى أن نجد لحظة القصور الذاتي حول هذا المحور الجديد (الشكل\(\PageIndex{4}\)).
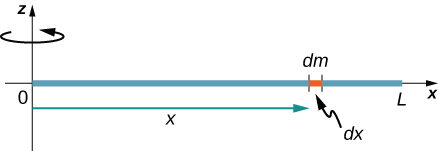
\(dm\)يتم تعريف الكمية مرة أخرى على أنها عنصر صغير من الكتلة يتكون من القضيب. تمامًا كما كان من قبل، نحصل على
\[I = \int r^{2} dm = \int x^{2} dm = \int x^{2} \lambda dx \ldotp\]
ومع ذلك، لدينا هذه المرة حدود مختلفة للتكامل. يمتد القضيب من\(x = 0\) إلى\(x = L\)، لأن المحور يقع في نهاية القضيب عند\(x = 0\). لذلك نجد
\[\begin{align} I & = \int_{0}^{L} x^{2} \lambda\, dx \\[4pt] &= \lambda \frac{x^{3}}{3} \Bigg|_{0}^{L} \\[4pt] &=\lambda \left(\dfrac{1}{3}\right) \Big[(L)^{3} - (0)^{3} \Big] \\[4pt] & = \lambda \left(\dfrac{1}{3}\right) L^{3} = \left(\dfrac{M}{L}\right) \left(\dfrac{1}{3}\right) L^{3} \\[4pt] &= \frac{1}{3} ML^{2} \ldotp \label{ThinRod} \end{align} \]
لاحظ أن القصور الذاتي الدوراني للقضيب حول نقطة نهايته أكبر من القصور الذاتي الدوراني حول مركزه (بما يتفق مع مثال الحديد) بعامل أربعة.
نظرية المحور المتوازي
إن التشابه بين عملية العثور على لحظة القصور الذاتي للقضيب حول محور يمر عبر وسطه وحول محور من خلال نهايته أمر مذهل، ويشير إلى أنه قد تكون هناك طريقة أبسط لتحديد لحظة القصور الذاتي لقضيب حول أي محور مواز للمحور عبر مركز حجم. مثل هذا المحور يسمى المحور الموازي. هناك نظرية لهذا، تسمى نظرية المحور الموازي، التي نذكرها هنا ولكننا لا نستمدها في هذا النص.
اسمحوا m أن تكون كتلة كائن ولتكن d هي المسافة من محور عبر مركز كتلة الكائن إلى محور جديد. ثم لدينا
\[I_{\text{parallel-axis}} = I_{\text{center of mass}} + md^{2} \ldotp \label{10.20}\]
دعنا نطبق هذا على القضيب الرقيق الموحد مع مثال المحور الذي تم حله أعلاه:
\[I_{parallel-axis} = I_{center\; of\; mass} + md^{2} = \frac{1}{12} mL^{2} + m \left(\dfrac{L}{2}\right)^{2} = \left(\dfrac{1}{12} + \dfrac{1}{4}\right) mL^{2} = \frac{1}{3} mL^{2} \ldotp\]
تتوافق هذه النتيجة مع حسابنا الأطول (المعادلة\ ref {ThinRod}). المعادلة\ ref {10.20} هي معادلة مفيدة نطبقها في بعض الأمثلة والمشاكل.
ما عزم القصور الذاتي لأسطوانة نصف قطرها\(R\) وكتلتها\(m\) حول محور يمر بنقطة على السطح، كما هو موضح أدناه؟
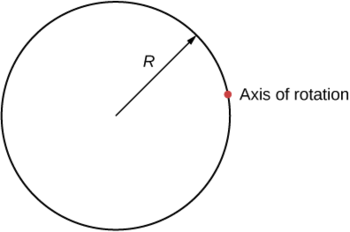
- إجابة
-
\[I_{parallel-axis} = I_{center\; of\; mass} + md^{2} = mR^{2} + mR^{2} = 2mR^{2} \nonumber \]
قرص رقيق منتظم حول محور يمر عبر المركز
يعد التكامل للعثور على لحظة القصور الذاتي لجسم ثنائي الأبعاد أمرًا صعبًا بعض الشيء، ولكن يتم عمل شكل واحد بشكل شائع في هذا المستوى من الدراسة - قرص رقيق موحد حول محور يمر عبر مركزه (الشكل\(\PageIndex{5}\)).
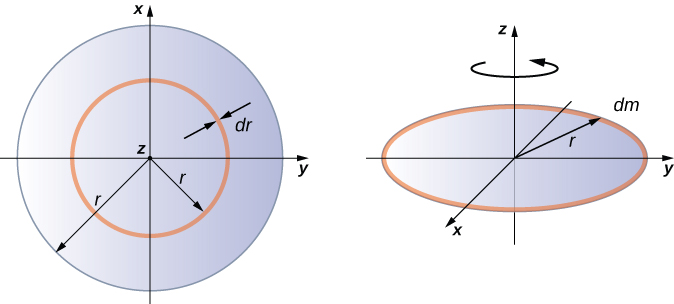
نظرًا لأن القرص رقيق، يمكننا أخذ الكتلة كما تم توزيعها بالكامل في المستوى xy. نبدأ مرة أخرى بالعلاقة بين كثافة الكتلة السطحية، وهي الكتلة لكل وحدة مساحة سطح. نظرًا لتوحيدها،\(\sigma\) تكون كثافة الكتلة السطحية ثابتة:
\[\sigma = \frac{m}{A}\]أو نحو\[\sigma A = m\] ذلك\[dm = \sigma (dA)\]
الآن نستخدم التبسيط للمنطقة. يمكن اعتبار المنطقة مكونة من سلسلة من الحلقات الرقيقة، حيث تكون كل حلقة عبارة عن زيادة كتلة نصف قطرها نصف قطر\(r\) متساوي البعد عن المحور، كما هو موضح في الجزء (ب) من الشكل. لذلك\(dA\) يتم تحديد المساحة متناهية الصغر لكل حلقة من خلال طول كل حلقة (\(2 \pi r\)) مضروبًا في العرض اللانهائي لكل حلقة\(dr\):
\[A = \pi r^{2},\; dA = d(\pi r^{2}) = \pi dr^{2} = 2 \pi rdr \ldotp\]
ثم تتكون المساحة الكاملة للقرص من إضافة جميع الحلقات الرقيقة بنطاق نصف قطر من\(0\) إلى\(R\). يصبح نطاق النطاق الترددي هذا بعد ذلك حدود التكامل الخاصة بنا\(dr\)، أي أننا ندمج من\(r = 0\) إلى\(r = R\). بتجميع كل هذا معًا، لدينا
\[\begin{split} I & = \int_{0}^{R} r^{2} \sigma (2 \pi r) dr = 2 \pi \sigma \int_{0}^{R} r^{3} dr = 2 \pi \sigma \frac{r^{4}}{4} \Big|_{0}^{R} \\ & = 2 \pi \sigma \left(\dfrac{R^{4}}{4} - 0 \right) = 2 \pi \left(\dfrac{m}{A}\right) \left(\dfrac{R^{4}}{4}\right) = 2 \pi \left(\dfrac{m}{\pi R^{2}}\right) \left(\dfrac{R^{4}}{4}\right) = \frac{1}{2} mR^{2} \ldotp \end{split}\]
لاحظ أن هذا يتوافق مع القيمة الواردة في الشكل 10.5.4.
حساب لحظة القصور الذاتي للأجسام المركبة
الآن ضع في اعتبارك كائنًا مركبًا مثل ذلك الموجود في الشكل\(\PageIndex{6}\)، والذي يصور قرصًا رقيقًا في نهاية قضيب رقيق. لا يمكن دمج هذا بسهولة للعثور على لحظة القصور الذاتي لأنه ليس كائنًا ذا شكل موحد. ومع ذلك، إذا عدنا إلى التعريف الأولي للحظة القصور الذاتي كخلاصة، يمكننا أن نستنتج أنه يمكن العثور على لحظة القصور الذاتي للكائن المركب من مجموع كل جزء من الكائن:
\[I_{total} = \sum_{i} I_{i} \ldotp \label{10.21}\]
من المهم ملاحظة أن لحظات القصور الذاتي للكائنات في المعادلة\(\PageIndex{6}\) تدور حول محور مشترك. في حالة هذا الكائن، سيكون ذلك قضيبًا طوله L يدور حول نهايته، وقرص رقيق نصف قطره\(R\) يدور حول محور\(R\) يتم إزاحته عن المركز بمسافة\(L + R\)، أين نصف قطر القرص. دعونا نحدد كتلة القضيب لتكون m r وكتلة القرص المراد أن تكون\(m_d\).
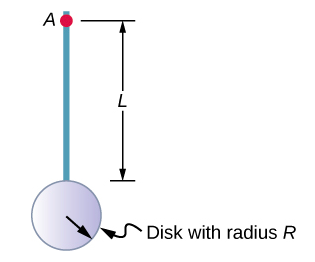
إن لحظة القصور الذاتي للقضيب هي ببساطة\(\frac{1}{3} m_rL^2\)، ولكن علينا استخدام نظرية المحور المتوازي لإيجاد لحظة القصور الذاتي للقرص حول المحور الموضح. إن لحظة القصور الذاتي للقرص حول مركزه هي\(\frac{1}{2} m_dR^2\) ونحن نطبق نظرية المحور المتوازي (المعادلة\ ref {10.20}) للعثور عليه
\[I_{parallel-axis} = \frac{1}{2} m_{d} R^{2} + m_{d} (L + R)^{2} \ldotp\]
بإضافة لحظة القصور الذاتي للقضيب بالإضافة إلى لحظة القصور الذاتي للقرص مع محور الدوران المتحول، نجد لحظة القصور الذاتي للكائن المركب
\[I_{total} = \frac{1}{3} m_{r} L^{2} + \frac{1}{2} m_{d} R^{2} + m_{d} (L + R)^{2} \ldotp\]
تطبيق حسابات لحظة القصور الذاتي لحل المشكلات
الآن دعونا نفحص بعض التطبيقات العملية لحسابات لحظة القصور الذاتي.
يقف طفل وزنه 25 كجم على مسافة\(r = 1.0\, m\) من محور جولة مرح دوارة (الشكل\(\PageIndex{7}\)). يمكن تقريب مسار الزئبق في صورة قرص صلب منتظم كتلته ٥٠٠ كجم ونصف قطره ٢٫٠ م، فأوجد لحظة القصور الذاتي لهذا النظام.
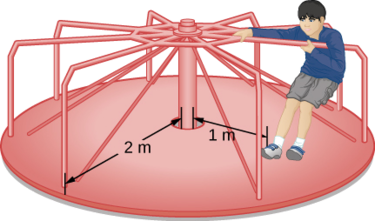
إستراتيجية
تتضمن هذه المشكلة حساب لحظة القصور الذاتي. يتم إعطاؤنا الكتلة والمسافة إلى محور دوران الطفل بالإضافة إلى كتلة ونصف قطر جولة المرح. نظرًا لأن كتلة الطفل وحجمه أصغر بكثير من كتلة المرح، يمكننا تقريب الطفل ككتلة نقطية. الترميز الذي نستخدمه هو m c = 25 كجم، r c = 1.0 م، m = 500 كجم، r m = 2.0 م، هدفنا هو إيجاد\(I_{total} = \sum_{i} I_{i}\) (المعادلة\ ref {10.21}).
الحل
من أجل الطفل\(I_c = m_cr^2\)، ومن أجل جولة المرح،\(I_m = \frac{1}{2}m_m r^2\). لذلك
\[I_{total} = 25(1)^{2} + \frac{1}{2} (500)(2)^{2} = 25 + 1000 = 1025\; kg\; \cdotp m^{2} \ldotp \nonumber \]
الأهمية
يجب أن تكون القيمة قريبة من لحظة القصور الذاتي لجولة المرح في حد ذاتها لأنها تحتوي على كتلة أكبر بكثير موزعة بعيدًا عن المحور مقارنة بالطفل.
ابحث عن لحظة القصور الذاتي لمزيج القضيب والكرة الصلبة حول المحورين كما هو موضح أدناه. يبلغ طول القضيب 0.5 متر وكتلته 2.0 كجم. نصف قطر الكرة يساوي ٢٠٫٠ سم وكتلتها ١٫٠ كجم.
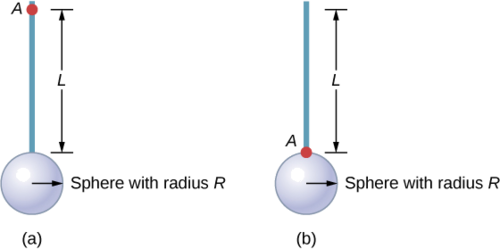
إستراتيجية
بما أن لدينا جسمًا مركبًا في كلتا الحالتين، يمكننا استخدام نظرية المحور المتوازي لإيجاد لحظة القصور الذاتي حول كل محور. في (أ)، يقع مركز كتلة الكرة على مسافة\(L + R\) من محور الدوران. في (ب)، يقع مركز كتلة الكرة على مسافة\(R\) من محور الدوران. في كلتا الحالتين، تكون لحظة القصور الذاتي للقضيب حوالي محور في أحد طرفيه. راجع الجدول 10.4 لمعرفة لحظات القصور الذاتي للكائنات الفردية.
أ.
\[\begin{split} I_{total} & = \sum_{i} I_{i} = I_{Rod} + I_{Sphere}; \\ I_{Sphere} & = I_{center\; of\; mass} + m_{Sphere} (L + R)^{2} = \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} (L + R)^{2}; \\ I_{total} & = I_{Rod} + I_{Sphere} = \frac{1}{3} m_{Rod} L^{2} + \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} (L + R)^{2}; \\ I_{total} & = \frac{1}{3} (20\; kg)(0.5\; m)^{2} + \frac{2}{5} (1.0\; kg)(0.2\; m)^{2} + (1.0\; kg)(0.5\; m + 0.2\; m)^{2}; \\ I_{total} & = (0.167 + 0.016 + 0.490)\; kg\; \cdotp m^{2} = 0.673\; kg\; \cdotp m^{2} \ldotp \end{split}\]
ب.
\[\begin{split} I_{Sphere} & = \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} R^{2}; \\ I_{total} & = I_{Rod} + I_{Sphere} = \frac{1}{3} m_{Rod} L^{2} + \frac{2}{5} (1.0\; kg)(0.2\; m)^{2} + (1.0\; kg)(0.2\; m)^{2}; \\ I_{total} & = (0.167 + 0.016 + 0.04)\; kg\; \cdotp m^{2} = 0.223\; kg\; \cdotp m^{2} \ldotp \end{split}\]
الأهمية
يؤدي استخدام نظرية المحور المتوازي إلى تسهيل حساب لحظة القصور الذاتي للأجسام المركبة. نرى أن لحظة الجمود أكبر في (أ) من (ب). هذا لأن محور الدوران أقرب إلى مركز كتلة النظام في (ب). التشبيه البسيط هو القضيب. لحظة القصور الذاتي حول أحد الطرفين هي\(\frac{1}{3}\) mL 2، لكن لحظة القصور الذاتي عبر مركز الكتلة بطولها هي\(\frac{1}{12}\) mL 2.
يتم تحرير بندول على شكل قضيب (الشكل\(\PageIndex{8}\)) من السكون بزاوية 30 درجة. يبلغ طوله ٣٠ سم وكتلته ٣٠٠ جم، ما سرعته الزاوية عند أدنى نقطة له؟
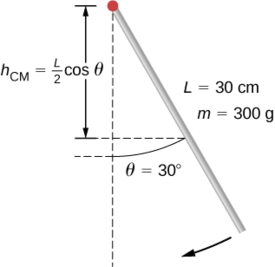
إستراتيجية
استخدم الحفاظ على الطاقة لحل المشكلة. عند نقطة الإطلاق، يحتوي البندول على طاقة كامنة للجاذبية، والتي يتم تحديدها من ارتفاع مركز الكتلة فوق أدنى نقطة في الأرجوحة. في الجزء السفلي من الأرجوحة، يتم تحويل كل طاقة الجاذبية الكامنة إلى طاقة حركية دورانية.
الحل
التغيير في الطاقة الكامنة يساوي التغيير في الطاقة الحركية الدورانية\(\Delta U + \Delta K = 0\).
في الجزء العلوي من الأرجوحة:
\[U = mgh_{cm} = mgL^2 (\cos \theta). \nonumber \]
في الجزء السفلي من الأرجوحة،
\[U = mg \frac{L}{2}. \nonumber\]
في الجزء العلوي من الأرجوحة، تكون طاقة الحركة الدورانية K = 0. في الجزء السفلي من الأرجوحة، K =\(\frac{1}{2} I \omega^{2}\). لذلك:
\[\Delta U + \Delta K = 0 \Rightarrow (mg \frac{L}{2} (1 - \cos \theta) - 0) + (0 - \frac{1}{2} I \omega^{2}) = 0 \nonumber\]
أو
\[\frac{1}{2} I \omega^{2} = mg \frac{L}{2} (1 - \cos \theta) \ldotp \nonumber\]
حل المشكلة\(\omega\)، لدينا
\[\omega = \sqrt{mg \frac{L}{I} (1 - \cos \theta)} = \sqrt{mg \frac{L}{\frac{1}{3} mL^{2}} (1 - \cos \theta)} = \sqrt{g \frac{3}{L} (1 - \cos \theta)} \ldotp \nonumber\]
إدراج القيم العددية، لدينا
\[\omega = \sqrt{(9.8\; m/s^{2}) \left(\dfrac{3}{0.3\; m}\right) (1 - \cos 30)} = 3.6\; rad/s \ldotp \nonumber\]
الأهمية
لاحظ أن السرعة الزاوية للبندول لا تعتمد على كتلته.


