6.5: الاحتكاك (الجزء 2)
- Page ID
- 200078
الاحتكاك والمستوى المائل
إحدى الحالات التي يلعب فيها الاحتكاك دورًا واضحًا هي حالة كائن على منحدر. قد يكون صندوقًا يتم دفعه لأعلى منحدر إلى رصيف تحميل أو لوح تزلج يتزلج على جبل، لكن الفيزياء الأساسية هي نفسها. عادة ما نقوم بتعميم السطح المنحدر ونطلق عليه اسم المستوى المائل ولكن بعد ذلك نتظاهر بأن السطح مسطح. لنلقِ نظرة على مثال لتحليل الحركة على مستوى مائل مع الاحتكاك.
متزلج كتلته ٦٢ كجم ينزلق إلى أسفل منحدر ثلجي بسرعة ثابتة. أوجد معامل الاحتكاك الحركي للمتزلج إذا كان الاحتكاك معروفًا بـ 45.0 N.
إستراتيجية
مقدار الاحتكاك الحركي هو 45.0 نيوتن. الاحتكاك الحركي مرتبط بالقوة العادية N بمقدار f k =\(\mu_{k}\) N؛ وبالتالي، يمكننا إيجاد معامل الاحتكاك الحركي إذا تمكنا من إيجاد القوة العادية على المتزلج. دائمًا ما تكون القوة العادية متعامدة على السطح، ونظرًا لعدم وجود حركة عمودية على السطح، يجب أن تساوي القوة العادية مكون وزن المتزلج عموديًا على المنحدر. (راجع الشكل\(\PageIndex{1}\) الذي يكرر شكلاً من الفصل الخاص بقوانين نيوتن للحركة.)
لدينا
\[N = w_{y} = w \cos 25^{o} = mg \cos 25^{o} \ldotp\]
باستبدال هذا في تعبيرنا بالاحتكاك الحركي، نحصل على
\[f_{k} = \mu_{k} mg \cos 25^{o},\]
والتي يمكن حلها الآن لمعامل الاحتكاك الحركي\(\mu_{k}\).
الحل
حل\(\mu_{k}\) للعطاء
\[\mu_{k} = \frac{f_{k}}{N} = \frac{f_{k}}{w \cos 25^{o}} = \frac{f_{k}}{mg \cos 25^{o}} \ldotp\]
استبدال القيم المعروفة على الجانب الأيمن من المعادلة،
\[\mu_{k} = \frac{45.0\; N}{(62\; kg)(9.80\; m/s^{2})(0.906)} = 0.082 \ldotp\]
الدلالة
هذه النتيجة أصغر قليلاً من المعامل المدرج في الجدول 6.1 للخشب المشمع على الثلج، لكنها لا تزال معقولة لأن قيم معاملات الاحتكاك يمكن أن تختلف اختلافًا كبيرًا. في مثل هذه الحالات، عندما ينزلق جسم كتلته m إلى أسفل منحدر يصنع زاوية\(\theta\) بزاوية أفقية، يتم إعطاء الاحتكاك بواسطة f k =\(\mu_{k}\) mg cos\(\theta\). تنزلق جميع الكائنات إلى أسفل منحدر مع تسارع مستمر في ظل هذه الظروف.
لقد ناقشنا أنه عندما يستقر جسم على سطح أفقي، فإن القوة الطبيعية التي تدعمه تساوي في الحجم وزنه. علاوة على ذلك، فإن الاحتكاك البسيط يتناسب دائمًا مع القوة العادية. عندما لا يكون الجسم على سطح أفقي، كما هو الحال مع المستوى المائل، يجب أن نجد القوة المؤثرة على الجسم الموجه عموديًا على السطح؛ إنه أحد مكونات الوزن.
نستمد الآن علاقة مفيدة لحساب معامل الاحتكاك على مستوى مائل. لاحظ أن النتيجة تنطبق فقط على الحالات التي ينزلق فيها الكائن بسرعة ثابتة أسفل المنحدر.
يتحرك جسم لأسفل مستوًى مائل بسرعة ثابتة إذا كانت القوة الكلية المؤثِّرة على الجسم تساوي صفرًا. يمكننا استخدام هذه الحقيقة لقياس معامل الاحتكاك الحركي بين جسمين. كما هو موضح في المثال\(\PageIndex{1}\)، الاحتكاك الحركي على المنحدر هو f k =\(\mu_{k}\) mg cos\(\theta\). إن مكون الوزن الموجود أسفل المنحدر يساوي mg sin\(\theta\) (انظر مخطط الجسم الحر في الشكل\(\PageIndex{1}\)). تعمل هذه القوى في اتجاهين متعاكسين، لذلك عندما يكون لها حجم متساوٍ، يكون التسارع صفرًا. كتابة هذه،
\[\mu_{k} mg \cos \theta = mg \sin \theta \ldotp\]
لحل المشكلة\(\mu_{k}\)، نجد ذلك
\[\mu_{k} = \frac{mg \sin \theta}{mg \cos \theta} = \tan \theta \ldotp\]
ضع عملة معدنية على كتاب وقم بإمالتها حتى تنزلق العملة بسرعة ثابتة أسفل الكتاب. قد تحتاج إلى النقر على الكتاب برفق لتحريك العملة. قم بقياس زاوية الميل بالنسبة للأفقي وابحث عنها\(\mu_{k}\). لاحظ أن العملة لا تبدأ في الانزلاق على الإطلاق حتى زاوية أكبر من تلك التي\(\theta\) يتم تحقيقها، لأن معامل الاحتكاك الإستاتيكي أكبر من معامل الاحتكاك الحركي. فكر في كيفية تأثير ذلك على القيمة\(\mu_{k}\) وعدم اليقين.
تفسيرات الاحتكاك بالمقياس الذري
الجوانب الأبسط للاحتكاك التي تم التعامل معها حتى الآن هي خصائصه العيانية (واسعة النطاق). لقد تم اتخاذ خطوات كبيرة في تفسير النطاق الذري للاحتكاك خلال العقود العديدة الماضية. وجد الباحثون أن الطبيعة الذرية للاحتكاك يبدو أن لها العديد من الخصائص الأساسية. لا تفسر هذه الخصائص بعض الجوانب البسيطة للاحتكاك فحسب، بل إنها تنطوي أيضًا على إمكانية تطوير بيئات خالية من الاحتكاك تقريبًا يمكن أن توفر مئات المليارات من الدولارات من الطاقة التي يتم تحويلها حاليًا (دون داع) إلى حرارة.
\(\PageIndex{2}\)يوضح الشكل إحدى الخصائص العيانية للاحتكاك التي يتم تفسيرها من خلال البحث المجهري (صغير النطاق). لقد لاحظنا أن الاحتكاك يتناسب مع القوة العادية، ولكن ليس مع مقدار مساحة الاتصال، وهي فكرة غير بديهية إلى حد ما. عند ملامسة سطحين خشنين، تكون منطقة التلامس الفعلية جزءًا صغيرًا من المساحة الكلية لأن البقع العالية فقط تتلامس. عند ممارسة قوة طبيعية أكبر، تزداد منطقة التلامس الفعلية، ونجد أن الاحتكاك يتناسب مع هذه المنطقة.
ومع ذلك، فإن وجهة النظر ذات المقياس الذري تعد بشرح أكثر بكثير من السمات الأبسط للاحتكاك. يتم الآن تحديد آلية كيفية توليد الحرارة. بعبارة أخرى، لماذا تصبح الأسطح أكثر دفئًا عند فركها؟ بشكل أساسي، ترتبط الذرات ببعضها البعض لتشكيل المشابك. عندما تفرك الأسطح، تلتصق ذرات السطح وتتسبب في اهتزاز المشابك الذرية - مما يؤدي أساسًا إلى إنشاء موجات صوتية تخترق المادة. تتناقص الموجات الصوتية مع المسافة، وتتحول طاقتها إلى حرارة. يمكن أن تحدث التفاعلات الكيميائية المرتبطة بالتآكل الاحتكاكي أيضًا بين الذرات والجزيئات على الأسطح. \(\PageIndex{3}\)يوضح الشكل كيف يتشوه طرف المسبار المسحوب عبر مادة أخرى بسبب الاحتكاك بالمقياس الذري. يمكن قياس القوة اللازمة لسحب الطرف ووجد أنها مرتبطة بإجهاد القص، وهو ما تمت مناقشته في التوازن الثابت والمرونة. يعد التباين في إجهاد القص ملحوظًا (أكثر من عامل 1012) ويصعب التنبؤ به نظريًا، لكن إجهاد القص ينتج فهمًا أساسيًا لظاهرة واسعة النطاق معروفة منذ العصور القديمة - الاحتكاك.
وصف نموذج الاحتكاك على المستوى الجزيئي. وصف المادة من حيث الحركة الجزيئية. يجب أن يتضمن الوصف مخططات لدعم الوصف؛ وكيفية تأثير درجة الحرارة على الصورة؛ وما هي الاختلافات والتشابهات بين حركة الجسيمات الصلبة والسائلة والغازية؛ وكيفية ارتباط حجم وسرعة جزيئات الغاز بالأشياء اليومية.
\(\PageIndex{4}\)يتم ربط الكتلتين في الشكل ببعضهما البعض بواسطة خيط بدون كتلة ملفوف حول بكرة خالية من الاحتكاك. عندما يتم سحب الكتلة السفلية التي يبلغ وزنها 4.00 كجم إلى اليسار بالقوة الثابتة\(\vec{P}\)، تنزلق الكتلة العلوية التي يبلغ وزنها 2.00 كجم عبرها إلى اليمين. أوجد مقدار القوة اللازمة لتحريك الكتل بسرعة ثابتة. افترض أن معامل الاحتكاك الحركي بين جميع الأسطح يساوي 0.400.
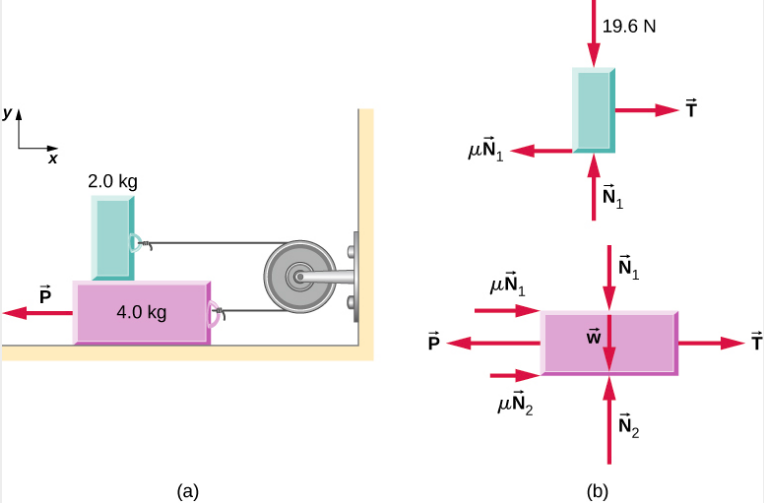
إستراتيجية
نقوم بتحليل حركات الكتلتين بشكل منفصل. تتعرض الكتلة العلوية لقوة التلامس التي تمارسها الكتلة السفلية. مكونات هذه القوة هي القوة العادية N 1 وقوة الاحتكاك −0.400 N 1. القوى الأخرى الموجودة على الكتلة العلوية هي الشد T في الخيط ووزن الكتلة العلوية نفسها، 19.6 نيوتن. تتعرض الكتلة السفلية لقوى التلامس بسبب الكتلة العلوية وبسبب الأرضية. تحتوي قوة الاتصال الأولى على المكونين −N 1 و 0.400 N 1، وهما ببساطة قوى رد فعل لقوى التلامس التي تمارسها الكتلة السفلية على الكتلة العلوية. مكونات قوة التلامس للأرضية هي N 2 و 0.400 N 2. القوى الأخرى التي تؤثر على هذه الكتلة هي −P والشد T والوزن —39.2 نيوتن. ونظرًا لأن الكتلة العلوية تتحرك أفقيًا إلى اليمين بسرعة ثابتة، فإن عجلتها تساوي صفرًا في كلا الاتجاهين الأفقي والعمودي. من قانون نيوتن الثاني،
|
\[\sum F_{x} = m_{2} a_{x}\] \[T - 0.400\; N_{1} = 0\] |
\[\sum F_{y} = m_{1} a_{y}\] \[N_{1} - 19.6\; N = 0 \ldotp\] |
لحل المشكلتين المجهولتين، نحصل على N 1 = 19.6 N و T = 0.40 N 1 = 7.84 N. الكتلة السفلية لا تتسارع أيضًا، لذا فإن تطبيق قانون نيوتن الثاني على هذه الكتلة يعطي
|
\[\sum F_{x} = m_{2} a_{x}\] \[T - P + 0.400\; N_{1} + 0.400\; N_{2} = 0\] |
\[\sum F_{y} = m_{1} a_{y}\] \[N_{2} - 39.2\; N - N_{1} = 0 \ldotp\] |
تم العثور على قيم N 1 و T مع المجموعة الأولى من المعادلات. عندما يتم استبدال هذه القيم في المجموعة الثانية من المعادلات، يمكننا تحديد N 2 و P. وهي
\[N_{2} = 58.8\; N\; and\; P = 39.2\; N \ldotp\]
الدلالة
غالبًا ما يكون فهم الاتجاه الذي يتم فيه سحب قوة الاحتكاك أمرًا مزعجًا. لاحظ أن كل قوة احتكاك موضحة في الشكل\(\PageIndex{4}\) تعمل في الاتجاه المعاكس لحركة الكتلة المقابلة لها.
يقع صندوق وزنه 50.0 كجم على سرير شاحنة كما هو موضح في الشكل\(\PageIndex{5}\). معاملات الاحتكاك بين الأسطح هي\(\mu_{k}\) = 0.300 و\(\mu_{s}\) = 0.400. أوجد قوة الاحتكاك المؤثِّرة على الصندوق عندما تتسارع الشاحنة إلى الأمام بالنسبة إلى الأرض بسرعة (أ) ٢٫٠٠ م/ث ٢، (ب) ٥٫٠٠ م/ث ٢.
إستراتيجية
القوى الموجودة على الصندوق هي وزنه والقوى العادية والاحتكاكية بسبب ملامسته لسرير الشاحنة. نبدأ بافتراض أن الصندوق لا ينزلق. في هذه الحالة، تعمل قوة الاحتكاك الثابتة fs على الصندوق. علاوة على ذلك، تتساوى معدلات التسارع في الصندوق والشاحنة.
الحل
- تطبيق قانون نيوتن الثاني على الصندوق، باستخدام الإطار المرجعي المرفق بالأرض، ينتج
\[\begin{split} \sum F_{x} & = ma_{x} \\ f_{s} & = (50.0\; kg)(2.00\; m/s^{2}) \\ & = 1.00 \times 10^{2}\; N \end{split}\]
\[\begin{split} \sum F_{y} & = ma_{y} \\ N - 4.90 \times 10^{2}\; N & = (50.0\; kg)(0) \\ N & = 4.90 \times 10^{2}\; N \ldotp \end{split}\]
يمكننا الآن التحقق من صحة افتراض عدم الانزلاق. القيمة القصوى لقوة الاحتكاك الإستاتيكي هي $$\ mu_ {s} N = (0.400) (4.90\ مرات 10^ {2}\; N) = 196\; N, $في حين أن القوة الفعلية للاحتكاك الإستاتيكي الذي يعمل عندما تتسارع الشاحنة للأمام بسرعة 2.00 متر/ثانية 2 هي 1.00 × 10 2 نيوتن فقط، وبالتالي فإن افتراض عدم الانزلاق صالحة.
- إذا كان الصندوق سيتحرك مع الشاحنة عندما تتسارع بسرعة 5.0 متر/ثانية 2، يجب أن تكون قوة الاحتكاك الإستاتيكي $$f_ {s} = ma_ {x} = (50.0\; kg) (5.00\; m/s^ {2}) = 250\; N\ lDotP$$نظرًا لأن هذا يتجاوز الحد الأقصى البالغ 196 نيوتن، يجب أن ينزلق الصندوق. لذلك تكون قوة الاحتكاك حركية وهي $$f_ {k} =\ mu_ {k} N = (0.300) (4.90\ مرات 10^ {2}\; N) = 147\; N\ lDotP$تم العثور الآن على التسارع الأفقي للصندوق بالنسبة للأرض من $$\ البدء {الانقسام}\\ المجموع F_ {x} & = ma_ {x}\\ 147\; N & = (50.0\؛ كجم) a_ {x}،\\ هكذا\؛ a_ {x} & = 2.94\؛ م/ث ^ {2}\ ldotp\ end {الانقسام}\]
الدلالة
بالنسبة إلى الأرض، تتسارع الشاحنة للأمام بسرعة 5.0 متر/ثانية 2 ويتسارع الصندوق للأمام بسرعة 2.94 متر/ثانية 2. ومن ثم فإن الصندوق ينزلق للخلف بالنسبة إلى سرير الشاحنة بسرعة 2.94 م/ث 2 − 5.00 م/ث 2 = −2.06 م/ث 2.
في وقت سابق، قمنا بتحليل حالة متزلج منحدر يتحرك بسرعة ثابتة لتحديد معامل الاحتكاك الحركي. الآن دعونا نقوم بتحليل مماثل لتحديد التسارع. \(\PageIndex{6}\)تنزلق أداة التزحلق على الجليد في الشكل إلى أسفل منحدر يميل عند\(\theta\) = 13 درجة إلى الأفقي. معامل الاحتكاك الحركي بين اللوح والثلج هو\(\mu_{k}\) = 0.20. ما هو تسارع المتزلج على الجليد؟
إستراتيجية
القوى المؤثرة على المتزلجة هي وزنها وقوة التلامس للمنحدر، والتي تحتوي على مكون طبيعي للمنحدر ومكون على طول المنحدر (قوة الاحتكاك الحركي). ونظرًا لأنها تتحرك على طول المنحدر، فإن الإطار المرجعي الأكثر ملاءمة لتحليل حركتها هو الإطار الذي يكون فيه المحور السيني على طول المحور الصادي عموديًا على المنحدر. في هذا الإطار، تكمن كل من القوى العادية والقوى الاحتكاكية على طول محاور الإحداثيات، ومكونات الوزن هي mg sin على طول المنحدر و mg cos\(\theta\) عند الزوايا اليمنى للمنحدر، ويكون التسارع الوحيد على طول المحور السيني (a y = 0).
الحل
يمكننا الآن تطبيق قانون نيوتن الثاني على المتزلج على الجليد:
|
\[\begin{split} \sum F_{x} & = ma_{x} \\ mg \sin \theta - \mu_{k} N & = ma_{x} \end{split}\] |
\[\begin{split} \sum F_{y} & = ma_{y} \\ N - mg \cos \theta &= m(0) \ldotp \end{split}\] |
من المعادلة الثانية، N = mg cos\(\theta\). عند استبدال هذا بالمعادلة الأولى، نجد
\[\begin{split} a_{x} & = g(\sin \theta - \mu_{k} \cos \theta) \\ & = g(\sin 13^{o} - 0.520 \cos 13^{o}) = 0.29\; m/s^{2} \ldotp \end{split}\]
الدلالة
لاحظ من هذه المعادلة أنه إذا كانت\(\theta\) صغيرة بما\(\mu_{k}\) يكفي أو كبيرة بما يكفي، فإن x تكون سالبة، أي أن المتزلج على الجليد يتباطأ.
يتحرك المتزلج الآن إلى أسفل تل منحدر بزاوية 10.0 درجة. ما هو تسارع المتزلج؟


