4.2: متجهات الإزاحة والسرعة

Last updated
Save as PDF

Page ID: 200029

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

احسب متجهات الموضع في مشكلة الإزاحة متعددة الأبعاد.
حل الإزاحة في بعدين أو ثلاثة أبعاد.
احسب متجه السرعة بمعلومية متجه الموضع كدالة للوقت.
احسب السرعة المتوسطة بأبعاد متعددة.

الإزاحة والسرعة في بعدين أو ثلاثة هي امتدادات مباشرة للتعريفات أحادية البعد. ومع ذلك، فهي الآن كميات متجهة، لذا يجب أن تتبع الحسابات معها قواعد الجبر المتجه، وليس الجبر العددي.

ناقل الإزاحة

لوصف الحركة في بعدين وثلاثة أبعاد، يجب علينا أولاً إنشاء نظام إحداثيات واتفاقية للمحاور. نحن نستخدم الإحداثيات بشكل عام$x$$y$،$z$ ولتحديد موقع الجسيم عند نقطة$P(x, y, z)$ في ثلاثة أبعاد. إذا كان الجسيم يتحرك، فإن المتغيرات$x$$y$،$z$ وهي وظائف الوقت ($t$):

\[x = x(t) \quad y = y(t) \quad z = z(t) \ldotp \label{4.1}\]

متجه الموضع من أصل نظام الإحداثيات إلى النقطة P هو$\vec{r}(t)$. في ترميز متجه الوحدة، الذي تم تقديمه في أنظمة الإحداثيات ومكونات المتجه،$\vec{r}$ (t) هو

\[\vec{r} (t) = x(t)\; \hat{i} + y(t)\; \hat{j} + z(t)\; \hat{k} \ldotp \label{4.2}\]

$\PageIndex{1}$يوضح الشكل نظام الإحداثيات والمتجه إلى النقطة$P$، حيث يمكن تحديد موقع الجسيم في وقت معين$t$. لاحظ اتجاه المحاور x و y و z. يُطلق على هذا الاتجاه اسم نظام الإحداثيات الأيمن ويتم استخدامه في جميع أنحاء الفصل.

يظهر نظام الإحداثيات x y z، مع وجود علامة x موجبة خارج الصفحة، وإيجابية y على اليمين، وإيجابية z لأعلى. يتم عرض النقطة P، مع الإحداثيات x من t، y من t، و z من t. جميع إحداثيات P إيجابية. يظهر المتجه r of t من الأصل إلى P أيضًا كسهم أرجواني. تظهر الإحداثيات x من t و y من t و z من t كخطوط متقطعة. X of t هو مقطع في المستوى x y، موازٍ للمحور x، y of t هو مقطع في المستوى x y، موازٍ للمحور y، و z of t هو مقطع موازٍ للمحور z. — الشكل$\PageIndex{1}$: نظام إحداثيات ثلاثي الأبعاد بجسيم في موضعه$P(x(t), y(t), z(t))$.

من خلال تعريفنا لموضع الجسيم في الفضاء ثلاثي الأبعاد، يمكننا صياغة الإزاحة ثلاثية الأبعاد. $\PageIndex{3}$يوضح الشكل جسيمًا في الوقت t ₁ يقع عند P ₁ مع متجه الموضع$\vec{r}$ (t ₁). في وقت لاحق عند ₂، يقع الجسيم عند P ₂ مع متجه الموضع$\vec{r}$ (t ₂). تم العثور على$\Delta \vec{r}$ متجه الإزاحة عن طريق الطرح$\vec{r}(t_1)$ من$\vec{r}(t_2)$:

\[\Delta \vec{r} = \vec{r} (t_{2}) - \vec{r} (t_{1}) \ldotp \label{4.3}\]

تمت مناقشة إضافة المتجهات في Vectors. لاحظ أن هذه هي نفس العملية التي قمنا بها في بُعد واحد، ولكن المتجهات الآن في الفضاء ثلاثي الأبعاد.

يظهر نظام الإحداثيات x y z، مع وجود علامة x موجبة خارج الصفحة، وإيجابية y على اليمين، وإيجابية z لأعلى. يتم عرض نقطتين، P 1 و P 2. يتم عرض المتجه r لـ t 1 من الأصل إلى P 1 والمتجه r لـ t 2 من الأصل إلى P 2 كأسهم أرجوانية. يظهر المتجه delta r كسهم أرجواني يكون ذيله عند P 1 ويتجه إلى P 2. — الشكل$\PageIndex{2}$: الإزاحة$\Delta \vec{r} = \vec{r}(t_2) − \vec{r}(t_1)$ هي المتجه من$P_1$ إلى$P_2$.

توضح الأمثلة التالية مفهوم النزوح بأبعاد متعددة

مثال 4.1: القمر الصناعي ذو المدار القطبي

يوجد القمر الصناعي في مدار قطبي دائري حول الأرض على ارتفاع 400 كم - أي أنه يمر مباشرة فوق القطبين الشمالي والجنوبي. ما مقدار متجه الإزاحة واتجاهه عندما يكون مباشرةً فوق القطب الشمالي حتى عند خط العرض −45°؟

إستراتيجية

نقوم بعمل صورة للمشكلة لتصور الحل بيانياً. هذا سوف يساعد في فهمنا للنزوح. ثم نستخدم متجهات الوحدة لحل الإزاحة.

الحل

$\PageIndex{3}$يوضِّح الشكل سطح الأرض والدائرة التي تُمثِّل مدار القمر الصناعي. على الرغم من أن الأقمار الصناعية تتحرك في الفضاء ثلاثي الأبعاد، إلا أنها تتبع مسارات القطع الناقص، والتي يمكن رسمها بيانيًا في بعدين. يتم رسم متجهات الموضع من مركز الأرض، والذي نعتبره أصل نظام الإحداثيات، حيث يكون المحور y شمالًا والمحور السيني شرقًا. المتجه بينهما هو نزوح القمر الصناعي. نأخذ نصف قطر الأرض على أنه 6370 كم، وبالتالي فإن طول كل متجه للموضع هو 6770 كم.

يظهر نظام إحداثيات x y، المتمركز على الأرض. علامة x الموجبة هي إلى الشرق والإيجابية y في الشمال. تظهر دائرة زرقاء أكبر من الأرض ومتمركزة معها. Vector r of t 1 هو سهم برتقالي من الأصل إلى الموقع حيث تعبر الدائرة الزرقاء المحور y (90 درجة عكس اتجاه عقارب الساعة من المحور x الموجب.) Vector r of t 2 هو سهم برتقالي من الأصل إلى الموقع على الدائرة الزرقاء عند 45 درجة تحت الصفر. يظهر متجه Delta r كسهم أرجواني يشير لأسفل وإلى اليمين، بدءًا من رأس المتجه r لـ t 1 وينتهي عند رأس المتجه r لـ t 2. — الشكل$\PageIndex{3}$: يتم رسم متجهين للموضع من مركز الأرض، وهو أصل نظام الإحداثيات، حيث يكون المحور y شمالًا والمحور السيني شرقًا. المتجه بينهما هو نزوح القمر الصناعي.

في ترميز متجه الوحدة، تكون متجهات الموضع هي

\[ \begin{align*} \vec{r}(t_{1}) &= 6770 \ldotp \; km\; \hat{j} \\[4pt] \vec{r}(t_{2}) &= 6770 \ldotp \; km (\cos (-45°))\; \hat{i} + 6770 \ldotp \; km (\sin(−45°))\; \hat{j} \ldotp \end{align*}\]

تقييم العمود الفقري وجيب التمام، لدينا

\[ \begin{align*} \vec{r}(t_{1}) &= 6770 \ldotp \hat{j} \\[4pt] \vec{r}(t_{2}) &= 4787\; \hat{i} − 4787\; \hat{j} \ldotp \end{align*}\]

الآن يمكننا أن نجد$\Delta \vec{r}$، نزوح القمر الصناعي:

\[\Delta \vec{r} = \vec{r} (t_{2}) - \vec{r} (t_{1}) = 4787\; \hat{i} - 11,557\; \hat{j} \ldotp \nonumber\]

حجم النزوح هو

\[|\Delta \vec{r}| = \sqrt{(4787)^{2} + (-11,557)^{2}} = 12,509\; km. \nonumber\]

الزاوية التي تصنعها الإزاحة مع المحور السيني هي

\[\theta = \tan^{-1} \left(\dfrac{-11,557}{4787}\right) = -67.5^{o} \nonumber.\]

الدلالة

يعطي تخطيط الإزاحة معلومات ومعنى لحل متجه الوحدة للمشكلة. عند تخطيط الإزاحة، نحتاج إلى تضمين مكوناتها بالإضافة إلى حجمها والزاوية التي تصنعها بالمحور المختار - في هذه الحالة، المحور السيني (الشكل$\PageIndex{4}$).

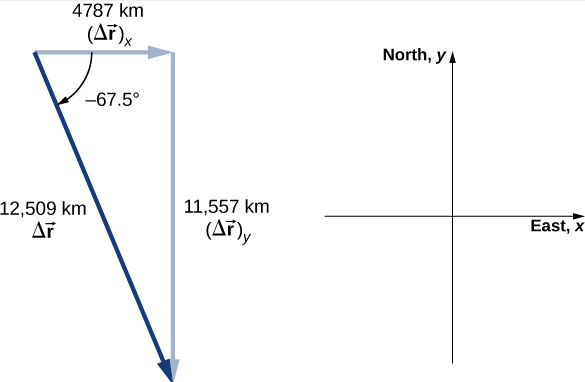
يتم عرض نظام إحداثيات x y. علامة x الموجبة هي إلى الشرق والإيجابية y في الشمال. يشير متجه دلتا r sub x إلى الشرق ويبلغ حجمه 4787 كيلومترًا. يشير ناقل دلتا r sub y إلى الجنوب ويبلغ حجمه 11,557 كيلومترًا. يشير المتجه دلتا r إلى الجنوب الشرقي، بدءًا من ذيل دلتا r sub x وينتهي عند رأس دلتا r sub y ويبلغ حجمه 12,509 كيلومترًا. — الشكل$\PageIndex{4}$: متجه الإزاحة بالمكونات والزاوية والحجم.

لاحظ أن القمر الصناعي اتخذ مسارًا منحنيًا على طول مداره الدائري للانتقال من موضعه الأولي إلى موضعه النهائي في هذا المثال. كان من الممكن أيضًا أن تقطع 4787 كيلومترًا شرقًا، ثم 11,557 كيلومترًا جنوبًا للوصول إلى نفس الموقع. كلا المسارين أطول من طول متجه الإزاحة. في الواقع، يعطي متجه الإزاحة أقصر مسار بين نقطتين في أبعاد واحدة أو اثنتين أو ثلاثة أبعاد.

يمكن أن تحتوي العديد من التطبيقات في الفيزياء على سلسلة من عمليات الترحيل، كما تمت مناقشته في الفصل السابق. إجمالي النزوح هو مجموع عمليات النزوح الفردية، ولكن هذه المرة فقط، نحتاج إلى توخي الحذر، لأننا نضيف ناقلات. نوضح هذا المفهوم بمثال للحركة البراونية.

مثال 4.2: الحركة البراونية

الحركة البراونية هي حركة عشوائية فوضوية للجسيمات العالقة في السائل، الناتجة عن التصادمات بجزيئات السائل. هذه الحركة ثلاثية الأبعاد. يمكن أن تبدو عمليات النزوح بالترتيب العددي لجسيم يمر بحركة براونية كما يلي، بالميكرومتر (الشكل$\PageIndex{5}$):

\[\Delta \vec{r}_{1} = 2.0\; \hat{i} + \hat{j} + 3.0 \hat{k}\]

\[\Delta \vec{r}_{2} = - \hat{i} + 3.0\; \hat{k}\]

\[\Delta \vec{r}_{3} = 4.0\; \hat{i} -2.0\; \hat{j} + \hat{k}\]

\[\Delta \vec{r}_{4} = -3.0\; \hat{i} + \hat{j} + 3.0\; \hat{k} \ldotp\]

ما الإزاحة الكلية للجسيم من الأصل؟

يتم عرض نظام إحداثيات x y z بمسافات مقاسة بالميكرومتر وتتراوح من -10 إلى +10 ميكرومتر. تساوي عمليات الإزاحة دلتا أو الفرعية 1 2 I hat بالإضافة إلى قبعة j بالإضافة إلى 2 k hat، ودلتا r sub 2 تساوي -1 I hat بالإضافة إلى 3 K قبعة، ودلتا r sub 3 تساوي -3 I hat بالإضافة إلى j hat بالإضافة إلى 2 k التي تظهر كمقاطع خط أزرق. Vector r 1 الذي يبدأ من الأصل. يبدأ كل نزوح لاحق حيث ينتهي السابق. يظهر إجمالي دلتا المتجهات كخط أحمر يبدأ من الأصل وينتهي في نهاية المتجه دلتا r 4. دلتا أو المجموع يساوي 2 درجة مئوية بالإضافة إلى 50 درجة مئوية بالإضافة إلى قبعة 90 كيلو بايت. — الشكل$\PageIndex{5}$: مسار جسيم يخضع لعمليات نزوح عشوائية للحركة البراونية. يظهر إجمالي الإزاحة باللون الأحمر.

الحل

نشكل مجموع عمليات النزوح ونضيفها كمتجهات:

\[\begin{split} \Delta \vec{r}_{Total} & = \sum \Delta \vec{r}_{i} = \Delta \vec{r}_{1} + \Delta \vec{r}_{2} + \Delta \vec{r}_{3} + \Delta \vec{r}_{4} \\ & = (2.0 - 1.0 + 4.0 - 3.0)\; \hat{i} + (1.0 + 0 - 2.0 + 1.0)\; \hat{j} + (3.0 +3.0 + 1.0 + 2.0)\; \hat{k} \\ & = 2.0\; \hat{i} + 0\; \hat{j} + 9.0\; \hat{k}\; \mu m \ldotp \end{split}\]

لإكمال الحل، نعبر عن الإزاحة كحجم واتجاه،

\[| \Delta \vec{r}_{Total}| = \sqrt{2.0^{2} + 0^{2} + 9.0^{2}} = 9.2 \mu m, \quad \theta = \tan^{-1} \left(\dfrac{9}{2}\right) = 77^{o},\]

فيما يتعلق بالمحور السيني في الطائرة xz.

الدلالة

من الشكل يمكننا أن نرى أن حجم النزوح الكلي أقل من مجموع مقادير النزوح الفردي.

ناقل السرعة

في الفصل السابق وجدنا السرعة اللحظية من خلال حساب مشتق دالة الموضع فيما يتعلق بالوقت. يمكننا القيام بنفس العملية في بعدين وثلاثة أبعاد، لكننا نستخدم المتجهات. متجه السرعة اللحظية هو الآن

\[\vec{v} (t) = \lim_{\Delta t \rightarrow 0} \frac{\vec{r} (t + \Delta t) - \vec{r} (t)}{\Delta t} = \frac{d \vec{r}}{dt} \ldotp \label{4.4}\]

دعونا ننظر إلى الاتجاه النسبي لمتجه الموضع ومتجه السرعة بيانياً. $\PageIndex{6}$نعرض في الشكل المتجهين$\vec{r}$ (t) و$\vec{r}$ ($\Delta$t + t)، اللذين يوضحان موضع جسيم يتحرك على طول مسار يمثله الخط الرمادي. عندما تصل$\Delta$ t إلى الصفر، يصبح متجه السرعة، المعطى بواسطة المعادلة\ ref {4.4}، مماسًا لمسار الجسيم في الوقت t.

تظهر المتجهات r of t و r من t بالإضافة إلى دلتا t كأسهم حمراء في نظام الإحداثيات x y. يبدأ كلا المتجهين من نقطة الأصل. يشير المتجه دلتا r من رأس المتجه r of t إلى رأس المتجه r of t إلى رأس المتجه r of t بالإضافة إلى دلتا t. — الشكل$\PageIndex{6}$: يتحرك جسم على طول مسار يحدده الخط الرمادي. في الحد عند اقتراب$\Delta$ t من الصفر، يصبح متجه السرعة مماسًا لمسار الجسيم.

يمكن أيضًا كتابة المعادلة\ ref {4.4} من حيث مكونات$\vec{v}$ (t). منذ

\[\vec{r} (t) = x(t)\; \hat{i} + y(t)\; \hat{j} + z(t)\; \hat{k},\]

يمكننا الكتابة

\[\vec{v} (t) = v_{x} (t)\; \hat{i} + v_{y} (t)\; \hat{j} + v_{z} (t)\; \hat{k} \label{4.5}\]

حيث

\[v_{x} (t) = \frac{dx(t)}{dt}, \quad v_{y} (t) = \frac{dy(t)}{dt}, \quad v_{z} (t) = \frac{dz(t)}{dt} \ldotp \label{4.6}\]

إذا كان متوسط السرعة فقط هو مصدر القلق، فلدينا المكافئ المتجه لمتوسط السرعة أحادي البعد لبعدين وثلاثة أبعاد:

\[\vec{v}_{avg} = \frac{\vec{r} (t_{2}) - \vec{r} (t_{1})}{t_{2} - t_{1}} \ldotp \label{4.7}\]

مثال 4.3: حساب متجه السرعة

وظيفة موضع الجسيم هي$\vec{r}$ (t) = 2.0t ^{$\hat{i}$2+} (2.0 + 3.0t)$\hat{j}$ + 5.0t$\hat{k}$ m. (أ) ما هي السرعة اللحظية والسرعة عند t = 2.0 ثانية؟ (ب) ما متوسط السرعة بين 1.0 ثانية و3.0 ثانية؟

الحل

باستخدام المعادلة\ ref {4.5} والمعادلة\ ref {4.6}، وأخذ مشتق دالة الموضع فيما يتعلق بالوقت، نجد

$v (t) =\ frac {d\ vec {r} (t)} {dt} = 4.0t\؛\ قبعة {i} + 3.0\؛\ قبعة {j} + 5.0\؛\ قبعة {ك}\؛ م/s$$$\ vec {v} (2.0\؛ s) = 8.0\؛\ قبعة {i} + 3.0\؛\ قبعة {j} + 5.0\؛\ قبعة {j} + 5.0\ k}\; M/S$$$$السرعة\; |\ vec {v} (2.0\; s) | =\ sqrt {8^ {2} + 3^ {2} + 5^ {2}} = 9.9\؛ م/ث\ ldotp$$
من المعادلة\ المرجع {4.7}، $$\ ابدأ {الانقسام}\ vec {v} _ {avg} & =\ frac {\ vec {r} (t_ {2}) -\ vec {r} (t_ {1})} {t_ {2} - t_ {1} - t_ {1} =\ frac {\ r} (3.0\; s) -\ vec {r} (1.0\; S)} {3.0\; s - 1.0\; s} =\ frac {(18\;\ قبعة {i} + 11\;\ قبعة {j} + 15\;\ قبعة {k}) م - (2\;\ قبعة {i} + 5\;\ قبعة {j} + 5\;\ قبعة {k}) م} {2.0\; s}\\\\\\ فراك ( 16\;\ قبعة {i} + 6\;\ قبعة {j} + 10\;\ قبعة {k}) م} {2.0\; s} = 8.0\;\ قبعة {i} + 3.0\;\ قبعة {j} + 5.0\;\ قبعة {k}\\; م/ث\ ldotp\ end {تقسيم} $$

الدلالة

نرى أن متوسط السرعة هو نفس السرعة اللحظية عند t = 2.0 ثانية، نتيجة لكون دالة السرعة خطية. لا يجب أن يكون هذا هو الحال بشكل عام. في الواقع، في معظم الأوقات، لا تكون السرعات اللحظية والمتوسطة هي نفسها.

التمرين 4.1

دالة موضع الجسيم هي$\vec{r}$ (t) = 3.0t ^{$\hat{i}$3+} 4.0$\hat{j}$. (أ) ما السرعة اللحظية عند t = 3 ثوان؟ (ب) هل متوسط السرعة بين ثانيتين و4 ثوان يساوي السرعة اللحظية عند t = 3 ثوان؟

استقلالية الحركات العمودية

عندما ننظر إلى المعادلات ثلاثية الأبعاد للموضع والسرعة المكتوبة بترميز متجه الوحدة والمعادلة\ ref {4.2} والمعادلة\ ref {4.5}، نرى أن مكونات هذه المعادلات هي وظائف زمنية منفصلة وفريدة لا تعتمد على بعضها البعض. لا تحتوي الحركة على طول الاتجاه x على أي جزء من حركتها على طول الاتجاهين y و z، وبالمثل بالنسبة لمحوري الإحداثيات الآخرين. وبالتالي، يمكن تقسيم حركة كائن في بعدين أو ثلاثة أبعاد إلى حركات منفصلة ومستقلة على طول المحاور العمودية لنظام الإحداثيات الذي تحدث فيه الحركة.

ولتوضيح هذا المفهوم فيما يتعلق بالنزوح، فكر في امرأة تسير من النقطة A إلى النقطة B في مدينة ذات كتل مربعة. قد تسير المرأة التي تسلك المسار من A إلى B شرقًا للعديد من الكتل ثم شمالًا (اتجاهين عموديين) حتى تصل مجموعة أخرى من الكتل إلى B. ولا يتأثر مدى مشيها شرقًا إلا بحركتها شرقًا. وبالمثل، فإن المسافة التي تمشي بها شمالًا لا تتأثر إلا بحركتها شمالًا.

استقلال الحركة

في الوصف الحركي للحركة، يمكننا معالجة المكونات الأفقية والعمودية للحركة بشكل منفصل. في كثير من الحالات، لا تؤثر الحركة في الاتجاه الأفقي على الحركة في الاتجاه الرأسي والعكس صحيح.

يتم إعطاء مثال يوضح استقلالية الحركات الرأسية والأفقية بواسطة كرتي بيسبول. يتم إسقاط كرة بيسبول واحدة من الراحة. في نفس اللحظة، يتم طرح آخر أفقيًا من نفس الارتفاع ويتبع مسارًا منحنيًا. يلتقط ستروبوسكوب مواضع الكرات على فترات زمنية محددة عند سقوطها (الشكل$\PageIndex{7}$).

تم توضيح كرتين متطابقتين في 5 مواقع على فترات زمنية متساوية. تبدأ الكرات في نفس الوضع الرأسي. تمثل الأسهم الخضراء السرعات الأفقية وتمثل الأسهم الأرجوانية السرعات الرأسية في كل موضع. الكرة الموجودة على اليمين لها سرعة أفقية أولية بينما الكرة على اليسار ليس لها سرعة أفقية. الحركة الأفقية هي سرعة أفقية ثابتة في جميع الأوقات لكلتا الكرتين. الحركة الرأسية هي تسارع عمودي ثابت. تزداد السرعة الرأسية لكل كرة من حيث الحجم وتشير لأسفل. في كل لحظة زمنية، تتمتع كلتا الكرتين بأوضاع رأسية وسرعات رأسية متطابقة. — الشكل$\PageIndex{7}$: رسم تخطيطي لحركات كرتين متطابقتين: تسقط إحداهما من السكون والأخرى بسرعة أفقية أولية. كل موضع لاحق هو فترة زمنية متساوية. تمثل الأسهم السرعات الأفقية والعمودية في كل موضع. الكرة الموجودة على اليمين لها سرعة أفقية أولية بينما الكرة على اليسار ليس لها سرعة أفقية. على الرغم من الاختلاف في السرعات الأفقية، فإن السرعات والمواضع الرأسية متطابقة لكلتا الكرتين، مما يدل على أن الحركات الرأسية والأفقية مستقلة.

من اللافت للنظر أن المواضع الرأسية للكرتين هي نفسها لكل ومضة من الوميض من الوميض. يشير هذا التشابه إلى أن الحركة الرأسية مستقلة عما إذا كانت الكرة تتحرك أفقيًا. (بافتراض عدم وجود مقاومة للهواء، تتأثر الحركة الرأسية للجسم الساقط بالجاذبية فقط، وليس بأي قوى أفقية.) يُظهر الفحص الدقيق للكرة التي يتم إلقاؤها أفقيًا أنها تقطع نفس المسافة الأفقية بين الومضات. هذا بسبب عدم وجود قوى إضافية على الكرة في الاتجاه الأفقي بعد رميها. هذه النتيجة تعني أن السرعة الأفقية ثابتة ولا تتأثر بالحركة الرأسية ولا بالجاذبية (الرأسية). لاحظ أن هذه الحقيبة مناسبة للظروف المثالية فقط. في العالم الحقيقي، تؤثر مقاومة الهواء على سرعة الكرات في كلا الاتجاهين.

يتكون المسار المنحني ثنائي الأبعاد للكرة التي يتم رميها أفقيًا من حركتين مستقلتين أحادية البعد (أفقية وعمودية). مفتاح تحليل هذه الحركة، التي تسمى حركة المقذوفات، هو حلها في حركات على طول الاتجاهات العمودية. يمكن حل الحركة ثنائية الأبعاد إلى مكونات عمودية لأن المكونات مستقلة.