7.1: ميل الخط
- Last updated
- Oct 31, 2022
- Page ID
- 166918
- Save as PDF
تذكر أنه يمكن رسم الأزواج المرتبة على هيئة نقاط في المستوى الإحداثي المستطيل. من خلال أي نقطتين متميزتين، قم برسم خط مستقيم،l.
لوصف الخطl جبريًا، ضع في اعتبارك أولاً ميل الصيغة الخطية.
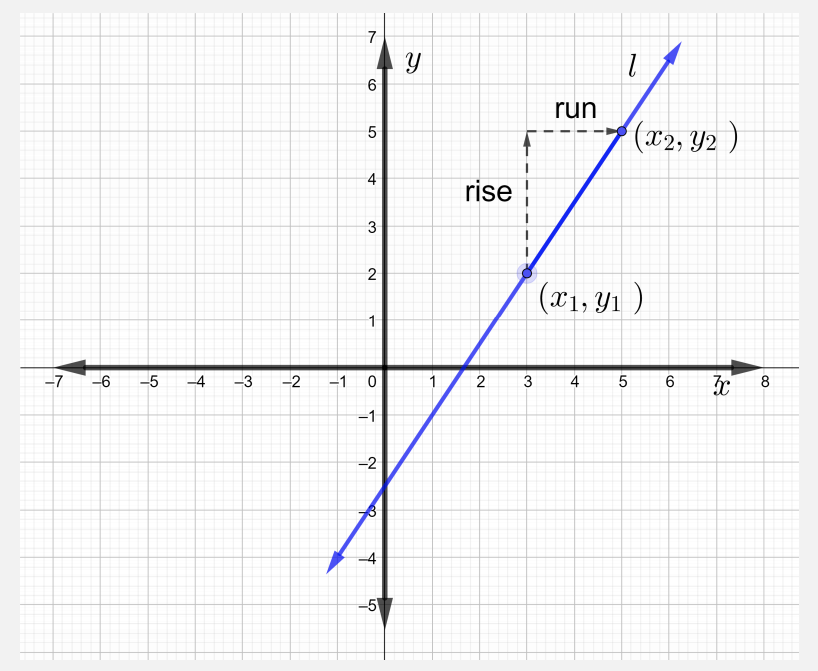
ميلm الخطl الذي يمر عبر النقاط(x1,y1)(x2,y2) وهو
m=riserun=y2−y1x2−x1 where x2≠x1
ابحث عن ميل الخط في الشكل أدناه.
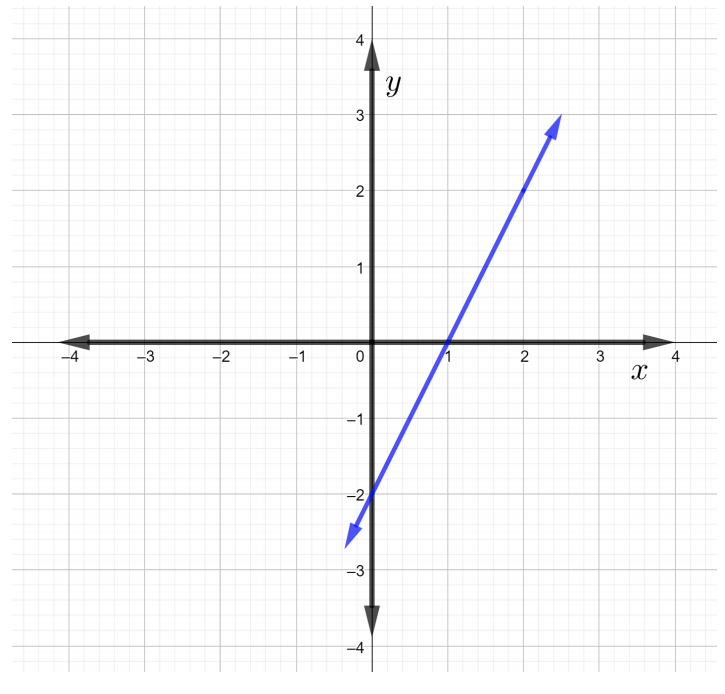
الحل
من خلال التعريف أعلاه لمنحدر صيغة الخط، يمكن كتابة منحدر الخط كـm=riserun. ابدأ باختيار أي نقطتينQ،P وعلى الخط. اختر النقطةP التي تريد أن تكون(2,2) وأشرQ إلى أن تكون(1,0).
بدءًا من النقطةQ، قم بالارتفاع حتى النقطةP عن طريق حساب مربعات2 الشبكة التصاعدية، مما يعنيrise=2. الآن، للوصول إلى النقطةP، مربعrun1 الشبكة إلى اليمين، مما يعني ذلكrun=1، كما هو موضح في الشكل أدناه.
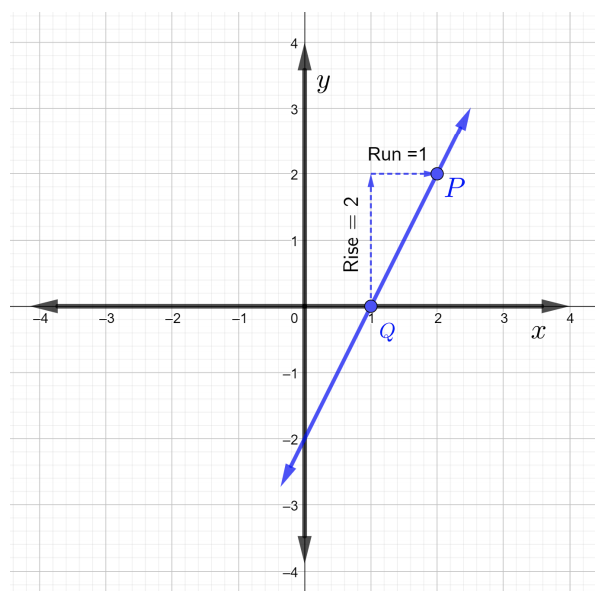
وهكذا،
\boldsymbol{\begin{array} &&m = \dfrac{\text{rise}}{\text{run}} &\text{slope of a line formula} \\ &= \dfrac{2}{1} &\text{rise \(2}وتشغيل1}\\ &= 2\ end {مصفوفة}\)
لذلك، يكون ميل الخط في الشكل هوm=2.
أوجد ميل الخط المستقيم الموضح في الشكل أدناه.
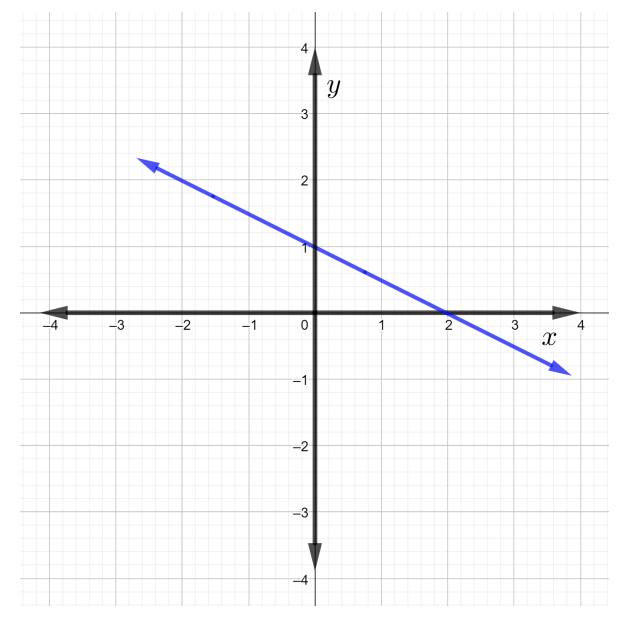
الحل
على غرار المثال1، ابدأ باختيار أي نقطتينQ،P وعلى الخط.
ملاحظة: نظرًا لأنه يمكن اختيار أي2 نقاط على السطر، سيكون من الأسهل اختيار النقطتين اللتين تمثلان أعدادًا صحيحة. توجد هذه النقاط على الخط وأيضًا عند تقاطع خطين من خطوط الشبكة. على سبيل المثال، في الشكل، سيكون من الأسهل اختيار أي نقطتين من النقاط التالية في السطر المحدد:(2,0)،،(0,1)،(4,−1)،(6,−2)(−4,3)،(−6,4)، وما إلى ذلك...
المنحدر هو نفسه لأي نقطتينPQ وعلى الخط. اختر النقطةP1 التي تريد أن تكون(0,1) وأشرQ1 إلى أن تكون(2,0). بدءًا من النقطةP1، تصل إلى النقطةQ1 عن طريق تشغيل مربعات2 الشبكة أولاً إلى اليمين، مما يعني أنrun=2. الآن، للوصول إلى مربع1 الشبكة التنازليQ1 لحساب النقاط. لاحظ أن هذاrise=−1 يعني نقل1 الوحدة لأسفل كما هو موضح في الشكل أدناه.
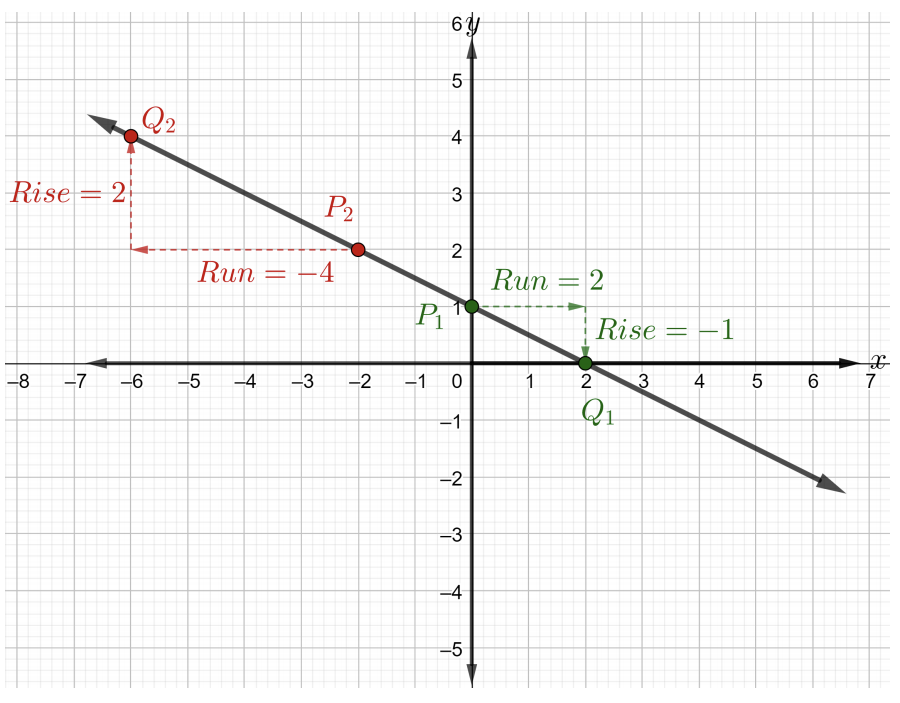
\boldsymbol{\begin{array} &&m = \dfrac{\text{rise}}{\text{run}} &\text{slope of a line formula} \\ &= \dfrac{−1}{2} &\text{rise = \(-1}وتشغيل =2}\ end {مصفوفة}\)
لذلك، فإن منحدر الخط في الشكل أعلاه هوm=−12.
الآن، اختر النقطةP2 التي تريد أن تكون(−2,2) وأشرQ2 إلى أن تكون(−6,4) كما هو موضح في الشكل أعلاه. بدءًا من النقاطP2، يمكنك الوصول إلى النقطةQ2 عن طريق تشغيل مربعات4 الشبكة أولاً إلى اليسار، مما يعني أنrun=−4. الآن، للوصول إلىQ2 عدد النقاط إلى مربعات2 الشبكة التصاعدية. وهكذا، فإنrise=2. المنحدر هوm=2−4=−12. لاحظ أن المنحدر هو نفسه بغض النظر عن2 النقاط التي نعتبرها على خط معين.
أوجد ميل الخط الذي يمر(3,2) عبره(4,4) واستخدم صيغة المنحدر. ارسم بيانيًا الخط الذي يمر بالنقاط المعطاة.
ملاحظة: لن يحدث ترتيب تسمية النقاط فرقًا في ميل الصيغة الخطية طالما كان هناك تناسق.
الحل
دعونا(x1,y1)=(3,2) وبعد(x2,y2)=(4,4) ذلك،
\boldsymbol{\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{slope of a line formula} \\ &= \dfrac{4 − 2}{4 − 3} & \\ &= \dfrac{2}{1} &\text{rise \(= 2}وتشغيل=1}\\ &= 2\\ end {مصفوفة}\)
لذلك، يكون ميل الخط الذي يمر عبر النقطتين(3,2) و(4,4) هوm=2. الخط الذي يمر عبر النقاط المحددة هو كما هو موضح في الشكل أدناه.
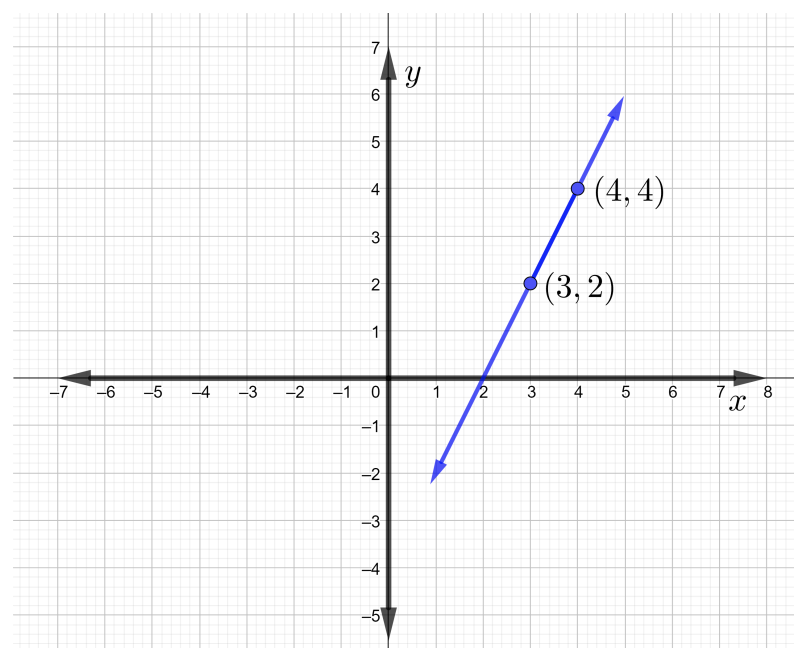
لاحظ أنه عندما يرتفع الخط من اليسار إلى اليمين، يكون للخط منحدر إيجابي.
أوجد ميل الخط الذي يمر عبر النقطتين(−1,2) و(3,−4). ارسم النقاط ورسم الخط.
الحل
دعونا(x1,y1)=(−1,2) وبعد(x2,y2)=(3,−4) ذلك،
m=y2−y1x2−x1slope of a line formula=−4−23−(−1)=−64Simplify=−32
الآن، لرسم الخط عبر النقاط المعطاة، ارسم النقطتين أولاً، ثم ارسم خطًا مستقيمًا عبرهما، كما هو موضح في الشكل أدناه.
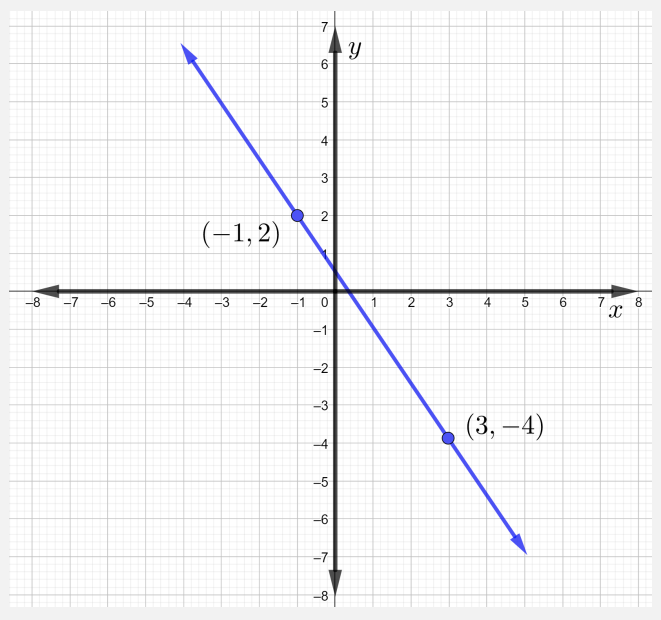
لاحظ أنه عندما يسقط الخط من اليسار إلى اليمين، يكون للخط منحدر سالب.
ابحث عن منحدرات كل سطر في الرسم البياني في حل المشكلات1 من خلال4
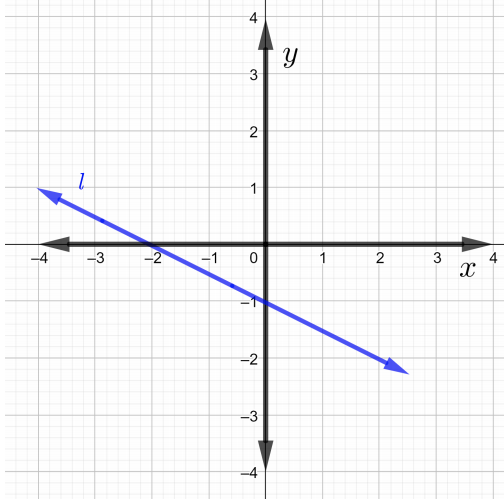
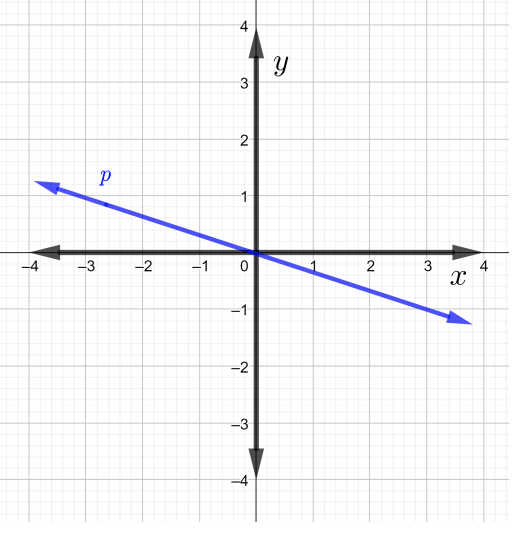
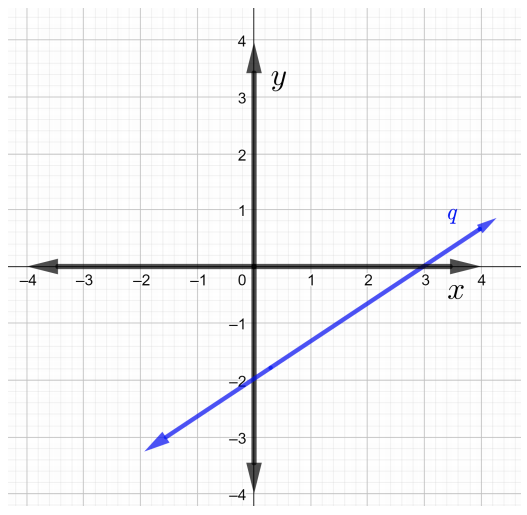
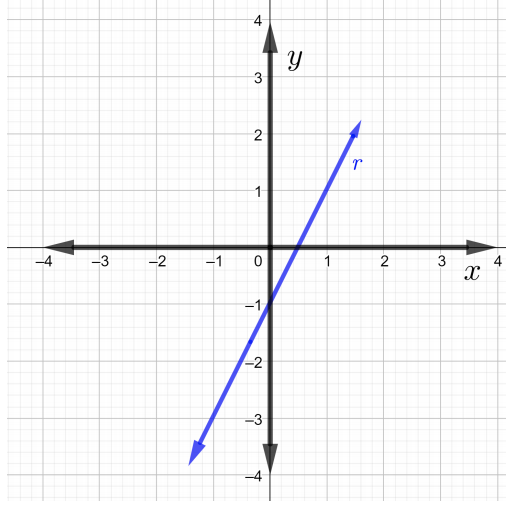
أوجد ميل الخط الذي يمر بالنقاط المُعطاة في حل المشكلات57.
- (−3,5)و(4,−5)
- (2,5)و(0,−1)
- (4,1)و(0,0)