Skip to main content
Global

2.2: أزواج مرتبة

  1. Last updated
  2. Save as PDF
  • Page ID
    167014

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    تعريف: الأزواج المرتبة

    الأزواج المرتبة هي أزواج من الأرقام المستخدمة لتحديد موقع نقطة في المستوى الإحداثي المستطيل ومكتوبة في النموذج\((x, y)\)، حيث x هو الإحداثي x و y هو الإحداثي y.

    سيحدد موقع الزوج المرتب في الأرباع علامة الإحداثيات x و y، كما هو موضح في القسم السابق، الشكل أعلاه. وبالتالي،\((x, y)\) يتم تلخيص علامات الأزواج المرتبة على النحو التالي،

    • \((x, y)\)إذا كان في الربع الأول، فسيكون كل من x و y موجبين.
    • إذا كان\((x, y)\) في الربع الثاني، فإن x يكون سالبًا و y موجبًا.
    • \((x, y)\)إذا كان في الربع الثالث، فسيكون كل من x و y سالبين.
    • \((x, y)\)إذا كان في الربع الرابع، فسيكون x موجبًا و y سالبًا.

    ملاحظة: لا تنتمي النقاط الموجودة على المحور العمودي في المستوى المستطيل إلى أي من الأرباع.

    لتحديد موقع نقطة في المستوى الإحداثي، استخدم عملية تسمى رسم نقطة بيانيًا. يمكن أيضًا تسمية هذه العملية بتخطيط نقطة. ابدأ دائمًا من نقطة الأصل وتحرك يمينًا أو يسارًا لتحديد موقع الإحداثيات x والتحرك لأعلى أو لأسفل لتحديد موقع الإحداثيات y.

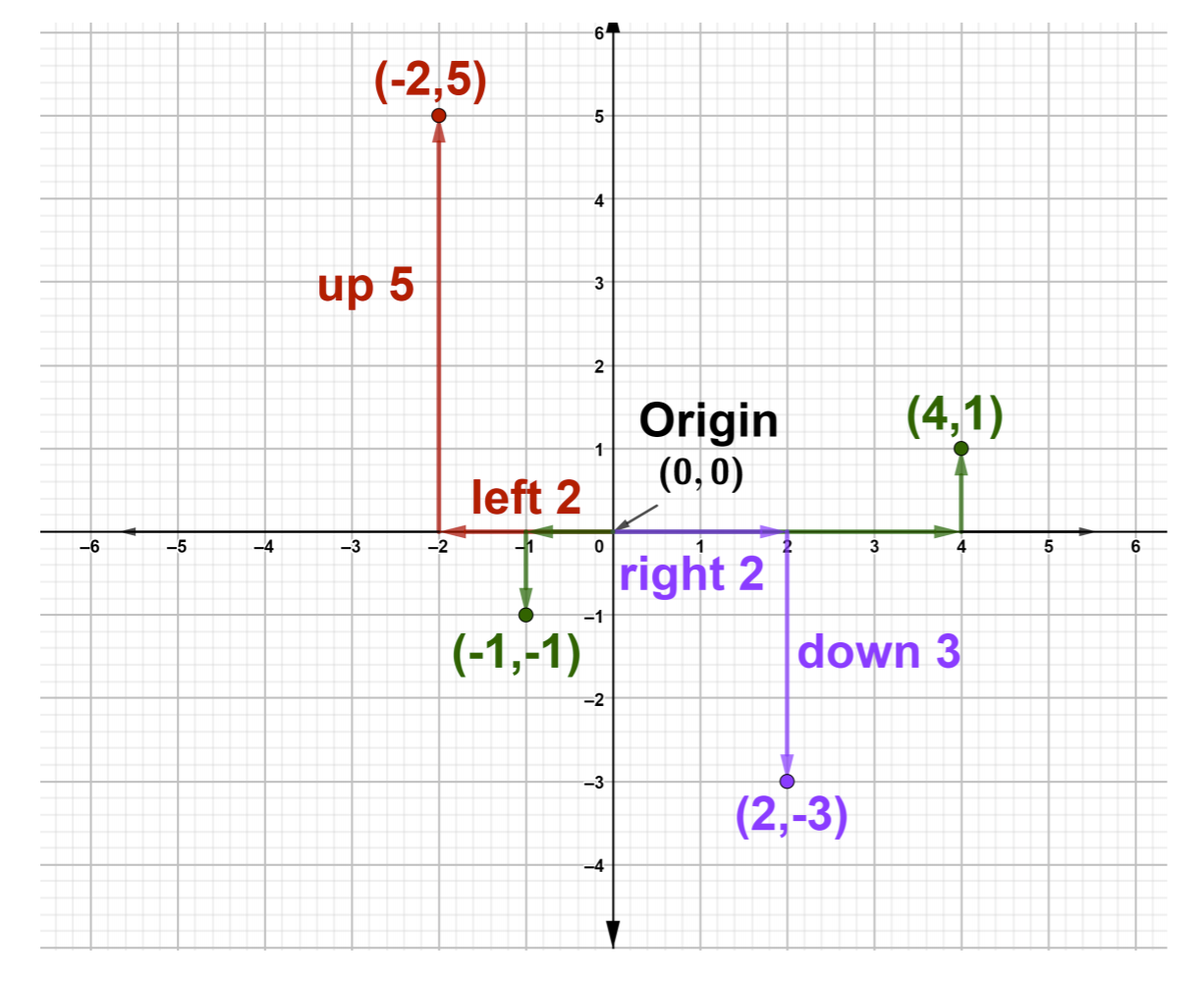
    للرسم البياني أو الرسم\((−2, 5)\) على مستوى إحداثي، ابدأ من نقطة الأصل وحرك وحدتين إلى اليسار، لأن الإحداثي السيني −2 سالب، ثم حرّك لأعلى بمقدار 5 وحدات لأن الإحداثي y 5 إيجابي وارسم نقطة. لاحظ أن نقطتنا في الربع الثاني. لرسم النقطة بيانيًا\((4, 1)\)، ابدأ من نقطة الأصل وانقل 4 وحدات إلى اليمين ووحدة واحدة لأعلى. وبالمثل، قم برسم النقاط\((2, −3)\)،\((−1, −1)\) وكما هو موضح في الشكل أدناه.

    clipboard_ecc7ea694bef846b2f27633e461fddb92.png
    الشكل
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/02:_نظام_الإحداثيات_الديكارتية/2.02:_أزواج_مرتبة), /content/body/figure/figcaption/span, line 1, column 17

    كن حذرًا! في الفصل السابق،\((p, q)\) تم استخدام الترميز لتمثيل حل عدم المساواة في القيمة المطلقة في الترميز الفاصل الزمني. يقدم هذا القسم الأزواج المرتبة التي تستخدم نفس تمثيل الأقواس. تأكد من عدم الخلط بين الترميز الفاصل الزمني ورموز الأزواج المرتبة.

    مثال
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/02:_نظام_الإحداثيات_الديكارتية/2.02:_أزواج_مرتبة), /content/body/section[2]/header/div/h5/span/span, line 1, column 17

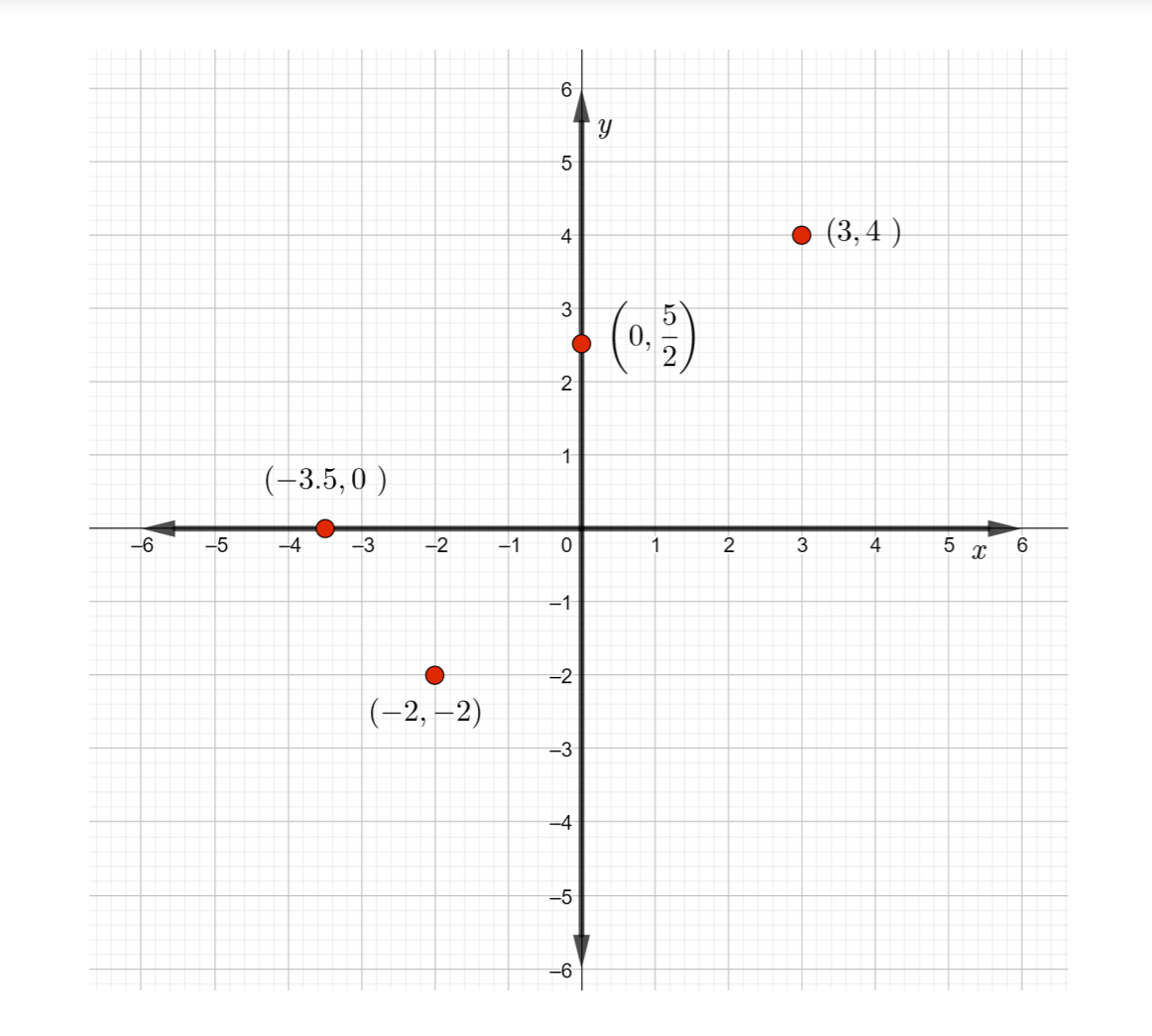
    ارسم النقاط المعطاة على نفس المستوى الإحداثي المستطيل، وحدد مكان كل نقطة. إذا كانت النقطة لا تقع في أي من الأرباع، فاذكر المحور الذي تقع عليه.

    1. \((3, 4)\)
    2. \((−2, −2)\)
    3. \(\left(0, \dfrac{5 }{2 }\right)\)
    4. \((−3.5, 0)\)
    الحل
    1. كل من إحداثيات x و y موجبة. ابدأ من نقطة\((3, 4)\) الأصل، انقل 3 وحدات إلى اليمين ثم تحرك لأعلى 4 وحدات وحدد النقطة تقع النقطة في الربع الأول
    2. كل من إحداثيات x و y سالبة. ابدأ من نقطة الأصل، وانقل وحدتين إلى اليسار، ثم انقل وحدتين لأسفل وحدد النقطة\((−2, −2)\). النقطة تكمن في الربع الثاني.
    3. بما أن الإحداثي السيني هو 0، ابدأ من نقطة الأصل ولا تتحرك يمينًا أو يسارًا. نظرًا لأن الإحداثي y إيجابي، قم بتحريك\(\dfrac{5 }{2}\) الوحدات أو 2.5 وحدة لأعلى. نقطة التسمية\(\left(0, \dfrac{5 }{2} \right)\). النقطة تقع على المحور y.
    4. عندما يكون الإحداثي السيني سالبًا، ابدأ من نقطة الأصل وانقل 3.5 وحدة إلى اليسار. نظرًا لأن الإحداثي y هو 0، فلا تتحرك لأعلى أو لأسفل. قم بتسمية النقطة\((−3.5, 0)\). النقطة تقع على المحور السيني.
    clipboard_e573613a9ab5fcefc461a9666e98d841c.png
    الشكل
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/02:_نظام_الإحداثيات_الديكارتية/2.02:_أزواج_مرتبة), /content/body/section[2]/div/figure/figcaption/span, line 1, column 17
    مثال
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/02:_نظام_الإحداثيات_الديكارتية/2.02:_أزواج_مرتبة), /content/body/section[3]/header/div/h5/span/span, line 1, column 17

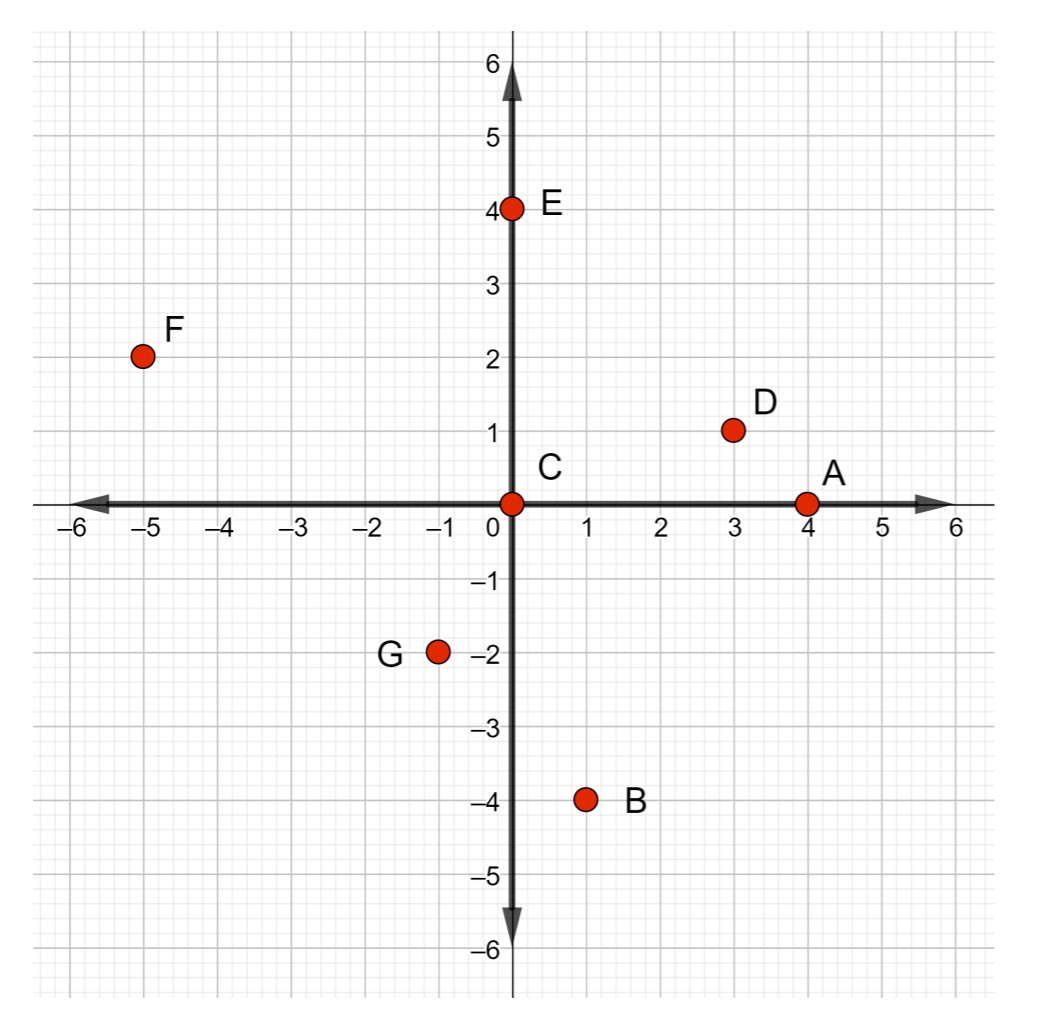
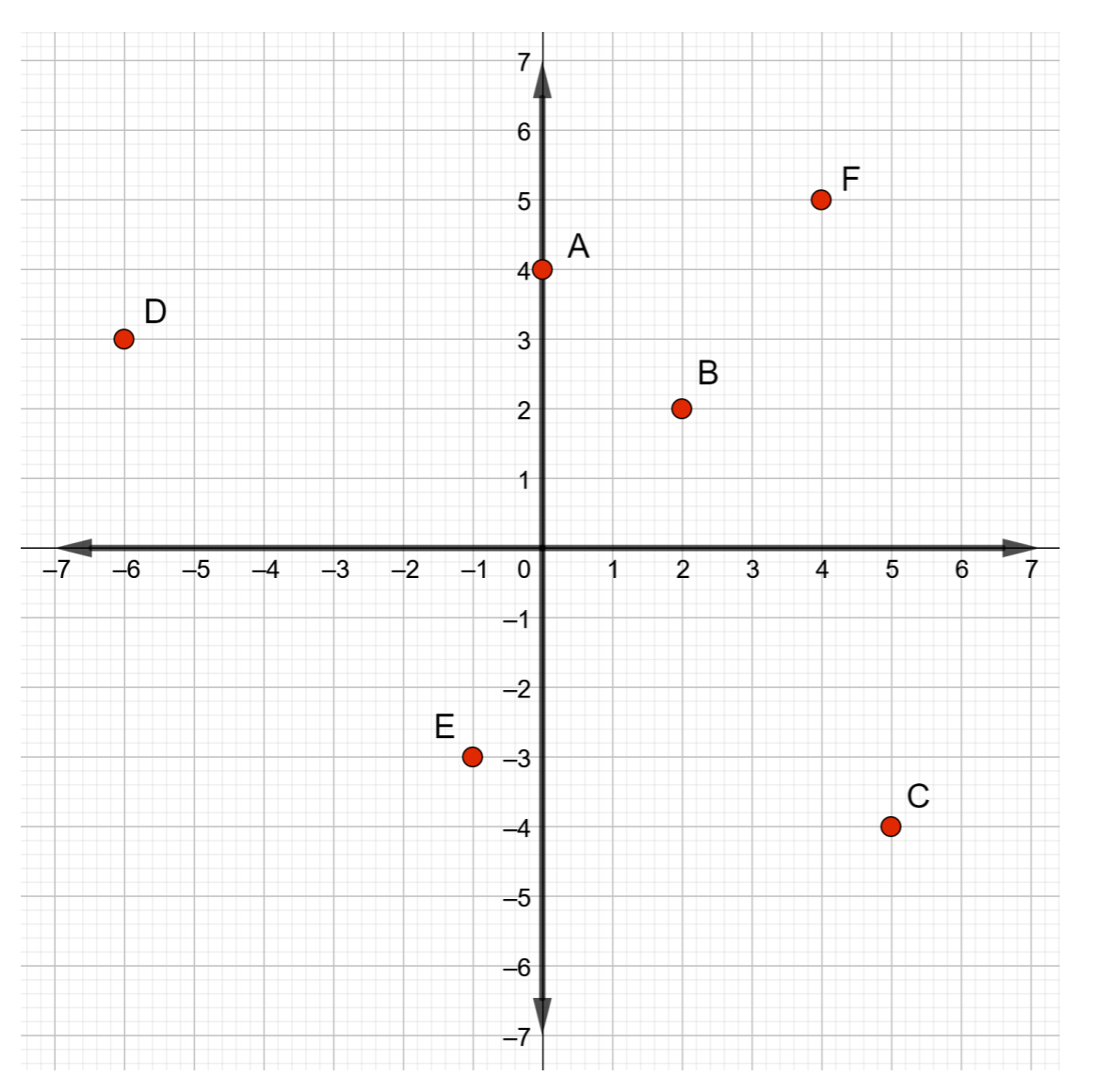
    حدد إحداثيات النقاط المسماة في الشكل أدناه.

    clipboard_e82d2ac1b4e4fd23029801b11c2f8673e.png
    الشكل
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/02:_نظام_الإحداثيات_الديكارتية/2.02:_أزواج_مرتبة), /content/body/section[3]/figure/figcaption/span, line 1, column 17
    الحل

    لرسم أي نقطة في المستوى الإحداثي، ابدأ من نقطة الأصل ثم تحرك وفقًا لعلامة الإحداثيات المعطاة على النحو التالي،

    • النقطة A: ابدأ من الأصل وانقل 4 وحدات إلى اليمين. الإحداثي السيني هو 4. لا توجد حركة رأسية لأعلى أو لأسفل، لذا فإن الإحداثي y هو 0. وبالتالي، تحتوي النقطة A على إحداثيات\((4, 0)\)
    • النقطة B: مرة أخرى، ابدأ من نقطة الأصل وانقل وحدة واحدة إلى اليمين و 4 وحدات لأسفل. وبالتالي، تحتوي النقطة B على إحداثيات\((1, −4)\)
    • النقطة C: نظرًا لأن الإحداثي x هو 0، فابدأ من نقطة الأصل ولا تتحرك يمينًا أو يسارًا. الإحداثي y هو 0 أيضًا، لذا لا تتحرك لأعلى أو لأسفل. وبالتالي، فإن إحداثيات النقطة C هي\((0, 0)\)
    • النقطة D: من الأصل، انقل 3 وحدات إلى اليمين، ثم وحدة واحدة لأعلى. وبالتالي، فإن إحداثيات النقطة D هي\((3, 1)\)
    • النقطة E: ابدأ من نقطة الأصل وابق هناك لأن الإحداثي x هو 0، ثم انقل 4 وحدات لأعلى. وبالتالي، تحتوي النقطة E على إحداثيات\((0, 4)\).
    • النقطة F: انقل 5 وحدات إلى اليسار من الأصل ووحدتين لأعلى. تحتوي النقطة F على إحداثيات\((−5, 2)\)
    • النقطة G: انقل وحدة واحدة إلى اليسار من الأصل ووحدتين لأسفل. تحتوي النقطة G على إحداثيات\((−1, −2)\)
    التمرين
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/02:_نظام_الإحداثيات_الديكارتية/2.02:_أزواج_مرتبة), /content/body/section[4]/header/div/h5/span/span, line 1, column 17
    1. ما هي إحداثيات x و y في\((−3, 2)\) و\((2, −3)\)؟ هل هما نفس النقطة؟
    2. ارسم النقاط التالية على نفس المستوى الإحداثي المستطيل، وحدد الربع الذي تقع فيه كل نقطة أو المحور الذي تقع عليه. \((−1.5, 2),\quad (0, −3), \quad(5, 2.5),\quad \left(− \dfrac{1}{ 2 },\quad − \dfrac{1 }{2}\right), \quad\left(3\dfrac{1 }{2} ,\quad −\dfrac{ 7 }{2}\right ), \quad (−3, 3),\quad (−2, 0)\)
    3. حدد إحداثيات كل نقطة معينة في الشكل أدناه.
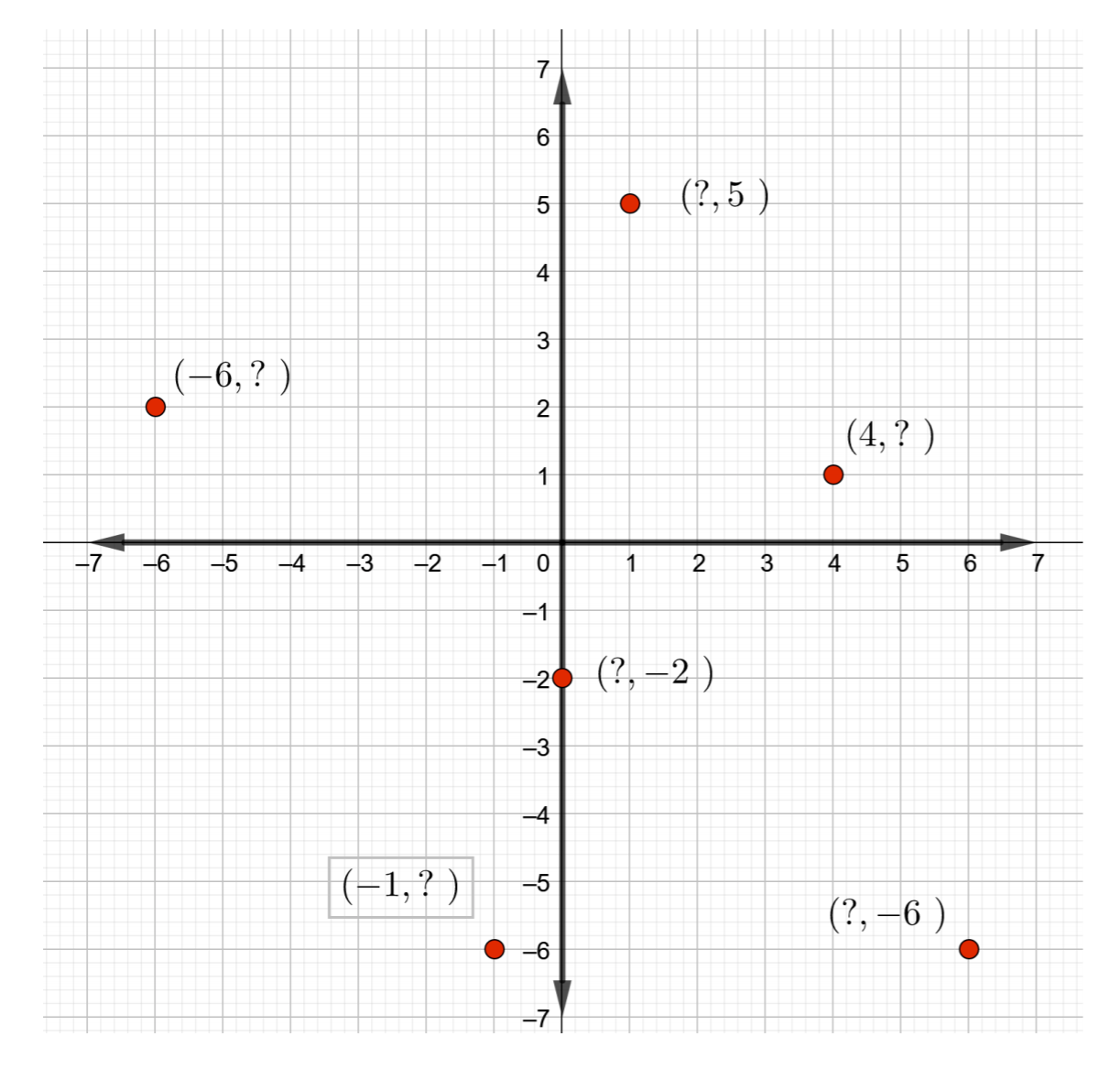
      clipboard_e1ef80ad5824aad92f10d741b80deac84.png
      الشكل
      ParseError: invalid ArgList (click for details)
      Callstack:
    at (اللغة_العربية/(__)/02:_نظام_الإحداثيات_الديكارتية/2.02:_أزواج_مرتبة), /content/body/section[4]/ol/li[3]/figure/figcaption/span, line 1, column 17
    4. حدد إحداثيات كل نقطة معينة في الشكل أدناه.
      clipboard_ef393b7a664660f0ac9517c9066d7f940.png
      الشكل
      ParseError: invalid ArgList (click for details)
      Callstack:
    at (اللغة_العربية/(__)/02:_نظام_الإحداثيات_الديكارتية/2.02:_أزواج_مرتبة), /content/body/section[4]/ol/li[4]/figure/figcaption/span, line 1, column 17