2.1: أرباع التعريف والتسمية

Last updated
Save as PDF

Page ID: 167013

Victoria Dominguez, Cristian Martinez, & Sanaa Saykali
Citrus College via ASCCC Open Educational Resources Initiative

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

تعريف: نظام الإحداثيات المستطيلة

يُعرف نظام الإحداثيات المستطيلة أيضًا باسم نظام الإحداثيات الديكارتية، وهو يعتمد على شبكة ويتكون من خطين عموديين، خط الأعداد الأفقي الذي يسمى المحور السيني وخط الأعداد العمودي الذي يسمى المحور y. يمكن تحديد كل نقطة في نظام الإحداثيات المستطيلة من خلال إحداثيات x و y الفريدة.

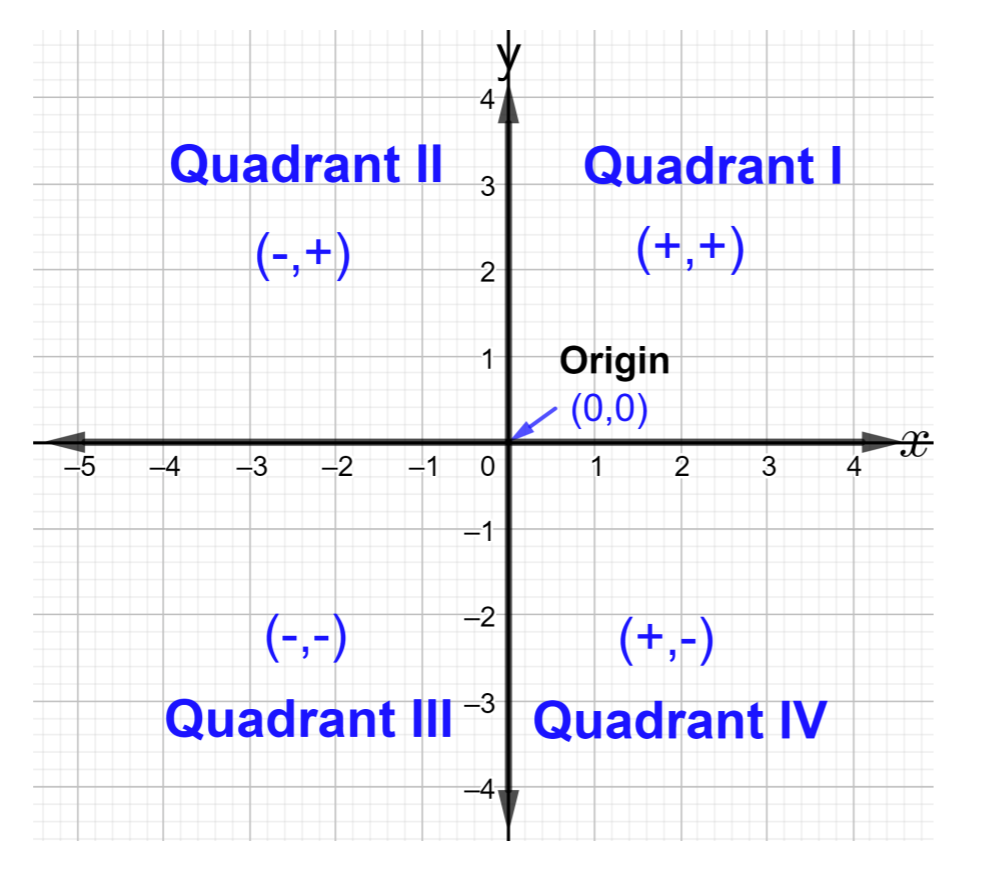
يتقاطع خطان الأرقام المتعامدان عند النقطة\((0, 0)\) ويُطلق عليهما اسم الأصل. ينقسم نظام الإحداثيات المستطيلة إلى أربع مناطق. تُسمى المناطق الأرباع وتُصنف بالأرقام الرومانية على النحو التالي: الربع الأول والربع الثاني والربع الثالث والربع الرابع، كما هو موضح في الشكل أدناه

الشكل
ParseError: invalid ArgList (click for details)
Callstack: at (اللغة_العربية/(__)/02:_نظام_الإحداثيات_الديكارتية/2.01:_أرباع_التعريف_والتسمية), /content/body/figure/figcaption/span, line 1, column 17

تتوافق كل نقطة في المستوى الإحداثي مع زوج مرتب فريد\((x, y)\)، أين\(x\)\(y\) توجد أي أرقام حقيقية. يحتوي الزوج الذي تم ترتيبه دائمًا على الإحداثي السيني الأول (على اليسار) والثاني\(y\) الإحداثي (على اليمين). \((6, 4)\)،\(\left(−.33, \dfrac{1}{5} \right)\)،\((100, −2)\)،\(\left( \sqrt{ 3}, \dfrac{1 }{2}\right )\) هي أمثلة قليلة على الأزواج المرتبة. اقرأ الزوج\((6, 4)\) المُرتب كـ «النقطة ستة، أربعة» حيث 6 هي\(x\) الإحداثيات -و 4 هي\(y\) الإحداثيات -.

التمرين

ParseError: invalid ArgList (click for details)

Callstack:
    at (اللغة_العربية/(__)/02:_نظام_الإحداثيات_الديكارتية/2.01:_أرباع_التعريف_والتسمية), /content/body/section[2]/header/div/h5/span/span, line 1, column 17

ما هي النقاط التي تسمى في النموذج\((x, y)\)؟
حدد إحداثيات الأزواج المرتبة التالية:\((−10, 0)\)،\((0.5, −6)\)،\(\left(\dfrac{1}{ 2} , −\dfrac{ 5 }{3} \right)\)
قم بتسمية وتحديد الزوج المرتب للنقطة التي تتقاطع فيها المحاور العمودية لنظام الإحداثيات المستطيلة.
اذكر المناطق الأربع في نظام الإحداثيات المستطيلة.
قم بتسمية الإحداثيات الأولى في زوج مرتب.
قم بتسمية الإحداثيات الثانية في زوج مرتب.
ما خط الأعداد الأفقي في نظام الإحداثيات المستطيلة؟
ما خط الأعداد العمودي في نظام الإحداثيات المستطيلة؟