3.2: احسب نقطة التعادل بالوحدات والدولار

Last updated
Save as PDF

Page ID: 190883

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

في اللبنات الأساسية للمحاسبة الإدارية، تعلمت كيفية تحديد المكونات الثابتة والمتغيرة للتكاليف والتعرف عليها، والآن تعرفت على هامش المساهمة. يمكن استخدام هذه المفاهيم معًا لإجراء تحليل التكلفة والحجم والربح (CVP)، وهي طريقة تستخدمها الشركات لتحديد ما سيحدث ماليًا في حالة تغير أسعار البيع أو تغيير التكاليف (سواء كانت ثابتة أو متغيرة) أو تغييرات في حجم المبيعات/الإنتاج.

من المهم أولاً وضع العديد من الافتراضات حول العمليات من أجل فهم تحليل CVP وبيان دخل هامش المساهمة المرتبط به. ومع ذلك، في حين أن الافتراضات التالية نموذجية في تحليل CVP، يمكن أن تكون هناك استثناءات. على سبيل المثال، بينما نفترض عادةً أن سعر البيع سيظل كما هو، فقد تكون هناك استثناءات حيث قد يُسمح بخصم الكمية. سيعتمد تحليل CVP الخاص بنا على هذه الافتراضات:

التكاليف خطية ويمكن تحديدها بوضوح على أنها ثابتة أو متغيرة. بمعنى آخر، تظل التكاليف الثابتة ثابتة بشكل إجمالي على النطاق ذي الصلة وتظل التكاليف المتغيرة ثابتة على أساس كل وحدة. على سبيل المثال، إذا كانت الشركة لديها القدرة على إنتاج ما يصل إلى$1,000$ وحدات شهريًا من المنتج نظرًا لمواردها الحالية، فسيكون$0$ النطاق المناسب هو$1,000$. إذا قرروا أنهم يريدون إنتاج$1,800$ وحدات شهريًا، فسيتعين عليهم تأمين قدرة إنتاجية إضافية. في حين أنها قد تكون قادرة على إضافة نوبة إنتاج إضافية ثم إنتاج$1,800$ وحدات شهريًا دون شراء آلة إضافية من شأنها زيادة الطاقة الإنتاجية$2,000$ للوحدات شهريًا، غالبًا ما تضطر الشركات إلى شراء معدات إنتاج إضافية لزيادة نطاقها ذي الصلة. في هذا المثال،$2,000$ ستكون القدرة الإنتاجية$1,800$ بين البلدين مصروفًا لن يوفر حاليًا مساهمة إضافية في التكاليف الثابتة.
يظل سعر البيع لكل وحدة ثابتًا ولا يزيد أو ينقص بناءً على الحجم (أي، لا يتم منح العملاء خصومات بناءً على الكمية المشتراة).
في حالة شركات التصنيع، لا يتغير المخزون لأننا نفترض أن جميع الوحدات المنتجة تباع.
في حالة الشركة التي تبيع منتجات متعددة، يظل مزيج المبيعات ثابتًا. على سبيل المثال، إذا كنا موردًا للمشروبات، فقد نفترض أن مبيعات المشروبات لدينا هي$3$ وحدات من كبسولات القهوة ووحدتين من أكياس الشاي.

باستخدام هذه الافتراضات، يمكننا أن نبدأ مناقشتنا لتحليل CVP بنقطة التعادل.

أساسيات نقطة التعادل

نقطة التعادل هي المبلغ بالدولار (إجمالي دولارات المبيعات) أو مستوى الإنتاج (إجمالي الوحدات المنتجة) الذي استعادت فيه الشركة جميع التكاليف المتغيرة والثابتة. بمعنى آخر، لا يحدث أي ربح أو خسارة عند نقطة التعادل لأن التكلفة الإجمالية = إجمالي الإيرادات. $\PageIndex{1}$يوضح الشكل مكونات نقطة التعادل:

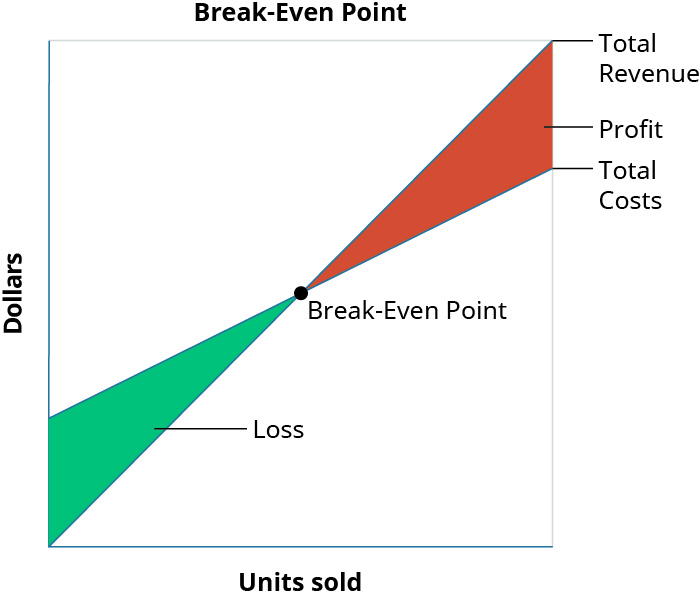
رسم بياني لنقطة التعادل حيث «الدولارات» هي المحور y و «الوحدات المباعة» هي المحور x. ينتقل السطر من الأصل إلى اليمين ويُسمى «إجمالي الإيرادات». يرتفع سطر آخر يحمل عنوان «إجمالي التكاليف» إلى الأعلى وإلى اليمين، بدءًا من المحور y فوق نقطة الأصل ولا يكون حادًا مثل السطر الأول. هناك نقطة يتقاطع فيها الخطان باسم «Break-Even Point». يتم تلوين المسافة بين السطور الموجودة على يسار تلك النقطة وتمييزها بـ «الخسارة». يتم تلوين المسافة بين السطور الموجودة على يمين تلك النقطة وتمييزها بـ «الربح». — الشكل$\PageIndex{1}$: نقطة التعادل. (الإسناد: حقوق الطبع والنشر لجامعة رايس، أوبن ستاإكس، بموجب ترخيص CC BY-NC-SA 4.0)

النظرية الأساسية الموضحة في الشكل$\PageIndex{1}$ هي أنه بسبب وجود تكاليف ثابتة في معظم عمليات الإنتاج، في المراحل الأولى من الإنتاج والبيع اللاحق للمنتجات، ستحقق الشركة خسارة. على سبيل المثال، افترض أنه في الحالة القصوى، تكون الشركة لديها تكاليف ثابتة تبلغ$\$20,000$، وسعر بيع$\$400$ لكل وحدة وتكاليف متغيرة$\$250$ لكل وحدة، ولا تبيع أي وحدات. وستحقق خسارة$\$20,000$ (التكاليف الثابتة) لأنها لم تعترف بأي إيرادات أو تكاليف متغيرة. توضح هذه الخسارة سبب اعتراف الرسم البياني لتكاليف الشركة بالتكاليف (في هذا المثال$\$20,000$) على الرغم من عدم وجود مبيعات. إذا قامت الشركة ببيع الوحدات لاحقًا، فسيتم تخفيض الخسارة بمقدار$\$150$ (هامش المساهمة) لكل وحدة يتم بيعها. وستستمر هذه العلاقة حتى نصل إلى نقطة التعادل، حيث يساوي إجمالي الإيرادات التكاليف الإجمالية. بمجرد وصولنا إلى نقطة التعادل لكل وحدة يتم بيعها، ستحقق الشركة زيادة في الأرباح بمقدار$\$150$.

بالنسبة لكل وحدة إضافية يتم بيعها، يتم تقليل الخسارة عادةً حتى تصل إلى نقطة التعادل. في هذه المرحلة، لا تحقق الشركة نظريًا أي ربح أو خسارة. بعد البيع التالي بعد نقطة التعادل، ستبدأ الشركة في تحقيق الربح، وسيستمر الربح في الزيادة مع بيع المزيد من الوحدات. في حين أن هناك استثناءات ومضاعفات يمكن دمجها، إلا أن هذه هي الإرشادات العامة لتحليل التعادل.

كما يمكنك أن تتخيل، ينطبق مفهوم نقطة التعادل على كل مسعى تجاري - التصنيع والبيع بالتجزئة والخدمة. نظرًا لتطبيقه الشامل، فهو مفهوم مهم للمديرين وأصحاب الأعمال والمحاسبين. عندما تبدأ الشركة لأول مرة، من المهم أن يعرف المالكون متى ستكون مبيعاتهم كافية لتغطية جميع تكاليفهم الثابتة والبدء في تحقيق ربح للشركة. قد تنظر الشركات الكبيرة إلى نقطة التعادل عند الاستثمار في الآلات أو المصانع أو المعدات الجديدة من أجل التنبؤ بالوقت الذي سيستغرقه حجم مبيعاتها لتغطية التكاليف الثابتة الجديدة أو الإضافية. نظرًا لأن نقطة التعادل تمثل تلك النقطة حيث لا تخسر الشركة ولا تجني المال، يحتاج المديرون إلى اتخاذ قرارات تساعد الشركة على الوصول إلى هذه النقطة وتجاوزها في أسرع وقت ممكن. لا يمكن لأي شركة أن تعمل لفترة طويلة جدًا دون مستوى التعادل. في نهاية المطاف، ستعاني الشركة من خسائر كبيرة لدرجة أنها ستضطر إلى إغلاق أبوابها.

الاعتبارات الأخلاقية: تحليل التعادل والربحية

تتمثل الخطوة الأولى في تحديد جدوى قرار العمل ببيع منتج أو تقديم خدمة في تحليل التكلفة الحقيقية للمنتج أو الخدمة والجدول الزمني للدفع للمنتج أو الخدمة. يحتاج المديرون الأخلاقيون إلى تقدير تكلفة المنتج أو الخدمة وتدفقات الإيرادات ذات الصلة لتقييم فرصة الوصول إلى نقطة التعادل.

يتطلب تحديد سعر دقيق لمنتج أو خدمة تحليلاً مفصلاً لكل من التكلفة وكيفية تغير التكلفة مع زيادة الحجم. يتضمن هذا التحليل توقيت كل من التكاليف وإيصالات الدفع، وكذلك كيفية تمويل هذه التكاليف. ومن الأمثلة على ذلك عقد خدمة تكنولوجيا المعلومات لشركة حيث سيتم تحميل التكاليف مسبقًا. عندما يتم تحميل التكاليف أو الأنشطة في البداية، تحدث نسبة أكبر من التكاليف أو الأنشطة في مرحلة مبكرة من المشروع. عادةً ما يكون عقد خدمة تكنولوجيا المعلومات مكلفًا للموظفين ويتطلب تقديرًا$120$ لأيام على الأقل من تكاليف الموظفين قبل استلام الدفعة مقابل التكاليف المتكبدة. سيتطلب عقد خدمة تكنولوجيا المعلومات للخدمات الشهرية بهامش$30\%$ ربح$4$ شهورًا من التمويل المسبق$\$280,000$ المتوازن على مدى الأشهر الأربعة قبل استلام دفعة واحدة.$\$100,000$

يتطلب الربح الإجمالي في وقت محدد تحديدًا دقيقًا لجميع التكاليف المرتبطة بإنشاء المنتج وبيعه أو تقديم الخدمة. سيقدم المحاسب الإداري الأخلاقي تقديرًا واقعيًا للتكلفة، بغض النظر عن رغبة الإدارة في بيع منتج أو تقديم خدمة. ما قد يكون منتجًا مربحًا على وجهه يحتاج إلى تحليل إضافي يقدمه المحاسب الإداري.

لتوضيح مفهوم التعادل، سنعود إلى شركة Hicks Manufacturing ونلقي نظرة على حوض طيور Blue Jay الذي يصنعونه ويبيعونه.

رابط التعلم

شاهد هذا الفيديو لمثال لأداء الخطوات الأولى لتحليل التكلفة والحجم والربح لمعرفة المزيد.

المبيعات حيث يوجد دخل التشغيل$\$0$

تهتم شركة Hicks Manufacturing بمعرفة النقطة التي يقومون فيها حتى ببيع حوض الطيور الخاص بهم من طراز Blue Jay Model. سوف تنكسر حتى عندما يكون الدخل التشغيلي$\$0$. يتم تحديد دخل التشغيل عن طريق طرح إجمالي التكاليف المتغيرة والثابتة من إيرادات المبيعات الناتجة عن المؤسسة. بعبارة أخرى، يرغب المديرون في Hicks في معرفة عدد أحواض طيور Blue Jay التي سيحتاجون إلى بيعها من أجل تغطية نفقاتهم الثابتة وتحقيق التعادل. المعلومات الخاصة بهذا المنتج هي:

الشكل 3.2.jpg — الشكل$\PageIndex{2}$: معلومات عن نموذج بلو جاي لشركة هيكس للتصنيع لشهر ديسمبر 2019

من أجل العثور على نقطة التعادل، سنستخدم هامش المساهمة لـ Blue Jay ونحدد عدد هوامش المساهمة التي نحتاجها لتغطية النفقات الثابتة، كما هو موضح أدناه.

\[\text { Break-Even Point in Units: } \dfrac{\text { Total Fixed Costs }}{\text { Contribution Margin per Unit }}\]

تطبيق هذا على هيكس يحسب على النحو التالي:

\[\dfrac{$18,000}{$80}=225\ \text { units} \nonumber\]

ما يخبرنا به هذا هو أنه يجب على هيكس بيع حمامات الطيور$225$ Blue Jay Model من أجل تغطية نفقاتها الثابتة. بمعنى آخر، لن يبدأوا في إظهار الربح حتى يبيعوا$226^{th}$ الوحدة. ويتضح ذلك في بيان دخل هامش المساهمة الخاص بهم.

الشكل 3.2.3.jpg — الشكل$\PageIndex{3}$: بيان هامش مساهمة نموذج بلو جاي لشركة هيكس للتصنيع

تظهر نقطة التعادل لشركة Hicks Manufacturing بحجم مبيعات$\$22,500$ ($225$وحدات) بيانياً في الشكل$\PageIndex{4}$.

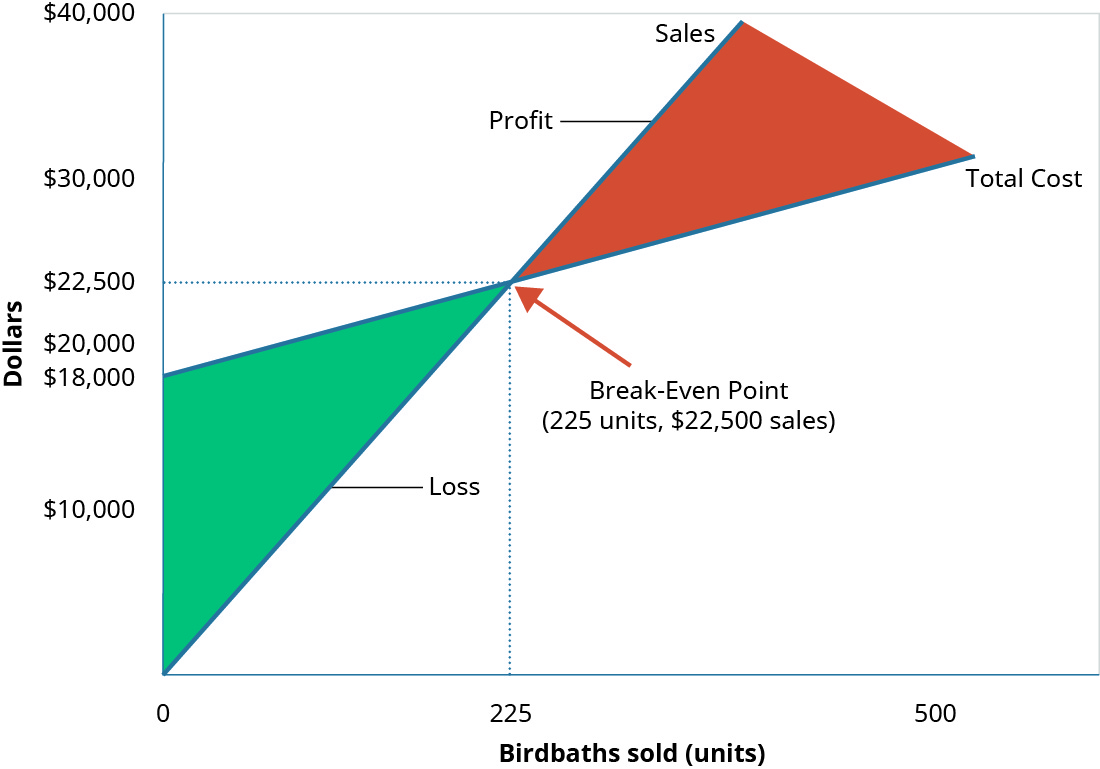
رسم بياني لنقطة التعادل حيث «الدولارات» هي المحور y و «حمامات الطيور المباعة» هي المحور x. ينتقل الخط من الأصل إلى الأعلى وإلى اليمين ويُسمى «المبيعات». يرتفع خط آخر يمثل «إجمالي التكاليف» صعودًا وإلى اليمين، بدءًا من المحور y بسعر 18000 دولار وليس حادًا مثل الخط الأول. هناك نقطة يتقاطع فيها الخطان باسم «Break-Even Point». توجد خطوط منقطة تسير بزوايا قائمة من نقطة التعادل إلى كلا المحورين، مما يوضح أن الوحدات المباعة هي 225 وحدة والتكلفة هي 22,500 دولار. يتم تلوين المسافة بين السطور الموجودة على يسار تلك النقطة وتمييزها بـ «الخسارة». يتم تلوين المسافة بين السطور الموجودة على يمين تلك النقطة وتمييزها بـ «الربح». — الشكل$\PageIndex{4}$: نقطة التعادل في تصنيع هيكس$225$ للوحدات. (الإسناد: حقوق الطبع والنشر لجامعة رايس، أوبن ستاإكس، بموجب ترخيص CC BY-NC-SA 4.0)

كما ترى، عندما تبيع هيكس أحواض الطيور من طراز$225$ Blue Jay Model، فإنها لن تحقق أي ربح، ولكنها لن تتكبد أي خسارة لأن جميع نفقاتها الثابتة مغطاة. ومع ذلك، ماذا يحدث عندما لا يبيعون$225$ الوحدات؟ إذا حدث ذلك، فإن دخل التشغيل الخاص بهم سلبي.

المبيعات حيث يكون الدخل التشغيلي سلبيًا

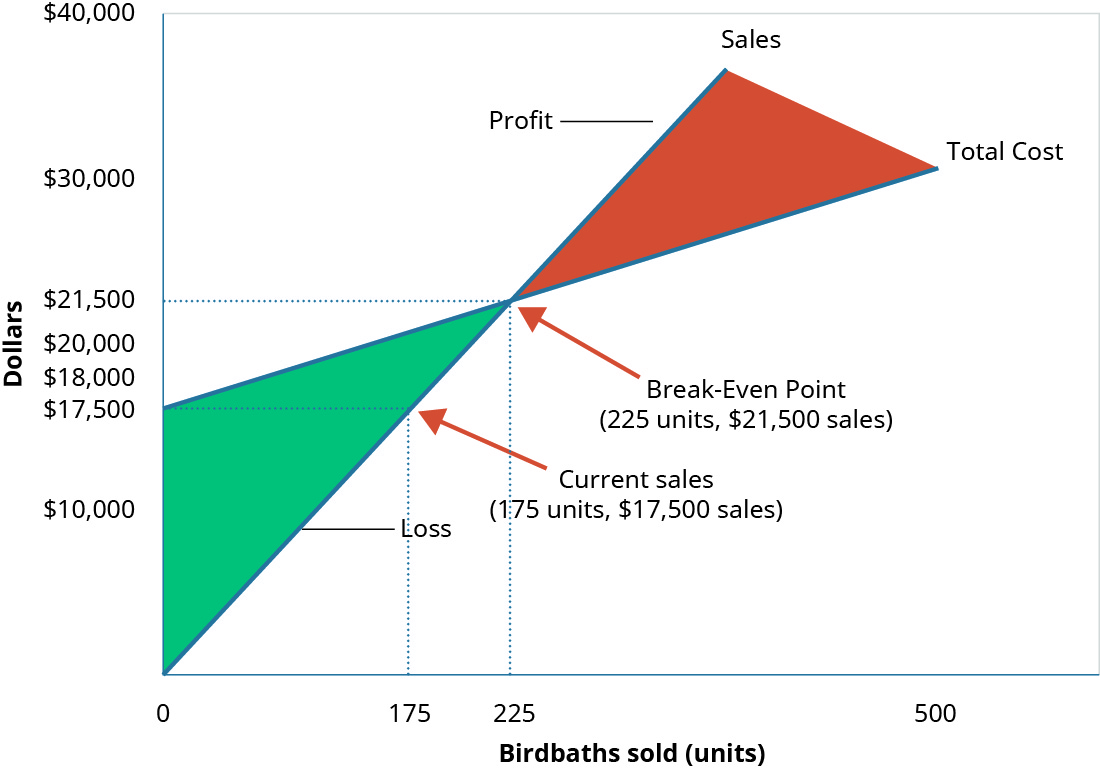
في الشهر الأخير، تسببت الفيضانات المحلية في إغلاق Hicks لعدة أيام، مما قلل من عدد الوحدات التي يمكنهم شحنها وبيعها من$225$ وحدات إلى$175$ وحدات. $\PageIndex{5}$تعكس المعلومات الواردة في الشكل هذا الانخفاض في المبيعات.

بيان دخل هامش مساهمة Hicks في التصنيع: المبيعات (175 وحدة بسعر 100 دولار لكل وحدة) 17,500 دولار ناقصًا التكلفة المتغيرة (175 وحدة بسعر 20 دولارًا لكل وحدة) 3500 يساوي هامش المساهمة 14000. اطرح التكاليف الثابتة 18,000 يساوي الدخل التشغيلي البالغ 4,000 دولار. — الشكل$\PageIndex{5}$: بيان دخل هامش مساهمة Hicks في التصنيع. (الإسناد: حقوق الطبع والنشر لجامعة رايس، أوبن ستاإكس، بموجب ترخيص CC BY-NC-SA 4.0)

في$175$ الوحدات ($\$17,500$في المبيعات)، لا تحقق Hicks إيرادات مبيعات كافية لتغطية نفقاتها الثابتة وتتعرض لخسارة$\$4,000$. لم يصلوا إلى نقطة التعادل$225$ للوحدات.

المبيعات حيث يكون الدخل التشغيلي إيجابيًا

ماذا يحدث عندما يقضي هيكس شهرًا مزدحمًا ويبيع حمامات طيور$300$ بلو جاي? لقد أثبتنا بالفعل أن هامش المساهمة من$225$ الوحدات سيضعها في وضع التعادل. عندما تتجاوز المبيعات نقطة التعادل، فإن هامش مساهمة الوحدة من الوحدات الإضافية سيتجه نحو الربح. ينعكس هذا في بيان الدخل الخاص بهم.

الشكل 3.2.7.jpg — الشكل$\PageIndex{7}$: بيان دخل هامش مساهمة Hicks في التصنيع. (الإسناد: حقوق الطبع والنشر لجامعة رايس، أوبن ستاإكس، بموجب ترخيص CC BY-NC-SA 4.0)

مرة أخرى، بالنظر إلى الرسم البياني لتحقيق التعادل (الشكل$\PageIndex{8}$)، سترى أن مبيعاتها قد تجاوزتها النقطة التي يكون فيها إجمالي الإيرادات مساويًا للتكلفة الإجمالية وإلى منطقة الربح في الرسم البياني.

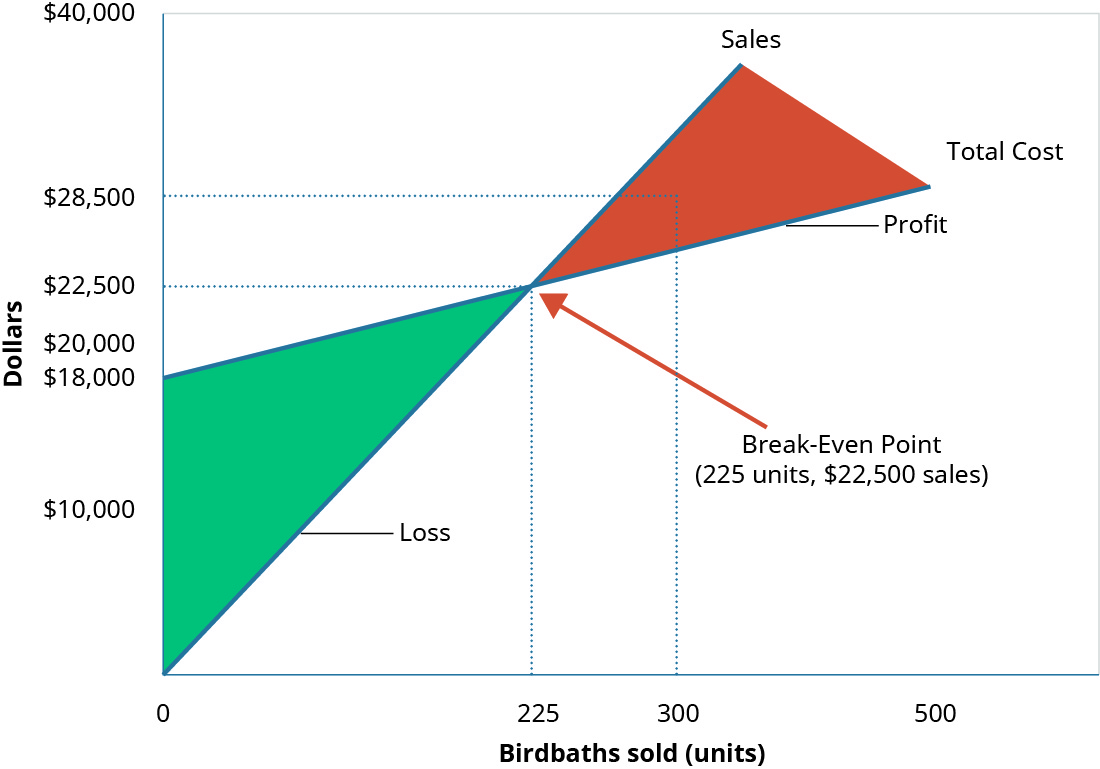
يمكن لـ Hicks Manufacturing استخدام المعلومات من هذه السيناريوهات المختلفة لإبلاغ العديد من قراراتها بشأن العمليات، مثل أهداف المبيعات.

ومع ذلك، فإن استخدام هامش المساهمة لكل وحدة ليس الطريقة الوحيدة لتحديد نقطة التعادل. تذكر أننا تمكنا من تحديد هامش المساهمة المعبر عنه بالدولار من خلال إيجاد نسبة هامش المساهمة. يمكننا تطبيق نسبة هامش المساهمة هذه على تحليل التعادل لتحديد نقطة التعادل بالدولار. على سبيل المثال، نعلم أن$\$18,000$ Hicks لديها تكاليف ثابتة ونسبة هامش$80\%$ مساهمة لنموذج Blue Jay. سنستخدم هذه النسبة (الشكل$\PageIndex{9}$) لحساب نقطة التعادل بالدولار.

\[\text { Break-Even Point in Dollars }=\dfrac{\text { Fixed Costs }}{\text { Contribution Margin Ratio }} \label{eq1}\]

تطبيق المعادلة\ ref {eq1} على هيكس يعطي هذا الحساب:

\[\dfrac{\$ 18,000}{0.80}=\$ 22,500 \nonumber \]

سيتعين على$\$22,500$ Hicks Manufacturing تحقيق مبيعات شهرية من أجل تغطية جميع تكاليفها الثابتة. لكي نتحقق من أن نقطة التعادل لـ Hicks هي$\$22,500$ (أو$225$ الوحدات)، سننظر مرة أخرى في بيان دخل هامش المساهمة عند نقطة التعادل:

الشكل 3.2.10.jpg — الشكل$\PageIndex{10}$: بيان دخل هامش مساهمة Hicks Manufacturing عند نقطة التعادل

من خلال معرفة مستوى المبيعات الكافية لتغطية النفقات الثابتة أمر بالغ الأهمية، لكن الشركات تريد أن تكون قادرة على تحقيق الربح ويمكنها استخدام تحليل التعادل هذا لمساعدتها.

فكر مليًا: تكلفة قص الشعر

أنت مدير صالون لتصفيف الشعر وتريد معرفة عدد قصات الشعر للسيدات التي يحتاج صالونك إلى بيعها في الشهر من أجل تغطية التكاليف الثابتة لتشغيل الصالون. لقد قررت أنه بالسعر الحالي$\$35$ لكل قصة شعر، لديك$\$20$ تكاليف متغيرة مرتبطة بكل قصة. تشمل هذه التكاليف المتغيرة أجور المصمم ومنتجات الشعر ومستلزمات المتاجر. التكاليف الثابتة الخاصة بك هي$\$3,000$ شهريًا. يمكنك إجراء تحليل التعادل على أساس كل وحدة واكتشاف ما يلي:

الشكل 3.2.11.png — الشكل$\PageIndex{11}$: تحليل التعادل في صالون الشعر

لديك$4$ مصممون بالإضافة إلى أنك تعمل في الصالون ويفتح أبوابه 6 أيام في الأسبوع. بالنظر إلى نقطة التعادل وعدد المصممين المتاحين، هل سيكون الصالون متساويًا في أي وقت؟ إذا حدث ذلك، فما الذي يجب أن يحدث؟ ما الذي يمكن فعله لتحقيق نقطة التعادل؟

أمثلة على تأثيرات التكاليف المتغيرة والثابتة في تحديد نقطة التعادل

لا ترغب الشركات عادةً في تحقيق التعادل ببساطة، لأنها تعمل في مجال الأعمال التجارية لتحقيق الربح. يمكن أن يساعد تحليل التعادل أيضًا الشركات على تحديد مستوى المبيعات (بالدولار أو بالوحدات) المطلوب لتحقيق الربح المطلوب. تتمثل عملية احتساب مستوى الربح المطلوب في تحليل التعادل في إضافة مستوى الربح المطلوب إلى التكاليف الثابتة ثم حساب نقطة التعادل الجديدة. نحن نعلم أن شركة Hicks Manufacturing تتعادل في حمامات الطيور في$225$ بلو جاي، ولكن ماذا لو كان لديهم ربح مستهدف لشهر يوليو؟ يمكنهم ببساطة إضافة هذا الهدف إلى تكاليفهم الثابتة. من خلال حساب الربح المستهدف، سوف ينتجون ويبيعون (على أمل) حمامات الطيور الكافية لتغطية كل من التكاليف الثابتة والربح المستهدف.

إذا أراد هيكس تحقيق أرباح$\$16,000$ في شهر مايو، فيمكننا حساب نقطة التعادل الجديدة على النحو التالي:

\[ \text { Target Profit }=\dfrac{\text { Fixed costs }+\text { desired profit }}{\text { Contribution margin per unit }}=\dfrac{\$ 18,000+\$ 16,000}{\$ 80}=425 \text { units } \nonumber \]

لقد أثبتنا بالفعل أن التكاليف الثابتة يتم تغطيتها عند علامة$225$ الوحدات، لذلك ستغطي$200$ الوحدات الإضافية الربح المطلوب ($200$الوحدات$× \$80$ لكل وحدة هامش مساهمة$= \$16,000$).$\$18,000$ بدلاً من ذلك، يمكننا حساب ذلك بالدولار باستخدام نسبة هامش المساهمة.

\[ \text { Target Profit }=\dfrac{\text { Fixed costs }+\text { desired profit }}{\text { Contribution margin ratio }}=\dfrac{\$ 18,000+\$ 16,000}{0.80}=\$ 42,500 \nonumber \]

كما تم القيام به سابقًا، يمكننا تأكيد هذا الحساب باستخدام بيان دخل هامش المساهمة:

الشكل 3.2.12.jpg — الشكل$\PageIndex{12}$: بيان دخل هامش المساهمة

لاحظ أن الحسابات النموذجية تجاهلت ضرائب الدخل، مما يعني أننا كنا نبحث عن دخل تشغيلي مستهدف. ومع ذلك، قد ترغب الشركات في تحديد مستوى المبيعات الذي سيولد الربح المطلوب بعد خصم الضرائب. للعثور على نقطة التعادل عند الربح المطلوب بعد خصم الضرائب، نحتاج ببساطة إلى تحويل الربح المطلوب بعد خصم الضرائب إلى الربح المطلوب قبل الضريبة، والذي يشار إليه أيضًا باسم الدخل التشغيلي، ثم المتابعة كما في المثال. لنفترض أن هيكس يريد$\$24,000$ كسب ما بعد الضرائب، فما مستوى المبيعات (الوحدات والدولار) المطلوب لتحقيق هذا الهدف؟ أولاً، يجب تحويل أرباح ما بعد خصم الضرائب إلى الربح المطلوب قبل خصم الضرائب:

\[ \text { Pre-tax desired profit }=\dfrac{\text { After-tax profit }}{(1-\text { tax rate })} \nonumber \]

إذا كان معدل الضريبة على Hicks هو$40\%$، فإن ربح$\$24,000$ ما بعد الضريبة يساوي ربحًا قبل الضريبة قدره$\$40,000$:

\[ \$ 40,000=\dfrac{\$ 24,000}{(1-0.40)} \nonumber \]

يشير معدل الضريبة إلى مبلغ المصاريف الضريبية التي ستنتج عن أي أرباح$1-\text {tax rate}$ ويشير إلى المبلغ المتبقي بعد تحصيل المصاريف الضريبية. هذا المفهوم مشابه لشراء سلعة معروضة للبيع. إذا كانت تكلفة$\$80$ السلعة معروضة للبيع بسعر$40\%$ مخفض، فإن المبلغ الذي يتم دفعه مقابل السلعة هو$60\%$ سعر البيع، أو$\$ 48(\$ 80 \times 60 \%)$. هناك طريقة أخرى للعثور على ذلك تتضمن خطوتين. ابحث أولاً عن الخصم ($\$80 × 40\% = \$32$) ثم اطرح الخصم من سعر البيع ($\$80 – \$32 = \$48$).

تعمل الضرائب والأرباح بطريقة مماثلة. إذا علمنا أن الربح قبل الضريبة هو$\$100,000$ ومعدل الضريبة هو$30\%$، فإن النفقات الضريبية هي$\$100,000 × 30\% = \$30,000$. هذا يعني أن الدخل بعد خصم الضرائب هو$\$100,000 – \$30,000 = \$70,000$. ومع ذلك، في معظم حالات التعادل، وكذلك مجالات صنع القرار الأخرى، يكون الربح المطلوب بعد خصم الضرائب معروفًا، ويجب تحديد الربح قبل الضريبة بقسمة ربح ما بعد الضريبة على$1-\text {tax rate}$.

لتوضيح الجمع بين الربح وتأثيرات ما بعد الضريبة والحسابات اللاحقة، دعنا نعود إلى مثال Hicks Manufacturing. لنفترض أننا نريد حساب الحجم المستهدف بالوحدات والإيرادات التي يجب على هيكس بيعها لتوليد عائد ما بعد الضريبة$\$24,000$، بافتراض نفس التكاليف الثابتة لـ$\$18,000$.

نظرًا لأننا قررنا سابقًا أن$\$24,000$ ما بعد$\$40,000$ الضريبة يساوي قبل الضريبة إذا كان معدل الضريبة كذلك$40\%$، فإننا ببساطة نستخدم صيغة التعادل عند الربح المطلوب لتحديد المبيعات المستهدفة.

\[\text { Target sales }=\dfrac{\text { (Fixed costs }+\text { Desired profit) }}{\text { Contribution margin per unit }}=\dfrac{(\$ 18,000+\$ 40,000)}{\$ 80}=725 \text { units } \nonumber \]

يوضح هذا الحساب أن هيكس سيحتاج إلى بيع$725$ وحدات في$\$100$ وحدة لتوليد$\$72,500$ المبيعات لكسب$\$24,000$ أرباح ما بعد خصم الضرائب.

وبدلاً من ذلك، كان من الممكن حساب المبيعات المستهدفة بدولارات المبيعات باستخدام نسبة هامش المساهمة:

\[\text { Target sales }=\dfrac{\text { (Fixed costs + Desired profit) }}{\text { Contribution margin per unit }}=\dfrac{(\$ 18,000+\$ 40,000)}{0.80}=\$ 72,500 \nonumber \]

مرة أخرى، يثبت بيان دخل هامش المساهمة علاقات المبيعات والأرباح.

الشكل 3.2.13.jpg — الشكل$\PageIndex{13}$: بيان دخل هامش المساهمة

وبالتالي، لحساب نقطة التعادل في دخل معين بعد خصم الضرائب، فإن الخطوة الإضافية الوحيدة هي تحويل الدخل بعد خصم الضرائب إلى دخل قبل خصم الضرائب قبل استخدام صيغة التعادل. من الجيد فهم تأثير الضرائب على تحليل التعادل لأن الشركات غالبًا ما ترغب في التخطيط بناءً على تأثيرات ما بعد الضريبة للقرار حيث أن جزء الدخل بعد خصم الضرائب هو الجزء الوحيد من الدخل الذي سيكون متاحًا للاستخدام في المستقبل.

تطبيق مفاهيم التعادل لمنظمة الخدمة

نظرًا لأن تحليل التعادل ينطبق على أي مؤسسة تجارية، يمكننا تطبيق هذه المبادئ نفسها على منظمة خدمية. على سبيل المثال، Marshall & Hirito هي شركة محاسبة متوسطة الحجم تقدم مجموعة واسعة من الخدمات المحاسبية لعملائها ولكنها تعتمد بشكل كبير على إعداد ضريبة الدخل الشخصية في معظم إيراداتها. لقد قاموا بتحليل التكلفة التي تتحملها الشركة المرتبطة بإعداد هذه العوائد. لقد حددوا هيكل التكلفة التالي لإعداد إقرار ضريبة الدخل الفردي القياسي 1040A:

الشكل 3.2.14.jpg — الشكل$\PageIndex{14}$: هيكل التكلفة لإعداد معيار 1040A لإقرار ضريبة الدخل الفردي

لديهم تكاليف ثابتة$\$14,000$ شهريًا مرتبطة برواتب المحاسبين المسؤولين عن إعداد النموذج 1040A. من أجل تحديد نقطة التعادل الخاصة بهم، يقومون أولاً بتحديد هامش المساهمة للنموذج 1040A كما هو موضح:

الشكل 3.2.15.jpg — الشكل$\PageIndex{15}$: هامش المساهمة للنموذج 1040A

الآن يمكنهم حساب نقطة التعادل الخاصة بهم:

\[\text { Break-Even Point in Units }=\dfrac{\text { Total fixed costs }}{\text { Contribution margin per unit }}=\dfrac{\$ 14,000}{\$ 250}=56 \text { returns } \nonumber \]

تذكر أن هذه هي نقطة التعادل في الوحدات (عدد الإقرارات الضريبية) ولكن يمكنهم أيضًا العثور على نقطة التعادل المعبر عنها بالدولار باستخدام نسبة هامش المساهمة. أولاً، يجدون نسبة هامش المساهمة. ثم يستخدمون النسبة لحساب نقطة التعادل بالدولار:

\[\text { Break-Even Point in Dollars }=\dfrac{\text { Fixed costs }}{\text { Contribution margin ratio }}=\dfrac{\$ 14,000}{0.625}=\$ 22,400 \nonumber \]

يمكننا تأكيد هذه الأرقام من خلال إعداد بيان دخل هامش المساهمة:

الشكل 3.2.16.jpg — الشكل$\PageIndex{16}$: بيان دخل هامش المساهمة

لذلك، طالما قامت شركة Marshall & Hirito بإعداد$56$ نموذج 1040 لإقرارات ضريبة الدخل، فلن يكسبوا أي ربح ولكنهم أيضًا لن يتكبدوا أي خسارة. ماذا لو كان لدى مارشال آند هيريتو ربح شهري مستهدف قدره$\$10,000$؟ يمكنهم استخدام عملية تحليل التعادل لتحديد عدد العوائد التي سيحتاجون إلى إعدادها لتغطية نفقاتهم الثابتة والوصول إلى الربح المستهدف:

\[\text { Target Profit }=\dfrac{\text { Fixed costs }+\text { desired profit }}{\text { Contribution margin per unit }}=\dfrac{\$ 14,000+\$ 10,000}{\$ 250}=96 \text { returns } \nonumber \]

سوف يحتاجون إلى إعداد$96$ العوائد خلال الشهر من أجل تحقيق$\$10,000$ الربح. يتطلب التعبير عن ذلك بالدولار بدلاً من الوحدات أن نستخدم نسبة هامش المساهمة كما هو موضح:

\[\text { Target Profit }=\dfrac{\text { Fixed costs }+\text { desired profit }}{\text { Contribution margin per unit }}=\dfrac{\$ 14,000+\$ 10,000}{0.625}=\$ 38,400 \nonumber \]

تعرف شركة Marshall & Hirito الآن أنه من أجل تغطية التكاليف الثابتة المرتبطة بهذه الخدمة، يجب أن تحقق$\$38,400$ أرباحًا. مرة أخرى، دعنا نتحقق من ذلك من خلال إنشاء بيان دخل هامش المساهمة:

الشكل 3.2.17.jpg — الشكل$\PageIndex{17}$: بيان دخل هامش المساهمة

كما ترى، فإن الإيرادات$\$38,400$ الزائدة لن تغطي التكاليف الثابتة فحسب، بل ستزود مارشال وهيريتو بالربح (صافي الدخل) الذي$\$10,000$ يرغبون فيه.$\$14,000$

كما تعلمت، يمكن حساب التعادل باستخدام هامش المساهمة لكل وحدة أو نسبة هامش المساهمة. الآن بعد أن رأيت هذه العملية، دعونا نلقي نظرة على مثال لهذين المفهومين المقدمين معًا لتوضيح كيف ستوفر أي من الطريقتين نفس النتائج المالية.

لنفترض أن Channing's Chairs تصمم وتبني وتبيع كراسي مكتب مريحة فريدة للمنزل والعمل. كرسيهم الأكثر مبيعًا هو Spine Saver. $\PageIndex{18}$يوضح الشكل كيف يمكن لـ Channing تحديد نقطة التعادل في دولارات المبيعات باستخدام هامش المساهمة لكل وحدة أو نسبة هامش المساهمة.

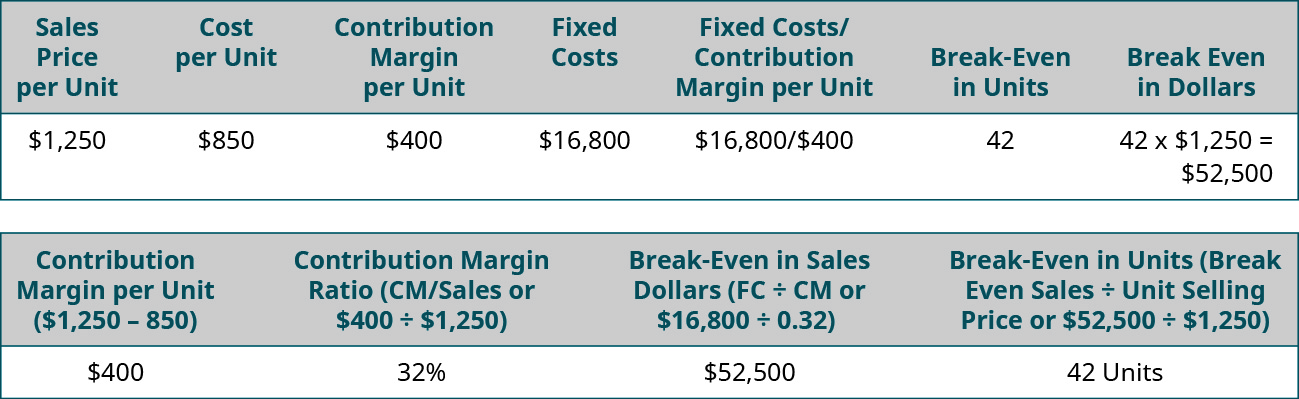
سعر البيع لكل وحدة 1,250 دولارًا، التكلفة لكل وحدة 850 دولارًا، هامش المساهمة لكل وحدة 400 دولار، التكاليف الثابتة 16,800 دولار، التكلفة الثابتة مقسومًا على هامش المساهمة لكل وحدة 16,800 دولار مقسومًا على 400 دولار، التعادل في الوحدات 42، التعادل بالدولار 42 مرة، 1,250 دولارًا يساوي 52,500 دولار، نسبة هامش المساهمة (CM مقسومًا على المبيعات أو 400 دولار) مقسومًا على 1,250 دولارًا) 32 بالمائة، التعادل في دولارات المبيعات (FC مقسومًا على CM) أو 16,800 دولار مقسومًا على 0.32 يساوي 52,500 دولار، التعادل في الوحدات (مبيعات التعادل مقسومًا على سعر بيع الوحدة أو 42,500 دولار مقسومًا على 1,250 دولارًا تساوي 42 وحدة. — الشكل$\PageIndex{18}$: نقطة التعادل في تشانينج. (الإسناد: حقوق الطبع والنشر لجامعة رايس، أوبن ستاإكس، بموجب ترخيص CC BY-NC-SA 4.0)

لاحظ أنه في أي من السيناريوهين، تكون نقطة التعادل هي نفسها بالدولار والوحدات، بغض النظر عن النهج. وبالتالي، يمكنك دائمًا العثور على نقطة التعادل (أو الربح المطلوب) بالوحدات ثم تحويلها إلى مبيعات عن طريق الضرب في سعر البيع لكل وحدة. بدلاً من ذلك، يمكنك العثور على نقطة التعادل في دولارات المبيعات ثم العثور على عدد الوحدات بالقسمة على سعر البيع لكل وحدة.

مثال$\PageIndex{1}$: College Creations

تقوم College Creations, Inc (CC) ببناء دور علوي يمكن تكييفه بسهولة مع معظم غرف النوم أو الشقق ويمكن تجميعه في مجموعة متنوعة من التكوينات. يتم بيع كل دور علوي$\$500$، وتكلفة إنتاج دور علوي واحد هي$\$300$، بما في ذلك جميع الأجزاء والعمالة. لدى CC تكاليف ثابتة تبلغ$\$100,000$.

ماذا يحدث إذا لم ينتج CC شيئًا؟
الآن، افترض أن CC تنتج وتبيع وحدة واحدة (دور علوي). ما هي نتائجها المالية؟
الآن، ماذا تعتقد أنه سيحدث إذا قاموا بإنتاج وبيع 501 وحدة؟
كم عدد الوحدات التي ستحتاج CC إلى بيعها من أجل تحقيق التعادل؟
كم عدد الوحدات التي ستحتاج CC إلى بيعها إذا أرادت الحصول على ربح قبل الضريبة$\$50,000$؟

الحل

إذا لم ينتجوا شيئًا، فسيظلون يتحملون تكاليف ثابتة قدرها$\$100,000$. سوف يعانون من خسارة صافية قدرها$\$100,000$.
إذا قاموا ببيع وحدة واحدة، فسيكون لديهم خسارة صافية قدرها$\$99,800$.

الشكل 3.2.19.png — الشكل$\PageIndex{19}$: النتائج المالية لـ CC

إذا قاموا بإنتاج$501$ وحدات، فسيكون لديهم دخل تشغيلي$\$200$ كما هو موضح:

الشكل 3.2.20.png — الشكل$\PageIndex{20}$: النتائج المالية لـ CC

يمكن تحديد التعادل بواسطة FC/CM لكل وحدة: $\$ 100,000 \div \$ 200=500$. يجب بيع خمسمائة طابق علوي لتحقيق التعادل.
يمكن التعامل مع الربح المطلوب كتكلفة ثابتة، وسيكون الربح المستهدف (FC + الربح المطلوب) /CM أو ($\$100,000 + \$50,000) ÷ \$200 = 750$. يجب بيع سبعمائة وخمسين طابقًا للوصول إلى الدخل المطلوب$\$50,000$. هناك طريقة أخرى لمعرفة ذلك وهي معرفة أنه بعد استيفاء التكاليف الثابتة، سيتجه هامش المساهمة$\$200$ لكل وحدة نحو الربح. الربح المطلوب من$\$50,000 ÷ \$200 \text { per unit contribution margin } = 250$. هذا يعني أنه يجب بيع وحدات$250$ إضافية. يتطلب تحقيق التعادل بيع$500$ الوحدات، والوصول إلى الربح المطلوب$\$50,000$ يتطلب$250$ وحدات إضافية، ليصبح المجموع الكلي$750$ للوحدات.

المساهمون والصفات

Template:contribmanagerialaccountingopenstax