Skip to main content
Global

7.6: حل تطبيقات باستخدام المعادلات الكسرية

  1. Last updated
  2. Save as PDF
  • Page ID
    201704

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم
    • حل النسب
    • حل تطبيقات الأشكال المتشابهة
    • حل تطبيقات الحركة الموحدة
    • حل تطبيقات العمل
    • حل مشاكل الاختلاف المباشر
    • حل مسائل التباين العكسي
    ملاحظة

    قبل البدء، قم بإجراء اختبار الاستعداد هذا.

    1. المثال 2.2.13. المثال 2.5.13. المثال 2.2.9.

    حل النسب

    عندما يكون التعبيران العقليان متساويين، فإن المعادلة المتعلقة بهما تسمى النسبة.

    نسبة

    النسبة هي معادلة الشكل\(\dfrac{a}{b}=\dfrac{c}{d}\)، أين\(b \neq 0, d \neq 0\).

    تتم قراءة النسبة «\(a\)\(b\)كما\(c\) هي»\(d\).

    المعادلة\(\dfrac{1}{2}=\dfrac{4}{8}\) عبارة عن نسبة لأن الكسرين متساويان. \(\dfrac{1}{2}=\dfrac{4}{8}\)تتم قراءة النسبة «1 إلى 2 حيث أن 4 هي إلى 8.»

    نظرًا لأن النسبة هي معادلة ذات تعبيرات كسرية، فسوف نحل النسب بنفس الطريقة التي حللنا بها المعادلات الكسرية. سنضرب طرفي المعادلة في شاشة LCD لمسح الكسور ثم حل المعادلة الناتجة.

    مثال\(\PageIndex{1}\)

    حل:\(\dfrac{n}{n+14}=\dfrac{5}{7}\).

    الحل

    \[\dfrac{n}{n+14}=\dfrac{5}{7}, \quad n \neq-14 \nonumber \]

    اضرب كلا الجانبين بواسطة شاشة LCD.

    \[7(n+14)\left(\dfrac{n}{n+14}\right)=7(n+14)\left(\dfrac{5}{7}\right) \nonumber \]

    قم بإزالة العوامل المشتركة على كل جانب.

    \[7 n=5(n+14) \nonumber \]

    قم بالتبسيط.

    \[7 n=5 n+70 \nonumber \]

    حل لـ\(n\).

    \[\begin{aligned} 2n&=70\\ n&=35 \end{aligned} \nonumber \]

    تحقق.

    \[\dfrac{n}{n+14}=\dfrac{5}{7} \nonumber \]

    بديل\(n=35\)

    \[\dfrac{35}{35+14} \overset{?}{=} \dfrac{5}{7} \nonumber \]

    قم بالتبسيط.

    \[\dfrac{35}{49} \overset{?}{=} \dfrac{5}{7} \nonumber \]

    أظهر العوامل المشتركة.

    \[\dfrac{5 \cdot 7}{7 \cdot 7} \overset{?}{=} \dfrac{5}{7} \nonumber \]

    قم بالتبسيط.

    \[\dfrac{5}{7}=\dfrac{5}{7}\; \surd \nonumber \]

    التمارين\(\PageIndex{1}\)

    حل النسبة:\(\dfrac{y}{y+55}=\dfrac{3}{8}\).

    إجابة

    \(y=33\)

    التمارين\(\PageIndex{2}\)

    حل النسبة:\(\dfrac{z}{z-84}=-\dfrac{1}{5}\).

    إجابة

    \(z=14\)

    لاحظ في المثال الأخير أنه عندما قمنا بمسح الكسور بالضرب في شاشة LCD، فإن النتيجة هي نفسها كما لو كنا قد ضربنا بشكل متقاطع.

    \[\begin{aligned} \dfrac{n}{n+14}=\dfrac{5}{7} \quad \quad \quad \dfrac{n}{n+14}=\dfrac{5}{7} \\ 7(n+14)\left(\dfrac{n}{n+14}\right)=7(n+14)\left(\dfrac{5}{7}\right) \quad \quad \quad \dfrac{n}{n+14}=\dfrac{5}{7} \\ 7n=5(n+14) \quad \quad \quad 7n=5(n+14) \end{aligned} \nonumber \]

    بالنسبة لأي نسبة\(\dfrac{a}{b}=\dfrac{c}{d}\)، نحصل على نفس النتيجة عندما نزيل الكسور بالضرب في شاشة LCD كما هو الحال عند الضرب المتقاطع.

    \[\begin{aligned} \dfrac{a}{b} =\dfrac{c}{d} \quad \quad \quad \dfrac{a}{b}=\dfrac{c}{d} \\ bd\left(\dfrac{a}{b}=\frac{c}{d}\right) bd \quad \quad \quad \frac{a}{b} = \frac{c}{d} \\ ad =bc \quad \quad \quad ad=bc \end{aligned} \nonumber \]

    لحل التطبيقات ذات النسب، سنتبع استراتيجيتنا المعتادة لحل التطبيقات ولكن عندما نقوم بإعداد النسبة، يجب أن نتأكد من صحة الوحدات - يجب أن تتطابق الوحدات في البسط مع بعضها البعض ويجب أن تتطابق الوحدات في القواسم أيضًا مع بعضها البعض.

    عندما يصف أطباء الأطفال الأسيتامينوفين للأطفال، فإنهم يصفون 5 مليلتر (مل) من الأسيتامينوفين لكل 25 رطلاً من وزن الطفل. إذا كان وزن زوي 80 رطلاً، فما عدد الملليلترات من الأسيتامينوفين التي سيصفها طبيبها؟

    الحل

    حدد ما يُطلب منا العثور عليه، واختر متغيرًا لتمثيله.

    كم مل من الأسيتامينوفين سيصفه الطبيب؟

    كمية\(a=ml\) كبيرة من الأسيتامينوفين.

    اكتب جملة تعطي المعلومات للعثور عليها.

    إذا تم وصف 5 مل لكل 25 رطلاً، فما المقدار الذي سيُوصف مقابل 80 رطلاً؟

    ترجم إلى نسبة - احذر من الوحدات.

    الخطوة 1. اكتب عدم المساواة في صورة حاصل قسمة واحد على اليسار وصفر على اليمين. عدم المساواة لدينا في هذا الشكل.

    \[\dfrac{x-1}{x+3} \geq 0 \nonumber \]

    الخطوة 2. حدد النقاط الحرجة - النقاط التي سيكون فيها التعبير العقلاني صفرًا أو غير محدد.

    سيكون التعبير العقلاني صفرًا عندما يكون البسط صفرًا. منذ\(x-1=0\) متى\(x=1\)، أصبحت 1 نقطة حرجة. لن يتم تعريف التعبير العقلاني عندما يكون المقام صفرًا. منذ\(x+3=0\) متى\(x=-3\)، تعد -3 نقطة حرجة.

    الخطوة 3. استخدم النقاط الحرجة لتقسيم خط الأرقام إلى فواصل زمنية.

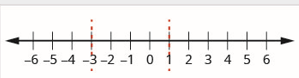
    clipboard_ee2fe708799269f0539168f8443a351d2.png

    الخطوة 4. تظهر فوق خط الأعداد علامة كل عامل من عوامل التعبير العقلاني في كل فاصل زمني. أسفل خط الأرقام تظهر علامة حاصل القسمة.

    استخدم القيم في كل فاصل زمني لتحديد قيمة كل عامل في الفاصل الزمني. في الفاصل الزمني (-3,1)، يعد الصفر قيمة جيدة للاختبار. على سبيل المثال، عندما يكون\(x+3=3\) العامل\(x=0\) حينها\(x-1=-1\)\(x-1\) ويكون العامل سلبيًا\(x+3\) وإيجابيًا. نظرًا لأن السالب مقسومًا على موجب يكون سالبًا، يتم وضع علامة سالب على حاصل القسمة في تلك الفترة.

    الخطوة 5. حدد الفترات التي يكون فيها عدم المساواة صحيحًا. اكتب الحل بالتدوين الفاصل الزمني.

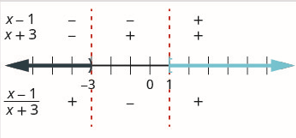
    clipboard_edae13eef9fc14a8139b8d2bcd44dd965.png

    نريد أن يكون حاصل القسمة أكبر من أو يساوي الصفر، وبالتالي فإن الأرقام في الفواصل الزمنية\((-\infty,-3)\)\((1, \infty)\) هي حلول. نظرًا لأنه يجب استبعاد 3 نظرًا لأنه يجعل التعبير العقلاني 0، فلا يمكننا تضمينه في الحل. يمكننا تضمين 1 في الحل الخاص بنا.

    \[(-\infty,-3) \cup[1, \infty) \nonumber \]

    اضرب كلا الجانبين في شاشة LCD، 400. قم بإزالة العوامل المشتركة على كل جانب. قم بالتبسيط ولكن لا تتضاعف على اليسار. لاحظ ما ستكون الخطوة التالية.

    \[16 \cdot 5=5 a \nonumber \]

    حل لـ\(a\).

    \[\begin{aligned} \dfrac{16 \cdot 5}{5}&=\dfrac{5 a}{5}\\ 16&=a \end{aligned} \nonumber \]

    تحقق. هل الإجابة معقولة؟ اكتب جملة كاملة.

    سيصف طبيب الأطفال 16 مل من الأسيتامينوفين إلى زوي.

    التمارين\(\PageIndex{3}\)

    يصف أطباء الأطفال 5 مليلتر (مل) من الأسيتامينوفين لكل 25 رطلاً من وزن الطفل. كم مليلتر من الأسيتامينوفين الذي سيصفه الطبيب لإميليا، التي تزن 60 رطلاً؟

    إجابة

    سيصف طبيب الأطفال 12 مل من الأسيتامينوفين لإميليا.

    التمارين\(\PageIndex{4}\)

    لكل كيلوغرام واحد (كجم) من وزن الطفل، يصف أطباء الأطفال 15 ملليغرام (ملغ) من مخفض الحمى. إذا كانت إيزابيلا تزن 12 كجم، فما عدد الملليغرامات من مخفض الحمى الذي سيصفه طبيب الأطفال؟

    إجابة

    سيصف طبيب الأطفال 180 ملغ من مخفض الحمى لإيزابيلا.

    حل تطبيقات الأشكال المتشابهة

    عندما تقوم بتقليص صورة أو تكبيرها على هاتف أو جهاز لوحي، أو تحديد مسافة على الخريطة، أو استخدام نمط لإنشاء خزانة كتب أو خياطة فستان، فأنت تعمل بأشكال مماثلة. إذا كان هناك شخصان لهما نفس الشكل تمامًا، ولكن بأحجام مختلفة، يُقال إنهما متشابهان. أحدهما نموذج مصغر للآخر. جميع الزوايا المقابلة لها نفس المقاييس والجوانب المقابلة لها نفس النسبة.

    شخصيات مماثلة

    يتشابه الشكلان إذا كانت قياسات الزوايا المقابلة متساوية وكانت الجوانب المقابلة لهما نفس النسبة.

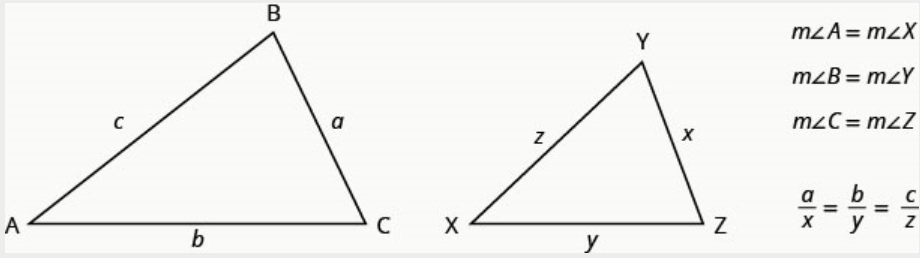
    على سبيل المثال، المثلثان في الشكل أدناه متشابهان. يبلغ \(\Delta ABC\)طول كل جانب أربعة أضعاف طول الجانب المقابل لـ \(\Delta XYZ\).

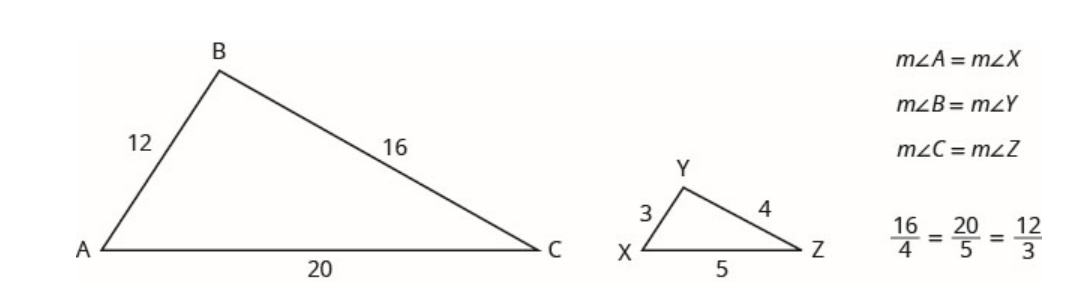
    clipboard_e856a7de8b3a79dcd08723d9871ccd270.png

    يتم تلخيص ذلك في خاصية المثلثات المتشابهة.

    خاصية المثلثات المتشابهة

    إذا كانت\(\Delta ABC\) مشابهة لـ\(\Delta XYZ\)، فإن قياس الزاوية المقابل لها يكون متساويًا وتكون الجوانب المقابلة لها نفس النسبة.

    clipboard_e4fdc3b30588979c50d44a48aef0d74a0.png

    لحل التطبيقات ذات الأرقام المتشابهة، سنتبع استراتيجية حل المشكلات لتطبيقات الهندسة التي استخدمناها سابقًا.

    مثال\(\PageIndex{3}\)

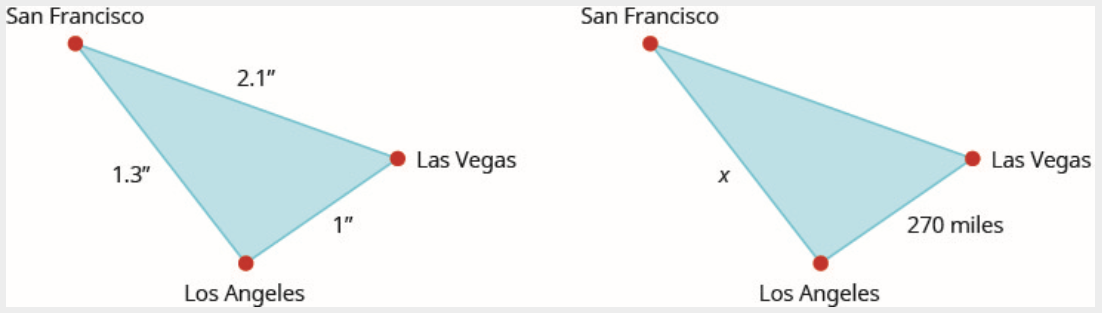
    على الخريطة، تشكل سان فرانسيسكو ولاس فيغاس ولوس أنجلوس مثلثًا. يتم قياس المسافة بين المدن بالبوصة. يمثل الشكل الموجود على اليسار أدناه المثلث الذي شكلته المدن على الخريطة. إذا كانت المسافة الفعلية من لوس أنجلوس إلى لاس فيغاس 270 ميلًا، فأوجد المسافة من لوس أنجلوس إلى سان فرانسيسكو.

    clipboard_efb0263e1d94381d6b9257775d879ded0.png

    الحل

    نظرًا لأن المثلثات متشابهة، فإن الجوانب المقابلة متناسبة.

    اقرأ المشكلة. ارسم الأشكال وقم بتسميتها بالمعلومات المعطاة. الأرقام موضحة أعلاه.

    حدد ما نبحث عنه: المسافة الفعلية من لوس أنجلوس إلى سان فرانسيسكو

    قم بتسمية المتغيرات: Let\(x\) = المسافة من لوس أنجلوس إلى سان فرانسيسكو.

    ترجم إلى معادلة. نظرًا لأن المثلثات متشابهة، فإن الجوانب المقابلة متناسبة. سنجعل البسطين «أميالًا» والمقامات «بوصات».

    \[$\dfrac{x \text { miles }}{1.3 \text { inches }}=\dfrac{270 \text { miles }}{1 \text { inch }}$ \nonumber \]

    حل المعادلة.

    \[\begin{aligned} 1.3\left(\dfrac{x}{1.3}\right)&=1.3\left(\dfrac{270}{1}\right) \\ x&=351 \end{aligned} \nonumber \]

    تحقق. على الخريطة، المسافة من لوس أنجلوس إلى سان فرانسيسكو هي أكثر من المسافة من لوس أنجلوس إلى لاس فيغاس. نظرًا لأن 351 هو أكثر من 270، فإن الإجابة منطقية.

    تحقق\(x=351\) من النسبة الأصلية. استخدم الآلة الحاسبة.

    \[\begin {aligned} \dfrac{x \text { miles }}{1.3 \text { inches }}&=\dfrac{270 \text { miles }}{1 \text { inch }}\\ \dfrac{351 \text { miles }}{1.3 \text { inches }} &\overset{?}{=} \dfrac{270 \text { miles }}{1 \text { inch }}\\ \dfrac{270 \text { miles }}{1 \text { inch }}&=\dfrac{270 \text { miles }}{1 \text { inch }} \surd \end{aligned} \nonumber \]

    أجب عن السؤال: المسافة من لوس أنجلوس إلى سان فرانسيسكو هي 351 ميلاً.

    على الخريطة، تشكل سياتل وبورتلاند وبويز مثلثًا. يتم قياس المسافة بين المدن بالبوصة. يمثل الشكل الموجود على اليسار أدناه المثلث الذي شكلته المدن على الخريطة. المسافة الفعلية من سياتل إلى بويز هي 400 ميل.

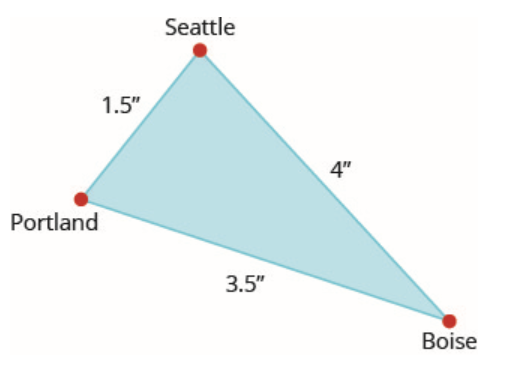
    clipboard_e545a49106f741f6a3b36f53e39ed4458.png

    التمارين\(\PageIndex{5}\)

    ابحث عن المسافة الفعلية من سياتل إلى بورتلاند.

    إجابة

    المسافة هي 150 ميلا.

    التمارين\(\PageIndex{6}\)

    ابحث عن المسافة الفعلية من بورتلاند إلى بويز.

    إجابة

    المسافة هي 350 ميلا.

    يمكننا استخدام أرقام مماثلة للعثور على ارتفاعات لا يمكننا قياسها مباشرة.

    مثال\(\PageIndex{4}\)

    يبلغ طول تايلر 6 أقدام. في وقت متأخر من بعد ظهر أحد الأيام، كان طوله 8 أقدام. في نفس الوقت، كان ظل الشجرة يبلغ طوله 24 قدمًا. أوجد ارتفاع الشجرة.

    الحل

    اقرأ المشكلة وارسم الشكل. نحن نبحث\(h\) عن ارتفاع الشجرة.

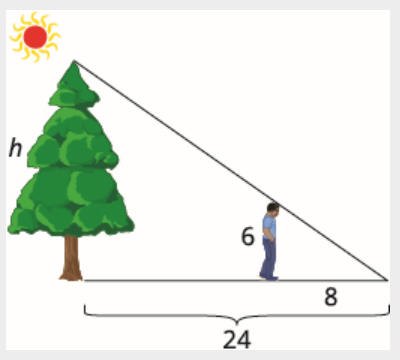
    clipboard_ee900ec650dd61d33cbc8b7d340874f27.png

    سنستخدم مثلثات متشابهة لكتابة معادلة. المثلث الصغير يشبه المثلث الكبير.

    \[\dfrac{h}{24}=\dfrac{6}{8} \nonumber \]

    حل النسبة.

    \[\begin {aligned} 24\left(\dfrac{6}{8}\right)&=24\left(\dfrac{h}{24}\right)\\ 18&=h \end{aligned} \nonumber \]

    قم بالتبسيط. تحقق.

    ارتفاع تايلر أقل من طول ظله لذلك فمن المنطقي أن يكون ارتفاع الشجرة أقل من طول ظلها. تحقق\(h=18\) من النسبة الأصلية.

    \[\begin{aligned} &\dfrac{6}{8}=\dfrac{h}{24}\\ &\dfrac{6}{8} \overset{?}{=} \dfrac{18}{24}\\ &\dfrac{3}{4}=\dfrac{3}{4} \surd \end{aligned} \nonumber \]

    التمارين\(\PageIndex{7}\)

    يلقي عمود الهاتف ظلًا يبلغ طوله 50 قدمًا. وفي الجوار، تلقي إشارة مرور طولها 8 أقدام بظلالها على طول 10 أقدام. كم يبلغ طول عمود الهاتف؟

    إجابة

    يبلغ طول عمود الهاتف 40 قدمًا.

    التمارين\(\PageIndex{8}\)

    تلقي شجرة صنوبر بظلالها على 80 قدمًا بجوار مبنى يبلغ ارتفاعه 30 قدمًا يلقي بظلاله على 40 قدمًا. كم يبلغ ارتفاع شجرة الصنوبر؟

    إجابة

    يبلغ طول شجرة الصنوبر 60 قدمًا.

    حل تطبيقات الحركة الموحدة

    لقد قمنا بحل مشاكل الحركة المنتظمة باستخدام الصيغة\(D=r t\) في الفصول السابقة. استخدمنا جدولًا مثل الجدول أدناه لتنظيم المعلومات وقيادتنا إلى المعادلة.

    معدل\(\cdot\) الوقت = المسافة
      \ (\ cdot\) الوقت = المسافة» class= lt-math-14671>    
      \ (\ cdot\) الوقت = المسافة» class= lt-math-14671>    

    \(D=r t\)تفترض الصيغة أننا نعرفها\(r\)\(t\) ونستخدمها للبحث عنها\(D\). إذا كنا نعرف\(D\)\(r\) ونحتاج إلى البحث\(t\)، فسنحل المعادلة\(t\) ونحصل على الصيغة\(t=\dfrac{D}{r}\).

    لقد شرحنا أيضًا كيف يؤثر الطيران مع الرياح أو ضدها على سرعة الطائرة. سنعيد النظر في هذه الفكرة في المثال التالي.

    مثال\(\PageIndex{5}\)

    يمكن للطائرة أن تطير لمسافة 200 ميل في اتجاه الريح المعاكس بسرعة 30 ميلاً في الساعة في نفس الوقت الذي تستغرقه في الطيران لمسافة 300 ميل مع رياح خلفية تبلغ 30 ميلاً في الساعة. ما سرعة الطائرة؟

    الحل

    هذه حالة حركة موحدة. سيساعدنا الرسم التخطيطي على تصور الموقف.

    clipboard_e675478d490b6955418a9d40f7346c6b5.png

    نقوم بملء المخطط لتنظيم المعلومات.

    نحن نبحث عن سرعة الطائرة. دعونا\(r\) = سرعة الطائرة.

    عندما تطير الطائرة مع الريح، تزيد الرياح من سرعتها وبالتالي يكون المعدل\(r + 30\).

    عندما تطير الطائرة ضد الريح، تقلل الرياح من سرعتها ويكون المعدل كذلك\(r − 30\).

    اكتب في الأسعار. اكتب في المسافات. منذ ذلك الحين\(D=r \cdot t\)، نحل المشكلة\(t\) ونحصل عليها\(t=\dfrac{D}{r}\). نقسم المسافة على المعدل في كل صف، ونضع التعبير في عمود الوقت.

    معدل\(\cdot\) الوقت = المسافة
    الرياح المعاكسة \ (\ cdot\) الوقت = المسافة>\(r-30\) \(\dfrac{200}{r-30}\) 200
    الرياح الخلفية \ (\ cdot\) الوقت = المسافة>\(r+30\) \(\dfrac{300}{r+30}\) 300

    نحن نعلم أن الأوقات متساوية ولذلك نكتب المعادلة.

    \[\dfrac{200}{r-30}=\dfrac{300}{r+30} \nonumber \]

    نضرب كلا الجانبين بواسطة شاشة LCD.

    \[(r+30)(r-30)\left(\frac{200}{r-30}\right)=(r+30)(r-30)\left(\frac{300}{r+30}\right) \nonumber \]

    قم بالتبسيط والحل.

    \[\begin{aligned} (r+30)(200)&=(r-30) 300 \\ 200 r+6000&=300 r-9000 \\ 15000&=100 r \end{aligned} \nonumber \]

    تحقق.

    هل\(150 \mathrm{mph}\) السرعة معقولة للطائرة؟ نعم. إذا كانت الطائرة تسير\(150 \mathrm{mph}\) والرياح هي\(30 \mathrm{mph}\)،

    \[\text { Tailwind } \quad 150+30=180 \mathrm{mph} \quad \dfrac{300}{180}=\dfrac{5}{3} \text { hours } \nonumber \]

    \[\text { Headwind } 150-30=120 \mathrm{mph} \dfrac{200}{120}=\dfrac{5}{3} \text { hours } \nonumber \]

    الأوقات متساوية، لذا فهي تتحقق. كانت الطائرة مسافرة\(150 \mathrm{mph}\).

    التمارين\(\PageIndex{9}\)

    يمكن لـ Link ركوب دراجته 20 ميلًا في رياح عكسية بسرعة 3 ميل في الساعة في نفس الفترة الزمنية التي يمكنه ركوبها 30 ميلًا مع رياح خلفية 3 ميل في الساعة. ما هي سرعة ركوب الدراجات في Link؟

    إجابة

    تبلغ سرعة ركوب الدراجات في Link 15 ميلاً في الساعة.

    التمارين\(\PageIndex{10}\)

    تستطيع دانيكا أن تبحر بقاربها 5 أميال في رياح عكسية تبلغ سرعتها 7 ميل في الساعة في نفس الوقت الذي تستطيع فيه الإبحار 12 ميلاً مع رياح خلفية تبلغ سرعتها 7 ميل في الساعة. ما هي سرعة قارب دانيكا بدون ريح؟

    إجابة

    تبلغ سرعة قارب دانيكا 17 ميلاً في الساعة.

    في المثال التالي، سنعرف الوقت الإجمالي الناتج عن السفر لمسافات مختلفة بسرعات مختلفة.

    مثال\(\PageIndex{6}\)

    تدرب جاسمين لمدة 3 ساعات يوم السبت. ركضت 8 أميال ثم ركبت الدراجة 24 ميلاً. سرعة ركوب الدراجات لديها أسرع بـ 4 ميل في الساعة من سرعة ركضها. ما هي سرعة ركضها؟

    الحل

    هذه حالة حركة موحدة. سيساعدنا الرسم التخطيطي على تصور الموقف.

    clipboard_ea415f63ad2acc69c7ea17326f1ee0337.png

    نقوم بملء المخطط لتنظيم المعلومات. نحن نبحث عن سرعة تشغيل Jazmine. Let\(r\) = سرعة تشغيل Jazmine.

    سرعة ركوب الدراجات لديها أسرع بـ 4 أميال من سرعة ركضها. \(r + 4\)= سرعة ركوب الدراجات

    يتم إعطاء المسافات، أدخلها في المخطط. منذ ذلك الحين\(D=r \cdot t\)، نحل المشكلة\(t\) ونحصل عليها\(t=\dfrac{D}{r}\). نقسم المسافة على المعدل في كل صف، ونضع التعبير في عمود الوقت.

    معدل\(\cdot\) الوقت = المسافة
    اركض \ (\ cdot\) الوقت = المسافة>\(r\) \(\dfrac{8}{r}\) 8
    دراجة \ (\ cdot\) الوقت = المسافة>\(r+4\) \(\dfrac{24}{r+4}\) 24
      \ (\ cdot\) الوقت = المسافة> 3  

    اكتب جملة كلمة: وقتها بالإضافة إلى وقت ركوب الدراجات هو 3 ساعات.

    ترجم الجملة للحصول على المعادلة.

    \[\dfrac{8}{r}+\dfrac{24}{r+4}=3 \nonumber \]

    حل.

    \ [\ ابدأ {محاذاة}
    r (r+4)\ يسار (\ dfrac {8} {r} +\ dfrac {24} {r+4}\ يمين) &=3\ cdot r (r+4)\\
    8 (r+4) +3 r (r+4)\\
    8 r+32+24 ص &=3 r^ {2}
    ++32 ص =3 r^ {2} +12 r\\\
    0 &=3 r^ {2} -20 r-32\\\
    0 & =( 3 r+ 4) (r-8)
    \ النهاية {محاذاة}\ بدون رقم\]

    \[\begin{array}{lc} {(3 r+4)=0} & {(r-8)=0} \\ \cancel{r=\dfrac{4}{3}} \quad & {r=8} \end{array} \nonumber \]

    تحقق.

    السرعة السلبية لا معنى لها في هذه المشكلة،\(r=8\) وكذلك الحل.

    هل 8 ميل في الساعة هي سرعة تشغيل معقولة؟ نعم.

    إذا كان معدل تشغيل Jazmine هو 4، ثم معدل ركوب الدراجات لها\(r+4\)، وهو\(8+4=12\).

    \[\text { Run } 8 \mathrm{mph} \quad \dfrac{8 \mathrm{miles}}{8 \mathrm{mph}}=1 \text { hour } \nonumber \]

    \[\text { Bike } 12 \text { mph } \quad \dfrac{24 \text { miles }}{12 \mathrm{mph}}=2 \text { hours } \nonumber \]

    \(y=\dfrac{k}{x}\)