7.2: ضرب التعبيرات الكسرية وقسمتها
- Page ID
- 201742
في نهاية هذا القسم، ستكون قادرًا على:
- حدد القيم التي لا يتم تعريف التعبير العقلاني لها
- تبسيط التعبيرات العقلانية
- اضرب التعبيرات العقلانية
- اقسم التعبيرات العقلانية
- ضرب الوظائف العقلانية وقسمها
لقد استعرضنا سابقًا خصائص الكسور وعملياتها. قدمنا الأرقام المنطقية، وهي مجرد كسور حيث تكون البسط والمتمامات عبارة عن أعداد صحيحة. في هذا الفصل، سوف نتعامل مع الكسور التي يكون البسط والمقامات الخاصة بها كثيرات الحدود. نسمي هذا النوع من التعبير تعبيرًا عقلانيًا.
التعبير العقلاني هو تعبير عن الشكل\(\dfrac{p}{q}\), where \(p\) وهو متعدد الحدود و\(q\) \(q\neq 0\).
فيما يلي بعض الأمثلة على التعبيرات العقلانية:
\[−\dfrac{24}{56} \qquad \dfrac{5x}{12y} \qquad \dfrac{4x+1}{x^2−9} \qquad \dfrac{4x^2+3x−1}{2x−8}\nonumber\]
لاحظ أن التعبير العقلاني الأول المذكور أعلاه\(−\dfrac{24}{56}\)،، هو مجرد كسر. نظرًا لأن الثابت هو كثير الحدود بدرجة صفر، فإن نسبة الثوابتين هي تعبير نسبي، بشرط ألا يكون المقام صفرًا.
سنقوم بنفس العمليات باستخدام التعبيرات النسبية التي أجريناها مع الكسور. سنقوم بتبسيطها وإضافتها وطرحها وضربها وتقسيمها واستخدامها في التطبيقات.
حدد القيم التي لا يتم تعريف التعبير العقلاني لها
إذا كان المقام هو صفر، فإن التعبير العقلاني غير معرف. قد يكون بسط التعبير العقلاني هو 0 - ولكن ليس المقام.
عندما نتعامل مع كسر عددي، فمن السهل تجنب القسمة على الصفر لأننا نستطيع رؤية الرقم في المقام. من أجل تجنب القسمة على الصفر في التعبير العقلاني، يجب ألا نسمح بقيم المتغير التي تجعل المقام صفرًا.
لذا قبل أن نبدأ أي عملية باستخدام تعبير نسبي، نفحصها أولاً لإيجاد القيم التي تجعل المقام صفرًا. بهذه الطريقة، عندما نحل معادلة عقلانية على سبيل المثال، سنعرف ما إذا كانت الحلول الجبرية التي نجدها مسموح بها أم لا.
- عيّن المقام مساويًا للصفر.
- حل المعادلة.
حدد القيمة التي لا يتم تعريف كل تعبير منطقي لها:
أ.\(\dfrac{8a^2b}{3c}\) ب.\(\dfrac{4b−3}{2b+5}\) ج\(\dfrac{x+4}{x^2+5x+6}\).
الحل
لن يتم تعريف التعبير عندما يكون المقام صفرًا.
أ.
\(\begin{array} {ll} &\dfrac{8a^2b}{3c} \\ \begin{array} {l} \text{Set the denominator equal to zero and solve} \\ \text{for the variable.} \end{array} &3c=0 \\ &c=0 \\ &\dfrac{8a^2b}{3c}\text{ is undefined for }c=0 \end{array} \)
ب.
\(\begin{array} {ll} &\dfrac{4b-3}{2b+5} \\ \begin{array} {l} \text{Set the denominator equal to zero and solve} \\ \text{for the variable.} \end{array} &2b+5=0 \\ &2b=-5 \\ &b=-\dfrac{5}{2} \\ & \\ &\dfrac{4b-3}{2b+5} \text{ is undefined for }b=-\dfrac{5}{2} \end{array} \)
ج.
\(\begin{array} {ll} &\dfrac{x+4}{x^2 + 5x + 6} \\ \begin{array} {l} \text{Set the denominator equal to zero and solve } \\ \text{for the variable.} \end{array} &x^2+5x+6=0 \\ &(x+2)(x+3)=0 \\ &x+2=0\text{ or }x+3=0 \\ &x=-2\text{ or }x=-3 \\ & \\ &\dfrac{x+4}{x^2+5x+6}\text{ is undefined for }x=-2\text{ or }x=-3 \end{array} \)
حدد القيمة التي لم يتم تعريف كل تعبير منطقي لها.
أ.\(\dfrac{3y^2}{8x}\) ب.\(\dfrac{8n−5}{3n+1}\) ج.\(\dfrac{a+10}{a^2+4a+3}\)
- إجابة
-
أ.\(x=0\)
ب.\(n=−\dfrac{1}{3}\)
ج.\(a=−1,a=−3\)
حدد القيمة التي لم يتم تعريف كل تعبير منطقي لها.
أ.\(\dfrac{4p}{5q}\) ب.\(\dfrac{y−1}{3y+2}\) ج.\(\dfrac{m−5}{m^2+m−6}\)
- إجابة
-
أ.\(q=0\)
ب.\(y=−\dfrac{2}{3}\)
ج.\(m=2,m=−3\)
تبسيط التعبيرات الكسرية
يعتبر الكسر مبسطًا إذا لم تكن هناك عوامل مشتركة، بخلاف 1، في البسط والمقام. وبالمثل، لا يحتوي التعبير العقلاني المبسط على عوامل مشتركة، بخلاف 1، في البسط والمقام.
يعتبر التعبير العقلاني مبسطًا إذا لم تكن هناك عوامل مشتركة في البسط والمقام.
على سبيل المثال،
\[ \begin{array} {l} \dfrac{x+2}{x+3} \text{ is simplified because there are no common factors of } x+2 \text{ and }x+3. \\ \dfrac{2x}{3x} \text{ is not simplified because x is a common factor of }2x\text{ and }3x. \\ \end{array} \nonumber\]
نحن نستخدم خاصية الكسور المتكافئة لتبسيط الكسور العددية. نعيد ذكرها هنا حيث سنستخدمها أيضًا لتبسيط التعبيرات العقلانية.
إذا\(a\)\(b\)، وما\(c\) هي الأرقام، فأين\(b\neq 0,c\neq 0,\)
\[\text {then } \dfrac{a}{b}=\dfrac{a·c}{b·c} \text{ and } \dfrac{a·c}{b·c}=\dfrac{a}{b}\nonumber\]
لاحظ أنه في خاصية الكسور المتكافئة، لا يُسمح على وجه التحديد بالقيم التي تجعل المقامات صفرًا. نرى\(b\neq 0,c\neq 0\) بوضوح.
لتبسيط التعبيرات الكسرية، نكتب أولاً البسط والمقام في صورة معملية. ثم نزيل العوامل المشتركة باستخدام خاصية الكسور المتكافئة.
كن حذرًا جدًا أثناء إزالة العوامل المشتركة. يتم ضرب العوامل لصنع منتج. يمكنك إزالة عامل من المنتج. لا يمكنك إزالة مصطلح من المجموع.

\(\dfrac{x+5}{x}\)ستكون إزالة\(x\)'s من مثل إلغاء الأحرف\(2\) الموجودة في الكسر\(\dfrac{2+5}{2}!\)
كيفية تبسيط التعبير العقلاني
قم بالتبسيط:\(\dfrac{x^2+5x+6}{x^2+8x+12}\)
الحل
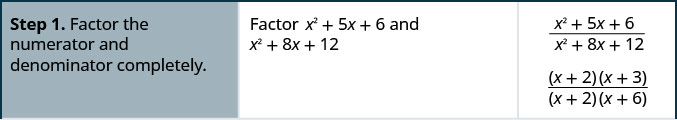

قم بالتبسيط:\(\dfrac{x^2−x−2}{x^2−3x+2}\).
- إجابة
-
\(\dfrac{x+1}{x−1},x\neq 2,x\neq 1\)
قم بالتبسيط:\(\dfrac{x^2−3x−10}{x^2+x−2}\).
- إجابة
-
\(\dfrac{x−5}{x−1},x\neq −2,x\neq 1\)
نلخص الآن الخطوات التي يجب اتباعها لتبسيط التعبيرات العقلانية.
- ضع البسط والمقام في الاعتبار تمامًا.
- قم بالتبسيط من خلال تقسيم العوامل المشتركة.
عادة، نترك التعبير العقلاني المبسط في شكل عامل. بهذه الطريقة، من السهل التحقق من أننا أزلنا جميع العوامل المشتركة.
سنستخدم الطرق التي تعلمناها لتحليل كثيرات الحدود في البسط والمقامات في الأمثلة التالية.
في كل مرة نكتب فيها تعبيرًا منطقيًا، يجب أن نصدر بيانًا لا يسمح بالقيم التي من شأنها أن تجعل المقام صفرًا. ومع ذلك، دعونا نركز على العمل المطروح، سنحذف كتابته في الأمثلة.
قم بالتبسيط:\(\dfrac{3a^2−12ab+12b^2}{6a^2−24b^2}\).
الحل
\(\begin{array} {ll} &\dfrac{3a^2−12ab+12b^2}{6a^2−24b^2} \\ & \\ & \\ \begin{array} {l} \text{Factor the numerator and denominator,} \\ \text{first factoring out the GCF.} \end{array} &\dfrac{3(a^2−4ab+4b^2)}{6(a^2−4b^2)} \\ & \\ &\dfrac{3(a−2b)(a−2b)}{6(a+2b)(a−2b)} \\ & \\ \text{Remove the common factors of }a−2b\text{ and }3. &\dfrac{\cancel{3}(a−2b)\cancel{(a−2b)}}{\cancel{3}·2(a+2b)\cancel{(a−2b)}} \\ &\dfrac{a−2b}{2(a+2b)} \end{array} \)
قم بالتبسيط:\(\dfrac{2x^2−12xy+18y^2}{3x^2−27y^2}\).
- إجابة
-
\(\dfrac{2(x−3y)}{3(x+3y)}\)
قم بالتبسيط:\(\dfrac{5x^2−30xy+25y^2}{2x^2−50y^2}\).
- إجابة
-
\(\dfrac{5(x−y)}{2(x+5y)}\)
سنرى الآن كيفية تبسيط التعبير العقلاني الذي يحتوي البسط والمقام على عوامل معاكسة. لقد قدمنا سابقًا ترميزًا معاكسًا: عكس\(a\) هو\(−a\) و\(−a=−1·a\).
الكسر العددي، على سبيل المثال،\(\dfrac{7}{−7}\) يبسط إلى\(−1\). نحن ندرك أيضًا أن البسط والمقام متضادان.
يتم أيضًا تبسيط الكسر\(\dfrac{a}{−a}\)، الذي يكون بسطه ومقامه متضادان، إلى\(−1\).
\[\begin{array} {ll} \text{Let’s look at the expression }b−a. &b−a \\ \text{Rewrite.} &−a+b \\ \text{Factor out }–1. &−1(a−b) \nonumber\end{array} \]
هذا يخبرنا أن هذا\(b−a\) هو عكس ذلك\(a−b\).
بشكل عام، يمكننا كتابة عكس\(a−b\) as\(b−a\). لذا فإن التعبير العقلاني\(\dfrac{a−b}{b−a}\) يبسط إلى\(−1\).
على العكس من\(a−b\) ذلك\(b−a\).
\[\dfrac{a−b}{b−a}=−1 \quad a\neq b\nonumber\]
تعبير وانقسامه المعاكس إلى\(−1\).
سنستخدم هذه الخاصية لتبسيط التعبيرات العقلانية التي تحتوي على أضداد في البسط والمقامات. احرص على عدم العلاج\(a+b\)\(b+a\) وكأضداد. تذكر أنه بالإضافة إلى ذلك، لا يهم الترتيب\(a+b=b+a\). لذا إذا\(a\neq −b\)، إذن\(\dfrac{a+b}{b+a}=1\).
قم بالتبسيط:\(\dfrac{x^2−4x−32}{64−x^2}\)
الحل
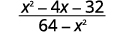 |
|
| ضع في اعتبارك البسط والمقام. | 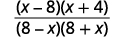 |
| تعرف على العوامل المضادة. | 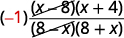 |
| قم بالتبسيط. | 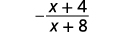 |
قم بالتبسيط:\(\dfrac{x^2−4x−5}{25−x^2}\)
- إجابة
-
\(−\dfrac{x+1}{x+5}\)
قم بالتبسيط:\(\dfrac{x^2+x−2}{1−x^2}\).
- إجابة
-
\(−\dfrac{x+2}{x+1}\)
ضرب التعبيرات الكسرية
لضرب المقادير الكسرية، نقوم بما فعلناه بالكسور العددية. نضرب البسط ونضرب القواسم. ثم، إذا كانت هناك أي عوامل مشتركة، فإننا نزيلها لتبسيط النتيجة.
إذا كانت\(p\)\(q\)،\(r\)،، وما\(s\) زالت كثيرة الحدود حيث\(q\neq 0\)\(s\neq 0\)، إذن
\[\dfrac{p}{q}·\dfrac{r}{s}=\dfrac{pr}{qs}\nonumber\]
لضرب التعبيرات العقلانية، اضرب البسط واضرب المقامات.
تذكر أننا سنفترض خلال هذا الفصل أن جميع القيم العددية التي تجعل المقام صفرًا مستبعدة. لن نكتب القيود الخاصة بكل تعبير عقلاني، ولكن ضع في اعتبارك أن المقام لا يمكن أن يكون صفرًا أبدًا. لذا في هذا المثال التالي\(x\neq 0\)،\(x\neq 3\)، و\(x\neq 4.\)
قم بالتبسيط:\(\dfrac{2x}{x^2−7x+12}·\dfrac{x^2−9}{6x^2}\).
الحل
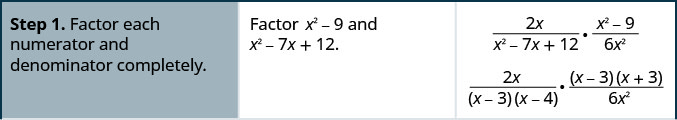


قم بالتبسيط:\(\dfrac{5x}{x^2+5x+6}·\dfrac{x^2−4}{10x}\).
- إجابة
-
\(\dfrac{x−2}{2(x+3)}\)
قم بالتبسيط:\(\dfrac{9x^2}{x^2+11x+30}·\dfrac{x^2−36}{3x^2}\).
- إجابة
-
\(\dfrac{3(x−6)}{x+5}\)
- ضع في اعتبارك كل بسط ومقام بالكامل.
- اضرب البسط والمقامات.
- قم بالتبسيط من خلال تقسيم العوامل المشتركة.
اضرب:\(\dfrac{3a^2−8a−3}{a^2−25}·\dfrac{a^2+10a+25}{3a^2−14a−5}\).
الحل
\(\begin{array} {ll} &\dfrac{3a^2−8a−3}{a^2−25}·\dfrac{a^2+10a+25}{3a^2−14a−5} \\ & \\ \begin{array} {ll} \text{Factor the numerators and denominators} \\ \text{and then multiply.} \end{array} &\dfrac{(3a+1)(a−3)(a+5)(a+5)}{(a−5)(a+5)(3a+1)(a−5)} \\ & \\ \begin{array} {l} \text{Simplify by dividing out} \\ \text{common factors.} \end{array} &\dfrac{\cancel{(3a+1)}(a−3)\cancel{(a+5)}(a+5)}{(a−5)\cancel{(a+5)}\cancel{(3a+1)}(a−5)} \\ & \\ \text{Simplify.} &\dfrac{(a−3)(a+5)}{(a−5)(a−5)} \\ & \\ \text{Rewrite }(a−5)(a−5)\text{ using an exponent.} &\dfrac{(a−3)(a+5)}{(a−5)^2} \end{array}\)
قم بالتبسيط:\(\dfrac{2x^2+5x−12}{x^2−16}·\dfrac{x^2−8x+16}{2x^2−13x+15}\).
- إجابة
-
\(\dfrac{x−4}{x−5}\)
قم بالتبسيط:\(\dfrac{4b^2+7b−2}{1−b^2}·\dfrac{b^2−2b+1}{4b^2+15b−4}\).
- إجابة
-
\(−\dfrac{(b+2)(b−1)}{(1+b)(b+4)}\)
قسمة التعبيرات الكسرية
تمامًا كما فعلنا مع الكسور العددية، لقسمة التعبيرات الكسرية، نضرب الكسر الأول في مقلوب الثاني.
إذا كانت\(p\)\(q\)،\(r\)،، وما زالت\(s\) كثيرة الحدود حيث\(q\neq 0\)،\(r\neq 0\)،\(s\neq 0\)، إذن
\[\dfrac{p}{q}÷\dfrac{r}{s}=\dfrac{p}{q}·\dfrac{s}{r}\nonumber\]
لتقسيم التعبيرات العقلانية، اضرب الكسر الأول في مقلوب الثاني.
بمجرد إعادة كتابة القسمة كضرب للتعبير الأول في مقلوب الثاني، نقوم بعد ذلك بحساب كل شيء والبحث عن العوامل المشتركة.
قسّم:\(\dfrac{p^3+q^3}{2p^2+2pq+2q^2}÷\dfrac{p^2−q^2}{6}\).
الحل




قم بالتبسيط:\(\dfrac{x^3−8}{3x^2−6x+12}÷\dfrac{x^2-4}{6}\).
- إجابة
-
\(\dfrac{2(x^2+2x+4)}{(x+2)(x^2−2x+4)}\)
قم بالتبسيط:\(\dfrac{2z^2}{z^2−1}÷\dfrac{z^3−z^2+z}{z^3+1}\).
- إجابة
-
\(\dfrac{2z}{z−1}\)
- أعد كتابة القسمة كمنتج للتعبير العقلاني الأول ومقابل الثاني.
- ضع البسط والمقامات في الاعتبار بشكل كامل.
- اضرب البسط والمقامات معًا.
- قم بالتبسيط من خلال تقسيم العوامل المشتركة.
تذكر من استخدام لغة الجبر أن الكسر المركب هو كسر يحتوي على كسر في البسط أو المقام أو كليهما. تذكر أيضًا أن شريط الكسر يعني القسمة. الكسر المركب هو طريقة أخرى لكتابة قسمة كسرين.
قسّم:\(\dfrac{\dfrac{6x^2−7x+2}{4x−8}}{\dfrac{2x^2−7x+3}{x^2−5x+6}}\).
الحل
\(\begin{array} {ll} &\dfrac{\dfrac{6x^2−7x+2}{4x−8}}{\dfrac{2x^2−7x+3}{x^2−5x+6}} \\ & \\ \text{Rewrite with a division sign.} &\dfrac{6x^2−7x+2}{4x−8}÷\dfrac{2x^2−7x+3}{x^2−5x+6} \\ & \\ \begin{array} {l} \text{Rewrite as product of first times reciprocal} \\ \text{of second.} \end{array} &\dfrac{6x^2−7x+2}{4x−8}·\dfrac{x^2−5x+6}{2x^2−7x+3} \\ & \\ \begin{array} {l} \text{Factor the numerators and the} \\ \text{denominators, and then multiply.} \end{array} &\dfrac{(2x−1)(3x−2)(x−2)(x−3)}{4(x−2)(2x−1)(x−3)} \\ & \\ \text{Simplify by dividing out common factors.} &\dfrac{\cancel{(2x−1)}(3x−2)\cancel{(x−2)}\cancel{(x−3)}}{4\cancel{(x−2)}\cancel{(2x−1)}\cancel{(x−3)}} \\ \text{Simplify.} &\dfrac{3x−2}{4} \end{array}\)
قم بالتبسيط:\(\dfrac{\dfrac{3x^2+7x+2}{4x+24}}{\dfrac{3x^2−14x−5}{x^2+x−30}}\).
- إجابة
-
\(\dfrac{x+2}{4}\)
قم بالتبسيط:\(\dfrac{\dfrac{y^2−36}{2y^2+11y−6}}{\dfrac{2y^2−2y−60}{8y−4}}\).
- إجابة
-
\(\dfrac{2}{y+5}\)
إذا كان لدينا أكثر من تعبيرين منطقيين للعمل بهما، فإننا لا نزال نتبع نفس الإجراء. ستكون الخطوة الأولى هي إعادة كتابة أي قسمة كضرب في المعاملة بالمثل. ثم نأخذ في الاعتبار ونضرب.
نفذ العمليات المشار إليها:\(\dfrac{3x−6}{4x−4}·\dfrac{x^2+2x−3}{x^2−3x−10}÷\dfrac{2x+12}{8x+16}\).
الحل
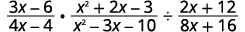 |
|
| أعد كتابة القسمة في صورة ضرب في المقلوب. |
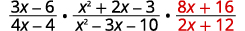 |
| ضع في اعتبارك البسط والقواسم. | 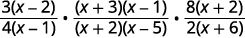 |
| اضرب الكسور. سيساعد جلب الثوابت إلى الأمام عند إزالة العوامل المشتركة. |
|
| قم بالتبسيط من خلال تقسيم العوامل المشتركة. | 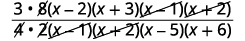 |
| قم بالتبسيط. | 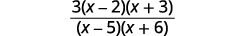 |
نفذ العمليات المشار إليها:\(\dfrac{4m+4}{3m−15}·\dfrac{m^2−3m−10}{m^2−4m−32}÷\dfrac{12m−36}{6m−48}\).
- إجابة
-
\(\dfrac{2(m+1)(m+2)}{3(m+4)(m−3)}\)
نفذ العمليات المشار إليها:\(\dfrac{2n^2+10n}{n−1}÷\dfrac{n^2+10n+24}{n^2+8n−9}·\dfrac{n+4}{8n^2+12n}\).
- إجابة
-
\(\dfrac{(n+5)(n+9)}{2(n+6)(2n+3)}\)
ضرب الدوال الكسرية وقسمتها
بدأنا هذا القسم بالقول إن التعبير العقلاني هو تعبير عن الشكل\(\dfrac{p}{q}\)، حيث p و q هما كثيرات الحدود و\(q\neq 0\). وبالمثل، نقوم بتعريف الدالة الكسرية كدالة للشكل\(R(x)=\dfrac{p(x)}{q(x)}\) حيث\(p(x)\)\(q(x)\) وهي دوال كثيرة الحدود وليست صفرًا.\(q(x)\)
الدالة العقلانية هي دالة للنموذج
\[R(x)=\dfrac{p(x)}{q(x)}\nonumber\]
أين\(p(x)\)\(q(x)\) وهي دوال كثيرة الحدود\(q(x)\) وليست صفرية.
مجال الدالة النسبية هو جميع الأرقام الحقيقية باستثناء تلك القيم التي قد تتسبب في القسمة على الصفر. يجب علينا القضاء على أي قيم تصنع\(q(x)=0\).
- عيّن المقام مساويًا للصفر.
- حل المعادلة.
- النطاق هو جميع الأرقام الحقيقية باستثناء القيم الموجودة في الخطوة 2.
ابحث عن نطاق\(R(x)=\dfrac{2x^2−14x}{4x^2−16x−48}\).
الحل
سيكون المجال عبارة عن جميع الأرقام الحقيقية باستثناء تلك القيم التي تجعل المقام صفرًا. سنحدد المقام الذي يساوي الصفر، ونحل هذه المعادلة، ثم نستبعد هذه القيم من المجال.
\(\begin{array} {ll} \text{Set the denominator to zero.} &4x^2−16x−48=0 \\ \text{Factor, first factor out the GCF.} &4(x^2−4x−12)=0 \\ &4(x−6)(x+2)=0 \\ \text{Use the Zero Product Property.} &4\neq 0\quad x−6=0\quad x+2=0 \\ \text{Solve.} &\hspace{24mm}x=6\qquad x=−2 \\ &\text{The domain of }R(x)\text{ is all real numbers} \\ &\text{where }x\neq 6\text{ and }x\neq −2 \end{array}\).
ابحث عن نطاق\(R(x)=\dfrac{2x^2−10x}{4x^2−16x−20}\).
- إجابة
-
مجال\(R(x)\) كل الأرقام الحقيقية أين\(x\neq 5\) و\(x\neq −1\).
ابحث عن نطاق\(R(x)=\dfrac{4x^2−16x}{8x^2−16x−64}\).
- إجابة
-
مجال\(R(x)\) كل الأرقام الحقيقية أين\(x\neq 4\) و\(x\neq −2\).
لضرب الدوال الكسرية، نضرب المقادير الكسرية الناتجة على الجانب الأيمن من المعادلة باستخدام نفس الأساليب التي استخدمناها لضرب التعبيرات الكسرية.
ابحث عن\(R(x)=f(x)·g(x)\) المكان\(f(x)=\dfrac{2x−6}{x^2−8x+15}\) و\(g(x)=\dfrac{x^2−25}{2x+10}\).
الحل
\(\begin{array} {ll} &R(x)=f(x)·g(x) \\ & \\ &R(x)=\dfrac{2x−6}{x^2−8x+15}·\dfrac{x^2−25}{2x+10} \\ & \\ \text{Factor each numerator and denominator.} &R(x)=\dfrac{2(x−3)}{(x−3)(x−5)}·\dfrac{(x−5)(x+5)}{2(x+5)} \\ & \\ \text{Multiply the numerators and denominators.} &R(x)=\dfrac{2(x−3)(x−5)(x+5)}{2(x−3)(x−5)(x+5)} \\ & \\ \text{Remove common factors.} &R(x)=\dfrac{\cancel{2}\cancel{(x−3)}\cancel{(x−5)}\cancel{(x+5)}}{\cancel{2}\cancel{(x−3)}\cancel{(x−5)}\cancel{(x+5)}} \\ & \\ \text{Simplify.} &R(x)=1 \end{array}\)
ابحث عن\(R(x)=f(x)·g(x)\) المكان\(f(x)=\dfrac{3x−21}{x^2−9x+14}\) و\(g(x)=\dfrac{2x^2−8}{3x+6}\).
- إجابة
-
\(R(x)=2\)
ابحث عن\(R(x)=f(x)·g(x)\) المكان\(f(x)=\dfrac{x^2−x}{3x^2+27x−30}\) و\(g(x)=\dfrac{x^2−100}{x^2−10x}\).
- إجابة
-
\(R(x)=\dfrac{1}{3}\)
لتقسيم الدوال الكسرية، نقسم التعبيرات الكسرية الناتجة على الجانب الأيمن من المعادلة باستخدام نفس الأساليب التي استخدمناها لتقسيم التعبيرات الكسرية.
ابحث عن\(R(x)=\dfrac{f(x)}{g(x)}\) المكان\(f(x)=\dfrac{3x^2}{x^2−4x}\) و\(g(x)=\dfrac{9x^2−45x}{x^2−7x+10}\).
الحل
\(\begin{array} {ll} &R(x)=\dfrac{f(x)}{g(x)} \\ \text{Substitute in the functions }f(x),\space g(x). &R(x)=\dfrac{\dfrac{3x^2}{x^2−4x}}{\dfrac{9x^2−45x}{x^2−7x+10}} \\ & \\ \begin{array} {l} \text{Rewrite the division as the product of} \\ f(x)\text{ and the reciprocal of }g(x). \end{array} &R(x)=\dfrac{3x^2}{x^2−4x}·\dfrac{x^2−7x+10}{9x^2−45x} \\ & \\ \begin{array} {l} \text{Factor the numerators and denominators} \\ \text{and then multiply.} \end{array} &R(x)=\dfrac{3·x·x·(x−5)(x−2)}{x(x−4)·3·3·x·(x−5)} \\ & \\ \text{Simplify by dividing out common factors.} &R(x)=\dfrac{\cancel{3}·\cancel{x}·\cancel{x}\cancel{(x−5)}(x−2)}{\cancel{x}(x−4)·\cancel{3}·3·\cancel{x}\cancel{(x−5)}} \\ & \\ &R(x)=\dfrac{x−2}{3(x−4)} \end{array}\)
ابحث عن\(R(x)=\dfrac{f(x)}{g(x)}\) المكان\(f(x)=\dfrac{2x^2}{x^2−8x}\) و\(g(x)=\dfrac{8x^2+24x}{x^2+x−6}\).
- إجابة
-
\(R(x)=\dfrac{x−2}{4(x−8)}\)
ابحث عن\(R(x)=\dfrac{f(x)}{g(x)}\) المكان\(f(x)=\dfrac{15x^2}{3x^2+33x}\) و\(g(x)=\dfrac{5x−5}{x^2+9x−22}\).
- إجابة
-
\(R(x)=\dfrac{x(x−2)}{x−1}\)
المفاهيم الرئيسية
- حدد القيم التي لا يتم تعريف التعبير العقلاني لها.
- عيّن المقام مساويًا للصفر.
- حل المعادلة.
- خاصية الكسور المتكافئة
إذا كانت الأرقام\(a\)\(b\)، وما\(c\) هي\(b\neq 0\)، وأين\(c\neq 0\)، ثم،
\(\quad\dfrac{a}{b}=\dfrac{a·c}{b·c}\) و\(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\) - كيفية تبسيط التعبير العقلاني.
- ضع البسط والمقام في الاعتبار تمامًا.
- قم بالتبسيط من خلال تقسيم العوامل المشتركة.
- الأضداد في التعبير
العقلاني نقيض\(a−b\) ذلك\(b−a\).
\(\quad\dfrac{a−b}{b−a}=−1 \qquad a\neq b\)
تعبير وانقسامه المعاكس إلى\(−1\). - ضرب التعبيرات الكسرية
إذا كانت\(p\)\(q\)\(r\)\(s\) وكثيرات الحدود\(q\neq 0\)\(s\neq 0\)، ثم
\(\quad\dfrac{p}{q}·\dfrac{r}{s}=\dfrac{pr}{qs}\) - كيفية ضرب التعبيرات العقلانية.
- ضع في اعتبارك كل بسط ومقام بالكامل.
- اضرب البسط والمقامات.
- قم بالتبسيط من خلال تقسيم العوامل المشتركة.
- قسمة التعبيرات الكسرية
إذا كانت\(s\) وكثيرات الحدود\(p\)،\(q\) وإذا\(q\neq 0\)\(r\neq 0\)،\(s\neq 0\)، ثم\(r\)
\(\quad\dfrac{p}{q}÷\dfrac{r}{s}=\dfrac{p}{q}·\dfrac{s}{r}\) - كيفية تقسيم التعبيرات العقلانية.
- أعد كتابة القسمة كمنتج للتعبير العقلاني الأول ومقابل الثاني.
- ضع البسط والمقامات في الاعتبار بشكل كامل.
- اضرب البسط والمقامات معًا.
- قم بالتبسيط من خلال تقسيم العوامل المشتركة.
- كيفية تحديد مجال الدالة الكسرية.
- عيّن المقام مساويًا للصفر.
- حل المعادلة.
- النطاق هو جميع الأرقام الحقيقية باستثناء القيم الموجودة في الخطوة 2.
مسرد المصطلحات
- تعبير عقلاني
- التعبير العقلاني هو تعبير عن الشكل وأين\(\dfrac{p}{q}\)\(p\)\(q\) وكثيرات الحدود و\(q\neq 0\).
- تعبير عقلاني مبسط
- لا يحتوي التعبير العقلاني المبسط على عوامل مشتركة\(1\)، بخلاف البسط والمقام.
- دالة عقلانية
- الدالة الكسرية هي دالة في الشكل\(R(x)=\dfrac{p(x)}{q(x)}\) حيث\(p(x)\)\(q(x)\) تكون دوال كثيرة الحدود وليست صفرًا.\(q(x)\)


