6.5: الإستراتيجية العامة لتحليل التعبيرات كثيرة الحدود

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

• تعرف على الطريقة المناسبة واستخدمها لتحليل كثير الحدود تمامًا

تعرف على الطريقة المناسبة واستخدمها لتحليل كثير الحدود تمامًا

لقد تعرفت الآن على جميع طرق التخصيم التي ستحتاجها في هذه الدورة. يلخص المخطط التالي جميع طرق العوملة التي قمنا بتغطيتها، ويحدد الإستراتيجية التي يجب عليك استخدامها عند حساب كثيرات الحدود.

الإستراتيجية العامة لتخصيم كثيرات الحدود

استخدم إستراتيجية عامة لتحليل كثيرات الحدود.

1. هل هناك عامل مشترك أكبر؟
   ضع في اعتبارك ذلك.
2. هل كثير الحدود عبارة عن معادلة ذات حدين أو ثلاثية أو أكثر من ثلاثة حدود؟
   إذا كانت عبارة عن معادلة ذات حدين:
   • هل هو مبلغ؟
     من المربعات؟ لا تؤخذ مجاميع المربعات في الاعتبار.
     من المكعبات؟ استخدم نمط مجموع المكعبات.
   • هل هذا فرق؟
     من المربعات؟ عامل كمنتج للمقارنات.
     من المكعبات؟ استخدم الفرق بين نمط المكعبات.
   إذا كانت ثلاثية الحدود:
   • هل هو من النموذج$x^2+bx+c$؟ التراجع عن الفويل.
   • هل هو من النموذج$ax^2+bx+c$؟
     إذا كانت a و c عبارة عن مربعات، فتحقق مما إذا كانت تناسب نمط المربع الثلاثي.
     استخدم طريقة التجربة والخطأ أو «$ac$».
   إذا كان يحتوي على أكثر من ثلاثة فصول:
   • استخدم طريقة التجميع.
3. تحقق.
   هل يتم أخذها في الاعتبار بالكامل؟
   هل تتضاعف العوامل مرة أخرى في كثير الحدود الأصلي؟

تذكر أن تعدد الحدود يؤخذ في الاعتبار تمامًا إذا كانت عوامله أساسية بخلاف القيم الأحادية!

مثال$\PageIndex{1}$

عامل بالكامل:$7x^3−21x^2−70x$.

الحل

$\begin{array} {ll} {7x^3−21x^2−70x} & \\ \text{Is there a GCF? Yes, }7x. & \\ \text{Factor out the GCF.} &7x(x^2−3x−10) \\ \text{In the parentheses, is it a binomial, trinomial,} & \\ \text{or are there more terms?} & \\ \text{Trinomial with leading coefficient 1.} & \\ \text{“Undo” FOIL.} &7x(x\hspace{8mm})(x\hspace{8mm}) \\ &7x(x+2)(x−5) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Neither binomial can be factored.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ & \\ & \\ \hspace{15mm}7x(x+2)(x−5) & \\ \hspace{10mm}7x(x^2−5x+2x−10) & \\ \hspace{15mm}7x(x^2−3x−10) & \\ \hspace{13mm}7x^3−21x^2−70x\checkmark & \end{array}$

جرب ذلك$\PageIndex{1}$

عامل بالكامل:$8y^3+16y^2−24y$.

إجابة

$8y(y−1)(y+3)$

جرب ذلك$\PageIndex{2}$

عامل بالكامل:$5y^3−15y^2−270y$.

إجابة

$5y(y−9)(y+6)$

كن حذرًا عندما يُطلب منك وضع معادلة ذات حدين نظرًا لوجود العديد من الخيارات!

مثال$\PageIndex{2}$

عامل بالكامل:$24y^2−150$

الحل

$\begin{array} {ll} &24y^2−150 \\ \text{Is there a GCF? Yes, }6. & \\ \text{Factor out the GCF.} &6(4y^2−25) \\ \text{In the parentheses, is it a binomial, trinomial} & \\ \text{or are there more than three terms? Binomial.} & \\ \text{Is it a sum? No.} & \\ \text{Is it a difference? Of squares or cubes? Yes, squares.} &6((2y)^2−(5)^2) \\ \text{Write as a product of conjugates.} &6(2y−5)(2y+5) \\ & \\ & \\ \hspace{5mm}\text{Is the expression factored completely?} & \\ \hspace{5mm}\text{Neither binomial can be factored.} & \\ \text{Check:} & \\ & \\ & \\ \hspace{5mm}\text{Multiply.} & \\ & \\ \hspace{15mm}6(2y−5)(2y+5) & \\ & \\ \hspace{18mm}6(4y^2−25) & \\ \hspace{18mm}24y^2−150\checkmark \end{array}$

جرب ذلك$\PageIndex{3}$

عامل بالكامل:$16x^3−36x$.

إجابة

$4x(2x−3)(2x+3)$

جرب ذلك$\PageIndex{4}$

عامل بالكامل:$27y^2−48$.

إجابة

$3(3y−4)(3y+4)$

يمكن أخذ المثال التالي بعين الاعتبار باستخدام عدة طرق. التعرف على نمط المربعات الثلاثية سيجعل عملك أسهل.

مثال$\PageIndex{3}$

عامل بالكامل:$4a^2−12ab+9b^2$.

الحل

$\begin{array} {ll} &4a^2−12ab+9b^2 \\ \text{Is there a GCF? No.} & \\ \text{Is it a binomial, trinomial, or are there more terms?} & \\ \text{Trinomial with }a\neq 1.\text{ But the first term is a perfect square.} \\ \text{Is the last term a perfect square? Yes.} &(2a)^2−12ab+(3b)^2 \\ \text{Does it fit the pattern, }a^2−2ab+b^2?\text{ Yes.} &(2a)^2 −12ab+ (3b)^2 \\ &\hspace{7mm} {\,}^{\searrow}{\,}_{−2(2a)(3b)}{\,}^{\swarrow}\\ \text{Write it as a square.} &(2a−3b)^2 \\ & \\ & \\ \quad\text{Is the expression factored completely? Yes.} & \\ \quad\text{The binomial cannot be factored.} & \\ \text{Check your answer.} \\ & \\ & \\ \quad\text{Multiply.} & \\ \hspace{30mm}(2a−3b)^2 \\ \hspace{20mm} (2a)^2−2·2a·3b+(3b)^2 \\ \hspace{24mm}4a^2−12ab+9b^2\checkmark & \end{array}$

جرب ذلك$\PageIndex{5}$

عامل بالكامل:$4x^2+20xy+25y^2$.

إجابة

$(2x+5y)^2$

جرب ذلك$\PageIndex{6}$

عامل بالكامل:$9x^2−24xy+16y^2$.

إجابة

$(3x−4y)^2$

تذكر أن مجموع المربعات لا يأخذ بعين الاعتبار، ولكن مجموع المكعبات يؤثر!

مثال$\PageIndex{4}$

عامل بالكامل$12x^3y^2+75xy^2$.

الحل

$\begin{array} {ll} &12x^3y^2+75xy^2 \\ \text{Is there a GCF? Yes, }3xy^2. & \\ \text{Factor out the GCF.} &3xy^2(4x^2+25) \\ \text{In the parentheses, is it a binomial, trinomial, or are} & \\ \text{there more than three terms? Binomial.} & \\ & \\ \text{Is it a sum? Of squares? Yes.} &\text{Sums of squares are prime.} \\ & \\ & \\ \quad\text{Is the expression factored completely? Yes.} & \\ \text{Check:} & \\ & \\ & \\ \quad\text{Multiply.} & \\ \hspace{15mm}3xy^2(4x^2+25) & \\ \hspace{14mm}12x^3y^2+75xy^2\checkmark \end{array}$

جرب ذلك$\PageIndex{7}$

عامل بالكامل:$50x^3y+72xy$.

إجابة

$2xy(25x^2+36)$

جرب ذلك$\PageIndex{8}$

عامل بالكامل:$27xy^3+48xy$.

إجابة

$3xy(9y^2+16)$

عند استخدام نمط مجموع المكعبات أو اختلافها، يجب توخي الحذر عند استخدام العلامات.

مثال$\PageIndex{5}$

عامل بالكامل:$24x^3+81y^3$.

الحل

هل هناك GCF؟ نعم، 3.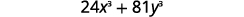
ضع في اعتبارك ذلك.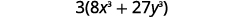
بين القوسين، هل هو عبارة عن معادلة ذات حدين، أو ثلاثية، أو هل هناك أكثر من ثلاثة حدود؟ معادلة ذات حدين.
هل هو مبلغ أم فرق؟ مجموع.
من المربعات أو المكعبات؟ مجموع المكعبات.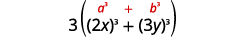
اكتبها باستخدام نمط مجموع المكعبات.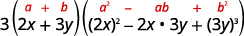
هل التعبير يؤخذ في الاعتبار بشكل كامل؟ نعم.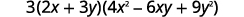
تحقق عن طريق الضرب.

جرب ذلك$\PageIndex{9}$

عامل بالكامل:$250m^3+432n^3$.

إجابة

$2(5m+6n)(25m^2−30mn+36n^2)$

جرب ذلك$\PageIndex{10}$

عامل بالكامل:$2p^3+54q^3$.

إجابة

$2(p+3q)(p^2−3pq+9q^2)$

مثال$\PageIndex{6}$

عامل بالكامل:$3x^5y−48xy$.

الحل

$\begin{array} {ll} &3x^5y−48xy \\ \text{Is there a GCF? Factor out }3xy &3xy(x^4−16) \\ \begin{array} {l} \text{Is the binomial a sum or difference? Of squares or cubes?} \\ \text{Write it as a difference of squares.} \end{array} &3xy\left((x^2)^2−(4)2\right) \\ \text{Factor it as a product of conjugates} &3xy(x^2−4)(x^2+4) \\ \text{The first binomial is again a difference of squares.} &3xy\left((x)^2−(2)^2\right)(x^2+4) \\ \text{Factor it as a product of conjugates.} &3xy(x−2)(x+2)(x^2+4) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ 3xy(x−2)(x+2)(x^2+4) & \\ 3xy(x^2−4)(x^2+4) & \\ 3xy(x^4−16) & \\ 3x^5y−48xy\checkmark & \end{array}$

جرب ذلك$\PageIndex{11}$

عامل بالكامل:$4a^5b−64ab$.

إجابة

$4ab(a^2+4)(a−2)(a+2)$

جرب ذلك$\PageIndex{12}$

عامل بالكامل:$7xy^5−7xy$.

إجابة

$7xy(y^2+1)(y−1)(y+1)$

مثال$\PageIndex{7}$

عامل بالكامل:$4x^2+8bx−4ax−8ab$.

الحل

$\begin{array} {ll} &4x^2+8bx−4ax−8ab \\ \text{Is there a GCF? Factor out the GCF, }4. &4(x^2+2bx−ax−2ab) \\ \text{There are four terms. Use grouping.} &4[x(x+2b)−a(x+2b)]4(x+2b)(x−a) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{25mm}4(x+2b)(x−a) & \\ \hspace{20mm} 4(x^2−ax+2bx−2ab) & \\ \hspace{20mm}4x^2+8bx−4ax−8ab\checkmark \end{array}$

جرب ذلك$\PageIndex{13}$

عامل بالكامل:$6x^2−12xc+6bx−12bc$.

إجابة

$6(x+b)(x−2c)$

جرب ذلك$\PageIndex{14}$

عامل بالكامل:$16x^2+24xy−4x−6y$.

إجابة

$2(4x−1)(2x+3y)$

إن الحصول على GCF الكامل في الخطوة الأولى سيجعل عملك دائمًا أسهل.

مثال$\PageIndex{8}$

عامل بالكامل:$40x^2y+44xy−24y$.

الحل

$\begin{array} {ll} &40x^2y+44xy−24y \\ \text{Is there a GCF? Factor out the GCF, }4y. &4y(10x^2+11x−6) \\ \text{Factor the trinomial with }a\neq 1. &4y(10x^2+11x−6) \\ &4y(5x−2)(2x+3) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{25mm}4y(5x−2)(2x+3) & \\ \hspace{24mm}4y(10x^2+11x−6) & \\ \hspace{22mm}40x^2y+44xy−24y\checkmark \end{array}$

جرب ذلك$\PageIndex{15}$

عامل بالكامل:$4p^2q−16pq+12q$.

إجابة

$4q(p−3)(p−1)$

جرب ذلك$\PageIndex{16}$

عامل بالكامل:$6pq^2−9pq−6p$.

إجابة

$3p(2q+1)(q−2)$

عندما نأخذ في الاعتبار تعدد الحدود بأربعة مصطلحات، غالبًا ما قمنا بتقسيمه إلى مجموعتين من فترتين. تذكر أنه يمكننا أيضًا فصله إلى مصطلح ثلاثي ثم مصطلح واحد.

مثال$\PageIndex{9}$

عامل بالكامل:$9x^2−12xy+4y^2−49$.

الحل

$\begin{array} {ll} &9x^2−12xy+4y^2−49 \\ \text{Is there a GCF? No.} & \\ \begin{array} {l} \text{With more than 3 terms, use grouping. Last 2 terms} \\ \text{have no GCF. Try grouping first 3 terms.} \end{array} &9x^2−12xy+4y^2−49 \\ \begin{array} {l} \text{Factor the trinomial with }a\neq 1. \text{ But the first term is a} \\ \text{perfect square.} \end{array} & \\ \text{Is the last term of the trinomial a perfect square? Yes.} &(3x)^2−12xy+(2y)^2−49 \\ \text{Does the trinomial fit the pattern, }a^2−2ab+b^2? \text{ Yes.} &(3x)^2 −12xy+ (2y)^2−49 \\ &\hspace{7mm} {\,}^{\searrow}{\,}_{−2(3x)(2y))}{\,}^{\swarrow} \\ \text{Write the trinomial as a square.} &(3x−2y)^2−49 \\ \begin{array} {ll} \text{Is this binomial a sum or difference? Of squares or} \\ \text{cubes? Write it as a difference of squares.} \end{array} &(3x−2y)^2−72 \\ \text{Write it as a product of conjugates.} &((3x−2y)−7)((3x−2y)+7) \\ &(3x−2y−7)(3x−2y+7) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{23mm}(3x−2y−7)(3x−2y+7) & \\ \hspace{10mm}9x^2−6xy−21x−6xy+4y^2+14y+21x−14y−49 \qquad & \\ \hspace{25mm}9x^2−12xy+4y^2−49\checkmark & \end{array}$

جرب ذلك$\PageIndex{17}$

عامل بالكامل:$4x^2−12xy+9y^2−25$.

إجابة

$(2x−3y−5)(2x−3y+5)$

جرب ذلك$\PageIndex{18}$

عامل بالكامل:$16x^2−24xy+9y^2−64$.

إجابة

$(4x−3y−8)(4x−3y+8)$

المفاهيم الرئيسية

• كيفية استخدام استراتيجية عامة لتحليل كثيرات الحدود.
  1. هل هناك عامل مشترك أكبر؟
     ضع في اعتبارك ذلك.
  2. هل كثير الحدود عبارة عن معادلة ذات حدين أو ثلاثية أو أكثر من ثلاثة حدود؟
     إذا كانت معادلة ذات حدين:
     هل هي عبارة عن مبلغ؟
     من المربعات؟ لا تؤخذ مجاميع المربعات في الاعتبار.
     من المكعبات؟ استخدم نمط مجموع المكعبات.
     هل هذا فرق؟
     من المربعات؟ عامل كمنتج للمقارنات.
     من المكعبات؟ استخدم الفرق بين نمط المكعبات.
     إذا كانت ثلاثية الحدود:
     هل هي من الشكل$x^2+bx+c$؟ التراجع عن الفويل.
     هل هو من النموذج$ax^2+bx+c$؟
     إذا كانت a و c عبارة عن مربعات، فتحقق مما إذا كانت تناسب نمط المربع الثلاثي.
     استخدم طريقة التجربة والخطأ أو «$ac$».
     إذا كان يحتوي على أكثر من ثلاثة مصطلحات:
     استخدم طريقة التجميع.
  3. تحقق.
     هل يتم أخذها في الاعتبار بالكامل؟
     هل تتضاعف العوامل مرة أخرى في كثير الحدود الأصلي؟