6.4: منتجات خاصة بالمصنع
- Page ID
- 201555
في نهاية هذا القسم، ستكون قادرًا على:
- قوالب ثلاثية مربعة مثالية
- فروق عوامل المربعات
- مجاميع العوامل واختلافات المكعبات
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- قم بالتبسيط:\((3x^2)^3\).
- اضرب:\((m+4)^2\).
- اضرب:\((x−3)(x+3)\).
لقد رأينا أن بعض المقادير ذات الحدين والثلاثية تنتج عن منتجات خاصة - تربيع الحدين ومضاعفة المترافقات. إذا تعلمت التعرف على هذه الأنواع من كثيرات الحدود، يمكنك استخدام أنماط المنتجات الخاصة لتحليلها بسرعة أكبر.
قصص ثلاثية مربعة من فاكتور بيرفكت
بعض التثليث عبارة عن مربعات مثالية. وهي تنتج عن ضرب حاصل ضرب ذات حدين في حد ذاته. قمنا بتربيع معادلة ذات حدين باستخدام نمط المربعات ذات الحدين في الفصل السابق.
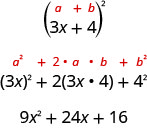
\(9x^2+24x+16\)يُطلق على المثلث اسم المربع الثلاثي المثالي. إنه مربع المعادلة ذات الحدين\(3x+4\).
في هذا الفصل، سوف تبدأ بثلاثية مربعة مثالية وتضعها في الاعتبار العوامل الرئيسية. يمكنك حساب هذا الثلاثي باستخدام الطرق الموضحة في القسم الأخير، نظرًا لأنه من النموذج\(ax^2+bx+c\). ولكن إذا أدركت أن الحدين الأول والأخير عبارة عن مربعات وأن الثلاثية تناسب نمط التثليث المربع المثالي، فستوفر على نفسك الكثير من العمل. هذا هو النمط - عكس نمط المربعات ذات الحدين.
إذا كانت\(a\)\(b\) الأرقام حقيقية
\[a^2+2ab+b^2=(a+b)^2\nonumber\]
\[a^2−2ab+b^2=(a−b)^2\nonumber\]
للاستفادة من هذا النمط، عليك أن تدرك أن ثلاثية معينة تناسبه. تحقق أولاً لمعرفة ما إذا كان المعامل الرئيسي مربعًا مثاليًا أم لا\(a^2\). تحقق بعد ذلك من أن المصطلح الأخير هو مربع مثالي,\(b^2\). ثم تحقق من المدى المتوسط - هل هو المنتج،\(2ab\)؟ إذا تم التحقق من كل شيء، يمكنك بسهولة كتابة العوامل.
عامل:\(9x^2+12x+4\).
- إجابة
-



عامل:\(4x^2+12x+9\).
- إجابة
-
\((2x+3)^2\)
عامل:\(9y^2+24y+16\).
- إجابة
-
\((3y+4)^2\)
تحدد علامة المدى المتوسط النمط الذي سنستخدمه. عندما يكون المدى المتوسط سلبيًا، فإننا نستخدم النمط\(a^2−2ab+b^2\) الذي يؤثر على ذلك\((a−b)^2\).
يتم تلخيص الخطوات هنا.
\(\begin{array} {lllll} \textbf{Step 1.} &\text{Does the trinomial fit the pattern?} &\quad &\hspace{7mm} a^2+2ab+b^2 &\hspace{7mm} a^2−2ab+b^2 \\ &\text{Are the first and last terms perfect squares?} &\quad & &\\ &\text{Write them as squares.} &\quad &\hspace{5mm}(a)^2\hspace{16mm} (b)^2 &\hspace{6mm}(a)^2\hspace{16mm} (b)^2 \\ &\text{Check the middle term. Is it }2ab? &\quad &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} \\ \textbf{Step 2.} &\text{Write the square of the binomial.} &\quad &\hspace{13mm} (a+b)^2 &\hspace{13mm} (a−b)^2 \\ \textbf{Step 3.} &\text{Check by multiplying.} & & & \end{array}\)
سنعمل الآن على واحدة حيث يكون المدى المتوسط سلبيًا.
عامل:\(81y^2−72y+16\).
- إجابة
-
المصطلحان الأول والأخير هما مربعات. تحقق مما إذا كان الحد الأوسط يناسب نمط المربع الثلاثي المثالي. الحد الأوسط سالب، لذلك سيكون المربع ذو الحدين\((a−b)^2\).
\(81 y^{2}-72 y+16\) هل المصطلحان الأول والأخير مربعات مثالية؟ 
تحقق من المدى المتوسط. 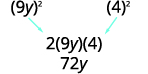
هل تتطابق\((a−b)^2\)؟ نعم. 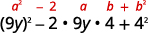
اكتب كمربع للرقم ذي الحدين. \((9 y-4)^{2}\) تحقق عن طريق الضرب:
\[(9y−4)^2\nonumber\]\[(9y)^2−2·9y·4+4^2\nonumber\]\[81y^2−72y+16\checkmark\nonumber\]
عامل:\(64y^2−80y+25\).
- إجابة
-
\((8y−5)^2\)
عامل:\(16z^2−72z+81\).
- إجابة
-
\((4z−9)^2\)
سيكون المثال التالي عبارة عن مثلث مربع مثالي مع متغيرين.
عامل:\(36x^2+84xy+49y^2\).
- إجابة
-
\(36 x^{2}+84 x y+49 y^{2}\) اختبر كل مصطلح للتحقق من النمط. 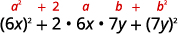
عامل. \((6 x+7 y)^{2}\) تحقق عن طريق الضرب.
\[(6x+7y)^2\nonumber\]\[(6x)^2+2·6x·7y+(7y)^2\nonumber\]\[36x^2+84xy+49y^2\checkmark\nonumber\]
عامل:\(49x^2+84xy+36y^2\).
- إجابة
-
\((7x+6y)^2\)
عامل:\(64m^2+112mn+49n^2\).
- إجابة
-
\((8m+7n)^2\)
تذكر أن الخطوة الأولى في التخصيم هي البحث عن أكبر عامل مشترك. قد تحتوي الأشكال الثلاثية المربعة المثالية على GCF في جميع المصطلحات الثلاثة ويجب أخذها في الاعتبار أولاً. وفي بعض الأحيان، بمجرد أخذ GCF في الاعتبار، ستتعرف على المربع الثلاثي المثالي.
عامل:\(100x^2y−80xy+16y\).
- إجابة
-
\(100 x^{2} y-80 x y+16 y\) هل هناك GCF؟ نعم\(4y\)، لذا ضع في اعتبارك ذلك. \(4 y\left(25 x^{2}-20 x+4\right)\) هل هذه ثلاثية مربعة مثالية؟ تحقق من النمط. 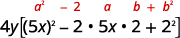
عامل. \(4 y(5 x-2)^{2}\) تذكر: احتفظ بعامل 4 y في المنتج النهائي. تحقق من:
\[4y(5x−2)^2\nonumber\]\[4y[(5x)2−2·5x·2+22]\nonumber\]\[4y(25x2−20x+4)\nonumber\]100x2y−80xy+16y\ علامة الاختيار\]
عامل:\(8x^2y−24xy+18y\).
- إجابة
-
\(2y(2x−3)^2\)
عامل:\(27p^2q+90pq+75q\).
- إجابة
-
\(3q(3p+5)^2\)
فروق عوامل المربعات
كان المنتج الخاص الآخر الذي رأيته في الفصل السابق هو نمط منتج الاقتران. لقد استخدمت هذا لضرب اثنين من الحدين المترافقين. في ما يلي مثال:
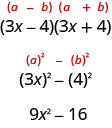
اختلاف عوامل المربعات لمنتج المترافقات.
إذا كانت\(a\)\(b\) الأرقام حقيقية،
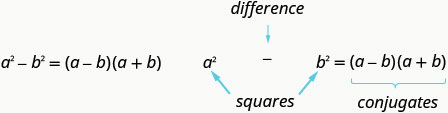
تذكر أن «الفرق» يشير إلى الطرح. لذلك، لاستخدام هذا النمط، يجب عليك التأكد من وجود حدين يتم فيه طرح مربعين.
عامل:\(64y^2−1\).
- إجابة
-




عامل:\(121m^2−1\).
- إجابة
-
\((11m−1)(11m+1)\)
عامل:\(81y^2−1\).
- إجابة
-
\((9y−1)(9y+1)\)
\(\begin{array} {llll} \textbf{Step 1.} &\text{Does the binomial fit the pattern?} &\qquad &\hspace{5mm} a^2−b^2 \\ &\text{Is this a difference?} &\qquad &\hspace{2mm} \text{____−____} \\ &\text{Are the first and last terms perfect squares?} & & \\ \textbf{Step 2.} &\text{Write them as squares.} &\qquad &\hspace{3mm} (a)^2−(b)^2 \\ \textbf{Step 3.} &\text{Write the product of conjugates.} &\qquad &(a−b)(a+b) \\ \textbf{Step 4.} &\text{Check by multiplying.} & & \end{array}\)
من المهم أن تتذكر أن مجاميع المربعات لا تدخل في ناتج المعادلات ذات الحدين. لا توجد عوامل ذات حدين تتضاعف معًا للحصول على مجموع المربعات. بعد إزالة أي GCF،\(a^2+b^2\) يكون التعبير أوليًا!
يوضح المثال التالي المتغيرات في كلا المصطلحين.
عامل:\(144x^2−49y^2\).
- إجابة
-
\(\begin{array} {lll} &\quad &144x^2−49y^2 \\ \text{Is this a difference of squares? Yes.} &\quad &(12x)^2−(7y)^2 \\ \text{Factor as the product of conjugates.} &\quad &(12x−7y)(12x+7y) \\ \text{Check by multiplying.} &\quad &(12x−7y)(12x+7y) \\ \text{Check by multiplying.} &\quad & \\ &\quad & \\ &\quad & \\ \hspace{14mm} (12x−7y)(12x+7y) &\quad & \\ \hspace{21mm} 144x^2−49y^2\checkmark &\quad & \end{array}\)
عامل:\(196m^2−25n^2\).
- إجابة
-
\((14m−5n)(14m+5n)\)
عامل:\(121p^2−9q^2\).
- إجابة
-
\((11p−3q)(11p+3q)\)
كما هو الحال دائمًا، يجب أن تبحث عن عامل مشترك أولاً عندما يكون لديك تعبير أو عامل. في بعض الأحيان قد «يخفي» عامل مشترك فرق المربعات ولن تتعرف على المربعات المثالية حتى تقوم بحساب GCF.
أيضًا، لتحليل المعادلة ذات الحدين بالكامل في المثال التالي، سنقوم بحساب فرق المربعات مرتين!
عامل:\(48x^4y^2−243y^2\).
- إجابة
-
\(\begin{array} {ll} &48x^4y^2−243y^2 \\ \text{Is there a GCF? Yes, }3y^2\text{—factor it out!} &3y^2(16x^4−81) \\ \text{Is the binomial a difference of squares? Yes.} &3y^2\left((4x^2)^2−(9)^2\right) \\ \text{Factor as a product of conjugates.} &3y^2(4x^2−9)(4x^2+9) \\ \text{Notice the first binomial is also a difference of squares!} &3y^2((2x)^2−(3)^2)(4x^2+9) \\ \text{Factor it as the product of conjugates.} &3y^2(2x−3)(2x+3)(4x^2+9) \end{array}\)
لا يمكن حساب العامل الأخير، وهو مجموع المربعات.
\(\begin{array} {l} \text{Check by multiplying:} \\ \hspace{10mm} 3y^2(2x−3)(2x+3)(4x^2+9) \\ \\ \\ \hspace{15mm} 3y^2(4x^2−9)(4x^2+9) \\ \hspace{20mm} 3y^2(16x^4−81) \\ \hspace{19mm} 48x^4y^2−243y^2\checkmark\end{array}\)
عامل:\(2x^4y^2−32y^2\).
- إجابة
-
\(2y^2(x−2)(x+2)(x^2+4)\)
عامل:\(7a^4c^2−7b^4c^2\).
- إجابة
-
\(7c^2(a−b)(a+b)(a^2+b^2)\)
يحتوي المثال التالي على كثير الحدود بـ 4 مصطلحات. حتى الآن، عندما حدث ذلك، قمنا بتجميع المصطلحات في قسمين وتم أخذها في الاعتبار من هناك. سنلاحظ هنا أن المصطلحات الثلاثة الأولى تشكل مربعًا ثلاثيًا مثاليًا.
عامل:\(x^2−6x+9−y^2\).
- إجابة
-
لاحظ أن المصطلحات الثلاثة الأولى تشكل مربعًا ثلاثيًا مثاليًا.
\(x^{2}-6 x+9-y^{2}\) عامل من خلال تجميع المصطلحات الثلاثة الأولى. \(\underbrace{x^{2}-6 x+9} - y^{2}\) استخدم النمط الثلاثي المربع المثالي. \((x-3)^{2}-y^{2}\) هل هذا فرق بين المربعات؟ نعم. نعم - اكتبها كمربعات. 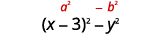
عامل كمنتج للمقارنات. 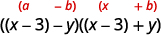
\((x-3-y)(x-3+y)\) قد ترغب في إعادة كتابة الحل كـ\((x−y−3)(x+y−3)\).
عامل:\(x^2−10x+25−y^2\).
- إجابة
-
\((x−5−y)(x−5+y)\)
عامل:\(x^2+6x+9−4y^2\).
- إجابة
-
\((x+3−2y)(x+3+2y)\)
مجاميع عوامل المكعبات والاختلافات بينها
هناك نمط خاص آخر للخصم، وهو النمط الذي لم نستخدمه عند ضرب كثيرات الحدود. هذا هو النمط لمجموع المكعبات والفرق بينها. سنكتب هذه الصيغ أولاً ثم نتحقق منها بالضرب.
\[a^3+b^3=(a+b)(a^2−ab+b^2\nonumber\]
\[a^3−b^3=(a−b)(a^2+ab+b^2)\nonumber\]
سوف نتحقق من النمط الأول ونترك الثاني لك.
| \(\color{red}(a+b) \color{black} \left(a^{2}-a b+b^{2}\right)\) | |
| قم بالتوزيع. | \(\color{red}a \color{black}\left(a^{2}-a b+b^{2}\right)+ \color{red}b \color{black}\left(a^{2}-a b+b^{2}\right)\) |
| اضرب. | \(a^{3}-a^{2} b+a b^{2}+a^{2} b-a b^{2}+b^{3}\) |
| اجمع بين المصطلحات المتشابهة. | \(a^{3}+b^{3}\) |
\[a^3+b^3=(a+b)(a^2−ab+b^2\nonumber\]\[a^3−b^3=(a−b)(a^2+ab+b^2)\nonumber\]
يبدو النمطان متشابهين جدًا، أليس كذلك؟ لكن لاحظ العلامات في العوامل. تتطابق علامة العامل ذي الحدين مع العلامة الموجودة في المعادلة الأصلية ذات الحدين. وعلامة الحد الأوسط للعامل الثلاثي هي عكس العلامة في المعادلة الأصلية ذات الحدين. إذا تعرفت على نمط العلامات، فقد يساعدك ذلك على حفظ الأنماط.

لا يمكن حساب العامل الثلاثي في مجموع وفرق نمط المكعبات.
سيكون من المفيد جدًا أن تتعلم التعرف على مكعبات الأعداد الصحيحة من 1 إلى 10، تمامًا كما تعلمت التعرف على المربعات. لقد قمنا بإدراج مكعبات الأعداد الصحيحة من 1 إلى 10 في الجدول.
| ن | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(n^3\) | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 |
عامل:\(x^3+64\).
- إجابة
-





عامل:\(x^3+27\).
- إجابة
-
\((x+3)(x^2−3x+9)\)
عامل:\(y^3+8\).
- إجابة
-
\((y+2)(y^2−2y+4)\)
- هل يتناسب الحد ذي الحدين مع مجموع أو فرق نمط المكعبات؟
هل هو مبلغ أم فرق؟
هل المصطلحات الأولى والأخيرة مكعبات مثالية؟ - اكتبها على هيئة مكعبات.
- استخدم إما مجموع أو فرق نمط المكعبات.
- قم بالتبسيط داخل الأقواس.
- تحقق من ذلك بضرب العوامل.
عامل:\(27u^3−125v^3\).
- إجابة
-
\(27 u^{3}-125 v^{3}\) هذا الحد ذو الحدين هو الفرق. المصطلحان الأول والأخير
عبارة عن مكعبات مثالية.اكتب المصطلحات في صورة مكعبات. 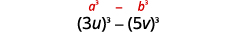
استخدم الفرق بين نمط المكعبات. 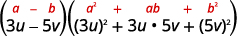
قم بالتبسيط. 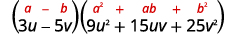
تحقق عن طريق الضرب. سنترك الشيك لك.
عامل:\(8x^3−27y^3\).
- إجابة
-
\((2x−3y)(4x^2+6xy+9y^2)\)
عامل:\(1000m^3−125n^3\).
- إجابة
-
\((10m−5n)(100m^2+50mn+25n^2)\)
في المثال التالي، نقوم أولاً بتحليل GCF. ثم يمكننا التعرف على مجموع المكعبات.
عامل:\(6x^3y+48y^4\).
- إجابة
-
\(6 x^{3} y+48 y^{4}\) عامل العامل المشترك. \(6 y\left(x^{3}+8 y^{3}\right)\) هذه المعادلة ذات الحدين عبارة عن مجموع. الحدان الأول والأخير
عبارة عن مكعبات مثالية.اكتب المصطلحات في صورة مكعبات. 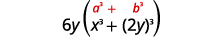
استخدم نمط مجموع المكعبات. 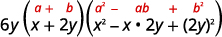
قم بالتبسيط. 
تحقق من:
وللتحقق من ذلك، قد تجد أنه من الأسهل ضرب مجموع عوامل المكعبات أولاً، ثم ضرب هذا المنتج في 6y.6y. سنترك عملية الضرب لك.
عامل:\(500p^3+4q^3\).
- إجابة
-
\(4(5p+q)(25p^2−5pq+q^2)\)
عامل:\(432c^3+686d^3\).
- إجابة
-
\(2(6c+7d)(36c^2−42cd+49d^2)\)
المصطلح الأول في المثال التالي هو مكعب ذو حدين.
عامل:\((x+5)^3−64x^3\).
- إجابة
-
\((x+5)^{3}-64 x^{3}\) هذا الحد ذو الحدين هو الفرق. المصطلحان الأول
والأخير عبارة عن مكعبات مثالية.اكتب المصطلحات في صورة مكعبات. 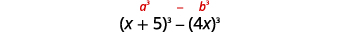
استخدم الفرق بين نمط المكعبات. 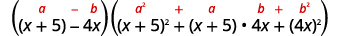
قم بالتبسيط. \((x+5-4 x)\left(x^{2}+10 x+25+4 x^{2}+20 x+16 x^{2}\right)\) \((-3 x+5)\left(21 x^{2}+30 x+25\right)\) تحقق عن طريق الضرب. سنترك الشيك لك.
عامل:\((y+1)^3−27y^3\).
- إجابة
-
\((−2y+1)(13y^2+5y+1)\)
عامل:\((n+3)^3−125n^3\).
- إجابة
-
\((−4n+3)(31n^2+21n+9)\)
يمكنك الوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات وممارسة إضافية مع تصميم المنتجات الخاصة.
المفاهيم الرئيسية
- نمط ثلاثي الحدود المربع المثالي: إذا كان a و b أرقامًا حقيقية،
\[\begin{array} {l} a^2+2ab+b^2=(a+b)^2 \\ a^2−2ab+b^2=(a−b)^2\end{array} \nonumber\]
- كيفية حساب التثليث المربع المثالي.
\(\begin{array} {lllll} \textbf{Step 1.} &\text{Does the trinomial fit the pattern?} &\quad &\hspace{7mm} a^2+2ab+b^2 &\hspace{7mm} a^2−2ab+b^2 \\ &\text{Are the first and last terms perfect squares?} &\quad & &\\ &\text{Write them as squares.} &\quad &\hspace{5mm}(a)^2\hspace{16mm} (b)^2 &\hspace{6mm}(a)^2\hspace{16mm} (b)^2 \\ &\text{Check the middle term. Is it }2ab? &\quad &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} \\ \textbf{Step 2.} &\text{Write the square of the binomial.} &\quad &\hspace{13mm} (a+b)^2 &\hspace{13mm} (a−b)^2 \\ \textbf{Step 3.} &\text{Check by multiplying.} & & & \end{array}\) - فرق نمط المربعات: إذا كانت a و ba و b عبارة عن أرقام حقيقية،
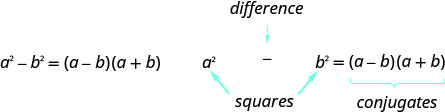
- كيفية حساب الاختلافات في المربعات.
\(\begin{array} {llll} \textbf{Step 1.} &\text{Does the binomial fit the pattern?} &\qquad &\hspace{5mm} a^2−b^2 \\ &\text{Is this a difference?} &\qquad &\hspace{2mm} \text{____−____} \\ &\text{Are the first and last terms perfect squares?} & & \\ \textbf{Step 2.} &\text{Write them as squares.} &\qquad &\hspace{3mm} (a)^2−(b)^2 \\ \textbf{Step 3.} &\text{Write the product of conjugates.} &\qquad &(a−b)(a+b) \\ \textbf{Step 4.} &\text{Check by multiplying.} & & \end{array}\) - نموذج مجموع المكعبات والفرق بينها
\(\begin{array} {l} a^3+b3=(a+b)(a^2−ab+b^2) \\ a^3−b^3=(a−b)(a^2+ab+b^2) \end{array} \) - كيفية حساب مجموع المكعبات أو الفرق بينها.
- هل يتناسب الحد ذي الحدين مع مجموع أو فرق نمط المكعبات؟
هل هو مبلغ أم فرق؟
هل المصطلحات الأولى والأخيرة مكعبات مثالية؟ - اكتبها على هيئة مكعبات.
- استخدم إما مجموع أو فرق نمط المكعبات.
- قم بالتبسيط داخل الأقواس
- تحقق من ذلك بضرب العوامل.
- هل يتناسب الحد ذي الحدين مع مجموع أو فرق نمط المكعبات؟


