6.2: العامل المشترك الأكبر والعامل حسب التجميع
- Page ID
- 201545
في نهاية هذا القسم، ستكون قادرًا على:
- أوجد العامل المشترك الأكبر لتعبيرين أو أكثر
- عامل: العامل المشترك الأكبر من دالة كثيرة الحدود
- عامل حسب التجميع
أوجد العامل المشترك الأكبر لتعبيرين أو أكثر
في وقت سابق قمنا بمضاعفة العوامل معًا للحصول على منتج. الآن، سنقوم بعكس هذه العملية؛ سنبدأ بمنتج ثم نقسمه إلى عوامله. يُطلق على تقسيم المنتج إلى عوامل اسم التخصيم.
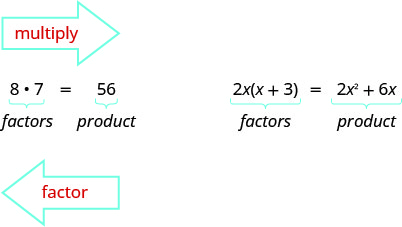
لقد تعلمنا كيفية حساب الأرقام للعثور على المضاعف المشترك الأصغر (LCM) لرقمين أو أكثر. سنقوم الآن بتحليل التعبيرات وإيجاد العامل المشترك الأكبر لتعبيرين أو أكثر. الطريقة التي نستخدمها مشابهة لما استخدمناه للعثور على LCM.
العامل المشترك الأكبر (GCF) لتعبيرين أو أكثر هو أكبر تعبير يمثل عاملًا لجميع التعبيرات.
نلخص الخطوات التي نستخدمها للعثور على العامل المشترك الأكبر.
- ضع كل معامل في الأعداد الأولية. اكتب جميع المتغيرات ذات الأسس في صورة موسعة.
- ضع قائمة بجميع العوامل - مطابقة العوامل الشائعة في عمود. في كل عمود، ضع دائرة حول العوامل المشتركة.
- قلل العوامل المشتركة التي تشترك فيها جميع التعبيرات.
- اضرب العوامل.
سيوضح لنا المثال التالي خطوات العثور على العامل المشترك الأكبر لثلاثة تعبيرات.
ابحث عن العامل المشترك الأكبر لـ\(21x^3,\space 9x^2,\space 15x\).
- إجابة
-
ضع كل معامل في الأعداد الأولية واكتب المتغيرات ذات الأسس في صورة موسعة. ضع دائرة حول العوامل المشتركة في كل عمود. قلل من العوامل المشتركة. 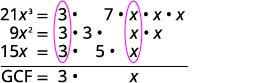
اضرب العوامل. GCF\(=3x\) GCF لـ\(21x^3\),\(9x^2\)\(15x\) وهو\(3x\).
ابحث عن العامل المشترك الأكبر:\(25m^4,\space 35m^3,\space 20m^2.\)
- إجابة
-
\(5m^2\)
ابحث عن العامل المشترك الأكبر:\(14x^3,\space 70x^2,\space 105x\).
- إجابة
-
\(7x\)
عامل العامل المشترك الأكبر من دالة كثيرة الحدود
من المفيد أحيانًا تمثيل رقم كمنتج لعوامل، على سبيل المثال، 12 كـ\(2·6\) أو\(3·4\). في الجبر، قد يكون من المفيد أيضًا تمثيل متعدد الحدود في شكل عامل. سنبدأ بمنتج، مثل\(3x^2+15x\)، وننتهي بعوامله،\(3x(x+5)\). للقيام بذلك، نطبق خاصية التوزيع «في الاتجاه المعاكس».
نذكر خاصية التوزيع هنا تمامًا كما رأيتها في الفصول السابقة و «بالعكس».
إذا كانت a و b و c أرقامًا حقيقية، إذن
\[a(b+c)=ab+ac \quad \text{and} \quad ab+ac=a(b+c)\nonumber\]
يتم استخدام النموذج الموجود على اليسار للتكاثر. يتم استخدام النموذج الموجود على اليمين كعامل.
إذن كيف تستخدم خاصية التوزيع لحساب كثير الحدود؟ ما عليك سوى العثور على GCF لجميع المصطلحات وكتابة متعدد الحدود كمنتج!
عامل:\(8m^3−12m^2n+20mn^2\).
- إجابة
-




عامل:\(9xy^2+6x^2y^2+21y^3\).
- إجابة
-
\(3y^2(3x+2x^2+7y)\)
عامل:\(3p^3−6p^2q+9pq^3\).
- إجابة
-
\(3p(p^2−2pq+3q^3)\)
- ابحث عن GCF لجميع مصطلحات كثيرة الحدود.
- أعد كتابة كل مصطلح كمنتج باستخدام GCF.
- استخدم خاصية التوزيع «العكسية» لتحليل التعبير.
- تحقق من ذلك بضرب العوامل.
نحن نستخدم «العامل» كاسم وفعل:
\[\begin{array} {ll} \text{Noun:} &\hspace{50mm} 7 \text{ is a factor of }14 \\ \text{Verb:} &\hspace{50mm} \text{factor }3 \text{ from }3a+3\end{array}\nonumber\]
عامل:\(5x^3−25x^2\).
- إجابة
-
ابحث عن GCF لـ\(5x^3\) و\(25x^2\). 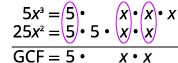
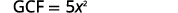
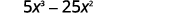
أعد كتابة كل مصطلح. 
عامل عامل GCF. 
تحقق من:
\[5x^2(x−5) \nonumber\]\[5x^2·x−5x^2·5 \nonumber\]
\[5x^3−25x^2 \checkmark\nonumber\]
عامل:\(2x^3+12x^2\).
- إجابة
-
\(2x^2(x+6)\)
عامل:\(6y^3−15y^2\).
- إجابة
-
\(3y^2(2y−5)\)
عامل:\(8x^3y−10x^2y^2+12xy^3\).
- إجابة
-
GCF الخاص بـ\(8x^3y,\space −10x^2y^2,\) and\(12xy^3\)
هو\(2xy\).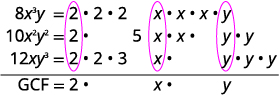

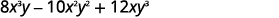
أعد كتابة كل مصطلح باستخدام GCF،\(2xy\). 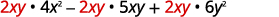
عامل عامل GCF. 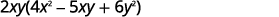
تحقق من:
\[2xy(4x^2−5xy+6y^2)\nonumber\]\[2xy·4x^2−2xy·5xy+2xy·6y^2\nonumber\]
\[8x^3y−10x^2y^2+12xy^3\checkmark\nonumber\]
عامل:\(15x^3y−3x^2y^2+6xy^3\).
- إجابة
-
\(3xy(5x^2−xy+2y^2)\)
عامل:\(8a^3b+2a^2b^2−6ab^3\).
- إجابة
-
\(2ab(4a^2+ab−3b^2)\)
عندما يكون المعامل الرئيسي سالبًا، نقوم بحساب السالب كجزء من GCF.
عامل:\(−4a^3+36a^2−8a\).
- إجابة
-
المعامل الرئيسي سلبي، وبالتالي فإن GCF سيكون سالبًا.
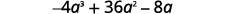
أعد كتابة كل مصطلح باستخدام GCF،\(−4a\). 
عامل عامل GCF. 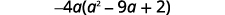
تحقق من:
\[−4a(a^2−9a+2)\nonumber\]\[−4a·a^2−(−4a)·9a+(−4a)·2\nonumber\]
\[−4a^3+36a^2−8a\checkmark\nonumber\]
عامل:\(−4b^3+16b^2−8b\).
- إجابة
-
\(−4b(b^2−4b+2)\)
عامل:\(−7a^3+21a^2−14a\).
- إجابة
-
\(−7a(a^2−3a+2)\)
حتى الآن كانت أكبر العوامل المشتركة لدينا هي الأحادية. في المثال التالي، العامل المشترك الأكبر هو المعادلة ذات الحدين.
عامل:\(3y(y+7)−4(y+7)\).
- إجابة
-
إن GCF هو الحد ذي الحدين\(y+7\).
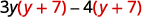
عامل GCF,\((y+7)\). \((y+7)(3 y-4)\) تحقق بنفسك عن طريق الضرب.
عامل:\(4m(m+3)−7(m+3)\).
- إجابة
-
\((m+3)(4m−7)\)
عامل:\(8n(n−4)+5(n−4)\).
- إجابة
-
\((n−4)(8n+5)\)
عامل حسب التجميع
في بعض الأحيان لا يوجد عامل مشترك لجميع مصطلحات كثيرة الحدود. عندما تكون هناك أربعة مصطلحات، نقوم بفصل متعدد الحدود إلى جزأين بحدين في كل جزء. ثم ابحث عن GCF في كل جزء. إذا كان من الممكن أخذ كثير الحدود في الاعتبار، ستجد عاملاً مشتركًا يظهر من كلا الجزأين. لا يمكن أخذ جميع كثيرات الحدود في الاعتبار. تمامًا مثل بعض الأرقام الأولية، تعتبر بعض كثيرات الحدود أولية.
عامل حسب التجميع:\(xy+3y+2x+6\).
- إجابة
-




عامل حسب التجميع:\(xy+8y+3x+24\).
- إجابة
-
\((x+8)(y+3)\)
عامل حسب التجميع:\(ab+7b+8a+56\).
- إجابة
-
\((a+7)(b+8)\)
- مصطلحات المجموعة مع العوامل المشتركة.
- حدد العامل المشترك في كل مجموعة.
- ضع في اعتبارك العامل المشترك من التعبير.
- تحقق من ذلك بضرب العوامل.
عامل حسب التجميع: ⓐ\(x^2+3x−2x−6\) ⓑ\(6x^2−3x−4x+2\).
- إجابة
-
ⓐ
\(\begin{array} {ll} \text{There is no GCF in all four terms.} &x^2+3x−2x−6 \\ \text{Separate into two parts.} &x^2+3x\quad −2x−6 \\ \begin{array} {l} \text{Factor the GCF from both parts. Be careful} \\ \text{with the signs when factoring the GCF from} \\ \text{the last two terms.} \end{array} &x(x+3)−2(x+3) \\ \text{Factor out the common factor.} &(x+3)(x−2) \\ \text{Check on your own by multiplying.} & \end{array}\)
ⓑ
\(\begin{array} {ll} \text{There is no GCF in all four terms.} &6x^2−3x−4x+2 \\ \text{Separate into two parts.} &6x^2−3x\quad −4x+2\\ \text{Factor the GCF from both parts.} &3x(2x−1)−2(2x−1) \\ \text{Factor out the common factor.} &(2x−1)(3x−2) \\ \text{Check on your own by multiplying.} & \end{array}\)
عامل حسب التجميع: ⓐ\(x^2+2x−5x−10\) ⓑ\(20x^2−16x−15x+12\).
- إجابة
-
ⓐ\((x−5)(x+2)\)
ⓑ\((5x−4)(4x−3)\)
عامل حسب التجميع: ⓐ\(y^2+4y−7y−28\) ⓑ\(42m^2−18m−35m+15\).
- إجابة
-
ⓐ\((y+4)(y−7)\)
ⓑ\((7m−3)(6m−5)\)
المفاهيم الرئيسية
- كيفية إيجاد العامل المشترك الأكبر (GCF) لتعبيرين.
- ضع كل معامل في الأعداد الأولية. اكتب جميع المتغيرات ذات الأسس في صورة موسعة.
- ضع قائمة بجميع العوامل - مطابقة العوامل الشائعة في عمود. في كل عمود، ضع دائرة حول العوامل المشتركة.
- قلل العوامل المشتركة التي تشترك فيها جميع التعبيرات.
- اضرب العوامل.
- خاصية التوزيع: إذا كانت\(a\)\(b\) ولا\(c\) تزال أرقامًا حقيقية، إذن
\[a(b+c)=ab+ac\quad \text{and}\quad ab+ac=a(b+c)\nonumber\]
يتم استخدام النموذج الموجود على اليسار للتكاثر. يتم استخدام النموذج الموجود على اليمين كعامل. - كيفية حساب العامل المشترك الأكبر من متعدد الحدود.
- ابحث عن GCF لجميع مصطلحات كثيرة الحدود.
- أعد كتابة كل مصطلح كمنتج باستخدام GCF.
- استخدم خاصية التوزيع «العكسية» لتحليل التعبير.
- تحقق من ذلك بضرب العوامل.
- عامل كاسم وفعل: نحن نستخدم «عامل» كاسم وفعل.
\[\begin{array} {ll} \text{Noun:} &\quad 7 \text{ is a factor of } 14\\ \text{Verb:} &\quad \text{factor }3 \text{ from }3a+3\end{array}\nonumber\]
- كيفية التعامل عن طريق التجميع.
- مصطلحات المجموعة مع العوامل المشتركة.
- حدد العامل المشترك في كل مجموعة.
- ضع في اعتبارك العامل المشترك من التعبير.
- تحقق من ذلك بضرب العوامل.
مسرد المصطلحات
- العوم
- يُطلق على تقسيم المنتج إلى عوامل اسم التخصيم.
- العامل المشترك الأكبر
- العامل المشترك الأكبر (GCF) لتعبيرين أو أكثر هو أكبر تعبير يمثل عاملًا لجميع التعبيرات.


