5.5: قسمة كثيرات الحدود
- Page ID
- 201502
في نهاية هذا القسم، ستكون قادرًا على:
- تقسيم الموحدين
- قسمة كثير الحدود على رقم أحادي
- قسمة كثيرات الحدود باستخدام القسمة المطولة
- قسمة كثيرات الحدود باستخدام القسمة التركيبية
- قسمة الدوال الكثيرة الحدود
- استخدم نظريات الباقي والعوامل
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
تقسيم الموحدين
نحن الآن على دراية بجميع خصائص الأسس واستخدمناها لضرب كثيرات الحدود. بعد ذلك، سنستخدم هذه الخصائص لتقسيم وحيدات الحدود وكثيرات الحدود.
ابحث عن حاصل القسمة:\(54a^2b^3÷ (−6ab^5)\).
الحل
عندما نقسم وحيدات الحد بأكثر من متغير واحد، نكتب كسرًا واحدًا لكل متغير.
\(\begin{array} {ll} {} &{54a^2b^3÷(−6ab^5)} \\[5pt] {\text{Rewrite as a fraction.}} &{\dfrac{54a^2b^3}{−6ab^5}} \\[5pt] {\text{Use fraction multiplication.}} &{\dfrac{54}{−6}·\dfrac{a^2}{a}·\dfrac{b^3}{b^5}} \\[5pt] {\text{Simplify and use the Quotient Property.}} &{−9·a·\dfrac{1}{b^2}} \\[5pt] {\text{Multiply.}} &{−\dfrac{9a}{b^2}} \end{array}\)
ابحث عن حاصل القسمة:\(−72a^7b^3÷(8a^{12}b^4)\).
- إجابة
-
\(−\dfrac{9}{a^5b}\)
ابحث عن حاصل القسمة:\(−63c^8d^3÷(7c^{12}d^2)\).
- إجابة
-
\(\dfrac{−9d}{c^4}\)
بمجرد التعرف على العملية وممارستها خطوة بخطوة عدة مرات، قد تتمكن من تبسيط جزء في خطوة واحدة.
ابحث عن حاصل القسمة:\(\dfrac{14x^7y^{12}}{21x^{11}y^6}\).
الحل
كن حذرًا جدًا في التبسيط\(\dfrac{14}{21}\) عن طريق تقسيم عامل مشترك، وتبسيط المتغيرات بطرح أسسها.
\(\begin{array} {ll} {} &{\dfrac{14x^7y^{12}}{21x^{11}y^6}} \\ {\text{Simplify and use the Quotient Property.}} &{\dfrac{2y^6}{3x^4}} \\ \end{array}\)
ابحث عن حاصل القسمة:\(\dfrac{28x^5y^{14}}{49x^9y^{12}}\).
- إجابة
-
\(\dfrac{4y^2}{7x^4}\)
ابحث عن حاصل القسمة:\(\dfrac{30m^5n^{11}}{48m^{10}n^{14}}\).
- إجابة
-
\(\dfrac{5}{8m^5n^3}\)
قسمة كثير الحدود على رقم أحادي الحد
الآن بعد أن عرفنا كيفية قسمة أحادية الحد على أحادية الحد، فإن الإجراء التالي هو قسمة كثير الحدود الذي يتكون من حدين أو أكثر على معادلة أحادية الحد. تعتمد الطريقة التي سنستخدمها لتقسيم كثير الحدود على صيغة أحادية الحد على خصائص إضافة الكسر. لذلك سنبدأ بمثال لمراجعة إضافة الكسور. يتم\(\dfrac{y}{5}+\dfrac{2}{5}\) تبسيط المبلغ إلى\(\dfrac{y+2}{5}\). الآن سنفعل ذلك في الاتجاه المعاكس لتقسيم كسر واحد إلى كسور منفصلة. على سبيل المثال،\(\dfrac{y+2}{5}\) يمكن كتابتها\(\dfrac{y}{5}+\dfrac{2}{5}\).
هذا هو «عكس» جمع الكسور وينص على أنه إذا كانت a و b و c عبارة عن أرقام فأين\(c\neq 0\)، إذن\(\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}\). سنستخدم هذا لتقسيم كثيرات الحدود على وحيدات الحد.
لتقسيم كثير الحدود على رقم أحادي، قسّم كل حد من كثير الحدود على الحد الأحادي.
ابحث عن حاصل القسمة:\((18x^3y−36xy^2)÷(−3xy)\).
الحل
\(\begin{array} {ll} {} &{(18x^3y−36xy^2)÷(−3xy)} \\[5pt] {\text{Rewrite as a fraction.}} &{\dfrac{18x^3y−36xy^2}{−3xy}} \\[5pt] {\text{Divide each term by the divisor. Be careful with the signs!}} &{\dfrac{18x^3y}{−3xy}−\dfrac{36xy^2}{−3xy}} \\[5pt] {\text{Simplify.}} &{−6x^2+12y} \end{array}\)
ابحث عن حاصل القسمة:\((32a^2b−16ab^2)÷(−8ab)\).
- إجابة
-
\(−4a+2b\)
ابحث عن حاصل القسمة:\((−48a^8b^4−36a^6b^5)÷(−6a^3b^3)\).
- إجابة
-
\(8a^5b+6a^3b^2\)
قسمة كثيرات الحدود باستخدام القسمة المطولة
قسمة كثير الحدود على ذات الحدين، نتبع إجراءً مشابهًا جدًا للقسمة الطويلة للأرقام. لذلك دعونا ننظر بعناية إلى الخطوات التي نتخذها عندما نقسم عددًا مكونًا من 3 أرقام، 875، على رقم مكون من رقمين، 25.
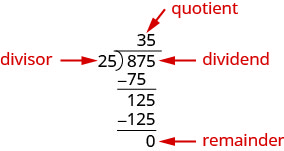
نتحقق من القسمة بضرب حاصل القسمة في المقسوم. إذا قمنا بالقسمة بشكل صحيح، يجب أن يساوي المنتج الأرباح.
\[\begin{array} {l} {35·25} \\ {875\checkmark} \\ \nonumber \end{array}\]
الآن سنقسم ثلاثية الحدود بمعادلة ذات حدين. أثناء قراءة المثال، لاحظ مدى تشابه الخطوات مع المثال العددي أعلاه.
ابحث عن حاصل القسمة:\((x^2+9x+20)÷(x+5)\).
الحل
| \(\require{enclose}\) | \(\qquad (x^2+9x+20) \div (x+5)\) |
| اكتبها كمشكلة قسمة طويلة. تأكد من أن الأرباح في شكلها القياسي. |
\(\qquad x+5\enclose{longdiv}{ x^2+9x+20\phantom{0}} \) |
|
اقسم\(x^2\) على\(x\). قد يكون من المفيد أن تسأل نفسك: «ما الذي أحتاج |
\(\qquad \begin{array}{r} {\color{red}x}\hspace{2.3em}\\[-3pt] {\color{red}x}+5\enclose{longdiv}{ {\color{red}x^2}+9x+20\phantom{0}} \end{array}\) |
| ضع الإجابة\(x\)، في حاصل القسمة على\(x\) المصطلح. اضرب\(x\) مرات\(x+5\). قم بترتيب الشروط المماثلة ضمن توزيعات الأرباح. |
\(\qquad \begin{array}{r}x\hspace{2.3em}\\[-3pt] x+5\enclose{longdiv}{x^2+9x+20\phantom{0}}\\[-3pt] \underline{\color{red}x^2+5x}\hspace{2.4em} \end{array}\) |
| اطرح\(x^2+5x\) من\(x^2+9x\). قد تجد أنه من الأسهل تغيير العلامات ثم إضافتها. ثم قم بإسقاط الفصل الدراسي الأخير،\(20.\) |
\(\qquad \begin{array}{r}x\hspace{2.3em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] {\color{red}4x+20}\hspace{0.5em} \end{array}\) |
اقسم\(4x\) على\(x\). قد يكون من المفيد أن تسأل نفسك: «ما الذي أحتاج إلى\(x\) مضاعفته للحصول عليه\(4x\)؟» ضع الإجابة\(4\)، في حاصل القسمة على الحد الثابت. |
\(\qquad \begin{array}{r}x+\phantom{0}{\color{red}4}\hspace{.5em}\\[-3pt] {\color{red}x}+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] {\color{red}4x}+20\hspace{0.5em} \end{array}\) |
| اضرب 4 مرات\(x+5\). |
\(\qquad \begin{array}{r}x+\phantom{0}4\hspace{.5em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] 4x+20\hspace{0.5em}\\[-3pt] \underline{ \color{red}4x+20}\hspace{.5em} \end{array}\) |
| اطرح\(4x+20\) من\(4x+20\). |
\(\qquad \begin{array}{r}x+\phantom{0}4\hspace{.5em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] 4x+20\hspace{.5em}\\[-3pt] \underline{{\color{red}-}4x+({\color{red}-}20)}\\[-3pt] 0\hspace{.33em}\end{array}\) |
|
تحقق من: \(\begin{array} {ll} {\text{Multiply the quotient by the divisor.}} &{(x+4)(x+5)} \\ {\text{You should get the dividend.}} &{x^2+9x+20\checkmark}\\ \end{array}\) |
ابحث عن حاصل القسمة:\((y^2+10y+21)÷(y+3)\).
- إجابة
-
\(y+7\)
ابحث عن حاصل القسمة:\((m^2+9m+20)÷(m+4)\).
- إجابة
-
\(m+5\)
عندما قسمنا 875 على 25، لم يكن لدينا أي متبقٍ. لكن في بعض الأحيان يؤدي تقسيم الأرقام إلى ترك الباقي. وينطبق الشيء نفسه عندما نقسم كثيرات الحدود. في المثال التالي، سيكون لدينا قسم يترك الباقي. نكتب الباقي في صورة كسر مع المقسوم باعتباره المقام.
انظر إلى الأرباح في الأمثلة السابقة. تمت كتابة المصطلحات بترتيب تنازلي للدرجات، ولم تكن هناك درجات مفقودة. سيكون العائد في هذا المثال\(x^4−x^2+5x−6\). إنه يفتقر إلى\(x^3\) مصطلح. سنضيف\(0x^3\) كعنصر نائب.
ابحث عن حاصل القسمة:\((x^4−x^2+5x−6)÷(x+2)\).
الحل
لاحظ أنه لا يوجد\(x^3\) مصطلح في توزيع الأرباح. سنضيف\(0x^3\) كعنصر نائب.
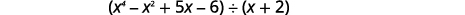 |
|
| اكتبها كمشكلة قسمة طويلة. تأكد من أن توزيع الأرباح في شكل قياسي مع عناصر نائبة للمصطلحات المفقودة. | 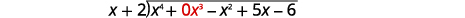 |
| اقسم\(x^4\) على\(x\). ضع الإجابة\(x^3\)، في حاصل القسمة على\(x^3\) المصطلح. اضرب\(x^3\) مرات\(x+2\). اصطف المصطلحات المشابهة. اطرح المصطلح التالي ثم اسقطه. |
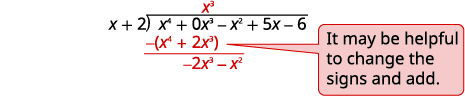 |
| اقسم\(−2x^3\) على\(x\). ضع الإجابة\(−2x^2\)، في حاصل القسمة على\(x^2\) المصطلح. اضرب\(−2x^2\) مرات\(x+1\). اصطف المصطلحات المتشابهة Subtract واسقط المصطلح التالي. |
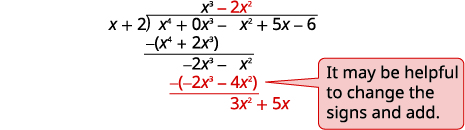 |
| اقسم\(3x^2\) على\(x\). ضع الإجابة\(3x\)، في حاصل القسمة على\(x\) المصطلح. اضرب\(3x\) مرات\(x+1\). اصطف المصطلحات المشابهة. اطرح المصطلح التالي واسقطه. |
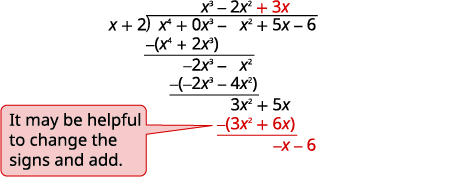 |
| اقسم\(−x\) على\(x\). ضع الإجابة\(−1\)، في حاصل القسمة على الحد الثابت. اضرب\(−1\) مرات\(x+1\). اصطف المصطلحات المشابهة. قم بتغيير العلامات، أضف. اكتب الباقي في صورة كسر باستخدام المقسوم باعتباره المقام. |
 |
| للتحقق، اضرب\((x+2)(x^3−2x^2+3x−1−4x+2)\). يجب أن تكون النتيجة\(x^4−x^2+5x−6\). |
ابحث عن حاصل القسمة:\((x^4−7x^2+7x+6)÷(x+3)\).
- إجابة
-
\(x^3−3x^2+2x+1+3x+3\)
ابحث عن حاصل القسمة:\((x^4−11x^2−7x−6)÷(x+3)\).
- إجابة
-
\(x^3−3x^2−2x−1−3x+3\)
في المثال التالي، سنقسم على\(2a−3\). عندما نقسم، سيتعين علينا النظر في الثوابت والمتغيرات.
ابحث عن حاصل القسمة:\((8a^3+27)÷(2a+3)\).
الحل
هذه المرة سنعرض التقسيم كله في خطوة واحدة. نحتاج إلى إضافة عنصرين نائبين من أجل التقسيم.
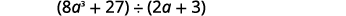 |
|
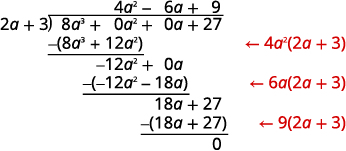 |
للتحقق، اضرب\((2a+3)(4a^2−6a+9)\).
يجب أن تكون النتيجة\(8a^3+27\).
ابحث عن حاصل القسمة:\((x^3−64)÷(x−4)\).
- إجابة
-
\(x^2+4x+16\)
ابحث عن حاصل القسمة:\((125x^3−8)÷(5x−2)\).
- إجابة
-
\(25x^2+10x+4\)
قسمة كثيرات الحدود باستخدام القسمة التركيبية
كما ذكرنا سابقًا، يحب علماء الرياضيات العثور على أنماط لتسهيل عملهم. نظرًا لأن القسمة الطويلة يمكن أن تكون مملة، فلننظر إلى التقسيم الطويل الذي قمنا به في المثال ونبحث عن بعض الأنماط. سنستخدم هذا كأساس لما يسمى التقسيم التركيبي. تظهر نفس المشكلة في تنسيق القسمة التركيبية بعد ذلك.
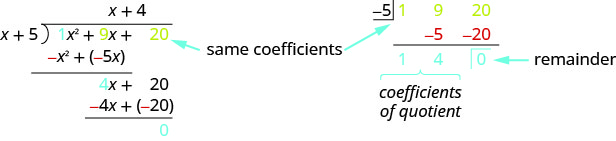
يؤدي التقسيم التركيبي بشكل أساسي إلى إزالة المتغيرات والأرقام المتكررة غير الضرورية. هنا\(x^2\) تتم إزالة جميع الأراضي. بالإضافة إلى\(−x^2\) الرمال\(−4x\) لأنها تتعارض مع المصطلح أعلاه.\(x\)
- الصف الأول من التقسيم التركيبي هو معاملات الأرباح. \(−5\)هذا هو عكس 5 في المقسوم.
- الصف الثاني من القسمة التركيبية هو الأرقام الموضحة باللون الأحمر في مشكلة القسمة.
- الصف الثالث من القسمة التركيبية هو الأرقام الموضحة باللون الأزرق في مشكلة القسمة.
لاحظ ظهور حاصل القسمة والباقي في الصف الثالث.
\[\text{Synthetic division only works when the divisor is of the form }x−c. \nonumber \]
سوف يشرح المثال التالي العملية.
استخدم القسمة التركيبية لإيجاد حاصل القسمة والباقي عند\(2x^3+3x^2+x+8\) القسمة على\(x+2\).
الحل
| اكتب الأرباح بصلاحيات متناقصة تبلغ\(x\). | 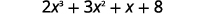 |
| اكتب معاملات المصطلحات في صورة الصف الأول من القسمة التركيبية. |
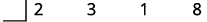 |
| اكتب اسم المقسوم\(x−c\) ثم ضع c في القسم التركيبي في مربع المقسوم. |
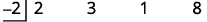 |
| انزل المعامل الأول إلى الصف الثالث. | 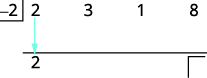 |
| اضرب هذا المعامل في المقسوم ثم ضع النتيجة في الصف الثاني تحت المعامل الثاني. |
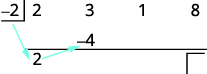 |
| أضف العمود الثاني، مع وضع النتيجة في الصف الثالث. | 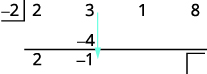 |
| اضرب هذه النتيجة في المقسوم ثم ضع النتيجة في الصف الثاني تحت المعامل الثالث. |
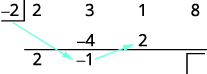 |
| أضف العمود الثالث، مع وضع النتيجة في الصف الثالث. | 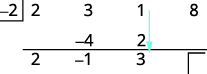 |
| اضرب هذه النتيجة في المقسوم ثم ضع النتيجة في الصف الثالث تحت المعامل الثالث. |
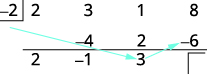 |
| أضف العمود الأخير، مع وضع النتيجة في الصف الثالث. | 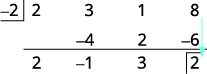 |
| حاصل القسمة هو\(2x^2−1x+3\) والباقي هو 2. |
تم الانتهاء من التقسيم. الأرقام في الصف الثالث تعطينا النتيجة. \(2\space\space\space−1\space\space\space3\)هذه هي معاملات حاصل القسمة. حاصل القسمة هو\(2x^2−1x+3\). الرقم 2 الموجود في المربع الموجود في الصف الثالث هو الباقي.
تحقق من:
\(\begin{align} (\text{quotient})(\text{divisor}) + \text{remainder} &= \text{dividend} \nonumber\\ (2x^2−1x+3)(x+2)+2 &\overset{?}{=} 2x^3+3x^2+x+8 \nonumber\\ 2x^3−x^2+3x+4x^2−2x+6+2 &\overset{?}{=} 2x^3+3x^2+x+8 \nonumber\\ 2x^3+3x^2+x+8 &= 2x^3+3x^2+x+8\checkmark \nonumber \end{align} \)
استخدم القسمة التركيبية لإيجاد حاصل القسمة والباقي عند\(3x^3+10x^2+6x−2\) القسمة على\(x+2\).
- إجابة
-
\(3x^2+4x−2;\space 2\)
استخدم القسمة التركيبية لإيجاد حاصل القسمة والباقي عند\(4x^3+5x^2−5x+3\) القسمة على\(x+2\).
- إجابة
-
\(4x^2−3x+1; 1\)
في المثال التالي، سنقوم بكل الخطوات معًا.
استخدم القسمة التركيبية لإيجاد حاصل القسمة والباقي عند\(x^4−16x^2+3x+12\) القسمة على\(x+4\).
الحل
مصطلح كثير الحدود\(x^4−16x^2+3x+12\) له ترتيب تنازلي ولكننا نلاحظ عدم وجود\(x^3\) مصطلح. سنضيف 0 كعنصر نائب\(x^3\) للمصطلح. في\(x−c\) الشكل، المقسوم هو\(x−(−4)\).
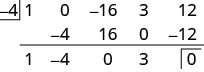
قمنا بتقسيم\(4^{\text{th}}\) درجة كثيرة الحدود على\(1^{\text{st}}\) درجة كثيرة الحدود بحيث يكون حاصل القسمة عبارة عن\(3^{\text{rd}}\) درجة متعددة الحدود.
عند القراءة من الصف الثالث، يحتوي حاصل القسمة على المعاملات\(1\space\space\space−4\space\space\space0\space\space\space3\)، وهي\(x^3−4x^2+3\). الباقي
هو 0.
استخدم القسمة التركيبية لإيجاد حاصل القسمة والباقي عند\(x^4−16x^2+5x+20\) القسمة على\(x+4\).
- إجابة
-
\(x^3−4x^2+5;\space 0\)
استخدم القسمة التركيبية لإيجاد حاصل القسمة والباقي عند\(x^4−9x^2+2x+6\) القسمة على\(x+3\).
- إجابة
-
\(x^3−3x^2+2;\space 0\)
قسمة الدوال الكثيرة الحدود
مثلما يمكن تقسيم كثيرات الحدود، يمكن أيضًا تقسيم الدوال متعددة الحدود.
للوظائف\(f(x)\) وأين\(g(x)\)\(g(x)\neq 0\)،
\[\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)} \nonumber\]
للوظائف\(f(x)=x^2−5x−14\) وابحث\(g(x)=x+2\) عن:
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−4)\).
الحل
ⓐ
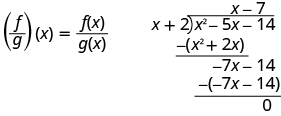
\(\begin{array} {ll} {\text{Substitute for }f(x)\text{ and }g(x).} &{\left(\dfrac{f}{g}\right)(x)=\dfrac{x^2−5x−14}{x+2}} \\[5pt] {\text{Divide the polynomials.}} &{\left(\dfrac{f}{g}\right)(x)=x−7} \end{array} \)
ⓑ جزئيًا ⓐ وجدنا\(\left(\dfrac{f}{g}\right)(x)\) والآن يُطلب منا العثور عليه\(\left(\dfrac{f}{g}\right)(−4)\).
\(\begin{array} {ll} {} &{\left(\dfrac{f}{g}\right)(x)=x−7} \\[5pt] {\text{To find }\left(\dfrac{f}{g}\right)(−4), \text{ substitute }x=−4.} &{\left(\dfrac{f}{g}\right)(−4)=−4−7} \\[5pt] {} &{\left(\dfrac{f}{g}\right)(−4)=−11} \end{array}\)
للوظائف\(f(x)=x^2−5x−24\) وابحث\(g(x)=x+3\) عن:
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−3)\).
- الإجابة أ
-
\(\left(\dfrac{f}{g}\right)(x)=x−8\)
- الإجابة ب
-
\(\left(\dfrac{f}{g}\right)(−3)=−11\)
للوظائف\(f(x)=x2−5x−36\) وابحث\(g(x)=x+4\) عن:
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−5)\).
- الإجابة أ
-
\(\left(\dfrac{f}{g}\right)(x)=x−9\)
- الإجابة ب
-
\(\left(\dfrac{f}{g}\right)(x)=x−9\)
استخدم نظرية الباقي والعامل
دعونا نلقي نظرة على مشاكل التقسيم التي عملنا عليها للتو والتي انتهت بالباقي. تم تلخيصها في الرسم البياني أدناه. إذا أخذنا الأرباح من كل مشكلة في القسمة واستخدمناها لتحديد دالة، نحصل على الوظائف الموضحة في المخطط. عند كتابة المقسوم كـ\(x−c\)، تكون قيمة الدالة عند\(c\)،\(f(c)\)، هي نفس القيمة المتبقية من مشكلة القسمة.
| الأرباح | المقسوم\(x−c\) | الباقي | وظيفة | \(f(c)\) |
|---|---|---|---|---|
| \(x^4−x^2+5x−6\) | \ (x−c\)» data-valign= «top">\(x−(−2)\) | \(−4\) | \(f(x)=x^4−x^2+5x−6\) | \ (f (c)\)» data-valign= top>\(−4\) |
| \(3x^3−2x^2−10x+8\) | \ (x−c\)» data-valign= «top">\(x−2\) | 4 | \(f(x)=3x^3−2x^2−10x+8\) | \ (f (c)\)» data-valign= «top">4 |
| \(x^4−16x^2+3x+15\) | \ (x−c\)» data-valign= «top">\(x−(−4)\) | 3 | \(f(x)=x^4−16x^2+3x+15\) | \ (f (c)\)» data-valign= «top">3 |
لرؤية هذا بشكل عام، ندرك أنه يمكننا التحقق من مشكلة القسمة بضرب حاصل القسمة في المقسوم وإضافة الباقي. في تدوين الدالة، يمكننا القول، للحصول على الأرباح\(f(x)\)، نضرب حاصل القسمة،\(q(x)\) مضروبًا في المقسوم\(x−c\)، ونضيف الباقي\(r\).
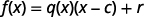 |
|
| إذا قمنا بتقييم هذا في\(c\)، نحصل على: | 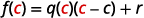 |
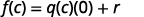 |
|
 |
هذا يقودنا إلى نظرية الباقي.
إذا كانت الدالة\(f(x)\) كثيرة الحدود مقسمة على\(x−c\)، فإن الباقي هو\(f(c)\).
استخدم نظرية الباقي لإيجاد الباقي عند\(f(x)=x^3+3x+19\) القسمة على\(x+2\).
الحل
لاستخدام نظرية الباقي، يجب أن نستخدم المقسوم في\(x−c\) الشكل. يمكننا كتابة المقسوم\(x+2\) كـ\(x−(−2)\). لذلك، لدينا\(c\)\(−2\).
للعثور على الباقي، نقوم بتقييم\(f(c)\) أيهما\(f(−2)\).
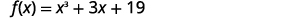 |
|
| للتقييم\(f(−2)\)، استبدل\(x=−2\). | 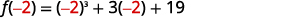 |
| قم بالتبسيط. | 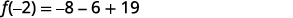 |
 |
|
| الباقي هو 5 عند\(f(x)=x^3+3x+19\) تقسيمه على\(x+2\). | |
| تحقق: استخدم التقسيم الاصطناعي للتحقق. |
|
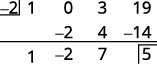 |
|
| الباقي هو 5. |
استخدم نظرية الباقي لإيجاد الباقي عند\(f(x)=x^3+4x+15\) القسمة على\(x+2\).
- إجابة
-
\(−1\)
استخدم نظرية الباقي لإيجاد الباقي عند\(f(x)=x^3−7x+12\) القسمة على\(x+3\).
- إجابة
-
\(6\)
عندما\(8a^3+27\) قسمنا\(2a+3\) على المثال كانت النتيجة\(4a^2−6a+9\). للتحقق من عملنا، نضرب\(2a+3\) للحصول\(4a2−6a+9\) عليه\(8a^3+27\).
\[(4a^2−6a+9)(2a+3)=8a^3+27 \nonumber \]
مكتوبة بهذه الطريقة، يمكننا أن نرى ذلك\(4a^2−6a+9\)\(2a+3\) وهي عوامل\(8a^3+27\). عندما قمنا بالقسمة، كان الباقي صفرًا.
عندما يقسم\(x−c\) المقسوم دالة كثيرة الحدود\(f(x)\) وينتج عنه باقي الصفر، نقول\(x−c\) إنه عامل\(f(x)\).
والعكس صحيح أيضًا. \(x−c\)إذا كان عاملًا،\(f(x)\)\(x−c\) فسيتم تقسيم الدالة كثيرة الحدود مما ينتج عنه باقي الصفر.
سنذكر هذا في نظرية العوامل.
لأي دالة متعددة الحدود\(f(x)\)،
- \(x−c\)إذا كان أحد عوامل\(f(x)\)، إذن\(f(c)=0\)
- إذا كان\(f(c)=0\)، إذن،\(x−c\) هو عامل\(f(x)\)
استخدم نظرية الباقي لتحديد\(x−4\) ما إذا كان أحد عوامل\(f(x)=x^3−64\).
الحل
تخبرنا نظرية العامل أن هذا\(x−4\) هو عامل\(f(x)=x^3−64\) IF\(f(4)=0\).
\(\begin{array} {ll} {} &{f(x)=x^3−64} \\[5pt] {\text{To evaluate }f(4) \text{ substitute } x=4.} &{f(4)=4^3−64} \\[5pt] {\text{Simplify.}} &{f(4)=64−64} \\[5pt]{\text{Subtract.}} &{f(4)=0} \end{array}\)
منذ ذلك الحين\(f(4)=0, x−4\) هو عامل\(f(x)=x^3−64\).
استخدم نظرية العامل لتحديد\(x−5\) ما إذا كان أحد عوامل\(f(x)=x^3−125\).
- إجابة
-
نعم
استخدم نظرية العامل لتحديد\(x−6\) ما إذا كان أحد عوامل\(f(x)=x^3−216\).
- إجابة
-
نعم
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية مع تقسيم كثيرات الحدود.
- قسمة كثير الحدود على معادلة ذات حدين
- نظرية القسمة التركيبية والباقي
المفاهيم الرئيسية
- قسمة كثير الحدود على مقياس أحادي الحد
- لتقسيم كثير الحدود على رقم أحادي، قسّم كل حد من كثير الحدود على الحد الأحادي.
- قسم الدوال الكثيرة الحدود
- للوظائف\(f(x)\) وأين\(g(x)\)\(g(x)\neq 0\)،
\(\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)}\)
- للوظائف\(f(x)\) وأين\(g(x)\)\(g(x)\neq 0\)،
- نظرية الباقي
- إذا كانت الدالة\(f(x)\) كثيرة الحدود مقسمة على\(x−c\)، فإن الباقي هو\(f(c)\).
- نظرية العوامل: لأي دالة كثيرة الحدود\(f(x)\)،
- \(x−c\)إذا كان أحد عوامل\(f(x)\)، إذن\(f(c)=0\)
- إذا كان\(f(c)=0\)، إذن،\(x−c\) هو عامل\(f(x)\)


