5.4: ضرب كثيرات الحدود
- Page ID
- 201481
في نهاية هذا القسم، ستكون قادرًا على:
- ضرب وحيدات الحد
- اضرب دالة كثيرة الحدود في معادلة أحادية
- ضرب معادلة ذات حدين في معادلة ذات حدين
- ضرب كثير الحدود في كثير الحدود
- ضاعف المنتجات الخاصة
- ضرب الدوال الكثيرة الحدود
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
ضرب وحيدات الحدود
نحن على استعداد لإجراء عمليات على كثيرات الحدود. نظرًا لأن وحيدات الحد هي تعبيرات جبرية، يمكننا استخدام خصائص الأسس لضرب وحيدات الحد.
اضرب:
- \((3x^2)(−4x^3)\)
- \(\left(\frac{5}{6}x^3y\right)(12xy^2).\)
- الإجابة أ
-
\(\begin{array} {ll} {} &{(3x^2)(−4x^3)} \\ {\text{Use the Commutative Property to rearrange the terms.}} &{3·(−4)·x^2·x^3} \\ {\text{}} &{−12x^5} \\ \end{array} \)
- الإجابة ب
-
\(\begin{array} {ll} {} &{\left(\frac{5}{6}x^3y\right)(12xy^2)} \\ {\text{Use the Commutative Property to rearrange the terms.}} &{\frac{5}{6}·12·x^3·x·y·y^2} \\ {\text{Multiply.}} &{10x^4y^3} \\ \end{array} \)
اضرب:
- \((5y^7)(−7y^4)\)
- \((25a^4b^3)(15ab^3)\)
- الإجابة أ
-
\(−35y^{11}\)
- الإجابة ب
-
\(375 a^5b^6\)
اضرب:
- \((−6b^4)(−9b^5)\)
- \((23r^5s)(12r^6s^7).\)
- الإجابة أ
-
\(54b^9\)
- الإجابة ب
-
\(276 r^{11}s^8\)
ضرب كثير الحدود في معادلة أحادية الحد
إن ضرب كثير الحدود في معادلة أحادية الحد هو في الواقع مجرد تطبيق خاصية التوزيع.
اضرب:
- \(−2y(4y^2+3y−5)\)
- \(3x^3y(x^2−8xy+y^2)\).
- الإجابة أ
-
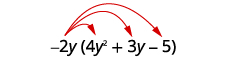
قم بالتوزيع. 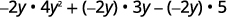
اضرب. 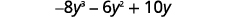
- الإجابة ب
-
\(\begin{array} {ll} {} &{3x^3y(x^2−8xy+y^2)} \\ {\text{Distribute.}} &{3x^3y⋅x^2+(3x^3y)⋅(−8xy)+(3x^3y)⋅y^2} \\ {\text{Multiply.}} &{3x^5y−24x^4y^2+3x^3y^3} \\ \end{array} \)
اضرب:
- \(-3y(5y^2+8y^{7})\)
- \(4x^2y^2(3x^2−5xy+3y^2)\)
- الإجابة أ
-
\(−15y^3−24y^8\)
- الإجابة ب
-
\(12x^4y^2−20x^3y^3+12x^2y^4\)
اضرب:
- \(4x^2(2x^2−3x+5)\)
- \(−6a^3b(3a^2−2ab+6b^2)\)
- الإجابة أ
-
\(8x^4−12x^3+20x^2\)
- الإجابة ب
-
\(−18a^5b+12a^4b^2−36a^3b^3\)
ضرب معادلة ذات حدين في معادلة ذات حدين
مثلما توجد طرق مختلفة لتمثيل ضرب الأرقام، هناك العديد من الطرق التي يمكن استخدامها لضرب معادلة ذات حدين في معادلة ذات حدين. سنبدأ باستخدام خاصية التوزيع.
اضرب:
- \((y+5)(y+8)\)
- \((4y+3)(2y−5)\).
- إجابة
-
ⓐ
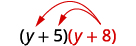
قم بالتوزيع\((y+8)\). 
وزّع مرة أخرى. 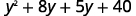
اجمع بين المصطلحات المتشابهة. 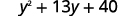
ⓑ
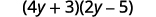
قم بالتوزيع. 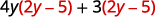
وزّع مرة أخرى. 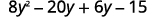
اجمع بين المصطلحات المتشابهة. 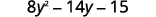
اضرب:
- \((x+8)(x+9)\)
- \((3c+4)(5c−2)\).
- الإجابة أ
-
\(x^2+17x+72\)
- الإجابة ب
-
\(15c^2+14c−8\)
اضرب:
- \((5x+9)(4x+3)\)
- \((5y+2)(6y−3)\).
- الإجابة أ
-
\(20x^2+51x+27\)
- الإجابة ب
-
\(30y^2−3y−6\)
إذا قمت بضرب الحدين في كثير من الأحيان بما فيه الكفاية، فقد تلاحظ النمط. لاحظ أن المصطلح الأول في النتيجة هو نتاج المصطلحات الأولى في كل معادلة ذات حدين. المصطلحان الثاني والثالث هما نتاج ضرب الحدين الخارجيين ثم الحدين الداخليين. وينتج المصطلح الأخير عن ضرب الحدين الأخيرين،
نحن نختصر «الأول، الخارجي، الداخلي، الأخير» باسم FOIL. تشير الحروف إلى «الأول، الخارجي، الداخلي، الأخير». نحن نستخدم هذا كطريقة أخرى لضرب المعادلات ذات الحدين. من السهل تذكر كلمة FOIL وتضمن العثور على جميع المنتجات الأربعة.
دعونا نضرب\((x+3)(x+7)\) باستخدام كلتا الطريقتين.

نلخص خطوات طريقة FOIL أدناه. تنطبق طريقة FOIL فقط على ضرب المقادير ذات الحدين، وليس على كثيرات الحدود الأخرى!

عندما تقوم بالضرب باستخدام طريقة FOIL، فإن رسم الخطوط سيساعد عقلك على التركيز على النمط وتسهيل تطبيقه.
الآن سنقوم بعمل مثال حيث نستخدم نمط FOIL لضرب اثنين من الحدين.
اضرب:
- \((y−7)(y+4)\)
- \((4x+3)(2x−5)\).
- إجابة
-
أ.

ب.

اضرب:
- \((x−7)(x+5)\)
- \((3x+7)(5x−2)\).
- إجابة
-
أ.\(x^2−2x−35\)
ب.\(15x^2+29x−14\)
اضرب:
- \((b−3)(b+6)\)
- \((4y+5)(4y−10)\).
- إجابة
-
أ.\(b^2+3b−18\)
ب.\(16y^2−20y−50\)
كانت المنتجات النهائية في المثال الأخير عبارة عن مصطلحات ثلاثية لأننا نستطيع الجمع بين المصطلحين المتوسطين. هذا ليس هو الحال دائمًا.
اضرب:
- \((n^2+4)(n−1)\)
- \((3pq+5)(6pq−11)\).
- إجابة
-
أ.
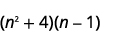
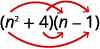
الخطوة 1. اضرب المصطلحات الأولى. 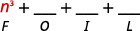
الخطوة 2. اضرب المصطلحات الخارجية. 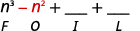
الخطوة 3. اضرب المصطلحات الداخلية. 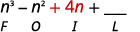
الخطوة 4. اضرب المصطلحات الأخيرة. 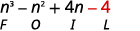
الخطوة 5. اجمع بين المصطلحات المتشابهة - لا يوجد شيء. 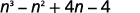
ب.
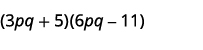
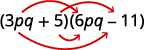
الخطوة 1. اضرب المصطلحات الأولى. 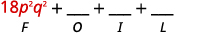
الخطوة 2. اضرب المصطلحات الخارجية. 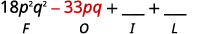
الخطوة 3. اضرب المصطلحات الداخلية. 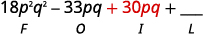
الخطوة 4. اضرب المصطلحات الأخيرة. 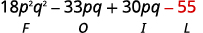
الخطوة 5. اجمع بين المصطلحات المتشابهة. 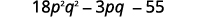
اضرب:
- \((x^2+6)(x−8)\)
- \((2ab+5)(4ab−4)\).
- إجابة
-
أ.\(x^3−8x^2+6x−48\)
ب.\(8a^2b^2+12ab−20\)
اضرب:
- \((y^2+7)(y−9)\)
- \((2xy+3)(4xy−5)\).
- إجابة
-
أ.\(y^3−9y^2+7y−63\)
ب.\(8x^2y^2+2xy−15\)
عادةً ما تكون طريقة FOIL هي أسرع طريقة لضرب اثنين من الحدين، ولكنها تعمل فقط مع الحدين. يمكنك استخدام خاصية التوزيع للعثور على حاصل ضرب أي من كثيري الحدود. الطريقة الأخرى التي تعمل مع جميع كثيرات الحدود هي الطريقة الرأسية. إنها تشبه إلى حد كبير الطريقة التي تستخدمها لضرب الأرقام الصحيحة. انظر بعناية إلى هذا المثال لضرب الأرقام المكونة من رقمين.

الآن سنقوم بتطبيق نفس الطريقة لضرب اثنين من الحدين.
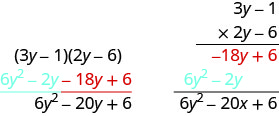
اضرب باستخدام الطريقة الرأسية:\((3y−1)(2y−6)\).
- إجابة
-
لا يهم أي معادلة ذات حدين توضع في الأعلى.
\ (\ ابدأ {محاذاة *} و &\ رباعي\؛\؛\؛ 3y - 1\\ [4pt]
و\\\ تسطير {\ رباعي\ مرات\؛ 2y-6}\\ [4pt]
و\ text {اضرب} 3y-1\ النص {بواسطة} -6. &\ رباعية -18 عامًا+ 6 &\ نص {منتج جزئي}\\ [4pt]
و\ text {اضرب} 3y-1\ النص {بواسطة} 2y. &\ تسطير {6y^2 - 2y} &\ text {منتج جزئي}\\ [4pt]
و\ text {أضف مصطلحات مماثلة.} & & & 6y^2 - 20 سنة + 6\ النهاية {محاذاة}\)لاحظ أن المنتجات الجزئية هي نفس المصطلحات في طريقة FOIL.
اضرب باستخدام الطريقة الرأسية:\((5m−7)(3m−6)\).
- إجابة
-
\(15m^2−51m+42\)
اضرب باستخدام الطريقة الرأسية:\((6b−5)(7b−3)\).
- إجابة
-
\(42b^2−53b+15\)
لقد استخدمنا الآن ثلاث طرق لضرب المقادير ذات الحدين. تأكد من ممارسة كل طريقة، وحاول تحديد الطريقة التي تفضلها. يتم سرد الطرق هنا معًا لمساعدتك على تذكرها.
لضرب المقادير ذات الحدين، استخدم:
- خاصية التوزيع
- طريقة فويل
- الطريقة الرأسية
ضرب كثير الحدود في كثير الحدود
لقد قمنا بضرب وحيدات الحد في وحيدات الحد بكثيرات الحدود وثنائية الحدين في الحدين. نحن الآن على استعداد لضرب كثير الحدود في كثير الحدود. تذكر أن FOIL لن تعمل في هذه الحالة، ولكن يمكننا استخدام خاصية التوزيع أو الطريقة الرأسية.
اضرب\((b+3)(2b^2−5b+8)\) باستخدام ⓐ خاصية التوزيع و ⓑ الطريقة الرأسية.
- إجابة
-
أ.
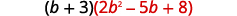
قم بالتوزيع. 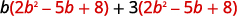
اضرب. 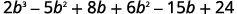
اجمع بين المصطلحات المتشابهة. 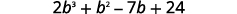
ب- من الأسهل وضع متعدد الحدود بمصطلحات أقل في الأسفل لأننا نحصل على عدد أقل من المنتجات الجزئية بهذه الطريقة.
\((2b^2−5b+8)\)اضرب في 3.
\((2b^2−5b+8)\)اضرب في\(b\).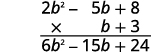
أضف مصطلحات الإعجاب. 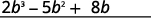
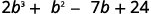
اضرب\((y−3)(y^2−5y+2)\) باستخدام ⓐ خاصية التوزيع و ⓑ الطريقة الرأسية.
- إجابة
-
أ.\(y^3−8y^2+17y−6\)
ب.\(y^3−8y^2+17y−6\)
اضرب\((x+4)(2x^2−3x+5)\) باستخدام أ) خاصية التوزيع و ب) الطريقة الرأسية.
- إجابة
-
أ. و ب.\(2x^3+5x^2−7x+20\)
لقد رأينا الآن طريقتين يمكنك استخدامهما لضرب كثير الحدود في كثير الحدود. بعد ممارسة كل طريقة، ربما ستجد أنك تفضل طريقة واحدة على الأخرى. نسرد كلتا الطريقتين مدرجتين هنا، لسهولة الرجوع إليها.
لضرب ثلاثية في معادلة ذات حدين، استخدم:
- خاصية التوزيع
- الطريقة الرأسية
ضاعف المنتجات الخاصة
يحب علماء الرياضيات البحث عن الأنماط التي ستجعل عملهم أسهل. وخير مثال على ذلك هو تربيع المعادلات ذات الحدين. بينما يمكنك دائمًا الحصول على المنتج عن طريق كتابة المعادلة ذات الحدين مرتين وضربهما، إلا أنه لا يوجد الكثير من العمل الذي يتعين عليك القيام به إذا تعلمت استخدام النمط. لنبدأ بالنظر إلى ثلاثة أمثلة والبحث عن النمط.
انظر إلى هذه النتائج. هل ترى أي أنماط؟
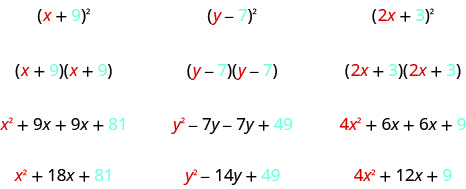
ماذا عن عدد المصطلحات؟ في كل مثال، قمنا بتربيع معادلة ذات حدين وكانت النتيجة ثلاثية الحدود.
\[(a+b)^2=\text{___}+\text{___}+\text{___} \nonumber\]
انظر الآن إلى الفصل الأول في كل نتيجة. من أين أتت؟
المصطلح الأول هو نتاج المصطلحات الأولى لكل معادلة ذات حدين. نظرًا لأن الحدين متطابقان، فهو مجرد مربع المصطلح الأول!
\[(a+b)^2=a^2+\text{___}+\text{___} \nonumber\]
للحصول على الفصل الأول للمنتج، قم بتربيع المصطلح الأول.
من أين جاء الفصل الأخير؟ انظر إلى الأمثلة وابحث عن النمط.
المصطلح الأخير هو نتاج المصطلحات الأخيرة، وهو مربع الفصل الأخير.
\[(a+b)^2=\text{___}+\text{___}+b^2 \nonumber\]
للحصول على الفصل الأخير من المنتج، ضع مربع المصطلح الأخير.
أخيرًا، انظر إلى المدى المتوسط. لاحظ أنه جاء من إضافة المصطلحين «الخارجي» و «الداخلي» - وكلاهما متشابهان! لذا فإن الحد الأوسط هو ضعف ناتج مصطلحي المعادلة ذات الحدين.
\[(a+b)^2=\text{___}+2ab+\text{___} \nonumber\]
\[(a−b)^2=\text{___}−2ab+\text{___} \nonumber\]
للحصول على المدى المتوسط للمنتج، اضرب المصطلحات وضاعف منتجها.
وضع كل ذلك معًا:
إذا كانت a و b أرقامًا حقيقية،

لتربيع الحد ذي الحدين، قم بتربيع الحد الأول، ومربع المصطلح الأخير، ومضاعفة الناتج.
اضرب: أ.\((x+5)^2\) ب\((2x−3y)^2\).
- إجابة
-
أ.
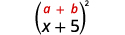
مربع الفصل الدراسي الأول. 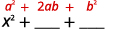
مربع الفصل الأخير. 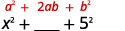
ضاعف منتجهم. 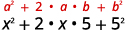
قم بالتبسيط. 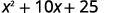
ب.
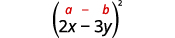
استخدم النمط. 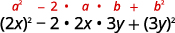
قم بالتبسيط. 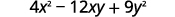
اضرب: أ.\((x+9)^2\) ب\((2c−d)^2\).
- إجابة
-
أ.\(x^2+18x+81\)
ب.\(4c^2−4cd+d^2\)
اضرب: أ.\((y+11)^2\) ب\((4x−5y)^2\).
- إجابة
-
أ.\(y^2+22y+121\)
ب.\(16x^2−40xy+25y^2\)
لقد رأينا للتو نمطًا لتربيع المقادير ذات الحدين يمكننا استخدامه لتسهيل ضرب بعض المقادير ذات الحدين. وبالمثل، هناك نمط لمنتج آخر من المعادلات ذات الحدين. ولكن قبل أن نصل إليها، نحتاج إلى تقديم بعض المفردات.
زوج من الحدين لكل منهما نفس الحد الأول ونفس الحد الأخير، ولكن الواحد هو المجموع والآخر هو الفرق يسمى الزوج المترافق وهو من الشكل\((a−b)\)،\((a+b)\).
الزوج المترافق عبارة عن وحدين من الشكل
\[(a−b), (a+b). \nonumber\]
لكل زوج من الحدين نفس الحد الأول ونفس الحد الأخير، ولكن أحد الحدين هو المجموع والآخر هو الفرق.
هناك نمط جميل للعثور على منتج المترافقات. يمكنك بالطبع ببساطة الحصول على المنتج، ولكن استخدام النمط يجعل عملك أسهل. دعونا نبحث عن النمط باستخدام FOIL لمضاعفة بعض الأزواج المترافقة.
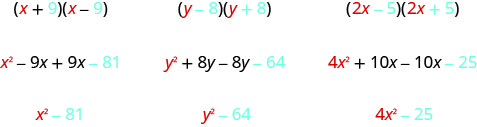
ماذا تلاحظ عن المنتجات؟
منتج الحدين هو أيضًا معادلة ذات حدين! معظم المنتجات الناتجة عن FOIL كانت ثلاثية الأبعاد.
كل مصطلح أول هو نتاج المصطلحات الأولى من الحدين، وبما أنها متطابقة فهو مربع المصطلح الأول.
\[(a+b)(a−b)=a^2−\text{___} \nonumber\]
للحصول على الفصل الدراسي الأول، قم بتربيع الفصل الدراسي الأول.
المصطلح الأخير جاء من ضرب الحدود الأخيرة، مربع الحد الأخير.
\[(a+b)(a−b)=a^2−b^2 \nonumber\]
للحصول على الفصل الدراسي الأخير، قم بتربيع الفصل الأخير.
لماذا لا يوجد مصطلح متوسط؟ لاحظ أن الحدين المتوسطين اللذين تحصل عليهما من FOIL يتحدان إلى 0 في كل حالة، نتيجة الجمع الواحدة والطرح الواحد.
يكون منتج الاقتران دائمًا بالشكل\(a^2−b^2\). وهذا ما يسمى بفرق المربعات.
هذا يؤدي إلى النمط:
إذا كانت a و b أرقامًا حقيقية،

يُطلق على المنتج اسم اختلاف المربعات.
لضرب المترادفات، قم بمربع الحد الأول، ومربع الحد الأخير، وكتابته في صورة فرق بين المربعات.
اضرب باستخدام ناتج نمط المترافقات: a.\((2x+5)(2x−5)\) b\((5m−9n)(5m+9n)\).
- إجابة
-
أ.
هل يترافق الحدان؟ 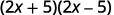
إنه نتاج المترافقة. 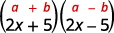
مربع الفصل الأول، 2x.2x. 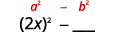
مربع الفصل الأخير، 5.5. 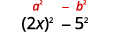
قم بالتبسيط. المنتج هو اختلاف المربعات. 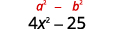
ب.
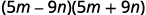
هذا يناسب النمط. 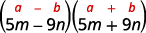
استخدم النمط. 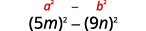
قم بالتبسيط. 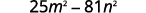
اضرب: أ.\((6x+5)(6x−5)\) ب\((4p−7q)(4p+7q)\).
- إجابة
-
أ.\(36x^2−25\)
ب.\(16p^2−49q^2\)
اضرب: أ.\((2x+7)(2x−7)\) ب\((3x−y)(3x+y)\).
- إجابة
-
أ.\(4x^2−49\) ب.\(9x^2−y^2\)
لقد قمنا للتو بتطوير أنماط منتجات خاصة للمربعات ذات الحدين ولمنتج المترافقات. تبدو المنتجات متشابهة، لذلك من المهم التعرف على الوقت المناسب لاستخدام كل من هذه الأنماط وملاحظة مدى اختلافها. انظر إلى النموذجين معًا ولاحظ أوجه التشابه والاختلاف بينهما.
| مربعات ذات حدين | منتج من منتجات المترافقة |
|---|---|
| \((a+b)^2=a^2+2ab+b^2\) | \((a−b)(a+b)=a^2−b^2\) |
| \((a−b)^2=a^2−2ab+b^2\) | |
| • تربيع معادلة ذات حدين | • ضرب المترادفات |
| • المنتج عبارة عن تركيبة ثلاثية | • المنتج ذو حدين. |
| • المصطلحات الداخلية والخارجية مع FOIL هي نفسها. | • المصطلحات الداخلية والخارجية مع FOIL هي الأضداد. |
| • المدى المتوسط هو ضعف نتاج المصطلحات | • لا يوجد مصطلح متوسط. |
اختر النمط المناسب واستخدمه للعثور على المنتج:
أ.\((2x−3)(2x+3)\) ب.\((8x-5)^2\) ج.\((6m+7)^2\) د\((5x−6)(6x+5)\).
- إجابة
-
أ.\((2x−3)(2x+3)\)
هذه هي المرادفات. لديهم نفس الأرقام الأولى، ونفس الأرقام الأخيرة، وأحد الحدين هو المجموع والآخر هو الفرق. يناسب نمط منتج المترافقات.
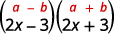
استخدم النمط. 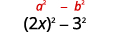
قم بالتبسيط. 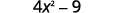
ب.\((8x−5)^2\)
يُطلب منا وضع معادلة ذات حدين. يناسب نمط المربعات ذات الحدين.
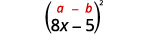
استخدم النمط. 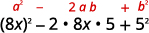
قم بالتبسيط. 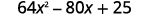
ج.\((6m+7)^2\)
مرة أخرى، سنقوم بتربيع معادلة ذات حدين حتى نستخدم نمط المربعات ذات الحدين.
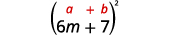
استخدم النمط. 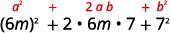
قم بالتبسيط. 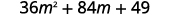
د.\((5x−6)(6x+5)\)
هذا المنتج لا يناسب الأنماط، لذلك سنستخدم FOIL.
\(\begin{array} {ll} {} &{(5x−6)(6x+5)} \\ {\text{Use FOIL.}} & {30x^2+25x−36x−30} \\ {\text{Simplify.}} & {30x^2−11x−30} \\ \end{array}\)
اختر النمط المناسب واستخدمه للعثور على المنتج:
أ.\((9b−2)(2b+9)\) ب.\((9p−4)^2\) ج.\((7y+1)^2\) د\((4r−3)(4r+3)\).
- إجابة
-
أ. الفويل؛\(18b^2+77b−18\)
ب. المربعات ذات الحدين؛\(81p^2−72p+16\)
ج. المربعات ذات الحدين؛\(49y^2+14y+1\)
د. حاصل ضرب المترافقات؛\(16r^2−9\)
اختر النمط المناسب واستخدمه للعثور على المنتج:
أ.\((6x+7)^2\) ب.\((3x−4)(3x+4)\) ج.\((2x−5)(5x−2)\) د\((6n−1)^2\).
- إجابة
-
أ. المربعات ذات الحدين؛\(36x^2+84x+49\) ب. حاصل ضرب المترادفات؛\(9x^2−16\) ج. الفويل؛\(10x^2−29x+10\) د. المربعات ذات الحدين؛\(36n^2−12n+1\)
ضرب دوال كثيرة الحدود
مثلما يمكن ضرب كثيرات الحدود، يمكن أيضًا ضرب الدوال متعددة الحدود.
للوظائف\(f(x)\) و\(g(x)\)،
\[(f·g)(x)=f(x)·g(x)\]
للوظائف\(f(x)=x+2\) وابحث\(g(x)=x^2−3x−4\) عن:
- \((f·g)(x)\)
- \((f·g)(2)\).
- إجابة
-
أ.
\(\begin{array} {ll} {} &{(f·g)(x)=f(x)·g(x)} \\ {\text{Substitute for } f(x) \text{ and } g(x)} &{(f·g)(x)=(x+2)(x^2−3x−4)} \\ {\text{Multiply the polynomials.}} &{(f·g)(x)=x(x^2−3x−4)+2(x^2−3x−4)} \\ {\text{Distribute.}} &{(f·g)(x)=x3−3x^2−4x+2x^2−6x−8} \\ {\text{Combine like terms.}} &{(f·g)(x)=x3−x^2−10x−8} \\ \end{array}\)
ب. في الجزء أ. وجدنا\((f·g)(x)\) ويطلب منا الآن العثور عليه\((f·g)(2)\).
\(\begin{array} {ll} {} &{(f·g)(x)=x^3−x^2−10x−8} \\ {\text{To find }(f·g)(2), \text{ substitute } x=2.} &{(f·g)(2)=2^3−2^2−10·2−8} \\ {} &{(f·g)(2)=8−4−20−8} \\ {} &{(f·g)(2)=−24} \\ \end{array}\)
للوظائف\(f(x)=x−5\) وابحث\(g(x)=x^2−2x+3\)
- \((f·g)(x)\)
- \((f·g)(2)\).
- الإجابة أ
-
\((f·g)(x)=x^3−7x^2+13x−15\)
- الإجابة ب
-
\((f·g)(2)=−9\)
للوظائف\(f(x)=x−7\) وابحث\(g(x)=x^2+8x+4\)
- \((f·g)(x)\)
- \((f·g)(2)\).
- الإجابة أ
-
\((f·g)(x)=x^3+x^2−52x−28\)
- الإجابة أ
-
\((f·g)(2)=−120\)
يمكنك الوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات وممارسة إضافية بضرب كثيرات الحدود.
- مقدمة للمنتجات الخاصة ذات الحدين
المفاهيم الرئيسية
- كيفية استخدام طريقة FOIL لضرب اثنين من الحدين.
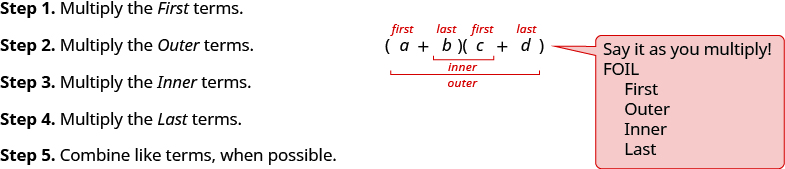
- ضرب عددين: لضرب المقادير ذات الحدين، استخدم:
- خاصية التوزيع
- طريقة فويل
- ضرب كثير الحدود في كثير الحدود: لضرب ثلاثية الحدود في معادلة ذات حدين، استخدم:
- خاصية التوزيع
- الطريقة الرأسية
- نمط المربعات ذات الحدين
إذا كانت a و b أعدادًا حقيقية،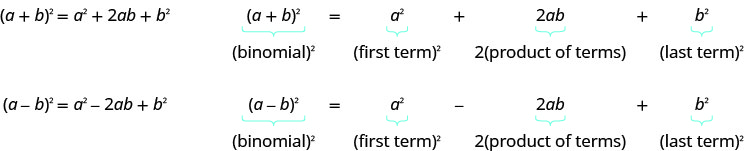
- حاصل ضرب نمط المترافقات
إذا كانت a و b أرقامًا
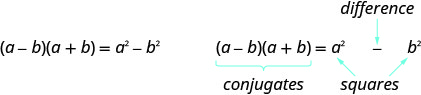
حقيقية يُطلق على المنتج اسم فرق المربعات.
لضرب المترادفات، قم بمربع الحد الأول، ومربع الحد الأخير، وكتابته في صورة فرق بين المربعات. - مقارنة أنماط المنتجات الخاصة
مربعات ذات حدين منتج من منتجات المترافقة \((a+b)^2=a^2+2ab+b^2\) \((a−b)^2=a^2−2ab+b^2\) \((a−b)(a+b)=a^2−b^2\) • تربيع معادلة ذات حدين • ضرب المترادفات • المنتج عبارة عن تركيبة ثلاثية • المنتج ذو حدين. • المصطلحات الداخلية والخارجية مع FOIL هي نفسها. • المصطلحات الداخلية والخارجية مع FOIL هي الأضداد. • المدى المتوسط هو ضعف نتاج المصطلحات • لا يوجد مصطلح متوسط. - ضرب الدوال كثيرة الحدود:
- للوظائف\(f(x)\) و\(g(x)\)،
\[(f⋅g)(x)=f(x)⋅g(x) \nonumber\]
- للوظائف\(f(x)\) و\(g(x)\)،
مسرد المصطلحات
- زوج مترافق
- الزوج المترافق عبارة عن وحدين من الشكل\((a−b)\) و\((a+b)\). لكل زوج من الحدين نفس الحد الأول ونفس الحد الأخير، ولكن أحد الحدين هو المجموع والآخر هو الفرق.


