5.2: جمع وطرح كثيرات الحدود
- Page ID
- 201512
في نهاية هذا القسم، ستكون قادرًا على:
- تحديد درجة كثيرات الحدود
- جمع وطرح كثيرات الحدود
- إيجاد قيمة دالة كثيرة الحدود لقيمة معطاة
- جمع وطرح دوال كثيرة الحدود
تحديد درجة كثيرات الحدود
لقد تعلمنا أن المصطلح ثابت أو نتاج ثابت ومتغير واحد أو أكثر. الحد الأحادي هو تعبير جبري بحد واحد. عندما يكون من النموذج\(ax^m\)، حيث\(a\) يكون ثابتًا\(m\) وهو رقم صحيح، يُطلق عليه اسم أحادي الحد في متغير واحد. بعض الأمثلة على أحادية الحد في متغير واحد هي. يمكن أن تحتوي Monomials أيضًا على أكثر من متغير واحد مثل و\(−4a^2b^3c^2.\)
الحد الأحادي هو تعبير جبري بحد واحد. الحد الأحادي في متغير واحد هو مصطلح النموذج\(ax^m\)، حيث\(a\) يكون ثابتًا\(m\) وهو رقم صحيح.
يُعد العدد الأحادي، أو وحيدين أو أكثر من وحيدات الحد معًا بالجمع أو الطرح، عددًا كبيرًا من الحدود. تحتوي بعض كثيرات الحدود على أسماء خاصة، استنادًا إلى عدد المصطلحات. الحد الأحادي هو متعدد الحدود بمصطلح واحد بالضبط. تحتوي المعادلة ذات الحدين على مصطلحين بالضبط، بينما تحتوي المعادلة الثلاثية على ثلاثة مصطلحات بالضبط. لا توجد أسماء خاصة لكثيرات الحدود بأكثر من ثلاثة مصطلحات.
- كثير الحدود —الحد الأحادي، أو الحد الجبري أو أكثر بالجمع بالجمع أو الطرح هو كثير الحدود.
- أحادي الحد - يُطلق على كثير الحدود الذي يحتوي على مصطلح واحد بالضبط اسم أحادي الحد.
- المعادلة ذات الحدين - يُطلق على كثير الحدود الذي يحتوي على حدين بالضبط اسم ذات حدين.
- ثلاثي الحدود - يُطلق على كثير الحدود الذي يحتوي على ثلاثة حدود بالضبط اسم ثلاثي الحدود.
فيما يلي بعض الأمثلة لكثيرات الحدود.
| متعدد الحدود | \(y+1\) | \(4a^2−7ab+2b^2\) | \(4x^4+x^3+8x^2−9x+1\) | |
|---|---|---|---|---|
| أحادية الحد | \(14\) | \(8y^2\) | \(−9x^3y^5\) | \(−13a^3b^2c\) |
| معادلة ذات حدين | \(a+7ba+7b\) | \(4x^2−y^2\) | \(y^2−16\) | \(3p^3q−9p^2q\) |
| معادلة ثلاثية الحدود | \(x^2−7x+12\) | \(9m^2+2mn−8n^2\) | \(6k^4−k^3+8k\) | \(z^4+3z^2−1\) |
لاحظ أن كل رقم أحادي وذي حدين وثلاثي الحدود هو أيضًا كثير الحدود. إنهم مجرد أعضاء مميزين في «عائلة» كثيرات الحدود وبالتالي لديهم أسماء خاصة. نحن نستخدم الكلمات أحادية الحدين وذات الحدين وثلاثية الحدود عند الإشارة إلى هذه الكثيرات الخاصة ونطلق فقط على جميع كثيرات الحدود الباقية.
يتم تحديد درجة متعدد الحدود ودرجة شروطه من خلال أسس المتغير. إن الحد الأحادي الذي لا يحتوي على متغير، مجرد ثابت، هو حالة خاصة. درجة الثابت هي 0.
- درجة المصطلح هي مجموع أسس المتغيرات الخاصة به.
- درجة الثابت هي 0.
- درجة تعدد الحدود هي أعلى درجة من جميع مصطلحاتها.
دعونا نرى كيف يعمل هذا من خلال النظر إلى العديد من كثيرات الحدود. سنأخذ الأمر خطوة بخطوة، بدءًا من الحدود الأحادية، ثم ننتقل إلى كثيرات الحدود بمزيد من المصطلحات. لنبدأ بالنظر إلى مونوميال. \(8ab^2\)يحتوي الحد الأحادي على متغيرين\(a\) و\(b\). للعثور على الدرجة، نحتاج إلى إيجاد مجموع الأسس. لا يحتوي المتغير a على أس مكتوب، ولكن تذكر أن هذا يعني أن الأس هو 1. الأس لـ\(b\) هو 2. مجموع الأسس، 1+2,1+2، هو 3، وبالتالي فإن الدرجة هي 3.

فيما يلي بعض الأمثلة الإضافية.

يكون التعامل مع كثيرات الحدود أسهل عندما تقوم بإدراج المصطلحات بترتيب تنازلي للدرجات. عندما تتم كتابة كثير الحدود بهذه الطريقة، يُقال إنها في الشكل القياسي لكثيرات الحدود. اعتد على كتابة المصطلح بأعلى درجة أولاً.
حدِّد ما إذا كان كل كثير الحدود عبارة عن معادلة أحادية أو ذات حدين أو ثلاثية الحدود أو غيرها من كثيرات الحدود. ثم أوجد درجة كل كثير الحدود.
- \(7y2−5y+3\)
- \(−2a^4b^2\)
- \(3x5−4x3−6x2+x−8\)
- \(2y−8xy^3\)
- \(15\)
- إجابة
-
متعدد الحدود عدد المصطلحات النوع درجة المصطلحات درجة تعدد الحدود ⓐ \(7y^2−5y+3\) 3 معادلة ثلاثية الحدود 2، 1، 0 2 ⓑ \(−2a^4b^2−2a^4b^2\) 1 أحادية الحد 4، 2 6 ⓒ \(3x5−4x3−6x2+x−8\) 5 متعدد الحدود 5، 3، 2، 1، 0 5 ⓓ \(2y−8xy^3\) 2 معادلة ذات حدين 1، 4 4 ⓔ \(15\) 1 أحادية الحد 0 0
حدِّد ما إذا كان كل كثير الحدود عبارة عن معادلة أحادية أو ذات حدين أو ثلاثية الحدود أو غيرها من كثيرات الحدود. ثم أوجد درجة كل كثير الحدود.
- \(−5\)
- \(8y^3−7y^2−y−3\)
- \(−3x^2y−5xy+9xy^3\)
- \(81m^2−4n^2\)
- \(−3x^6y^3z\)
- الإجابة أ
-
أحادي الحد، 0
- الإجابة ب
-
متعدد الحدود، 3
- الإجابة ج
-
ثلاثي الحدود، 3
- الإجابة د
-
معادلة ذات حدين، 2
- الإجابة ب
-
أحادية الحد، 10
حدِّد ما إذا كان كل كثير الحدود عبارة عن معادلة أحادية أو ذات حدين أو ثلاثية الحدود أو غيرها من كثيرات الحدود. ثم أوجد درجة كل كثير الحدود.
- \(64k^3−8\)
- \(9m^3+4m^2−2\)
- \(56\)
- \(8a^4−7a^3b−6a^2b^2−4ab^3+7b^4\)
- \(-p^4q^3\)
- إجابة
-
ⓐ ذو حدين، 3 ⓑ ثلاثي الحدود، 3 ⓒ أحادي الحد، 0 ⓓ متعدد الحدود، 4 ⓔ أحادي الحد، 7
جمع وطرح كثيرات الحدود
لقد تعلمنا كيفية تبسيط التعبيرات من خلال الجمع بين المصطلحات المتشابهة. تذكر أن المصطلحات المتشابهة يجب أن تحتوي على نفس المتغيرات بنفس الأس. نظرًا لأن القيم الأحادية عبارة عن مصطلحات، فإن جمع وحيدات الحد وطرحها يماثل الجمع بين المصطلحات المتشابهة. إذا كانت القيم الأحادية تشبه المصطلحات، فإننا ندمجها فقط عن طريق إضافة المعاملات أو طرحها.
إضافة أو طرح:
- \(25y^2+15y^2\)
- \(16pq^3−(−7pq^3)\).
- الإجابة أ
-
\( \begin{array} {ll} {} &{25y^2+15y^2} \\ {\text{Combine like terms.}} &{40y^2} \\ \end{array} \nonumber \)
- الإجابة ب
-
\( \begin{array} {ll} {} &{16pq^3−(−7pq^3)} \\ {\text{Combine like terms.}} &{23pq^3} \\ \end{array} \nonumber \)
إضافة أو طرح:
- \(12q^2+9q^2\)
- \(8mn^3−(−5mn^3)\).
- إجابة
-
ⓐ\(21q^2\) ⓑ\(13mn^3\)
إضافة أو طرح:
- \(−15c^2+8c^2\)
- \(−15y^2z^3−(−5y^2z^3)\)
- إجابة
-
ⓐ\(−7c^2\) ⓑ\(−10y^2z^3\)
تذكر أن المصطلحات المتشابهة يجب أن تحتوي على نفس المتغيرات بنفس الأسس.
قم بالتبسيط:
- \(a^2+7b^2−6a^2\)
- \(u^2v+5u^2−3v^2\)
- إجابة
-
ⓐ اجمع بين المصطلحات المتشابهة.
\(a^2+7b^2−6a^2 \;=\; −5a^2+7b^2\)ⓑ لا توجد مصطلحات مماثلة للدمج. في هذه الحالة، لا يتغير متعدد الحدود.
\(u^2v+5u^2−3v^2\)
إضافة:
- \(8y^2+3z^2−3y^2\)
- \(m^2n^2−8m^2+4n^2\)
- إجابة
-
ⓐ\(5y^2+3z^2\)
ⓑ\(m^2n^2−8m^2+4n^2\)
إضافة:
- \(3m^2+n^2−7m^2\)
- \(pq^2−6p−5q^2\)
- إجابة
-
ⓐ\(−4m^2+n^2\)
ⓑ\(pq^2−6p−5q^2\)
يمكننا التفكير في جمع وطرح كثيرات الحدود كمجرد جمع وطرح سلسلة من وحيدات الحد. ابحث عن المصطلحات المتشابهة - تلك التي لها نفس المتغيرات ونفس الأس. تسمح لنا خاصية الاستبدال بإعادة ترتيب المصطلحات لتجميع المصطلحات المتشابهة معًا.
ابحث عن المبلغ:\((7y^2−2y+9)\;+\;(4y^2−8y−7)\).
- إجابة
-
\ (\ ابدأ {align*} &\ text {حدد المصطلحات المشابهة.} & (\ تسطير {\ تسطير {\ تسطير {7y^2}} −\ تسطير {2y} +9) + (\ تسطير {\ تسطير {4y^2}}} −\ تسطير {8y} −7)\\ [6pt]
\\\ النص {أعد الكتابة بدون الأقواس،}\
\\\ النص {إعادة الترتيب للحصول على المصطلحات المتشابهة معًا.} &\ تسطير {\ تسطير {7y^2+4y^2}} −\ تسطير {2y−8y}} +9−7\\ [6pt]
و\ النص {اجمع المصطلحات المتشابهة.} & & & 11y^2−10y+2\ النهاية {محاذاة}\)
ابحث عن المبلغ:\( (7x^2−4x+5)\;+\;(x^2−7x+3)\)
- إجابة
-
\(8x^2−11x+8\)
ابحث عن المبلغ:\((14y^2+6y−4)\;+\;(3y^2+8y+5)\)
- إجابة
-
\(17y^2+14y+1\)
كن حذرًا عند استخدام العلامات أثناء التوزيع أثناء طرح كثيرات الحدود في المثال التالي.
ابحث عن الفرق:\((9w^2−7w+5)\;−\;(2w^2−4)\)
- إجابة
-
\ (\ ابدأ {align*} & & (9w ^2−7w+5)\; −\; (2w^2−4)\\ [6pt]
و\ النص {توزيع المصطلحات المتشابهة وتحديدها.} &\ تسطير {\ تسطير {9w^2}} −\ تسطير {7w} +5-\ تسطير {\ تسطير {2w^2}} +4\\ [6pt]
و\ النص {إعادة ترتيب الشروط.} &\ تسطير {\ تسطير {9w^2-2w ^ 2}} −\ تسطير {7w} +5+4\\ [6pt]
و\ text {اجمع المصطلحات المتشابهة.} & & & 7w ^ 2−7w+9\ النهاية {align*}\)
ابحث عن الفرق:\((8x^2+3x−19)\;−\;(7x^2−14)\)
- إجابة
-
\(x^2+3x−5\)
ابحث عن الفرق:\((9b^2−5b−4)\;−\;(3b^2−5b−7)\)
- إجابة
-
\(6b^2+3\)
اطرح\((p^2+10pq−2q^2)\) من\((p^2+q^2)\).
- إجابة
-
\ (\ ابدأ {align*} & & (p^2+q^2)\; −\; (p^2+10pq−2q^2)\\ [6pt]
و\ text {توزيع المصطلحات المتشابهة وتحديدها.} &\ تسطير {\ تسطير {p^2}} +\ تسطير {q^2} -\ تسطير {\\ تسطير {p^2}} -10pq +\ تسطير {2q^2}\\ [6pt]
و\ النص {أعد ترتيب المصطلحات، مع وضع المصطلحات المتشابهة معًا.} &\ تسطير {\ تسطير {p^2-p^2}} −10pq +\ تسطير {q^2 + 2q^2}\\ [6pt]
و\ النص {اجمع المصطلحات المتشابهة.} & & −10pq+3q^2\ النهاية {align*}\)
اطرح\((a^2+5ab−6b^2)\) من\((a^2+b^2)\)
- إجابة
-
\(−5ab+7b^2\)
اطرح\((m^2−7mn−3n^2)\) من\((m^2+n^2)\).
- إجابة
-
7 مليمتر+4 نانومتر ^ 2
ابحث عن المبلغ:\((u^2−6uv+5v^2)\;+\;(3u^2+2uv)\)
- إجابة
-
\ (\ ابدأ {align*} & & (u^2−6uv+5v^2)\; +\; (3u^2+2uv)\\ [6pt]
و\ text {توزيع وتعريف المصطلحات المتشابهة.} &\ تسطير {\ تسطير {u^2}} -\ تسطير {6uv} +5v^2+\ تسطير {\ تسطير {3u^2}} +\ تسطير {2uv}\\ [6pt]
و\\ النص {أعد ترتيب المصطلحات لوضع المصطلحات المتشابهة معًا.} &\ تسطير {\ تسطير {u^2}} +\ تسطير {\\ تسطير {3u^2}} -\ تسطير {6uv} +\ تسطير {2uv} +5v^2\ [6pt]
و\ النص {اجمع المصطلحات المتشابهة.} & & & 4u ^2−4uv+5v ^2\ النهاية {align*}\)
ابحث عن المبلغ:\((3x^2−4xy+5y^2)\;+\;(2x^2−xy)\)
- إجابة
-
\(5x^2−5xy+5y^2\)
ابحث عن المبلغ:\((2x^2−3xy−2y^2)\;+\;(5x^2−3xy)\)
- إجابة
-
\(7x^2−6xy−2y^2\)
عندما نجمع ونطرح أكثر من كثيرات الحدود، تكون العملية هي نفسها.
قم بالتبسيط:\((a^3−a^2b)\;−\;(ab^2+b^3)\;+\;(a^2b+ab^2)\)
- إجابة
-
\ (\ ابدأ {محاذاة *} & & (أ ^3−أ ^2b)\; −\; (ab^2+b^3)\\;\\; (أ ^2b+ab^2)\\ [6pt]
\\ [6pt]
و\ النص {التوزيع} و ^3−a^2b − ab^2\\\ text {أعد ترتيب المصطلحات لتجميع المصطلحات المتشابهة معًا.} & & a ^3−a^2b + a ^2b− ab^2 + ab^2 - b^3\\ [6pt]
و\ text {اجمع المصطلحات المتشابهة.} & & ^3−b^3\ end {align*}\)
قم بالتبسيط:\((x^3−x^2y)\;−\;(xy^2+y^3)\;+\;(x^2y+xy^2)\)
- إجابة
-
\(x^3+y^3\)
قم بالتبسيط:\((p^3−p^2q)\;+\;(pq^2+q^3)\;−\;(p^2q+pq^2)\)
- إجابة
-
\(p^3−3p^2q+q^3\)
إيجاد قيمة دالة كثيرة الحدود لقيمة مُعطاة
الدالة كثيرة الحدود هي دالة مُعرَّفة بدالة كثيرة الحدود. على سبيل المثال،\(f(x)=x^2+5x+6\)\(g(x)=3x−4\) وهي دوال كثيرة الحدود، لأنها\(x^2+5x+6\)\(3x−4\) وكثيرات الحدود.
الدالة كثيرة الحدود هي دالة يتم تعريف قيم نطاقها بواسطة دالة كثيرة الحدود.
في الرسوم البيانية والدوال، حيث قدمنا الوظائف لأول مرة، تعلمنا أن تقييم الدالة يعني إيجاد قيمة قيمة قيمة معينة\(f(x)\) لـ\(x\). لتقييم دالة كثيرة الحدود، سنقوم باستبدال القيمة المعطاة للمتغير ثم تبسيطها باستخدام ترتيب العمليات.
بالنسبة للوظيفة،\(f(x)=5x^2−8x+4\) ابحث عن:
- \(f(4)\)
- \(f(−2)\)
- \(f(0)\).
- إجابة
-
ⓐ
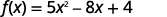
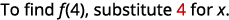
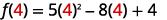
قم بتبسيط الأسس. 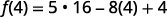
اضرب. 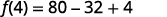
قم بالتبسيط. 
ⓑ
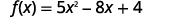
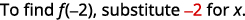
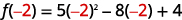
قم بتبسيط الأسس. 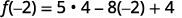
اضرب. 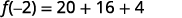
قم بالتبسيط. 
ⓒ
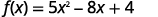
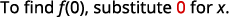
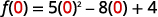
قم بتبسيط الأسس. 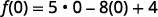
اضرب. 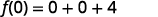
للحصول على الوظيفة\(f(x)=3x^2+2x−15\)، ابحث
- \(f(3)\)
- \(f(−5)\)
- \(f(0)\).
- إجابة
-
ⓐ 18 ⓑ 50 ⓒ\(−15\)
للحصول على الوظيفة\(g(x)=5x^2−x−4\)، ابحث
- \(g(−2)\)
- \(g(−1)\)
- \(g(0)\).
- إجابة
-
ⓐ 20 ⓑ 2 ⓒ\(−4\)
تُستخدم الدوال كثيرة الحدود المشابهة للدوال الموجودة في المثال التالي في العديد من الحقول لتحديد ارتفاع الجسم في وقت ما بعد إسقاطه في الهواء. يُستخدم كثير الحدود في الدالة التالية خصيصًا لإسقاط شيء من مسافة ٢٥٠ قدمًا.
\(h(t)=−16t^2+250\)تعطي الدالة كثيرة الحدود ارتفاع الكرة إلى ثوانٍ بعد إسقاطها من مبنى يبلغ ارتفاعه 250 قدمًا. أوجد الارتفاع بعد\(t=2\) ثوانٍ.
- إجابة
-
\( \begin{array} {ll} {} &{h(t)=−16t^2+250} \\ {} &{} \\ {\text{To find }h(2)\text{, substitute }t=2.} &{h(2)=−16(2)^2+250} \\ {\text{Simplify.}} &{h(2)=−16·4+250} \\ {} &{}\\ {\text{Simplify.}} &{h(2)=−64+250} \\ {} &{} \\ {\text{Simplify.}} &{h(2)=186} \\ {} &{\text{After 2 seconds the height of the ball is 186 feet.}} \\ \end{array} \nonumber \)
\(h(t)=−16t^2+150\)تعطي الدالة متعددة الحدود ارتفاع الحجر بعد ثوانٍ من إسقاطه من جرف يبلغ ارتفاعه 150 قدمًا. ابحث عن الارتفاع بعد\(t=0\) ثوانٍ (الارتفاع الأولي للكائن).
- إجابة
-
الارتفاع هو\(150\) القدمين.
\(h(t)=−16t^2+175\)تعطي الدالة كثيرة الحدود ارتفاع الكرة إلى ثوانٍ بعد إسقاطها من جسر يبلغ ارتفاعه 175 قدمًا. أوجد الارتفاع بعد\(t=3\) ثوانٍ.
- إجابة
-
الارتفاع هو\(31\) القدمين.
جمع وطرح دوال كثيرة الحدود
ومثلما يمكن إضافة كثيرات الحدود وطرحها، يمكن أيضًا إضافة دوال كثيرة الحدود وطرحها.
للوظائف\(f(x)\) و\(g(x)\)،
\[(f+g)(x)=f(x)+g(x)\]
\[(f−g)(x)=f(x)−g(x)\]
للوظائف\(f(x)=3x^2−5x+7\) وابحث\(g(x)=x^2−4x−3\) عن:
- \((f+g)(x)\)
- \((f+g)(3)\)
- \((f−g)(x)\)
- \((f−g)(−2)\).
- إجابة
-
ⓐ
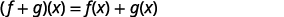
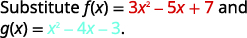
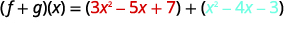
أعد الكتابة بدون الأقواس. 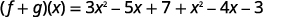
ضع المصطلحات المتشابهة معًا. 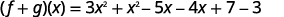
اجمع بين المصطلحات المتشابهة. 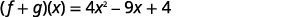
ⓑ وجدنا في الجزء (أ)\((f+g)(x)\) ويطلب منا الآن العثور عليه\((f+g)(3)\).
\( \begin{array} {ll} {} &{(f+g)(x)=4x^2−9x+4} \\ {} &{} \\ {\text{To find }(f+g)\space(3),\text{ substitute }x=3.} &{(f+g)(3)=4(3)^2−9·3+4} \\ {} &{} \\ {} &{(f+g)(3)=4·9−9·3+4} \\ {} &{} \\ {} &{(f+g)(3)=36−27+4} \\ \end{array} \nonumber \)
لاحظ أنه كان بإمكاننا العثور عليه\((f+g)(3)\) من خلال البحث أولاً عن القيم\(g(3)\) بشكل منفصل\(f(3)\) ثم إضافة النتائج.
ابحث\(f(3)\). 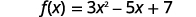

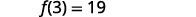
ابحث\(g(3)\). 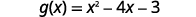
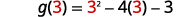
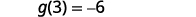
ابحث\((f+g)(3)\). 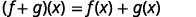
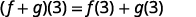
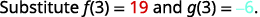

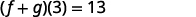
ⓒ
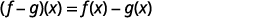
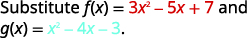
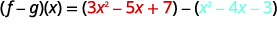
أعد الكتابة بدون الأقواس. 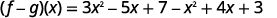
ضع المصطلحات المتشابهة معًا. 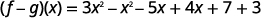
اجمع بين المصطلحات المتشابهة. 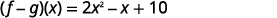
ⓓ
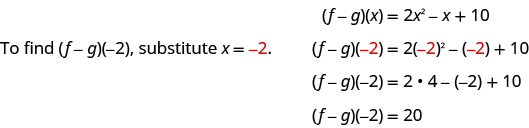
للوظائف\(f(x)=2x^2−4x+3\) وابحث\(g(x)=x^2−2x−6\) عن: ⓐ\((f+g)(x)\) ⓑ\((f+g)(3)\) ⓒ\((f−g)(x)\) ⓓ\((f−g)(−2)\).
- إجابة
-
ⓐ\((f+g)(x)=3x^2−6x−3\)
ⓑ\((f+g)(3)=6\)
ⓒ\((f−g)(x)=x^2−2x+9\)
ⓓ\((f−g)(−2)=17\)
للوظائف\(f(x)=5x^2−4x−1\) وابحث\(g(x)=x^2+3x+8\) عن ⓐ\((f+g)(x)\) ⓑ\((f+g)(3)\) ⓒ\((f−g)(x)\) ⓓ\((f−g)(−2)\).
- إجابة
-
ⓐ\((f+g)(x)=6x^2−x+7\)
ⓑ\((f+g)(3)=58\)
ⓒ\((f−g)(x)=4x^2−7x−9\)
ⓓ\((f−g)(−2)=21\)
يمكنك الوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات إضافية وممارسة جمع وطرح كثيرات الحدود.
- جمع وطرح كثيرات الحدود
المفاهيم الرئيسية
- أحادية الحد
- الحد الأحادي هو تعبير جبري بحد واحد.
- الحد الأحادي في متغير واحد هو حد الشكل axm، axm، حيث a هو ثابت و m هو رقم صحيح.
- كثيرات الحدود
- كثير الحدود —الحد الأحادي أو الحدين الجبريين أو أكثر بالجمع بالجمع أو الطرح هو كثير الحدود.
- أحادي الحد - يُطلق على كثير الحدود الذي يحتوي على مصطلح واحد بالضبط اسم أحادي الحد.
- المعادلة ذات الحدين - يُطلق على كثير الحدود الذي يحتوي على حدين بالضبط اسم ذات حدين.
- ثلاثي الحدود - يُطلق على كثير الحدود الذي يحتوي على ثلاثة حدود بالضبط اسم ثلاثي الحدود.
- درجة متعدد الحدود
- درجة المصطلح هي مجموع أسس المتغيرات الخاصة به.
- درجة الثابت هي 0.
- درجة تعدد الحدود هي أعلى درجة من جميع مصطلحاتها.
مسرد المصطلحات
- معادلة ذات حدين
- المعادلة ذات الحدين هي عبارة عن كثير الحدود بمصطلحين بالضبط.
- درجة ثابتة
- درجة أي ثابت هي 0.
- درجة متعددة الحدود
- درجة تعدد الحدود هي أعلى درجة من جميع مصطلحاتها.
- درجة المصطلح
- درجة المصطلح هي مجموع أسس المتغيرات الخاصة به.
- أحادية الحد
- الحد الأحادي هو تعبير جبري بحد واحد. الحد الأحادي في متغير واحد هو حد الشكل axm، axm، حيث a هو ثابت و m هو رقم صحيح.
- متعدد الحدود
- يُعد الحد الأحادي أو وحيدين أو أكثر معًا بالجمع أو الطرح عددًا كبيرًا من الحدود.
- الشكل القياسي لكثيرات الحدود
- يكون كثير الحدود في الشكل القياسي عندما تتم كتابة مصطلحات كثيرة الحدود بترتيب تنازلي للدرجات.
- ثلاثية الحدود
- والثلاثي هو كثير الحدود بثلاثة حدود بالضبط.
- دالة كثيرة الحدود
- الدالة كثيرة الحدود هي دالة يتم تعريف قيم نطاقها بواسطة دالة كثيرة الحدود.


