الفصل 4 تمارين المراجعة

Last updated
Save as PDF

Page ID: 201445

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

تمارين مراجعة الفصل

حل أنظمة المعادلات الخطية بمتغيرين

حدِّد ما إذا كان الزوج المُرتَّب حلًا لنظام المعادلات.

في التمارين التالية، حدد ما إذا كانت النقاط التالية عبارة عن حلول لنظام المعادلات المعطى.

1. $\left\{ \begin{array} {l} x+3y=−9\\2x−4y=12 \end{array} \right.$

ⓐ$(−3,−2)$
ⓑ$(0,−3)$

2. $\left\{ \begin{array} {l} x+y=8\\y=x−4 \end{array} \right.$

ⓐ$(6,2)$
ⓑ$(9,−1)$

إجابة: ⓐ نعم ⓑ لا

حل نظام المعادلات الخطية بالرسم البياني

في التمارين التالية، قم بحل أنظمة المعادلات التالية بالرسم البياني.

3. $\left\{ \begin{array} {l} 3x+y=6\\x+3y=−6 \end{array} \right.$

4. $\left\{ \begin{array} {l} x+4y=−1\\x=3 \end{array} \right.$

إجابة

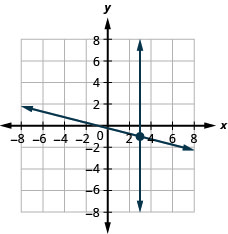
$يوضِّح الشكل التمثيل البياني للمعادلات x زائد أربعة في y يساوي ناقص واحد وx يساوي ثلاثة. يظهر خطان متقاطعان.$

$(3,−1)$

5. $\left\{ \begin{array} {l} 2x−y=5\\4x−2y=10 \end{array} \right.$

6. $\left\{ \begin{array} {l} −x+2y=4\\y=\frac{1}{2}x−3 \end{array} \right.$

إجابة

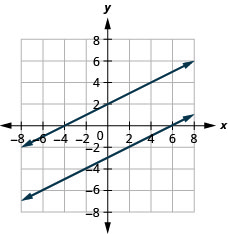
$يوضِّح الشكل الرسم البياني للمعادلات ناقص x زائد مرتين في y يساوي أربعة وy يساوي نصف x ناقص ثلاثة. يتم عرض خطين متوازيين.$

لا يوجد حل

في التمارين التالية، بدون رسم بياني، حدد عدد الحلول ثم صنف نظام المعادلات.

7. $\left\{ \begin{array} {l} y=\frac{2}{5}x+2\\−2x+5y=10 \end{array} \right.$

8. $\left\{ \begin{array} {l} 3x+2y=6\\y=−3x+4 \end{array} \right.$

إجابة: حل واحد، نظام ثابت، معادلات مستقلة

9. $\left\{ \begin{array} {l} 5x−4y=0\\y=\frac{5}{4}x−5 \end{array} \right.$

حل نظام المعادلات بالتعويض

في التمارين التالية، قم بحل أنظمة المعادلات عن طريق الاستبدال.

10. $\left\{ \begin{array} {l} 3x−2y=2\\y=\frac{1}{2}x+3 \end{array} \right.$

إجابة: $(4,5)$

11. $\left\{ \begin{array} {l} x−y=0\\2x+5y=−14 \end{array} \right.$

12. $\left\{ \begin{array} {l} y=−2x+7\\y=\frac{2}{3}x−1 \end{array} \right.$

إجابة: $(3,1)$

13. $\left\{ \begin{array} {l} y=−5x\\5x+y=6 \end{array} \right.$

14. $\left\{ \begin{array} {l} y=−\frac{1}{3}x+2\\x+3y=6 \end{array} \right.$

إجابة: العديد من الحلول بلا حدود

حل نظام المعادلات بالحذف

في التمارين التالية، حل أنظمة المعادلات بالحذف

15. $\left\{ \begin{array} {l} x+y=12\\x−y=−10 \end{array} \right.$

16. $\left\{ \begin{array} {l} 3x−8y=20\\x+3y=1 \end{array} \right.$

إجابة: $(4,−1)$

17. $\left\{ \begin{array} {l} 9x+4y=2\\5x+3y=5 \end{array} \right.$

18. $\left\{ \begin{array} {l} \frac{1}{3}x−\frac{1}{2}y=1\\ \frac{3}{4}x−y=\frac{5}{2} \end{array} \right.$

إجابة: $(6,2)$

19. $\left\{ \begin{array} {l} −x+3y=8\\2x−6y=−20 \end{array} \right.$

اختر الطريقة الأكثر ملاءمة لحل نظام المعادلات الخطية

في التمارين التالية، حدد ما إذا كان من الأنسب حل نظام المعادلات عن طريق الاستبدال أو الحذف.

20. $\left\{ \begin{array} {l} 6x−5y=27\\3x+10y=−24 \end{array} \right.$

إجابة: حذف

21. $\left\{ \begin{array} {l} y=3x−9\\4x−5y=23 \end{array} \right.$

حل تطبيقات باستخدام أنظمة المعادلات

حل تطبيقات الترجمة المباشرة

في التمارين التالية، قم بالترجمة إلى نظام المعادلات والحل.

22. تريد مولي أن تزرع 200 بصيلة في حديقتها، كلها قزحية وزنبق. إنها تريد أن تزرع ثلاثة أضعاف عدد زهور التوليب مثل القزحية. كم عدد القزحية وكم عدد زهور التوليب التي يجب أن تزرعها؟

إجابة: 50 قزحية و 150 زنبق

23. تم عرض وظائف على Ashanti من قبل شركتي هاتف. تدفع الشركة الأولى راتبًا قدره 22,000 دولار بالإضافة إلى عمولة قدرها 100 دولار لكل عقد يتم بيعه. يدفع الثاني راتبًا قدره 28000 دولار بالإضافة إلى عمولة قدرها 25 دولارًا لكل عقد تم بيعه. كم عدد العقود التي يجب بيعها لجعل الأجر الإجمالي هو نفسه؟

24. أمضى ليروي 20 دقيقة في الركض و 40 دقيقة في ركوب الدراجات وحرق 600 سعرة حرارية. في اليوم التالي، قام ليروي بتبديل الأوقات، حيث مارس 40 دقيقة من الركض و 20 دقيقة من ركوب الدراجات وحرق نفس العدد من السعرات الحرارية. كم عدد السعرات الحرارية التي تم حرقها لكل دقيقة من الركض وكم لكل دقيقة من ركوب الدراجات؟

إجابة: 10 سعرات حرارية للركض و 10 سعرات حرارية لركوب الدراجات

25. كان تروي وليزا يتسوقون لشراء اللوازم المدرسية. اشترى كل منهم كميات مختلفة من نفس دفتر الملاحظات والآلة الحاسبة. اشترى تروي أربعة أجهزة كمبيوتر محمولة وخمس حاسبات مقابل 116 دولارًا. اشترت ليزا جهازي كمبيوتر محمول وثلاث حاسبات مقابل 68 دولارًا. ابحث عن تكلفة كل كمبيوتر محمول وكل محرك أقراص محمول.

حل تطبيقات الهندسة

في التمارين التالية، قم بالترجمة إلى نظام المعادلات والحل.

26. الفرق بين زاويتين إضافيتين هو 58 درجة. أوجد قياسات الزوايا.

إجابة: 119، 61

27. زاويتان متكاملتان. قياس الزاوية الأكبر يزيد بمقدار خمسة أضعاف عن أربعة أضعاف قياس الزاوية الأصغر. أوجد قياسات كلتا الزاويتين.

28. يقل قياس إحدى الزوايا الصغيرة للمثلث الأيمن بمقدار 15 عن ضعف قياس الزاوية الصغيرة الأخرى. أوجد قياس كلتا الزاويتين.

إجابة: $35°$و$55°$

29. تُعلق بيكا إكليلًا زهريًا بطول 28 قدمًا على الجانبين وأعلى العريشة للتحضير لحفل زفاف. الارتفاع أقل بأربعة أقدام من العرض. أوجد ارتفاع وعرض العريشة.

30. يبلغ محيط حديقة المدينة المستطيلة 1428 قدمًا. الطول يزيد بمقدار 78 قدمًا عن ضعف العرض. ابحث عن طول وعرض المنتزه.

إجابة: الطول هو 450 قدم، العرض هو 264 قدم

حل تطبيقات الحركة الموحدة

في التمارين التالية، قم بالترجمة إلى نظام المعادلات والحل.

31. كانت شيلا ولينور يقودان سيارتهما إلى منزل جدتهما. غادرت لينور بعد ساعة واحدة من شيلا. قادت شيلا السيارة بمعدل 45 ميلاً في الساعة، وقادت لينور بمعدل 60 ميلاً في الساعة. كم من الوقت ستستغرق لينور للحاق بشيلا?

32. غادر بوب المنزل راكبًا دراجته بمعدل 10 أميال في الساعة للذهاب إلى البحيرة. غادرت شيريل، زوجته، بعد 45 دقيقة (34 ساعة)، وهي تقود سيارتها بمعدل 25 ميلاً في الساعة. كم من الوقت ستستغرق شيريل للحاق ببوب؟

إجابة: $12$ساعة

33. يمكن لماركوس قيادة قاربه 36 ميلاً أسفل النهر في ثلاث ساعات ولكنه يستغرق أربع ساعات للعودة إلى المنبع. أوجد معدل القارب في الماء الساكن ومعدل التيار.

34. يمكن لطائرة ركاب أن تطير 804 أميال في ساعتين مع رياح خلفية ولكن فقط 776 ميلاً في ساعتين في رياح عكسية. أوجد سرعة الطائرة في الهواء الساكن وسرعة الرياح.

إجابة: معدل الطائرة هو 395 ميلا في الساعة، ومعدل الرياح هو 7 ميلا في الساعة

حل تطبيقات المزيج باستخدام أنظمة المعادلات

حل تطبيقات المزيج باستخدام أنظمة المعادلات

بالنسبة للتمارين التالية، قم بالترجمة إلى نظام المعادلات والحل.

35. دفعت لين ما مجموعه 2780 دولارًا مقابل 261 تذكرة للمسرح. تبلغ تكلفة تذاكر الطلاب 10 دولارات وتذاكر البالغين 15 دولارًا. كم عدد تذاكر الطلاب وعدد تذاكر البالغين التي اشترتها لين؟

36. لدى بريام الدايمات والبنسات في حامل أكواب في سيارته. القيمة الإجمالية للعملات هي 4.21 دولارًا. يقل عدد الدايمات بثلاثة أضعاف عن أربعة أضعاف عدد البنسات. كم عدد الدايمات وعدد البنسات الموجودة في الكأس؟

إجابة: 41 سنتًا و 11 قرشًا

37. تريد Yumi صنع 12 كوبًا من مزيج الحفلات باستخدام الحلوى والمكسرات. تتطلب ميزانيتها أن يكلفها مزيج الحفلات 1.29 دولارًا للكوب. تبلغ تكلفة الحلوى 2.49 دولارًا للكوب والمكسرات 0.69 دولارًا لكل كوب. كم عدد أكواب الحلوى وكم عدد أكواب المكسرات التي يجب أن تستخدمها؟

38. يحتاج العالم إلى 70 لترًا من محلول الكحول بنسبة 40٪. يتوفر لديه حل بنسبة 30٪ و 60٪. ما عدد اللترات من الـ 30% وكم عدد اللترات من المحاليل التي تبلغ 60% التي يجب أن يخلطها لصنع محلول 40%؟

إجابة: $46\frac{2}{3}$لتر من محلول 30٪،$23\frac{1}{3}$ لتر من محلول 60٪

حل تطبيقات الاهتمام

بالنسبة للتمارين التالية، قم بالترجمة إلى نظام المعادلات والحل.

39. لدى جاك 12,000 دولار للاستثمار ويريد كسب فائدة 7.5٪ سنويًا. سيضع بعض الأموال في حساب التوفير الذي يكسب 4٪ سنويًا والباقي في حساب CD الذي يكسب 9٪ سنويًا. كم من المال يجب أن يضعه في كل حساب؟

40. عندما تتخرج من الكلية، ستدين ليندا بمبلغ 43,000 دولار في شكل قروض طلابية. سعر الفائدة على القروض الفيدرالية هو 4.5٪ ومعدل القروض المصرفية الخاصة هو 2٪. بلغ إجمالي الفائدة التي تدين بها لمدة عام واحد 1585 دولارًا. ما هو مبلغ كل قرض؟

إجابة: 29,000 دولار للقرض الفيدرالي، 14,000 دولار للقرض الخاص

حل أنظمة المعادلات ذات المتغيرات الثلاثة

حل أنظمة المعادلات ذات المتغيرات الثلاثة

في التمارين التالية، حدد ما إذا كانت الثلاثية المرتبة هي الحل للنظام.

41. $\left\{ \begin{array} {l} 3x−4y−3z=2\\2x−6y+z=3\\2x+3y−2z=3 \end{array} \right.$

ⓐ$(2,3,−1)$
ⓑ$(3,1,3)$

42. $\left\{ \begin{array} {l} y=\frac{2}{3}x−2\\x+3y−z=15\\x−3y+z=−2 \end{array} \right.$

ⓐ$(−6,5,\frac{1}{2})$
ⓑ$(5,\frac{4}{3},−3)$

إجابة: ⓐ لا ⓑ نعم

حل نظام المعادلات الخطية بثلاثة متغيرات

في التمارين التالية، قم بحل نظام المعادلات.

43. $\left\{ \begin{array} {l} 3x−5y+4z=5\\5x+2y+z=0\\2x+3y−2z=3 \end{array} \right.$

44. $\left\{ \begin{array} {l} x+\frac{5}{2}y+z=−2\\2x+2y+\frac{1}{2}z=−4\\ \frac{1}{3}x−y−z=1 \end{array} \right.$

إجابة: $(−3,2,−4)$

45. $\left\{ \begin{array} {l} 5x+3y=−6\\2y+3z=−1\\7x+z=1 \end{array} \right.$

46. $\left\{ \begin{array} {l} 2x+3y+z=12\\x+y+z=9\\3x+4y+2z=20 \end{array} \right.$

إجابة: لا يوجد حل

47. $\left\{ \begin{array} {l} −x−3y+2z=14\\−x+2y−3z=−4\\3x+y−2z=6 \end{array} \right.$

حل التطبيقات باستخدام أنظمة المعادلات الخطية ذات المتغيرات الثلاثة

48. بعد حضور إحدى مباريات البيسبول في الدوري الرئيسي، غالبًا ما يشتري المستفيدون الهدايا التذكارية. إذا اشترت الأسرة 4 قمصان وقبعة وحيوان محشو واحد، فإن المجموع هو 135 دولارًا. يشتري زوجان قميصين وقبعة و 3 حيوانات محشوة لبنات أختهم وينفقون 115 دولارًا. يشتري زوجان آخران قميصين وقبعة وحيوان محشو ويبلغ مجموعهما 85 دولارًا. ما هي تكلفة كل منتج؟

إجابة: $25, 20, 15$

حل أنظمة المعادلات باستخدام المصفوفات

اكتب المصفوفة المُعزَّزة لنظام المعادلات.

اكتب كل نظام من المعادلات الخطية في صورة مصفوفة معززة.

49. $\left\{ \begin{array} {l} 3x−y=−1\\−2x+2y=5 \end{array} \right.$

50. $\left\{ \begin{array} {l} 4x+3y=−2\\x−2y−3z=7\\2x−y+2z=−6 \end{array} \right.$

إجابة: $\left[ \begin{matrix} 4&3&0&−2\\1&−2&−3&7\\2&−1&2&−6 \end{matrix} \right]$

اكتب نظام المعادلات الذي يتوافق مع المصفوفة المعززة.

51. $\left[ \begin{array} {cc|c} 2&−4&-2\\3&−3&-1 \end{array} \right]$

52. $\left[ \begin{array} {ccc|c} 1&0&−3&-1\\1&−2&0&-2\\0&−1&2&3 \end{array} \right]$

إجابة: $\left\{ \begin{array} {l} x−3z=−1\\x−2y=−27\\−y+2z=3 \end{array} \right.$

في التمارين التالية، قم بإجراء العمليات المشار إليها على المصفوفات المعززة.

53. $\left[ \begin{array} {cc|c} 4&−6&-3\\3&2&1 \end{array} \right]$

ⓐ تبادل الصفوف 2 و 1.
ⓑ اضرب الصف 1 في 4.
ⓒ اضرب الصف 2 في 3 وأضف إلى الصف 1.

54. $\left[ \begin{array} {ccc|c} 1&−3&−2&4\\2&2&−1&-3\\4&−2&−3&-1 \end{array} \right]$

ⓐ تبادل الصفوف 2 و 3.
ⓑ اضرب الصف 1 في 2.
ⓒ اضرب الصف 3 في −2−2 وأضف إلى الصف 2.

إجابة: ⓐ$\left[ \begin{matrix} 1&−3&−2&4\\4&−2&−3&−1\\2&2&−1&−3 \end{matrix} \right]$

ⓑ$\left[ \begin{matrix} 2&−6&−4&8\\4&−2&−3&−1\\2&2&−1&−3 \end{matrix} \right]$

ⓒ$\left[ \begin{matrix} 2&−6&−4&8\\4&−2&−3&−1\\0&−6&−1&5 \end{matrix} \right]$

حل أنظمة المعادلات باستخدام المصفوفات

في التمارين التالية، قم بحل كل نظام من المعادلات باستخدام مصفوفة.

55. $\left\{ \begin{array} {l} 4x+y=6\\x−y=4 \end{array} \right.$

56. $\left\{ \begin{array} {l} 2x−y+3z=−3\\−x+2y−z=10\\x+y+z=5 \end{array} \right.$

إجابة: $(−2,5,−2)$

57. $\left\{ \begin{array} {l} 2y+3z=−1\\5x+3y=−6\\7x+z=1 \end{array} \right.$

58. $\left\{ \begin{array} {l} x+2y−3z=−1\\x−3y+z=1\\2x−y−2z=2 \end{array} \right.$

إجابة: لا يوجد حل

59. $\left\{ \begin{array} {l} x+y−3z=−1\\y−z=0\\−x+2y=1 \end{array} \right.$

حل أنظمة المعادلات باستخدام المحددات

أوجد محدِّد مصفوفة ٢ × ٢

في التمرين التالي، قم بتقييم محدد المصفوفة المربعة.

60. $\left[ \begin{matrix} 8&−4\\5&−3 \end{matrix} \right]$

إجابة: $−4$

أوجد محدِّد مصفوفة ٣ × ٣

في التمرين التالي، ابحث عن القاصرين المشار إليهم ثم قيّمهم.

61. $\left| \begin{matrix} −1&−3&2\\4&−2&−1\\−2&0&−3 \end{matrix} \right|$; ابحث عن القاصر ⓐ$a_1$ ⓑ$b_1$ ⓒ$c_2$

في التمرين التالي، قم بتقييم كل محدد من خلال التوسع بواسطة القاصرين على طول الصف الأول.

62. $\left| \begin{matrix} −2&−3&−4\\5&−6&7\\−1&2&0 \end{matrix} \right|$

إجابة: $21$في التمرين التالي، قم بتقييم كل محدد من خلال التوسع بواسطة القاصرين.

63. $\left| \begin{matrix} 3&5&4\\−1&3&0\\−2&6&1 \end{matrix} \right|$

استخدم قاعدة Cramer لحل أنظمة المعادلات

في التمارين التالية، قم بحل كل نظام من المعادلات باستخدام قاعدة كرامر

64. $\left\{ \begin{array} {l} x−3y=−9\\2x+5y=4 \end{array} \right.$

إجابة: $(−3,2)$

65. $\left\{ \begin{array} {l} 4x−3y+z=7\\2x−5y−4z=3\\3x−2y−2z=−7 \end{array} \right.$

66. $\left\{ \begin{array} {l} 2x+5y=4\\3y−z=3\\4x+3z=−3 \end{array} \right.$

إجابة: $(−3,2,3)$

67. $\left\{ \begin{array} {l} x+y−3z=−1\\y−z=0\\−x+2y=1 \end{array} \right.$

68. $\left\{ \begin{array} {l} 3x+4y−3z=−2\\2x+3y−z=−1\\2x+y−2z=6 \end{array} \right.$

إجابة: غير متناسق

حل التطبيقات باستخدام المحددات

في التمارين التالية، حدِّد ما إذا كانت النقاط المُعطاة متوازية.

69. $(0,2)$،$(−1,−1)$، و$(−2,4)$

أنظمة التمثيل البياني للمتباينات الخطية

حدِّد ما إذا كان الزوج المُرتَّب حلاً لنظام المتباينات الخطية

في التمارين التالية، حدد ما إذا كان كل زوج تم طلبه يمثل حلاً للنظام.

70. $\left\{ \begin{array} {l} 4x+y>6\\3x−y\leq 12 \end{array} \right.$

ⓐ$(2,−1)$
ⓑ$(3,−2)$

إجابة: ⓐ نعم ⓑ لا

71. $\left\{ \begin{array} {l} y>\frac{1}{3}x+2\\x−\frac{1}{4}y\leq 10 \end{array} \right.$

ⓐ$(6,5)$
ⓑ$(15,8)$

حل نظام المتباينات الخطية عن طريق التمثيل البياني

في التمارين التالية، قم بحل كل نظام بالرسم البياني.

72. $\left\{ \begin{array} {l} y<3x+1\\y\geq −x−2 \end{array} \right.$

إجابة

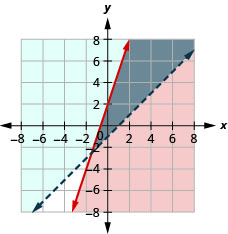
$يوضِّح الشكل الرسم البياني للمتباينات y أقل من ثلاث مرات x زائد واحد وy أكبر من أو يساوي ناقص x ناقص اثنين. يظهر خطان متقاطعان، أحدهما باللون الأحمر والآخر باللون الأزرق. تظهر المنطقة باللون الرمادي.$

الحل هو المنطقة الرمادية.

73. $\left\{ \begin{array} {l} x−y>−1\\y<\frac{1}{3}x−2 \end{array} \right.$

74. $\left\{ \begin{array} {l} 2x−3y<6\\3x+4y\geq 12 \end{array} \right.$

إجابة

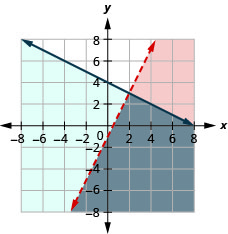
$يوضِّح الشكل التمثيل البياني للمتباينات مرتين x ناقص ثلاث مرات y أقل من ستة وثلاث مرات x زائد أربع مرات y أكبر من أو يساوي اثني عشر. يظهر خطان متقاطعان، أحدهما باللون الأحمر والآخر باللون الأزرق. تظهر المنطقة باللون الرمادي.$

الحل هو المنطقة الرمادية.

75. $\left\{ \begin{array} {l} y\leq −\frac{3}{4}x+1\\x\geq −5 \end{array} \right.$

76. $\left\{ \begin{array} {l} x+3y<5\\y\geq -\frac{1}{3}x+6 \end{array} \right.$

إجابة

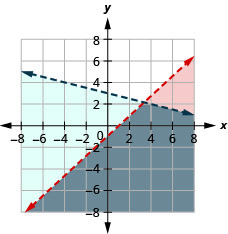
$يوضِّح الشكل التمثيل البياني للمتباينات x زائد ثلاث مرات y أقل من خمسة وy أكبر من أو يساوي ناقص ثلث x زائد ستة. يظهر خطان متوازيان، أحدهما باللون الأحمر والآخر باللون الأزرق. تظهر المنطقة باللون الرمادي.$

لا يوجد حل.

77. $\left\{ \begin{array} {l} y\geq 2x−5\\−6x+3y>−4 \end{array} \right.$

حل تطبيقات أنظمة عدم المساواة

في التمارين التالية، قم بالترجمة إلى نظام عدم المساواة وحلها.

78. تصنع روكسانا الأساور والقلائد وتبيعها في سوق المزارعين. تبيع الأساور مقابل 12 دولارًا لكل منها والقلائد مقابل 18 دولارًا لكل منها. في السوق في نهاية الأسبوع المقبل، سيكون لديها مساحة لعرض ما لا يزيد عن 40 قطعة، وتحتاج إلى بيع ما لا يقل عن 500 دولار من أجل تحقيق ربح.

ⓐ اكتب نظامًا من عدم المساواة لنمذجة هذا الموقف.
ⓑ رسم بياني للنظام.
ⓒ هل يجب أن تعرض 26 سوارًا و 14 قلادًا؟
ⓓ هل يجب أن تعرض 39 سوارًا وقلادة واحدة؟

إجابة

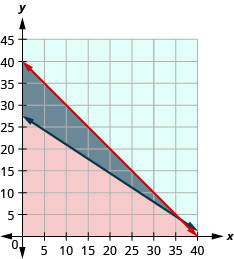
ⓐ$\left\{ \begin{array} {l} b\geq 0\\ n\geq 0\\ b+n\leq 40\\12b+18n\geq 500 \end{array} \right.$
ⓑ

$يوضِّح الشكل التمثيل البياني لـ b زائد n يساوي أربعين واثني عشر ب زائد ثمانية عشر نيوتن يساوي خمسمائة. يظهر خطان متقاطعان، أحدهما باللون الأحمر والآخر باللون الأزرق. تظهر المنطقة باللون الرمادي.$

ⓒ نعم
ⓓ لا

79. لدى آني ميزانية قدرها 600 دولار لشراء الكتب ذات الغلاف الورقي والكتب ذات الغلاف المقوى لفصلها الدراسي. إنها تريد أن يزيد عدد الكتب ذات الغلاف المقوى بخمسة أضعاف على الأقل عن ثلاثة أضعاف عدد الكتب ذات الغلاف الورقي. تبلغ تكلفة الكتب ذات الغلاف الورقي 4 دولارات لكل منها وتكلفة الكتب ذات الغلاف المقوى 15 دولارًا لكل منها.

ⓐ اكتب نظامًا من عدم المساواة لنمذجة هذا الموقف.
ⓑ رسم بياني للنظام.
ⓒ هل يمكنها شراء 8 كتب ورقية و40 كتابًا بغلاف مقوى؟
ⓓ هل يمكنها شراء 10 كتب ورقية و37 كتابًا بغلاف مقوى؟

اختبار ممارسة الفصل

في التمارين التالية، قم بحل الأنظمة التالية بالرسم البياني.

1. $\left\{ \begin{array} {l} x−y=5\\x+2y=−4 \end{array} \right.$

إجابة

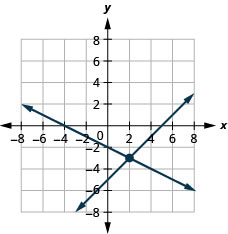
$يوضِّح الشكل التمثيل البياني للمتباينات h يساوي ثلاثة p زائد خمسة وأربعة في p زائد خمسة عشر في h يساوي ستمائة. يظهر خطان متقاطعان، أحدهما باللون الأحمر والآخر باللون الأزرق. تظهر المنطقة باللون الرمادي.$

$(2,−3)$

2. $\left\{ \begin{array} {l} x−y>−2\\y\leq 3x+1 \end{array} \right.$

في التمارين التالية، قم بحل كل نظام من المعادلات. استخدم إما الاستبدال أو الإزالة.

3. $\left\{ \begin{array} {l} x+4y=6\\−2x+y=−3 \end{array} \right.$

إجابة: $(2,1)$

4. $\left\{ \begin{array} {l} −3x+4y=2\\5x−5y=−23 \end{array} \right.$

5. $\left\{ \begin{array} {l} x+y−z=−1\\2x−y+2z=8\\−3x+2y+z=−9 \end{array} \right.$

إجابة: $(2,−2,1)$

حل نظام المعادلات باستخدام مصفوفة.

6. $\left\{ \begin{array} {l} 2x+y=7\\x−2y=6 \end{array} \right.$

7. $\left\{ \begin{array} {l} −3x+y+z=−4\\−x+2y−2z=1\\2x−y−z=−1 \end{array} \right.$

إجابة: $(5,7,4)$

حل باستخدام قاعدة كرامر.

8. $\left\{ \begin{array} {l} 3x+y=−3\\2x+3y=6 \end{array} \right.$

9. قم بتقييم المحدد من خلال التوسع من قبل القاصرين:

$\left| \begin{matrix} 3&−2&−2\\2&−1&4\\−1&0&−3 \end{matrix} \right|$

إجابة: $99$

في التمارين التالية، قم بالترجمة إلى نظام المعادلات والحل.

10. يقوم جريج بالتجديف في قاربه عند المنبع، مقابل التيار، إلى بقعة صيد على بعد 10 أميال. إذا قام بالتجديف في اتجاه مجرى النهر لمدة 2.5 ساعة واستغرقت رحلة العودة 1.25 ساعة، فأوجد سرعة التيار وسرعة التجديف في الماء الساكن.

11. يحتاج الصيدلي إلى 20 لترًا من محلول ملحي بنسبة 2٪. يتوفر لديه حل بنسبة 1٪ و 5٪. ما عدد اللترات من المحاليل البالغة 1% وعدد اللترات من المحاليل البالغة 5% التي ينبغي عليها خلطها لصنع محلول 2%؟

إجابة: 15 لترًا من محلول 1٪، 5 لترات من محلول 5٪

12. استثمر أرنولد 64,000 دولار، بعضها بفائدة 5.5٪ والباقي بنسبة 9٪. كم استثمر بكل معدل إذا حصل على 4500 دولار كفائدة في عام واحد؟

13. تبيع مجموعة شباب الكنيسة الوجبات الخفيفة لجمع الأموال لحضور مؤتمرهم. باعت إيمي رطلين من الحلوى و 3 علب من البسكويت وعلبة واحدة من الفشار بإجمالي مبيعات 65 دولارًا. باع بريان 4 أرطال من الحلوى و 6 علب من البسكويت و 3 علب من الفشار بإجمالي مبيعات 140 دولارًا. باعت بولينا 8 أرطال من الحلوى و 8 علب من البسكويت و 5 علب من الفشار بإجمالي مبيعات 250 دولارًا. ما هي تكلفة كل منتج؟

إجابة: تكلفة الحلوى 20 دولارًا؛ وتكلفة البسكويت 5 دولارات؛ وتكلفة الفشار 10 دولارات.

14. تنفق الشركة المصنعة لقضيب الجرانولا 1.20 دولارًا لصنع كل بار وبيعها مقابل 2 دولار. لدى الشركة المصنعة أيضًا تكاليف ثابتة كل شهر قدرها 8000 دولار.

ⓐ ابحث عن وظيفة التكلفة C عند تصنيع قضبان الجرانولا x
ⓑ ابحث عن وظيفة الإيرادات R عند بيع قضبان الجرانولا x.
ⓒ اعرض نقطة التعادل من خلال رسم بياني لكل من وظائف الإيرادات والتكلفة على نفس الشبكة.
ⓓ ابحث عن نقطة التعادل. فسر ما تعنيه نقطة التعادل.

15. ترجم إلى نظام عدم المساواة وقم بحله.

تريد آندي ألا تنفق أكثر من 50 دولارًا على هدايا الهالوين. تريد شراء قطع حلوى تكلف الواحدة منها دولارًا واحدًا ومصاصات تكلف 0.50 دولارًا لكل منها، وتريد أن يكون عدد المصاصات ثلاثة أضعاف عدد قطع الحلوى على الأقل.

إجابة

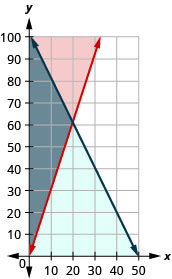
ⓐ$\left\{ \begin{array} {l} C\geq 0\\ L\geq 0\\ C+0.5L\leq 50 \\ L\geq 3C \end{array} \right.$
ⓑ

$يوضِّح الشكل الرسم البياني لمعادلتين. يظهر خطان متقاطعان، أحدهما باللون الأحمر والآخر باللون الأزرق. يمر الخط الأحمر عبر الأصل. تظهر المنطقة باللون الرمادي.$

ⓒ لا
ⓓ نعم