4.7: حل أنظمة المعادلات باستخدام المحددات

Last updated
Save as PDF

Page ID: 201468

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

أوجد محدِّد مصفوفة 2×2
أوجد محدِّد مصفوفة ٣×٣
استخدم قاعدة Cramer لحل أنظمة المعادلات
حل التطبيقات باستخدام المحددات

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

قم بالتبسيط:$5(−2)−(−4)(1)$.
إذا فاتتك هذه المشكلة، راجع [link].
قم بالتبسيط:$−3(8−10)+(−2)(6−3)−4(−3−(−4))$.
إذا فاتتك هذه المشكلة، راجع [link].
قم بالتبسيط:$\frac{−12}{−8}$.
إذا فاتتك هذه المشكلة، راجع [link].

في هذا القسم سوف نتعلم طريقة أخرى لحل أنظمة المعادلات الخطية تسمى قاعدة كرامر. قبل أن نتمكن من البدء في استخدام القاعدة، نحتاج إلى تعلم بعض التعريفات والرموز الجديدة.

إيجاد قيمة محدد$2×2$ المصفوفة

إذا كانت المصفوفة تحتوي على نفس عدد الصفوف والأعمدة، فإننا نسميها مصفوفة مربعة. تحتوي كل مصفوفة مربعة على رقم حقيقي مرتبط بها يسمى المحدد لها. للعثور على محدد المصفوفة المربعة$\left[ \begin{matrix} a &b \\ c&d \end{matrix} \right] $، نكتبها أولاً كـ$\left| \begin{matrix} a &b \\ c&d \end{matrix} \right| $. للحصول على قيمة الرقم الحقيقي للمُحدد، نطرح منتجات الأقطار، كما هو موضح.

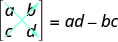
$يتم عرض محدد 2 × 2، مع كون الصف الأول هو a و b والثاني هو c، d. تتم كتابة هذه القيم بين سطرين رأسيين بدلاً من الأقواس كما في حالة المصفوفات. يظهر سهمان، أحدهما من a إلى d، والآخر من c إلى b، وهذا المحدد يساوي ad ناقص bc.$

محدد

محدد أي مصفوفة مربعة$\left[ \begin{matrix} a &b \\ c&d \end{matrix} \right] $، حيث تكون a و b و c و d أرقامًا حقيقية، هو

\[\left| \begin{matrix} a &b \\ c&d \end{matrix} \right| =ad−bc \nonumber \]

مثال$\PageIndex{1}$

قم بتقييم محدد ⓐ$\left[ \begin{matrix} 4 &-2 \\ 3&-1 \end{matrix} \right] $ ⓑ$\left[ \begin{matrix} -3 &-4 \\ -2&0 \end{matrix} \right] $.

إجابة

ⓐ

	$.$
اكتب المحدد.	$.$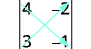
اطرح منتجات الأقطار.	$.$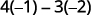
قم بالتبسيط.	$.$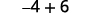
قم بالتبسيط.	$.$

ⓑ

	$.$
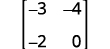
اكتب المحدد.	$.$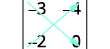
اطرح منتجات الأقطار.	$.$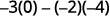
قم بالتبسيط.	$.$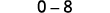
قم بالتبسيط.	$.$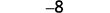

مثال$\PageIndex{2}$

قم بتقييم محدد ⓐ$\left[ \begin{matrix} 5&−3\\2&−4 \end{matrix} \right] $ ⓑ$\left[ \begin{matrix} −4&−6\\0&7 \end{matrix} \right] $.

إجابة: ⓐ$−14$؛ ⓑ$−28$

مثال$\PageIndex{3}$

قم بتقييم محدد ⓐ$\left[ \begin{matrix} −1&3\\−2&4 \end{matrix} \right] $ ⓑ$\left[ \begin{matrix} −7&−3\\−5&0 \end{matrix} \right] $.

إجابة: ⓐ 2 ⓑ$−15$

إيجاد قيمة محدد$3×3$ المصفوفة

لتقييم محدد$3×3$ المصفوفة، يجب أن نكون قادرين على تقييم ثانوي الإدخال في المحدد. والصغير في الإدخال هو$2×2$ المحدد الذي يتم العثور عليه من خلال حذف الصف والعمود في$3×3$ المحدد الذي يحتوي على الإدخال.

قاصر عند الدخول$3×3$ A DETERMINANT

والصغير في الإدخال في$3×3$ المحدد هو$2×2$ المحدد الذي يتم العثور عليه من خلال حذف الصف والعمود في$3×3$ المحدد الذي يحتوي على الإدخال.

للعثور على عنصر الإدخال الثانوي$a_1$، نزيل الصف والعمود اللذين يحتويان عليه. لذلك نزيل الصف الأول والعمود الأول. ثم نكتب$2×2$ المحدد الذي يبقى.

$الصف الأول من محدد 3 × 3 هو a1، b1، c1. الصف 2 هو a2، b2، c2. الصف 3 هو a3، b3، c3. تم تمييز a1. تطرد الخطوط الصف الأول والعمود الأول. ما تبقى يسمى ثانوي من a1. يظهر كمحدد منفصل يكون صفه الأول b2 و c2 والصف الثاني هو b3 و c3.$

للعثور على الإدخال الثانوي$b_2$، نزيل الصف والعمود اللذين يحتويان عليه. لذلك نزيل$2^{nd}$ الصف$2^{nd}$ والعمود. ثم نكتب$2×2$ المحدد الذي يبقى.

$الصف الأول من محدد 3 × 3 هو a1، b1، c1. الصف 2 هو a2، b2، c2. الصف 3 هو a3، b3، c3. تم تمييز b2. تطرد الخطوط الصف الثاني والعمود الثاني. ما تبقى هو جزء صغير من b2. يتم كتابته كمحدد منفصل يكون صفه الأول هو a1 و c1 والصف الثاني هو a3 و c3.$

مثال$\PageIndex{4}$

بالنسبة للمحدد$\left| \begin{matrix} 4&−2&3\\1&0&−3\\−2&−4&2 \end{matrix} \right|$، ابحث عن الصغير لـ ⓐ$a_1$ ⓑ$b_3$ ⓒ ثم قيّمه$c_2$.

إجابة

ⓐ

	$.$
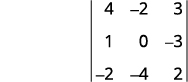
قم بإزالة الصف والعمود الذي يحتوي على$a_1$.	$.$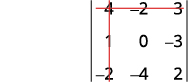
اكتب$2×2$ المحدد المتبقي.	$.$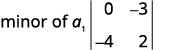
تقييم.	$.$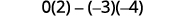
قم بالتبسيط.	$.$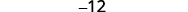

ⓑ

قم بإزالة الصف والعمود الذي يحتوي على$b_3$.	$.$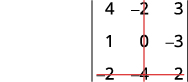
اكتب$2×2$ المحدد المتبقي.	$.$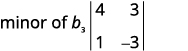
تقييم.	$.$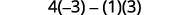
قم بالتبسيط.	$.$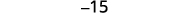

ⓒ

	$.$
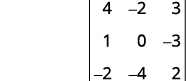
قم بإزالة الصف والعمود الذي يحتوي على$c_2$.	$.$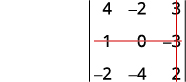
اكتب$2×2$ المحدد المتبقي.	$.$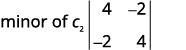
تقييم.	$.$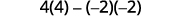
قم بالتبسيط.	$.$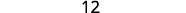

مثال$\PageIndex{5}$

بالنسبة للمحدد$\left| \begin{matrix} 1&−1&4\\0&2&−1\\−2&−3&3 \end{matrix} \right|$، ابحث عن الصغير لـ ⓐ$a_1$ ⓑ$b_2$ ⓒ ثم قيّمه$c_3$.

إجابة: ⓐ 3 ⓑ 11 ⓒ 2

مثال$\PageIndex{6}$

بالنسبة للمحدد$\left| \begin{matrix} −2&−1&0\\3&0&−1\\−1&−2&3 \end{matrix} \right|$، ابحث عن الصغير لـ ⓐ$a_2$ ⓑ$b_3$ ⓒ ثم قيّمه$c_2$.

إجابة: ⓐ$−3$ ⓑ 2 ⓒ 3

نحن الآن على استعداد لتقييم$3×3$ المحدد. للقيام بذلك، نقوم بالتوسع ليشمل القاصرين، مما يسمح لنا بتقييم$3×3$ المحددات باستخدام$2×2$ المحددات - التي نعرف بالفعل كيفية تقييمها!

لتقييم$3×3$ المحدد من خلال التوسع بواسطة القاصرين على طول الصف الأول، نستخدم النمط التالي:

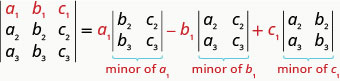
$محدد 3 × 3 يساوي a1 مضروبًا في الحد الأدنى من a1 ناقص b1 مضروبًا في b1 زائد c1 مضروبًا في c1.$

تذكر أنه للعثور على ثانوي الإدخال، نزيل الصف والعمود الذي يحتوي على الإدخال.

التوسع من قبل القاصرين على طول الصف الأول لتقييم$3×3$ DETERMINANT

لتقييم$3×3$ المحدد من خلال التوسع بواسطة القاصرين على طول الصف الأول، اتبع النمط التالي:

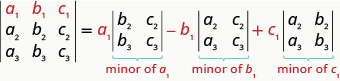
$محدد 3 × 3 يساوي a1 مضروبًا في الحد الأدنى من a1 ناقص b1 مضروبًا في b1 زائد c1 مضروبًا في c1.$

مثال$\PageIndex{7}$

قم بتقييم المحدد$\left| \begin{matrix} 2&−3&−1\\3&2&0\\−1&−1&−2 \end{matrix} \right|$ من خلال التوسع بواسطة القاصرين على طول الصف الأول.

إجابة

	$.$
قم بالتوسع من قبل القاصرين على طول الصف الأول	$.$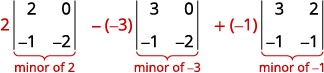
قم بتقييم كل محدد.	$.$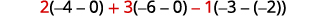
قم بالتبسيط.	$.$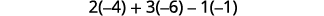
قم بالتبسيط.	$.$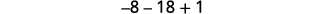
قم بالتبسيط.	$.$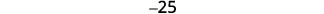

مثال$\PageIndex{8}$

قم بتقييم المحدد$\left| \begin{matrix} 3&−2&4\\0&−1&−2\\2&3&−1 \end{matrix} \right|$، من خلال التوسع بواسطة القاصرين على طول الصف الأول.

إجابة: 37

مثال$\PageIndex{9}$

قم بتقييم المحدد$\left| \begin{matrix} 3&−2&−2\\2&−1&4\\−1&0&−3 \end{matrix} \right|$، من خلال التوسع بواسطة القاصرين على طول الصف الأول.

إجابة: 7

لتقييم أحد$3×3$ المحددات، يمكننا التوسع بواسطة القاصرين باستخدام أي صف أو عمود. يؤدي اختيار صف أو عمود آخر غير الصف الأول أحيانًا إلى تسهيل العمل.

عندما نتوسع بأي صف أو عمود، يجب أن نكون حذرين بشأن علامة الشروط في التوسيع. لتحديد علامة المصطلحات، نستخدم مخطط نمط الإشارة التالي.

\[\left| \begin{matrix} +&−&+\\−&+&−\\+&−&+ \end{matrix} \right|\nonumber\]

نمط التوقيع

عند التوسيع بواسطة القاصرين باستخدام صف أو عمود، تتبع علامة المصطلحات في التوسيع النمط التالي. \[\left| \begin{matrix} +&−&+\\−&+&−\\+&−&+ \end{matrix} \right|\nonumber\]

لاحظ أن نمط العلامة في الصف الأول يطابق العلامات بين الشروط في التوسيع بالصف الأول.

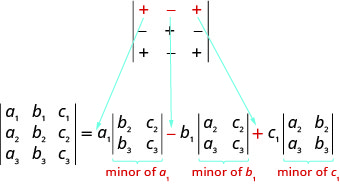
$يحتوي محدد 3 × 3 على الصف 1: زائد، ناقص، زائد، صف 2: ناقص، زائد، ناقص، صف 3: زائد، ناقص، زائد. تشير كل علامة من العلامات الثلاث في الصف الأول إلى محدد بسيط في توسيع محدد 3 × 3. بالإضافة إلى النقاط الصغرى من a1، ناقص إلى القاصر b1 والإضافة إلى القاصر c1.$

نظرًا لأنه يمكننا التوسيع بأي صف أو عمود، كيف نحدد الصف أو العمود الذي يجب استخدامه؟ عادةً ما نحاول اختيار صف أو عمود يجعل الحساب أسهل. إذا كان المحدد يحتوي على 0، فإن استخدام الصف أو العمود الذي يحتوي على 0 سيجعل العمليات الحسابية أسهل.

مثال$\PageIndex{10}$

قم بتقييم المحدد$\left| \begin{matrix} 4&−1&−3\\3&0&2\\5&−4&−3 \end{matrix} \right|$ من خلال التوسع من قبل القاصرين.

إجابة

للتوسع من قبل القاصرين، نبحث عن صف أو عمود يجعل حساباتنا أسهل. نظرًا لوجود 0 في الصف الثاني والعمود الثاني، فإن التوسع بأي منهما يعد اختيارًا جيدًا. نظرًا لأن الصف الثاني يحتوي على عدد أقل من السلبيات من العمود الثاني، فسنقوم بالتوسع في الصف الثاني.

	$.$
قم بالتوسيع باستخدام الصف الثاني.
احذر من العلامات.	$.$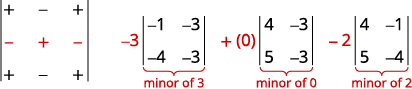
قم بتقييم كل محدد.	$.$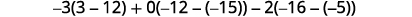
قم بالتبسيط.	$.$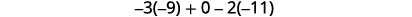
قم بالتبسيط.	$.$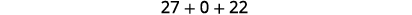
أضف.	$.$

مثال$\PageIndex{11}$

قم بتقييم المحدد$\left| \begin{matrix} 2&−1&−3\\0&3&−4\\3&−4&−3 \end{matrix} \right|$ من خلال التوسع من قبل القاصرين.

إجابة: $−11$

مثال$\PageIndex{12}$

قم بتقييم المحدد$\left| \begin{matrix} −2&−1&−3\\−1&2&2\\4&−4&0 \end{matrix} \right|$ من خلال التوسع من قبل القاصرين.

إجابة: 8

استخدم قاعدة Cramer لحل أنظمة المعادلات

قاعدة كرامر هي طريقة لحل أنظمة المعادلات باستخدام المحددات. يمكن اشتقاقه من خلال حل الشكل العام لأنظمة المعادلات عن طريق الحذف. سنوضح هنا قاعدة كلا النظامين لمعادلتين بمتغيرين وللأنظمة المكونة من ثلاث معادلات ذات ثلاثة متغيرات.

لنبدأ بأنظمة معادلتين بمتغيرين.

قاعدة كرامر لحل نظام من معادلتين

بالنسبة لنظام المعادلات$\left\{\begin{array} {l} a_1x+b_1y=k_1 \\ a_2x+b_2y=k_2\end{array}\right.$،$(x,y)$ يمكن تحديد الحل من خلال

$x هو Dx عند D و y هو Dy on D حيث D هو المحدد بالصف 1: a1، b1 والصف 2 a2، b2، استخدم معاملات المتغيرات؛ Dx هو المحدد بالصف 1: k1، b1 والصف 2: k2، b2، استبدل المعاملات x بالحروف الساكنة؛ Dy هو المحدد بالصف 1: a1، k1 والصف 2: a2، k2، استبدل y معاملات مع الثوابت$

لاحظ أنه لتشكيل المحدد D، نستخدم معاملات المتغيرات.

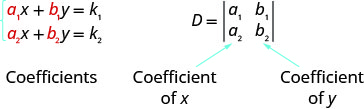
$المعادلات هي a1x زائد b1y يساوي k1 و a2x بالإضافة إلى b2y يساوي k2. هنا، a1، a2، b1، b2 هي معاملات. المحدد هو D مع الصف 1: a1 و b1 والصف 2: a2، b2. يحتوي العمود 1 على معاملات x والعمود 2 له معاملات$

لاحظ أنه لتشكيل المحدد$D_x$$D_y$ ونستبدل الثوابت بمعاملات المتغير الذي نجده.

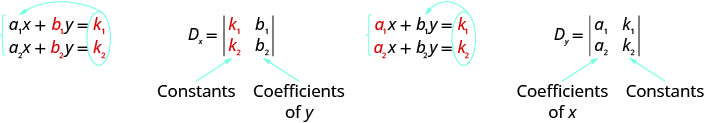
$المعادلات هي a1x زائد b1y يساوي k1 و a2x بالإضافة إلى b2y يساوي k2. هنا، a1، a2، b1، b2 هي معاملات. المحدد هو أن Dx يحتوي على الصف 1: k1 و b1 والصف 2: k2، b2. هنا العمودان 1 و 2 هما ثوابت ومعاملات y على التوالي. يحتوي يوم المحدد على الصف 1: a1 و k1 والصف 2: a2 و k2. هنا، يمثل العمودان 1 و 2 معاملات x والثوابت على التوالي.$

مثال$\PageIndex{13}$: How to Solve a System of Equations Using Cramer’s Rule

حل المشكلة باستخدام قاعدة كرامر:$\left\{ \begin{array} {l} 2x+y=−4\\3x−2y=−6\end{array}\right.$

إجابة: $المعادلات هي 2x زائد y يساوي ناقص 4 و 3x ناقص 2y يساوي ناقص 6. الخطوة 1. قم بتقييم المحدد D باستخدام معاملات المتغيرات. يحتوي المحدد D على الصف 1:2، 1 والصف 2:3، ناقص 2. إذن، D هو ناقص 7.$ $الخطوة 2. قم بتقييم المحدد Dx. استخدم الثوابت بدلاً من معاملات x. نستبدل معاملات x و 2 و 3 بالثوابت والسالب 4 والسالب 6. نحصل على Dx يساوي 14.$ $الخطوة 3. قم بتقييم اليوم المحدد. استخدم الثوابت بدلاً من معاملات y. نستبدل معاملات y و 1 و 2 بالثوابت والسالب 4 والسالب 6. نحصل على يوم يساوي 0.$ $الخطوة 4. ابحث عن x و y. باستبدال قيم D و Dx و Dy في المعادلات x التي تساوي Dx عند D و y تساوي Dy عند D، نحصل على x يساوي ناقص 2 و y يساوي 0.$ $الخطوة 5. اكتب الحل في صورة زوج مرتب ناقص 2، 0.$ $الخطوة 6. تأكد من أن الزوج المطلوب هو حل لكل من المعادلتين الأصليتين.$

مثال$\PageIndex{14}$

حل المشكلة باستخدام قاعدة كرامر:$\left\{\begin{array} {l} 3x+y=−3 \\ 2x+3y=6 \end{array} \right.$

إجابة: $(−\frac{15}{7},\frac{24}{7})$

مثال$\PageIndex{15}$

حل المشكلة باستخدام قاعدة كرامر:$\left\{\begin{array} {l} −x+y=2\\2x+y=−4 \end{array} \right.$

إجابة: $(−2,0)$

حل نظامًا من معادلتين باستخدام قاعدة CRAMER.

قم بتقييم المحدد D باستخدام معاملات المتغيرات.
قم بتقييم المحدد$D_x$. استخدم الثوابت بدلاً من معاملات x.
قم بتقييم المحدد$D_y$. استخدم الثوابت بدلاً من معاملات y.
ابحث عن x و y. $x=\frac{D_x}{D}$،$y=\frac{D_y}{D}$
اكتب الحل كزوج مطلوب.
تأكد من أن الزوج المطلوب هو حل لكل من المعادلتين الأصليتين.

لحل نظام من ثلاث معادلات بثلاثة متغيرات باستخدام قاعدة كرامر، نقوم بشكل أساسي بما فعلناه لنظام من معادلتين. ومع ذلك، يتعين علينا الآن حل ثلاثة متغيرات للحصول على الحل. ستكون المحددات أيضًا هي$3×3$ التي ستجعل عملنا أكثر إثارة للاهتمام!

قاعدة كرامر لحل نظام من ثلاث معادلات

بالنسبة لنظام المعادلات$\left\{\begin{array} {l} a_1x+b_1y+c_1z=k_1\\a_2x+b_2y+c_2z=k_2\\a_3x+b_3y+c_3z=k_3\end{array}\right.$،$(x,y,z)$ يمكن تحديد الحل من خلال

$x هو Dx عند D، y هو Dy on D و z هو Dz على D، حيث D هو المحدد مع الصف 1: a1، b1، c1، الصف 2: a2، b2، c2، الصف 3: a3، b3، c3، استخدم معاملات المتغيرات؛ Dx هو المحدد مع الصف 1: k1، b1، c1، الصف 2: k2، b2، c2 والصف 3: k3، b3، c3، استبدل معاملات x مع الحروف الساكنة؛ Dy هي المحدد مع الصف 1: a1، k1، c1، الصف 2: a2، k2، c2 والصف 3: a3، k3، c3، استبدل معاملات y بالثوابت؛ Dz هو المحدد بالصف 1: a1، b1، k1؛ الصف 2: a2، b2، k2، الصف 3: a3، b3، k3؛ استبدل معاملات z بالثوابت.$

مثال$\PageIndex{16}$

حل نظام المعادلات باستخدام قاعدة كرامر:$\left\{\begin{array} {l} 3x−5y+4z=5\\5x+2y+z=0\\2x+3y−2z=3 \end{array} \right.$

إجابة

قم بتقييم المحدد D.	$.$
قم بالتوسيع بواسطة القاصرين باستخدام العمود 1.
$.$	$.$
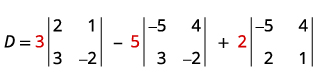
قم بتقييم المحددات.	$.$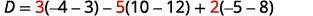
قم بالتبسيط.	$.$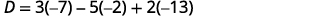
قم بالتبسيط.	$.$
قم بالتبسيط.	$.$
قم بتقييم المحدد$D_x$. استخدم الثوابت لاستبدال معاملات x.	$.$
قم بالتوسيع بواسطة القاصرين باستخدام العمود 1.	$.$
قم بتقييم المحددات.	$.$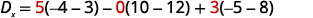
قم بالتبسيط.	$.$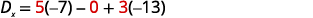
قم بالتبسيط.	$.$
قم بتقييم المحدد Dy.Dy. استخدم الثوابت لاستبدال معاملات y.	$.$
$.$	$.$
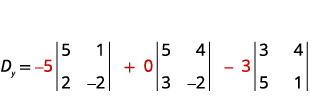
قم بتقييم المحددات.	$.$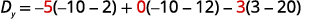
قم بالتبسيط.	$.$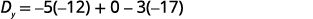
قم بالتبسيط.	$.$
قم بالتبسيط.	$.$
قم بتقييم المحدد Dz.Dz. استخدم الثوابت لاستبدال معاملات z.	$.$
$.$	$.$
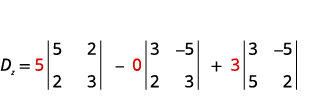
قم بتقييم المحددات.	$.$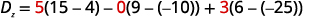
قم بالتبسيط.	$.$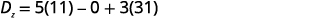
قم بالتبسيط.	$.$
قم بالتبسيط.	$.$
ابحث عن x و y و z.	$.$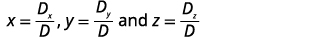
استبدل القيم.	$.$
قم بالتبسيط.	$.$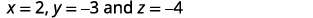
اكتب الحل في صورة ثلاثية مرتبة.	$.$
تأكد من أن الثلاثية المرتبة هي الحل لجميع المعادلات الأصلية الثلاث.	نترك الشيك لك.
	الحل هو$(2,−3,−4)$.

مثال$\PageIndex{17}$

حل نظام المعادلات باستخدام قاعدة كرامر:$\left\{\begin{array} {l} 3x+8y+2z=−5\\2x+5y−3z=0\\x+2y−2z=−1 \end{array} \right.$

إجابة: $(−9,3,−1)$

مثال$\PageIndex{18}$

حل نظام المعادلات باستخدام قاعدة كرامر:$\left\{\begin{array} {l} 3x+y−6z=−3\\2x+6y+3z=0\\3x+2y−3z=−6 \end{array} \right.$

إجابة: $(−6,3,−2)$

لا تعمل قاعدة كرامر عندما تكون قيمة محدد D هي 0، لأن هذا يعني أننا سنقسم على 0. ولكن عندما يكون$D=0$ النظام إما غير متناسق أو معتمدًا.

عندما تكون قيمة and$D=0$$D_x,\space D_y$ و D كلها صفرية، يكون النظام ثابتًا ومعتمدًا وهناك العديد من الحلول بلا حدود.

عندما تكون قيمة$D=0$$D_x,\space D_y$ و وليست$D_z$ كلها صفرية، يكون النظام غير متناسق ولا يوجد حل.

أنظمة المعادلات التابعة وغير المتسقة

بالنسبة لأي نظام من المعادلات، حيث قيمة المحدد$D=0$،

\[ \begin{array} {lll} \textbf{Value of determinants} &\textbf{Type of system} &\textbf{Solution} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are all zero}} &\text{consistent and dependent} &\text{infinitely many solutions} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are not all zero}} &\text{inconsistent} &\text{no solution} \end{array} \nonumber\]

في المثال التالي، سنستخدم قيم المحددات للعثور على حل النظام.

مثال$\PageIndex{19}$

حل نظام المعادلات باستخدام قاعدة كرامر:$\left\{\begin{array} {l} x+3y=4\\−2x−6y=3 \end{array} \right.$

إجابة

$\begin{array} {ll} {} &{\left\{\begin{array} {l} x+3y=4\\−2x−6y=3 \end{array} \right.} \\ {\begin{array} {l} \text{Evaluate the determinantD,using the} \\ \text{coefficients of the variables.} \end{array}} &{D=\left|\begin{matrix} 1&3\\−2&−6\end{matrix}\right|} \\ {} &{D=−6−(−6)} \\ {} &{D=0} \end{array} $

لا يمكننا استخدام قاعدة Cramer لحل هذا النظام. ولكن بالنظر إلى قيمة المحددات$D_x$$D_y$، يمكننا تحديد ما إذا كان النظام تابعًا أم غير متسق.

$\begin{array} {ll} {\text{Evaluate the determinant }D_x.} &{D_x=\left|\begin{matrix} 4&3\\3&−6\end{matrix}\right|} \\ {} &{D_x=−24−9} \\ {} &{D_x=15} \end{array} $

نظرًا لأن جميع المحددات ليست صفرية، فإن النظام غير متسق. لا يوجد حل.

مثال$\PageIndex{20}$

حل نظام المعادلات باستخدام قاعدة كرامر:$\left\{\begin{array} {l} 4x−3y=8\\8x−6y=14 \end{array} \right.$

إجابة: لا يوجد حل

مثال$\PageIndex{21}$

حل نظام المعادلات باستخدام قاعدة كرامر:$\left\{\begin{array} {l} x=−3y+4\\2x+6y=8 \end{array} \right.$

إجابة: حلول لانهائية

حل التطبيقات باستخدام المحددات

يسمح لنا تطبيق مثير للمحددات باختبار ما إذا كانت النقاط متوازية. ثلاث نقاط$(x_1,y_1)$،$(x_2,y_2)$$(x_3,y_3)$ وتكون متوازية إذا كان المحدد أدناه صفرًا فقط.

\[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]

اختبار النقاط المستقيمة

ثلاث نقاط$(x_1,y_1)$،$(x_2,y_2)$$(x_3,y_3)$ وتكون متوازية إذا وفقط إذا

\[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]

سنستخدم هذه الخاصية في المثال التالي.

مثال$\PageIndex{22}$

حدِّد ما إذا كانت النِّقاط$(5,−5)$$(4,−3)$،$(3,−1)$ والنقاط، و

إجابة

	$.$
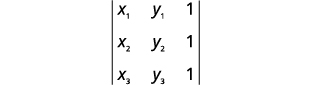
استبدل القيم بالمحدد. $(5,−5)$،$(4,−3)$، و$(3,−1)$	$.$
قم بتقييم المحدد من خلال التوسع بواسطة القاصرين باستخدام العمود 3.	$.$
قم بتقييم المحددات.	$.$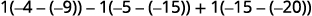
قم بالتبسيط.	$.$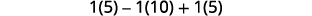
قم بالتبسيط.	$.$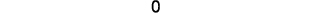
	قيمة المحدد هي 0، وبالتالي فإن النقاط متوازية.

مثال$\PageIndex{23}$

حدِّد ما إذا كانت النِّقاط$(3,−2)$$(5,−3)$،$(1,−1)$ والنقاط، و

إجابة: نعم

مثال$\PageIndex{24}$

حدِّد ما إذا كانت النِّقاط$(−4,−1)$$(−6,2)$،$(−2,−4)$ والنقاط، و

إجابة: نعم

يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية في حل أنظمة عدم المساواة الخطية عن طريق الرسوم البيانية.

حل أنظمة المتباينات الخطية عن طريق التمثيل البياني
أنظمة المتباينات الخطية

المفاهيم الرئيسية

المحدد: محدد أي مصفوفة مربعة$\left[\begin{matrix}a&b\\c&d\end{matrix}\right]$، حيث تكون a و b و c و d أرقامًا حقيقية، هو
\[\left|\begin{matrix}a&b\\c&d\end{matrix}\right|=ad−bc\nonumber\]
التوسيع بواسطة القاصرين على طول الصف الأول لتقييم محدد 3 × 3: لتقييم$3×3$ المحدد عن طريق التوسع بواسطة القاصرين على طول الصف الأول، النمط التالي:
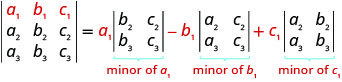
$محدد 3 × 3 يساوي a1 مضروبًا في الحد الأدنى من a1 ناقص b1 مضروبًا في b1 زائد c1 مضروبًا في c1.$
نمط الإشارة: عند التوسيع بواسطة القاصرين باستخدام صف أو عمود، تتبع علامة المصطلحات في التوسيع النمط التالي.
\[\left|\begin{matrix}+&−&+\\−&+&−\\+&−&+\end{matrix}\right|\nonumber\]
قاعدة كرامر: بالنسبة لنظام المعادلات$\left\{\begin{array} {l} a_1x+b_1y=k_1\\a_2x+b_2y=k_2\end{array}\right.$،$(x,y)$ يمكن تحديد الحل من خلال
$x هو Dx عند D و y هو Dy on D حيث D هو المحدد بالصف 1: a1، b1 والصف 2 a2، b2، استخدم معاملات المتغيرات؛ Dx هو المحدد بالصف 1: k1، b1 والصف 2: k2، b2، استبدل المعاملات x بالحروف الساكنة؛ Dy هو المحدد بالصف 1: a1، k1 والصف 2: a2، k2، استبدل y معاملات مع الثوابت.$
ملاحظة أنه لتشكيل المحدد D، نستخدم أخذ معاملات المتغيرات.
كيفية حل نظام من معادلتين باستخدام قاعدة كرامر.
1. قم بتقييم المحدد D باستخدام معاملات المتغيرات.
2. قم بتقييم المحدد$D_x$. استخدم الثوابت بدلاً من معاملات x.
3. قم بتقييم المحدد$D_y$. استخدم الثوابت بدلاً من معاملات y.
4. ابحث عن x و y. $x=\frac{D_x}{D}$،$y=\frac{D_y}{D}$.
5. اكتب الحل كزوج مطلوب.
6. تأكد من أن الزوج المطلوب هو حل لكل من المعادلتين الأصليتين.
7. أنظمة المعادلات التابعة وغير المتسقة: لأي نظام من المعادلات، حيث قيمة المحدد$D=0$،\[ \begin{array} {lll} \textbf{Value of determinants} &\textbf{Type of system} &\textbf{Solution} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are all zero}} &\text{consistent and dependent} &\text{infinitely many solutions} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are not all zero}} &\text{inconsistent} &\text{no solution} \end{array} \nonumber\]
8. اختبار النقاط الخطية: ثلاث نقاط$(x_1,y_1)$$(x_2,y_2)$،$(x_3,y_3)$ وتكون متوازية إذا وفقط إذا
  \[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]

مسرد المصطلحات

محدد: تحتوي كل مصفوفة مربعة على رقم حقيقي مرتبط بها يسمى المحدد لها.

رقم ثانوي لمدخل في محدد 3 × 33 × 3: قاصر الإدخال في محدد 3 × 33 × 3 هو محدد 2 × 22 × 2 الذي تم العثور عليه بحذف الصف والعمود في محدد 3 × 33 × 3 الذي يحتوي على الإدخال.

مصفوفة مربعة: المصفوفة المربعة هي مصفوفة لها نفس عدد الصفوف والأعمدة.

محدد

مثال\(\PageIndex{1}\)

مثال\(\PageIndex{2}\)

مثال\(\PageIndex{3}\)

قاصر عند الدخول\(3×3\) A DETERMINANT

مثال\(\PageIndex{4}\)

مثال\(\PageIndex{5}\)

مثال\(\PageIndex{6}\)

التوسع من قبل القاصرين على طول الصف الأول لتقييم\(3×3\) DETERMINANT

مثال\(\PageIndex{7}\)

مثال\(\PageIndex{8}\)

مثال\(\PageIndex{9}\)