4.6: حل أنظمة المعادلات باستخدام المصفوفات

Last updated
Save as PDF

Page ID: 201431

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

اكتب المصفوفة المُعزَّزة لنظام المعادلات
استخدم عمليات الصف على مصفوفة
حل أنظمة المعادلات باستخدام المصفوفات

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

حل:$3(x+2)+4=4(2x−1)+9$.
إذا فاتتك هذه المشكلة، راجع [link].
حل:$0.25p+0.25(x+4)=5.20$.
إذا فاتتك هذه المشكلة، راجع [link].
قم بتقييم متى$x=−2$ و$y=3:2x^2−xy+3y^2$.
إذا فاتتك هذه المشكلة، راجع [link].

اكتب المصفوفة المُعزَّزة لنظام المعادلات

يمكن أن يكون حل نظام المعادلات عملية شاقة حيث يمكن لخطأ بسيط أن يعيث فسادًا في إيجاد الحل. تتوفر طريقة بديلة تستخدم الإجراءات الأساسية للإزالة ولكن مع تدوين أبسط. تتضمن الطريقة استخدام مصفوفة. المصفوفة عبارة عن مصفوفة مستطيلة من الأرقام مرتبة في صفوف وأعمدة.

ماتريكس

المصفوفة عبارة عن مصفوفة مستطيلة من الأرقام مرتبة في صفوف وأعمدة.

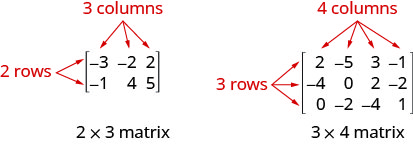
تحتوي المصفوفة التي تحتوي على صفوف m وأعمدة n على ترتيب$m\times n$. تحتوي المصفوفة الموجودة على اليسار أدناه على صفين و 3 أعمدة وبالتالي فهي مرتبة$2\times 3$. نقول إنها مصفوفة 2 × 3.

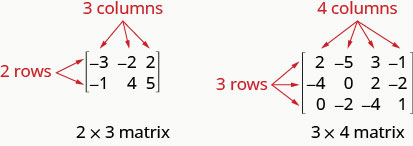
$يوضِّح الشكل مصفوفتين. الرقم الموجود على اليسار يحتوي على الأرقام ناقص 3 وناقص 2 و2 في الصف الأول والأرقام ناقص 1 و4 و5 في الصف الثاني. يتم وضع الصفوف والأعمدة داخل أقواس. وبالتالي، فإنه يحتوي على صفين و 3 أعمدة. يتم تسميته بمصفوفة 2 × 3 أو 2 × 3. المصفوفة الموجودة على اليمين متشابهة ولكن مع 3 صفوف و 4 أعمدة. يتم تصنيفها على مصفوفة 3 × 4.$

كل رقم في المصفوفة يسمى عنصرًا أو إدخالًا في المصفوفة.

سنستخدم مصفوفة لتمثيل نظام المعادلات الخطية. نكتب كل معادلة في الصورة القياسية ومعاملات المتغيرات ويصبح ثابت كل معادلة صفًا في المصفوفة. سيكون كل عمود بعد ذلك معاملات أحد المتغيرات في النظام أو الثوابت. يحل الخط العمودي محل علامات التساوي. نسمي المصفوفة الناتجة المصفوفة المعززة لنظام المعادلات.

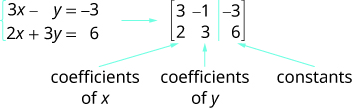
$المعادلات هي 3x زائد y يساوي ناقص 3 و 2x زائد 3y يساوي 6. تظهر مصفوفة 2 × 3. الصف الأول هو 3، 1، ناقص 3. الصف الثاني هو 2، 3، 6. يُطلق على العمود الأول معاملات x. أما العمود الثاني فيسمى معاملات y والثالث باسم الثوابت.$

لاحظ أن العمود الأول يتكون من جميع معاملات x، والعمود الثاني هو جميع معاملات y، والعمود الثالث هو كل الثوابت.

مثال$\PageIndex{1}$

ⓐ$\left\{ \begin{array} {l} 5x−3y=−1 \\ y=2x−2 \end{array} \right. $ ⓑ$ \left\{ \begin{array} {l} 6x−5y+2z=3 \\ 2x+y−4z=5 \\ 3x−3y+z=−1 \end{array} \right. $

إجابة

ⓐ المعادلة الثانية ليست في الشكل القياسي. نعيد كتابة المعادلة الثانية في الشكل القياسي.

\[\begin{aligned} y=2x−2 \\ −2x+y=−2 \end{aligned} \nonumber\]

نستبدل المعادلة الثانية بشكلها القياسي. في المصفوفة المعززة، تعطينا المعادلة الأولى الصف الأول والمعادلة الثانية تعطينا الصف الثاني. يستبدل الخط العمودي علامات المساواة.

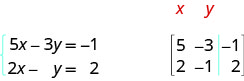
ⓑ جميع المعادلات الثلاث في شكل قياسي. في المصفوفة المعززة، تعطينا المعادلة الأولى الصف الأول، والمعادلة الثانية تعطينا الصف الثاني، والمعادلة الثالثة تعطينا الصف الثالث. يستبدل الخط العمودي علامات المساواة.

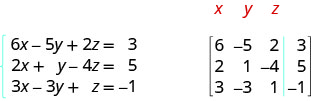
$المعادلات هي 6x ناقص 5y زائد 2z يساوي 3، 2x زائد y ناقص 4z يساوي 5 و 3x ناقص 3y زائد z يساوي ناقص 1. تظهر مصفوفة 4 × 3 يكون الصف الأول فيها 6، ناقص 5، 2، 3. الصف الثاني هو 2، 1، ناقص 4، 5. الصف الثالث هو 3، ناقص 3، 1 وناقص 1. تم تصنيف أعمدتها الثلاثة الأولى x و y و z على التوالي.$

مثال$\PageIndex{2}$

اكتب كل نظام من المعادلات الخطية في صورة مصفوفة معززة:

ⓐ$\left\{ \begin{array} {l} 3x+8y=−3 \\ 2x=−5y−3 \end{array} \right. $ ⓑ$\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right. $

إجابة

ⓐ$\left[ \begin{matrix} 3 &8 &-3 \\ 2 &5 &−3 \end{matrix} \right] $

ⓑ$\left[ \begin{matrix} 2 &3 &1 &−5 \\ −1 &3 &3 &4 \\ 2 &8 &7 &−3 \end{matrix} \right] $

مثال$\PageIndex{3}$

اكتب كل نظام من المعادلات الخطية في صورة مصفوفة معززة:

ⓐ$\left\{ \begin{array} {l} 11x=−9y−5 \\ 7x+5y=−1 \end{array} \right. $ ⓑ$\left\{ \begin{array} {l} 5x−3y+2z=−5 \\ 2x−y−z=4 \\ 3x−2y+2z=−7 \end{array} \right. $

إجابة: ⓐ$\left[ \begin{matrix} 11 &9 &−5 \\ 7 &5 &−1 \end{matrix} \right] $
ⓑ$\left[ \begin{matrix} 5 &−3 &2 &−5 \\ 2 &−1 &−1 &4 \\ 3 &−2 &2 &−7 \end{matrix} \right] $

من المهم أن نحل أنظمة المعادلات باستخدام المصفوفات حتى نتمكن من الانتقال ذهابًا وإيابًا بين النظام والمصفوفة. يطلب منا المثال التالي أخذ المعلومات في المصفوفة وكتابة نظام المعادلات.

مثال$\PageIndex{4}$

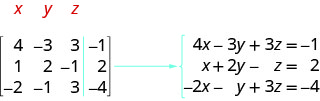
اكتب نظام المعادلات الذي يتوافق مع المصفوفة المعززة:

$\left[ \begin{array} {ccc|c} 4 &−3 &3 &−1 \\ 1 &2 &−1 &2 \\ −2 &−1 &3 &−4 \end{array} \right] $.

إجابة

نتذكر أن كل صف يتوافق مع معادلة وأن كل إدخال هو معامل متغير أو ثابت. يحل الخط العمودي محل علامة المساواة. نظرًا لأن هذه المصفوفة هي a$4\times 3$، فإننا نعلم أنها ستترجم إلى نظام من ثلاث معادلات بثلاثة متغيرات.

$يتم عرض مصفوفة 3 × 4. الصف الأول هو 4، ناقص 3، 3، ناقص 1. الصف الثاني هو 1، 2، ناقص 1، 2. الصف الثالث هو ناقص 2، ناقص 1، 3، ناقص 4. المعادلات الثلاث هي 4x ناقص 3y زائد 3z يساوي ناقص 1، x زائد 2y ناقص z يساوي 2 وناقص 2x ناقص y زائد 3z يساوي ناقص 4.$

مثال$\PageIndex{5}$

اكتب نظام المعادلات الذي يتوافق مع المصفوفة المعززة:$\left[ \begin{matrix} 1 &−1 &2 &3 \\ 2 &1 &−2 &1 \\ 4 &−1 &2 &0 \end{matrix} \right] $.

إجابة: $\left\{ \begin{array} {l} x−y+2z=3 \\ 2x+y−2z=1 \\ 4x−y+2z=0 \end{array} \right.$

مثال$\PageIndex{6}$

اكتب نظام المعادلات الذي يتوافق مع المصفوفة المعززة:$\left[ \begin{matrix} 1 &1 &1 &4 \\ 2 &3 &−1 &8 \\ 1 &1 &−1 &3 \end{matrix} \right] $.

إجابة: $\left\{ \begin{array} {l} x+y+z=4 \\ 2x+3y−z=8 \\ x+y−z=3 \end{array} \right.$

استخدم عمليات الصف على مصفوفة

بمجرد أن يصبح نظام المعادلات في شكل مصفوفة معززة، سنقوم بإجراء عمليات على الصفوف التي ستقودنا إلى الحل.

لحل المعادلات بالحذف، لا يهم الترتيب الذي نضع به المعادلات في النظام. وبالمثل، في المصفوفة يمكننا تبادل الصفوف.

عندما نحلّ عن طريق الحذف، غالبًا ما نضرب إحدى المعادلات في ثابت. نظرًا لأن كل صف يمثل معادلة، ويمكننا ضرب كل طرف من المعادلة بثابت، وبالمثل يمكننا ضرب كل إدخال في صف بأي رقم حقيقي باستثناء 0.

في الحذف، غالبًا ما نضيف مضاعفًا لصف واحد إلى صف آخر. في المصفوفة، يمكننا استبدال صف بمجموعه بمضاعفات صف آخر.

تسمى هذه الإجراءات عمليات الصف وستساعدنا في استخدام المصفوفة لحل نظام المعادلات.

عمليات الصف

في المصفوفة، يمكن تنفيذ العمليات التالية على أي صف وستكون المصفوفة الناتجة مكافئة للمصفوفة الأصلية.

قم بتبادل أي صفين.
اضرب صفًا بأي رقم حقيقي باستثناء 0.
أضف مضاعفًا غير صفري لصف واحد إلى صف آخر.

من السهل القيام بهذه العمليات ولكن كل العمليات الحسابية يمكن أن تؤدي إلى خطأ. إذا استخدمنا نظامًا لتسجيل عملية الصف في كل خطوة، فمن الأسهل بكثير العودة والتحقق من عملنا.

نحن نستخدم الأحرف الكبيرة مع المقتطفات لتمثيل كل صف. ثم نعرض العملية على يسار المصفوفة الجديدة. لإظهار تبادل صف:

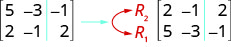
$تظهر مصفوفة 2 × 3. الصف الأول المسمى R2 هو 2، ناقص 1، 2. الصف الثاني المسمى R1 هو 5، ناقص 3، ناقص 1.$

لضرب الصف 2 من خلال$−3$:

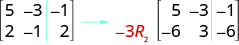
$تظهر مصفوفة 2 × 3. الصف الأول هو 5، ناقص 3، ناقص 1. الصف الثاني هو 2، ناقص 1، 2. نقطة سهم من هذه المصفوفة إلى أخرى على اليمين. الصف الأول من المصفوفة الجديدة هو نفسه. يسبق الصف الثاني ناقص 3 R2. إنه ناقص 6، 3، ناقص 6.$

لضرب الصف 2$−3$ وإضافته إلى الصف 1:

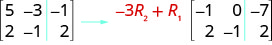
$تظهر مصفوفة 2 × 3. الصف الأول هو 5، ناقص 3، ناقص 1. الصف الثاني هو 2، ناقص 1، 2. نقطة سهم من هذه المصفوفة إلى أخرى على اليمين. يسبق الصف الأول من المصفوفة الجديدة ناقص 3 R2 بالإضافة إلى R1. إنه ناقص 1، 0، ناقص 7. الصف الثاني هو 2، ناقص 1، 2.$

مثال$\PageIndex{7}$

قم بإجراء العمليات المشار إليها على المصفوفة المعززة:

ⓐ تبادل الصفوف 2 و 3.

ⓑ اضرب الصف 2 في 5.

$ \left[ \begin{array} {ccc|c} 6 &−5 &2 &3 \\ 2 &1 &−4 &5 \\ 3 &−3 &1 &−1 \end{array} \right] $

إجابة

ⓐ نقوم بتبادل الصفوف 2 و 3.

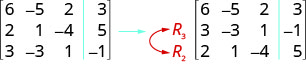
$يتم عرض مصفوفتين 3 × 4. في الصف الموجود على اليسار، الصف الأول هو 6، ناقص 5، 2، 3. الصف الثاني هو 2، 1، ناقص 4، 5. الصف الثالث هو 3، ناقص 3، 1، ناقص 1. المصفوفة الثانية متشابهة باستثناء أن الصفوف 2 و 3 متبادلان.$

ⓑ نضرب الصف 2 في 5.

$يتم عرض مصفوفتين 3 × 4. في الصف الموجود على اليسار، الصف الأول هو 6، ناقص 5، 2، 3. الصف الثاني هو 2، 1، ناقص 4، 5. الصف الثالث هو 3، ناقص 3، 1، ناقص 1. المصفوفة الثانية مشابهة للأولى باستثناء أن الصف 2، الذي يسبقه 5 R2، هو 10، 5، ناقص 20، 25.$

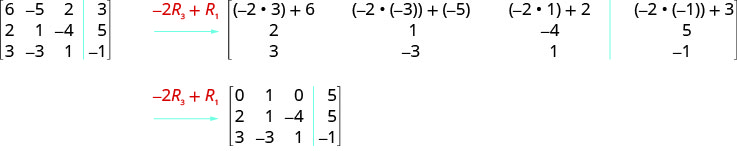
$في مصفوفة 3 × 4، الصف الأول هو 6، ناقص 5، 2، 3. الصف الثاني هو 2، 1، ناقص 4، 5. الصف الثالث هو 3، ناقص 3، 1، ناقص 1. عند إجراء العملية ناقص 2 R3 بالإضافة إلى R1 في الصف الأول، يصبح الصف الأول 6 زائد ناقص 2 في 3، ناقص 5 زائد ناقص 2 مرات ناقص 3، 2 زائد ناقص 2 في 1 و 3 زائد ناقص 2 مرات ناقص 1. يصبح هذا 0، 1، 0، 5. الصفان المتبقيان من المصفوفة الجديدة هما نفس الشيء.$

مثال$\PageIndex{8}$

قم بإجراء العمليات المشار إليها على المصفوفة المعززة:

ⓐ تبادل الصفوف 1 و 3.

ⓑ اضرب الصف 3 في 3.

$ \left[ \begin{array} {ccc|c} 5 &−2 &-2 &-2 \\ 4 &-1 &−4 &4 \\ -2 &3 &0 &−1 \end{array} \right] $

إجابة

ⓐ$ \left[ \begin{matrix} −2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 5 &−2 &−2 &−2 \end{matrix} \right] $

ⓑ$ \left[ \begin{matrix} −2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 15 &−6 &−6 &−6 \end{matrix} \right] $

ⓒ$ \left[ \begin{matrix} -2 &3 &0 &2 & \\ 3 &4 &-13 &-16 &-8 \\ 15 &-6 &-6 &-6 & \end{matrix} \right] $

مثال$\PageIndex{9}$

قم بإجراء العمليات المشار إليها على المصفوفة المعززة:

ⓐ تبادل الصفوف 1 و 2،

ⓑ اضرب الصف 1 في 2،

$ \left[ \begin{array} {ccc|c} 2 &−3 &−2 &−4 \\ 4 &1 &−3 &2 \\ 5 &0 &4 &−1 \end{array} \right] $

إجابة: ⓐ$ \left[ \begin{matrix} 4 &1 &−3 &2 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] $
ⓑ$ \left[ \begin{matrix} 8 &2 &−6 &4 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] $
ⓒ$ \left[ \begin{matrix} 14 &−7 &−12 &−8 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] $

الآن بعد أن مارسنا عمليات الصف، سننظر إلى المصفوفة المعززة ونكتشف العملية التي سنستخدمها للوصول إلى الهدف. هذا هو بالضبط ما فعلناه عندما قمنا بالإزالة. لقد قررنا الرقم الذي يجب ضرب الصف به حتى يتم التخلص من المتغير عندما نضيف الصفوف معًا.

بالنظر إلى هذا النظام، ماذا ستفعل للقضاء على x؟

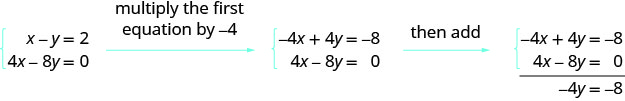
$المعادلتان هما x ناقص y يساوي 2 و 4x ناقص 8y يساوي 0. بضرب الأول في ناقص 4، نحصل على ناقص 4x زائد 4y يساوي ناقص 8. بإضافة هذا إلى المعادلة الثانية نحصل على ناقص 4y يساوي ناقص 8.$

هذا المثال التالي يفعل نفس الشيء بشكل أساسي، ولكن للمصفوفة.

مثال$\PageIndex{10}$

قم بإجراء عملية الصف المطلوبة التي ستجعل الإدخال الأول في الصف 2 صفرًا في المصفوفة المعززة:$ \left[ \begin{array} {cc|c} 1 &−1 &2 \\ 4 &−8 &0 \end{array} \right] $

إجابة

لجعل 4 a 0، يمكننا ضرب الصف 1 في$−4$ ثم إضافته إلى الصف 2.

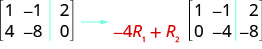
$المصفوفة 2 × 3 هي 1، ناقص 1، 2 و 4، ناقص 8، 0. عند تنفيذ العملية ناقص 4R1 بالإضافة إلى R2 في الصف 2، يصبح الصف الثاني من المصفوفة الجديدة 0، ناقص 4، ناقص 8. يبقى الصف الأول هو نفسه.$

مثال$\PageIndex{11}$

قم بإجراء عملية الصف المطلوبة التي ستجعل الإدخال الأول في الصف 2 صفرًا في المصفوفة المعززة:$ \left[ \begin{array} {cc|c} 1 &−1 &2 \\ 3 &−6 &2 \end{array} \right] $

إجابة: $ \left[ \begin{matrix} 1 &−1 &2 \\ 0 &−3 &−4 \end{matrix} \right] $

مثال$\PageIndex{12}$

قم بإجراء عملية الصف المطلوبة التي ستجعل الإدخال الأول في الصف 2 صفرًا في المصفوفة المعززة:$ \left[ \begin{array} {cc|c} 1 &−1 &3 \\ -2 &−3 &2 \end{array} \right] $

إجابة: $ \left[ \begin{matrix} 1 &−1 &3 \\ 0 &−5 &8 \end{matrix} \right] $

حل أنظمة المعادلات باستخدام المصفوفات

لحل نظام المعادلات باستخدام المصفوفات، نقوم بتحويل المصفوفة المُعزَّزة إلى مصفوفة في شكل درجات صفية باستخدام العمليات الصفية. بالنسبة لنظام المعادلات المتسق والمستقل، تكون المصفوفة المعززة في شكل درجات صفية عندما يكون كل إدخال على القطر على يسار الخط العمودي هو 1 وجميع الإدخالات الموجودة أسفل القطر هي الأصفار.

نموذج الصف

بالنسبة لنظام المعادلات المتسق والمستقل، تكون المصفوفة المعززة في شكل درجات صفية عندما يكون كل إدخال على القطر على يسار الخط العمودي هو 1 وجميع الإدخالات الموجودة أسفل القطر هي الأصفار.

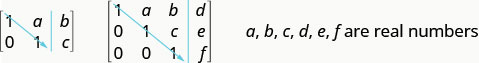
$تظهر مصفوفة 2 × 3 على اليسار. الصف الأول هو 1، a، b. الصف الثاني هو 0، 1، c. يشير السهم قطريًا لأسفل ولليمين، ويتداخل مع كل من 1s في المصفوفة. تظهر مصفوفة 3 × 4 على اليمين. الصف الأول هو 1، أ، ب، د. صفه الثاني هو 0، 1، ج، هـ. صفه الثالث هو 0، 0، 1، f. يشير السهم قطريًا لأسفل ولليمين، متداخلًا مع كل الأحرف الأولى في المصفوفة. a، b، c، d، e، f هي أعداد حقيقية.$

بمجرد أن نحصل على المصفوفة المعززة في شكل درجات الصف، يمكننا كتابة نظام المعادلات المكافئ وقراءة قيمة متغير واحد على الأقل. ثم نستبدل هذه القيمة في معادلة أخرى لمواصلة حل المتغيرات الأخرى. يتم توضيح هذه العملية في المثال التالي.

كيفية حل نظام المعادلات باستخدام المصفوفة

حل نظام المعادلات باستخدام مصفوفة:$\left\{ \begin{array} {l} 3x+4y=5 \\ x+2y=1 \end{array} \right. $

إجابة: $المعادلات هي 3x زائد 4y يساوي 5 و x زائد 2y يساوي 1. الخطوة 1. اكتب المصفوفة المعزَّزة لنظام المعادلات. نحصل على مصفوفة 2 × 3 مع الصف الأول 3، 4، 5 والصف الثاني 1، 2، 1.$ $الخطوة 2. باستخدام عمليات الصف، يصبح الإدخال في الصف 1، العمود 1 هو 1. قم بتبادل الصفوف R1 وR2.$ $الخطوة 3. باستخدام عمليات الصف، احصل على الأصفار في العمود 1 أسفل الرقم 1. اضرب الصف 1 في ناقص 3 وأضفه إلى الصف 2. يصبح الصف 2 0، ناقص 2، 2.$ $الخطوة 4. باستخدام عمليات الصف، اجعل الإدخال في الصف 2، العمود 2 هو 1. اضرب الصف 2 في ناقص النصف. يصبح الصف 2 0، 1، ناقص 1.$ $الخطوة 5. استمر في العملية حتى تصبح المصفوفة في شكل درجات الصف. المصفوفة الآن في شكل درجات صفية.$ $الخطوة 6. اكتب نظام المعادلات المقابل. نحصل على x زائد 2y يساوي 1 و y يساوي ناقص 1.$ $الخطوة 7. استخدم الاستبدال للعثور على المتغيرات المتبقية. البديل y يساوي سالب 1 إلى x زائد 2y يساوي 1. X زائد 2 في سالب 1 يساوي 1. X ناقص 2 يساوي 1. نحصل على x يساوي 3.$ $الخطوة 8. اكتب الحل كزوج مرتب أو ثلاثي. الزوج المطلوب هو (3، سلبي 1).$ $الخطوة 9. تحقق من أن الحل يجعل المعادلات الأصلية صحيحة.$

مثال$\PageIndex{14}$

حل نظام المعادلات باستخدام مصفوفة:$\left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. $

إجابة: الحل هو$(4,−1)$.

مثال$\PageIndex{15}$

حل نظام المعادلات باستخدام مصفوفة:$\left\{ \begin{array} {l} 2x+y=−4 \\ x−y=−2 \end{array} \right. $

إجابة: الحل هو$(−2,0)$.

يتم تلخيص الخطوات هنا.

حل نظام المعادلات باستخدام المصفوفات.

اكتب المصفوفة المعزَّزة لنظام المعادلات.
باستخدام عمليات الصف، يصبح الإدخال في الصف 1، العمود 1 هو 1.
باستخدام عمليات الصف، احصل على الأصفار في العمود 1 أسفل الرقم 1.
باستخدام عمليات الصف، اجعل الإدخال في الصف 2، العمود 2 هو 1.
استمر في العملية حتى تصبح المصفوفة في شكل درجات الصف.
اكتب نظام المعادلات المقابل.
استخدم الاستبدال للعثور على المتغيرات المتبقية.
اكتب الحل كزوج مرتب أو ثلاثي.
تحقق من أن الحل يجعل المعادلات الأصلية صحيحة.

في ما يلي صورة مرئية لإظهار ترتيب الحصول على 1 و 0 في الموضع المناسب لنموذج الصفوف.

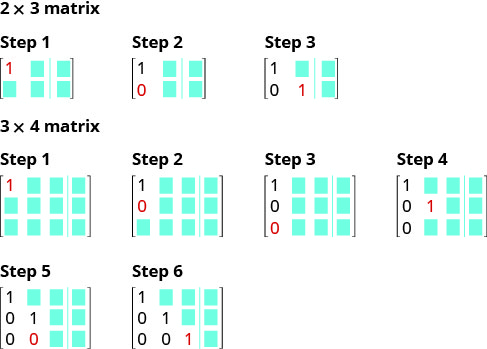
$يوضح الشكل 3 خطوات لمصفوفة 2 × 3 و 6 خطوات لمصفوفة 3 × 4. بالنسبة للأولى، الخطوة 1 هي الحصول على 1 في الصف 1 في العمود 1. الخطوة الأولى هي الحصول على 0 هو الصف 2 العمود 1. الخطوة 3 هي الحصول على 1 في الصف 2 العمود 2. بالنسبة لمصفوفة 3 × 4، تتمثل الخطوة 1 في الحصول على 1 في الصف 1 في العمود 1. الخطوة 2 هي الحصول على 0 في الصف 2 العمود 1. الخطوة 3 هي الحصول على 0 في الصف 3 العمود 1. الخطوة 4 هي الحصول على 1 في الصف 2 العمود 2. الخطوة 5 هي الحصول على 0 في الصف 3 العمود 2. الخطوة 6 هي الحصول على 1 في الصف 3 العمود 3.$

نستخدم نفس الإجراء عندما يحتوي نظام المعادلات على ثلاث معادلات.

مثال$\PageIndex{16}$

حل نظام المعادلات باستخدام مصفوفة:$\left\{ \begin{array} {l} 3x+8y+2z=−5 \\ 2x+5y−3z=0 \\ x+2y−2z=−1 \end{array} \right. $

إجابة

	$.$
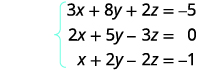
اكتب المصفوفة المعزَّزة للمعادلات.	$.$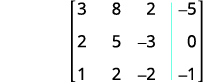
قم بتبادل الصفين 1 و 3 للحصول على الإدخال في الصف 1، العمود 1 ليكون 1.	$.$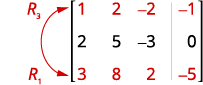
باستخدام عمليات الصف، احصل على الأصفار في العمود 1 أسفل الرقم 1.	$.$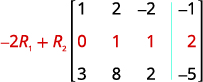
	$.$
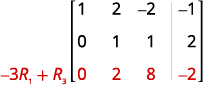
الإدخال في الصف 2، العمود 2 هو الآن 1.
استمر في العملية حتى تصبح المصفوفة في شكل درجات الصف.	$.$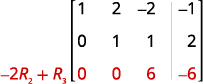
	$.$
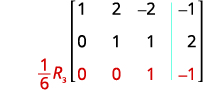
المصفوفة الآن في شكل درجات صفية.	$.$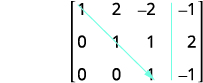
اكتب نظام المعادلات المقابل.	$.$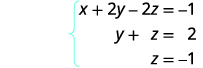
استخدم الاستبدال للعثور على المتغيرات المتبقية.	$.$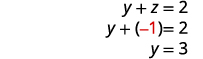
	$.$ $.$
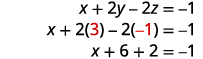
اكتب الحل كزوج مرتب أو ثلاثي.	$.$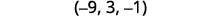
تحقق من أن الحل يجعل المعادلات الأصلية صحيحة.	نترك الشيك لك.

مثال$\PageIndex{17}$

حل نظام المعادلات باستخدام مصفوفة:$\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right. $

إجابة: $(6,−1,−3)$

مثال$\PageIndex{18}$

حل نظام المعادلات باستخدام مصفوفة:$\left\{ \begin{array} {l} −3x+y+z=−4 \\ −x+2y−2z=1 \\ 2x−y−z=−1 \end{array} \right. $

إجابة: $(5,7,4)$

حتى الآن كان عملنا مع المصفوفات مع الأنظمة المتسقة والمستقلة فقط، مما يعني أن لديهم حلًا واحدًا تمامًا. دعونا الآن نلقي نظرة على ما يحدث عندما نستخدم مصفوفة لنظام تابع أو غير متناسق.

مثال$\PageIndex{19}$

حل نظام المعادلات باستخدام مصفوفة:$\left\{ \begin{array} {l} x+y+3z=0 \\ x+3y+5z=0 \\ 2x+4z=1 \end{array} \right. $

إجابة

	$.$
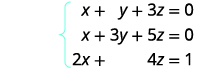
اكتب المصفوفة المعزَّزة للمعادلات.	$.$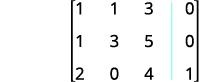
الإدخال في الصف 1، العمود 1 هو 1.
باستخدام عمليات الصف، احصل على الأصفار في العمود 1 أسفل الرقم 1.	$.$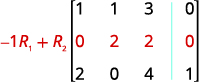
	$.$
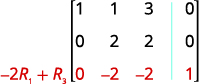
استمر في العملية حتى تصبح المصفوفة في شكل درجات الصف.	$.$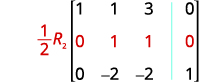
اضرب الصف 2 في 2 وأضفه إلى الصف 3.	$.$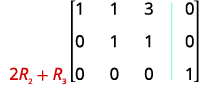
في هذه المرحلة، لدينا جميع الأصفار على يسار الصف 3.
اكتب نظام المعادلات المقابل.	$.$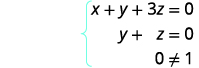
بما أن$0 \neq 1 $ لدينا بيانًا كاذبًا. تمامًا كما هو الحال عندما قمنا بحل نظام باستخدام طرق أخرى، فإن هذا يخبرنا أن لدينا نظامًا غير متناسق. لا يوجد حل.

مثال$\PageIndex{20}$

حل نظام المعادلات باستخدام مصفوفة:$\left\{ \begin{array} {l} x−2y+2z=1 \\ −2x+y−z=2 \\ x−y+z=5 \end{array} \right. $

إجابة: لا يوجد حل

مثال$\PageIndex{21}$

حل نظام المعادلات باستخدام مصفوفة:$\left\{ \begin{array} {l} 3x+4y−3z=−2 \\ −2x+3y−z=−1 \\ 2x+y−2z=6 \end{array} \right. $

إجابة: لا يوجد حل

كان النظام الأخير غير متسق وبالتالي لم يكن لديه حلول. المثال التالي يعتمد ولديه العديد من الحلول بلا حدود.

مثال$\PageIndex{22}$

حل نظام المعادلات باستخدام مصفوفة:$\left\{ \begin{array} {l} x−2y+3z=1 \\ x+y−3z=7 \\ 3x−4y+5z=7 \end{array} \right. $

إجابة

	$.$
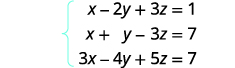
اكتب المصفوفة المعزَّزة للمعادلات.	$.$
الإدخال في الصف 1، العمود 1 هو 1.
باستخدام عمليات الصف، احصل على الأصفار في العمود 1 أسفل الرقم 1.	$.$
	$.$
استمر في العملية حتى تصبح المصفوفة في شكل درجات الصف.	$.$
اضرب الصف 2$−2$ وأضفه إلى الصف 3.	$.$
في هذه المرحلة، لدينا جميع الأصفار في الصف السفلي.
اكتب نظام المعادلات المقابل.	$.$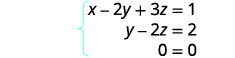
بما أن$0=0$ لدينا بيانًا حقيقيًا. تمامًا كما هو الحال عندما قمنا بالحل عن طريق الاستبدال، يخبرنا هذا أن لدينا نظامًا تابعًا. هناك العديد من الحلول بلا حدود.
حل لـ y بدلالة z في المعادلة الثانية.	$.$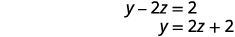
حل المعادلة الأولى لـ x بدلالة z.	$.$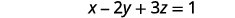
بديل$y=2z+2$.	$.$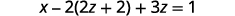
قم بالتبسيط.	$.$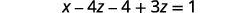
قم بالتبسيط.	$.$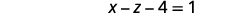
قم بالتبسيط.	$.$
يحتوي النظام على العديد من الحلول$(x,y,z)$، حيث$x=z+5;\space y=2z+2;\space z$ يوجد أي رقم حقيقي.

مثال$\PageIndex{23}$

حل نظام المعادلات باستخدام مصفوفة:$\left\{ \begin{array} {l} x+y−z=0 \\ 2x+4y−2z=6 \\ 3x+6y−3z=9 \end{array} \right. $

إجابة: العديد من الحلول بلا حدود$(x,y,z)$، أين$x=z−3;\space y=3;\space z$ يوجد أي رقم حقيقي.

مثال$\PageIndex{24}$

حل نظام المعادلات باستخدام مصفوفة:$\left\{ \begin{array} {l} x−y−z=1 \\ −x+2y−3z=−4 \\ 3x−2y−7z=0 \end{array} \right. $

إجابة: العديد من الحلول بلا حدود$(x,y,z)$، أين$x=5z−2;\space y=4z−3;\space z$ يوجد أي رقم حقيقي.

قم بالوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات وممارسة إضافية مع Gaussian Elimation

إقصاء غاوسي

المفاهيم الرئيسية

المصفوفة: المصفوفة عبارة عن مصفوفة مستطيلة من الأرقام مرتبة في صفوف وأعمدة. تحتوي المصفوفة التي تحتوي على صفوف m وأعمدة n على ترتيب$m\times n$. تحتوي المصفوفة الموجودة على اليسار أدناه على صفين و 3 أعمدة وبالتالي فهي مرتبة$2\times 3$. نقول إنها مصفوفة 2 × 3.
$يوضِّح الشكل مصفوفتين. الرقم الموجود على اليسار يحتوي على الأرقام ناقص 3 وناقص 2 و2 في الصف الأول والأرقام ناقص 1 و4 و5 في الصف الثاني. يتم وضع الصفوف والأعمدة داخل أقواس. وبالتالي، فإنه يحتوي على صفين و 3 أعمدة. يتم تسميته بمصفوفة 2 × 3 أو 2 × 3. المصفوفة الموجودة على اليمين متشابهة ولكن مع 3 صفوف و 4 أعمدة. يتم تصنيفها على مصفوفة 3 × 4.$
كل رقم في المصفوفة يسمى عنصرًا أو إدخالًا في المصفوفة.
عمليات الصف: في المصفوفة، يمكن تنفيذ العمليات التالية على أي صف وستكون المصفوفة الناتجة معادلة للمصفوفة الأصلية.
- قم بتبادل أي صفين
- اضرب صفًا بأي رقم حقيقي باستثناء 0
- أضف مضاعفًا غير صفري لصف واحد إلى صف آخر
نموذج Row-Echelon: بالنسبة لنظام معادلات متسق ومستقل، تكون المصفوفة المعززة في صورة صفية درجية عندما يكون كل إدخال على القطر على يسار الخط العمودي هو 1 وجميع الإدخالات الموجودة أسفل القطر هي الأصفار.
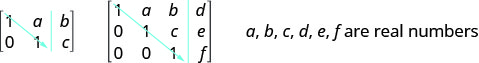
$يوضِّح الشكل مصفوفتين. الرقم الموجود على اليسار يحتوي على الأرقام ناقص 3 وناقص 2 و2 في الصف الأول والأرقام ناقص 1 و4 و5 في الصف الثاني. يتم وضع الصفوف والأعمدة داخل أقواس. وبالتالي، فإنه يحتوي على صفين و 3 أعمدة. يتم تسميته بمصفوفة 2 × 3 أو 2 × 3. المصفوفة الموجودة على اليمين متشابهة ولكن مع 3 صفوف و 4 أعمدة. يتم تصنيفها على مصفوفة 3 × 4.$
كيفية حل نظام المعادلات باستخدام المصفوفات.
1. اكتب المصفوفة المعزَّزة لنظام المعادلات.
2. باستخدام عمليات الصف، يصبح الإدخال في الصف 1، العمود 1 هو 1.
3. باستخدام عمليات الصف، احصل على الأصفار في العمود 1 أسفل الرقم 1.
4. باستخدام عمليات الصف، اجعل الإدخال في الصف 2، العمود 2 هو 1.
5. استمر في العملية حتى تصبح المصفوفة في شكل درجات الصف.
6. اكتب نظام المعادلات المقابل.
7. استخدم الاستبدال للعثور على المتغيرات المتبقية.
8. اكتب الحل كزوج مرتب أو ثلاثي.
9. تحقق من أن الحل يجعل المعادلات الأصلية صحيحة.

مسرد المصطلحات

مصفوفة: المصفوفة عبارة عن مصفوفة مستطيلة من الأرقام مرتبة في صفوف وأعمدة.

شكل الصف: تكون المصفوفة في شكل صفي درالي عندما تكون على يسار الخط العمودي، ويكون كل إدخال على القطر 1 وجميع الإدخالات الموجودة أسفل القطر تساوي أصفرًا.

ماتريكس

مثال\(\PageIndex{1}\)

مثال\(\PageIndex{2}\)

مثال\(\PageIndex{3}\)

مثال\(\PageIndex{4}\)

مثال\(\PageIndex{5}\)

مثال\(\PageIndex{6}\)

عمليات الصف

مثال\(\PageIndex{7}\)

مثال\(\PageIndex{8}\)

مثال\(\PageIndex{9}\)

مثال\(\PageIndex{10}\)

مثال\(\PageIndex{11}\)

مثال\(\PageIndex{12}\)

نموذج الصف

كيفية حل نظام المعادلات باستخدام المصفوفة

مثال\(\PageIndex{14}\)

مثال\(\PageIndex{15}\)

حل نظام المعادلات باستخدام المصفوفات.

مثال\(\PageIndex{16}\)

مثال\(\PageIndex{17}\)

مثال\(\PageIndex{18}\)

مثال\(\PageIndex{19}\)

مثال\(\PageIndex{20}\)

مثال\(\PageIndex{21}\)

مثال\(\PageIndex{22}\)

مثال\(\PageIndex{23}\)

مثال\(\PageIndex{24}\)