4.2: حل أنظمة المعادلات الخطية بمتغيرين
- Page ID
- 201484
في نهاية هذا القسم، ستكون قادرًا على:
- حدِّد ما إذا كان الزوج المُرتَّب حلًا لنظام المعادلات
- حل نظام المعادلات الخطية بالرسم البياني
- حل نظام المعادلات عن طريق الاستبدال
- حل نظام المعادلات بالحذف
- اختر الطريقة الأكثر ملاءمة لحل نظام المعادلات الخطية
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
حدِّد إذا ما كان الزوج المُرتَّب حلًا لنظام المعادلات
في حل المعادلات الخطية، تعلمنا كيفية حل المعادلات الخطية بمتغير واحد. الآن سنعمل مع معادلتين خطيتين أو أكثر مجمعة معًا، والتي تُعرف باسم نظام المعادلات الخطية.
عندما يتم تجميع معادلتين خطيتين أو أكثر معًا، فإنها تشكل نظامًا من المعادلات الخطية.
في هذا القسم، سنركز عملنا على أنظمة معادلتين خطيتين في جهلين. سنحل أنظمة أكبر من المعادلات لاحقًا في هذا الفصل.
فيما يلي مثال لنظام معادلتين خطيتين. نستخدم قوسًا لإظهار أن المعادلتين مجمعتان معًا لتشكيل نظام من المعادلات.
\[ \left\{ \begin{aligned} 2x+y & = 7 \\ x−2y & = 6 \end{aligned} \right. \nonumber \]
تحتوي المعادلة الخطية المكونة من متغيرين، مثل\(2x+y=7\)، على عدد لا نهائي من الحلول. الرسم البياني الخاص به هو خط. تذكر أن كل نقطة على الخط هي حل للمعادلة وكل حل للمعادلة هو نقطة على الخط.
لحل نظام من معادلتين خطيتين، نريد أن نجد قيم المتغيرات التي تمثل حلولًا لكلتا المعادلتين. بمعنى آخر، نحن نبحث عن الأزواج المرتبة\((x,y)\) التي تجعل كلا المعادلتين صحيحتين. هذه تسمى حلول نظام المعادلات.
حلول نظام المعادلات هي قيم المتغيرات التي تجعل جميع المعادلات صحيحة. يتم تمثيل حل نظام من معادلتين خطيتين بزوج مرتب\((x,y)\).
لتحديد ما إذا كان الزوج المرتب حلاً لنظام من معادلتين، فإننا نستبدل قيم المتغيرات في كل معادلة. إذا كان الزوج الذي تم ترتيبه يجعل كلتا المعادلتين صحيحتين، فهذا حل للنظام.
حدد ما إذا كان الزوج المطلوب حلاً للنظام\(\left \{ \begin{array} {l} x−y = −1 \\ 2x−y = −5 \end{array} \right. \).
ⓐ\((−2,−1)\) ⓑ\((−4,−3)\)
- إجابة
-
ⓐ
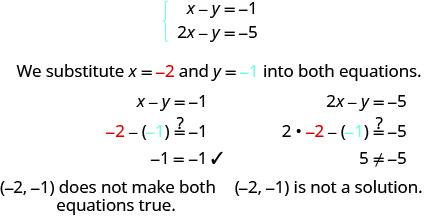
ⓑ
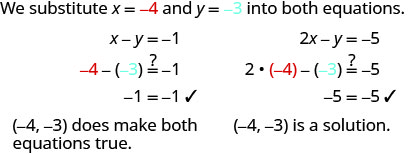
حدد ما إذا كان الزوج المطلوب حلاً للنظام\(\left \{ \begin{array} 3x+y = 0 \\ x+2y = −5 \end{array} \right. \).
ⓐ\((1,−3)\) ⓑ\((0,0)\)
- إجابة
-
ⓐ نعم ⓑ لا
حدد ما إذا كان الزوج المطلوب حلاً للنظام\(\left \{ \begin{array} x−3y = −8 \\ −3x−y = 4 \end{array} \right. \).
ⓐ\((2,−2)\) ⓑ\((−2,2)\)
- إجابة
-
ⓐ لا ⓑ نعم
حل نظام المعادلات الخطية بالرسم البياني
في هذا القسم، سنستخدم ثلاث طرق لحل نظام المعادلات الخطية. الطريقة الأولى التي سنستخدمها هي الرسم البياني.
الرسم البياني للمعادلة الخطية هو خط. كل نقطة على الخط هي حل للمعادلة. بالنسبة لنظام مكون من معادلتين، سنرسم خطين. ثم يمكننا رؤية جميع النقاط التي تمثل حلولًا لكل معادلة. ومن خلال إيجاد القواسم المشتركة بين السطور، سنجد الحل للنظام.
تحتوي معظم المعادلات الخطية في متغير واحد على حل واحد، لكننا رأينا أن بعض المعادلات، التي تسمى التناقضات، ليس لها حلول، وبالنسبة للمعادلات الأخرى، التي تسمى الهويات، فإن جميع الأرقام هي حلول.
وبالمثل، عندما نحل نظامًا من معادلتين خطيتين يمثلهما رسم بياني من سطرين في نفس المستوى، هناك ثلاث حالات محتملة، كما هو موضح.
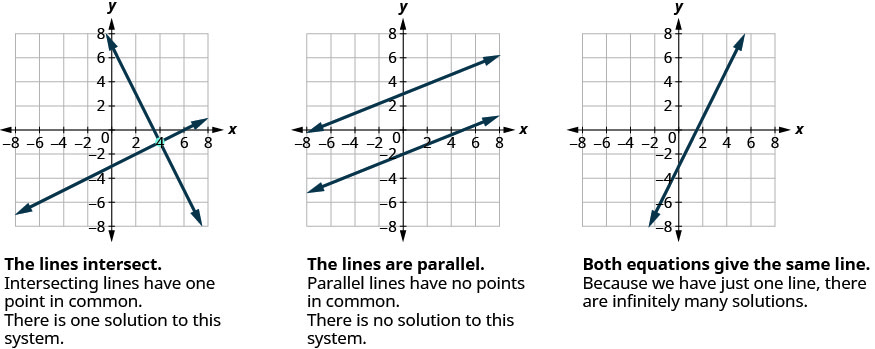
في كل مرة نعرض فيها طريقة جديدة، سنستخدمها على نفس نظام المعادلات الخطية. في نهاية القسم، ستقرر الطريقة الأكثر ملاءمة لحل هذا النظام.
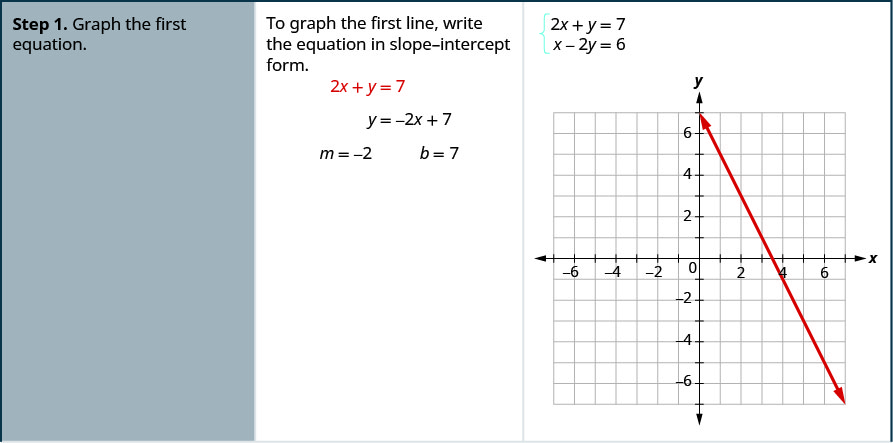
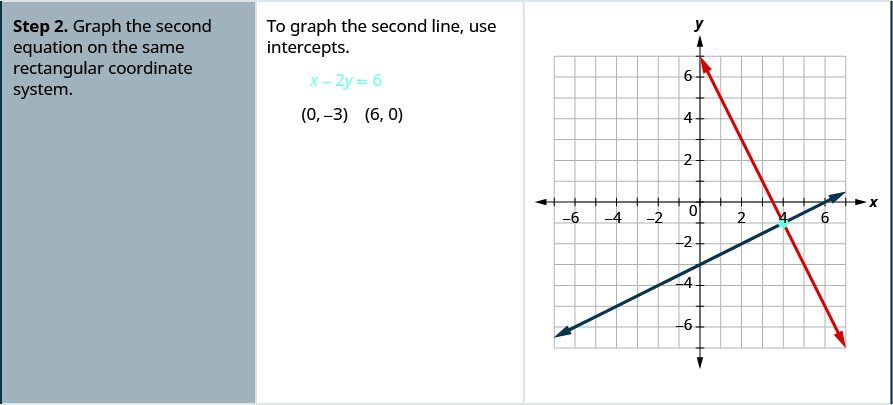
حل النظام عن طريق الرسوم البيانية\( \left\{ \begin{array} {l} 2x+y = 7 \\ x−2y = 6 \end{array} \right. \).
- إجابة
-


حل النظام عن طريق الرسم البياني:\( \left\{ \begin{array} {l} x−3y = −3 \\ x+y = 5 \end{array} \right. \).
- إجابة
-
\((3,2)\)
حل النظام عن طريق الرسم البياني:\( \left\{ \begin{array} {l} −x+y = 1 \\ 3x+2y = 12 \end{array} \right.\)
- إجابة
-
\((2,3)\)
تظهر هنا الخطوات التي يجب استخدامها لحل نظام المعادلات الخطية بالرسوم البيانية.
- ارسم المعادلة الأولى بيانيًا.
- ارسم المعادلة الثانية على نفس نظام الإحداثيات المستطيلة.
- حدد ما إذا كانت الخطوط تتقاطع أو متوازية أو هي نفس الخط.
- حدد الحل للنظام.
- في حالة تقاطع الخطوط، حدد نقطة التقاطع. هذا هو الحل للنظام.
- إذا كانت الخطوط متوازية، فلن يكون لدى النظام أي حل.
- إذا كانت الخطوط هي نفسها، فإن النظام يحتوي على عدد لا نهائي من الحلول.
- تحقق من الحل في كلتا المعادلتين.
في المثال التالي، سنقوم أولاً بإعادة كتابة المعادلات في شكل منحدر - مقطع لأن هذا سيسهل علينا رسم الخطوط بسرعة.
حل النظام عن طريق الرسم البياني:\(\left\{ \begin{array} {l} 3x+y = −1 \\ 2x+y = 0 \end{array}\right.\)
- إجابة
-
سنقوم بحل هاتين المعادلتين\(y\) حتى نتمكن من رسم بياني لهما بسهولة باستخدام منحدرهما\(y\) وقطعتهما.
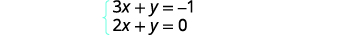
حل المعادلة الأولى لـ y. 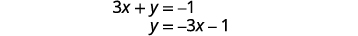
ابحث عن المنحدر ونقطة التقاطع y. 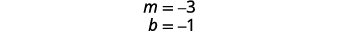
حل المعادلة الثانية لـ y. 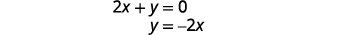
ابحث عن المنحدر ونقطة التقاطع y. 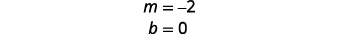
رسم الخطوط بيانيًا. 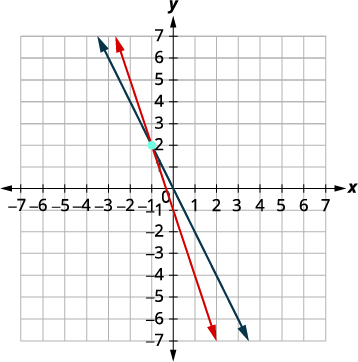
حدد نقطة التقاطع. تتقاطع الخطوط عند\((−1,2)\). تحقق من الحل في كلتا المعادلتين.
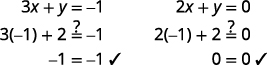
الحل هو\((−1,2)\).
حل النظام عن طريق الرسم البياني:\(\left\{ \begin{array} {l} −x+y = 1 \\2x+y = 10 \end{array}\right. \).
- إجابة
-
\((3,4)\)
حل النظام عن طريق الرسم البياني:\(\left\{ \begin{array} {l} 2x+y = 6 \\x+y = 1 \end{array}\right. \).
- إجابة
-
\((5,−4)\)
في جميع أنظمة المعادلات الخطية حتى الآن، تقاطعت الخطوط وكان الحل نقطة واحدة. في المثالين التاليين، سننظر إلى نظام المعادلات الذي ليس له حل ونظام المعادلات الذي يحتوي على عدد لا نهائي من الحلول.
حل النظام عن طريق الرسم البياني:\(\left\{ \begin{array} {l} y = \tfrac{1}{2}x-3 \\ x-2y = 4 \end{array}\right. \).
- إجابة
-
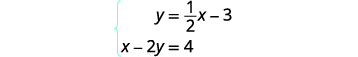
لرسم المعادلة الأولى بيانيًا، سنستخدم
منحدرها والجزء المقطوع من y.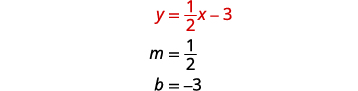
لرسم المعادلة الثانية بيانيًا، سنستخدم
القطع المقطوعة.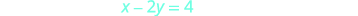
رسم الخطوط بيانيًا. 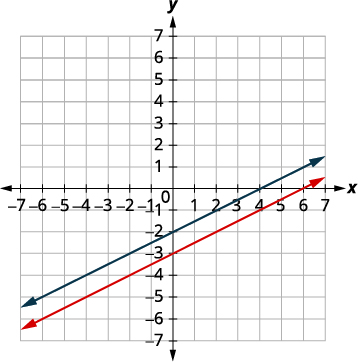
حدد نقاط التقاطع. الخطوط متوازية.
نظرًا لعدم وجود نقطة في كلا الخطين، لا يوجد زوج
مرتب يجعل كلا المعادلتين
صحيحتين. لا يوجد حل لهذا النظام.
حل النظام عن طريق الرسم البياني:\(\left\{ \begin{array} {l} y = -\tfrac{1}{4}x+2 \\ x+4y = 4 \end{array}\right. \).
- إجابة
-
لا يوجد حل
حل النظام عن طريق الرسم البياني:\(\left\{ \begin{array} {l} y = 3x-1 \\ 6x-2y = 6 \end{array}\right. \).
- إجابة
-
لا يوجد حل
في بعض الأحيان تمثل المعادلات في النظام نفس الخط. نظرًا لأن كل نقطة على الخط تجعل المعادلتين صحيحتين، فهناك عدد لا نهائي من الأزواج المرتبة التي تجعل كلتا المعادلتين صحيحتين. هناك العديد من الحلول التي لا حصر لها للنظام.
حل النظام عن طريق الرسم البياني:\(\left\{ \begin{array} {l} y = 2x-3 \\ -6x+3y = 9 \end{array}\right. \).
- إجابة
-
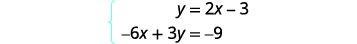
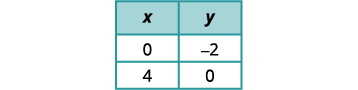
أوجد ميل المعادلة الأولى وقطعها الصادي. 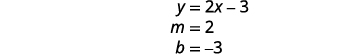
أوجد الأجزاء المقطوعة للمعادلة الثانية. 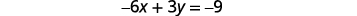
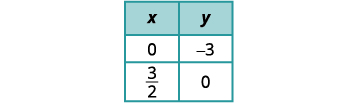
رسم الخطوط بيانيًا. 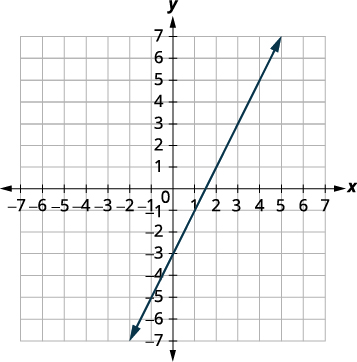
الخطوط هي نفسها!
نظرًا لأن كل نقطة على الخط تجعل
المعادلتين صحيحتين، فهناك عدد لا نهائي من الأزواج
المرتبة التي تجعل كلتا المعادلتين صحيحتين.
هناك العديد من الحلول لهذا النظام.إذا كتبت المعادلة الثانية في صورة تقاطع منحدر، فقد تدرك أن المعادلات لها نفس الميل ونفس التقاطع y.
حل النظام عن طريق الرسم البياني:\(\left\{ \begin{array} {l} y = -3x-6 \\ 6x+2y = -12 \end{array}\right. \).
- إجابة
-
العديد من الحلول بلا حدود
حل النظام عن طريق الرسم البياني:\(\left\{ \begin{array} {l} y = \tfrac{1}{2}x-4 \\ 2x-4y = 16 \end{array}\right. \).
- إجابة
-
العديد من الحلول بلا حدود
عندما قمنا برسم السطر الثاني في المثال الأخير، قمنا برسمه مباشرة فوق السطر الأول. نقول أن الخطين متزامنان. الخطوط المتزامنة لها نفس المنحدر ونفس التقاطع y.
الخطوط المتزامنة لها نفس المنحدر ونفس التقاطع y.
يحتوي كل من أنظمة المعادلات في المثال والمثال على خطين متقاطعين. كان لكل نظام حل واحد.
على سبيل المثال، أعطت المعادلات خطوطًا متزامنة، وبالتالي كان لدى النظام العديد من الحلول بلا حدود.
كان للأنظمة في هذه الأمثلة الثلاثة حل واحد على الأقل. يُطلق على نظام المعادلات الذي يحتوي على حل واحد على الأقل اسم النظام المتسق.
النظام ذو الخطوط المتوازية، مثل المثال، ليس له حل. نسمي نظامًا من المعادلات مثل هذا غير متناسق. ليس لديها حل.
نظام المعادلات المتسق هو نظام معادلات بحل واحد على الأقل.
نظام المعادلات غير المتسق هو نظام معادلات بدون حل.
نقوم أيضًا بتصنيف المعادلات في نظام المعادلات عن طريق تسمية المعادلات بأنها مستقلة أو تابعة. إذا كانت هناك معادلتين مستقلتين، فلكل منهما مجموعة الحلول الخاصة بها. الخطوط المتقاطعة والخطوط المتوازية مستقلة.
في حالة اعتماد معادلتين، فإن جميع حلول المعادلة الواحدة هي أيضًا حلول للمعادلة الأخرى. عندما نرسم معادلتين تابعتين، نحصل على خطوط متزامنة.
دعونا نلخص ذلك من خلال النظر إلى الرسوم البيانية للأنواع الثلاثة من الأنظمة. انظر أدناه والجدول.
| خطوط | متقاطعة | الموازي | صدفة |
|---|---|---|---|
| عدد الحلول | نقطة واحدة | لا يوجد حل | عدد لا نهائي |
| ثابت/غير متناسق | متسق | غير متناسقة | متسق |
| معالة/مستقلة | مستقل | مستقل | تابع |
بدون رسم بياني، حدد عدد الحلول ثم صنف نظام المعادلات.
ⓐ\( \left\{ \begin{array} {l} y = 3x−1 \\ 6x−2y = 12 \end{array}\right. \) ⓑ\( \left\{ \begin{array} {l} 2x+y=−3 \\ x−5y=5 \end{array} \right. \)
- إجابة
-
ⓐ سنقارن منحدرات واعتراض الخطين.
\(\begin{array} {lll} {} &{} &{ \left\{ \begin{array} {l} {y=3x-1} \\ {6x−2y=12} \end{array} \right. } \\ {} &{} &{y = 3x-1} \\ {\text{The first equation is already in slope-intercept form.}} &{} &{} \\ {\text{Write the second equation in slope-intercept form.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{6x-2y=12} \\ {} &{} &{-2y=-6x+12} \\ {} &{} &{\frac{-2y}{-2}=\frac{-6x+12}{-2}} \\ {} &{} &{y=3x-6} \\ {} &{y=3x-1} &{y=3x-6} \\ {} &{m=3} &{m=3} \\ {} &{b=-1} &{b=-6} \\ {\text{Find the slope and intercept of each line.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{\text{Since the slopes are the same andy-intercepts are}} &{} \\ {} &{\text{different, the lines are parallel.}} &{} \\ \end{array}\)
ⓑ سنقارن انحدار واعتراض الخطين.
\(\begin{array} {lll} {} &{} &{} \\ {} &{ \left\{ \begin{array} {l} 2x+y=-3 \\ x-5y=5 \\ \end{array} \right. } &{} \\ {\text{Write both equations in slope–intercept form.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{2x+y=-3} &{x-5y=5} \\ {} &{y=-2x-3} &{-5y=-x+5} \\ {} &{} &{\frac{-5y}{-5}=\frac{-x+5}{-5}} \\ {} &{} &{y=\frac{1}{5}-1} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {\text{Find the slope and intercept of each line.}} &{} &{} \\ {} &{} &{} \\ {} &{y=-2x-3} &{y=\frac{1}{5}-1} \\ {} &{m=-2} &{m=\frac{1}{5}} \\ {} &{b=-3} &{b=-1} \\ {} &{} &{} \\ {} &{\text{Since the slopes are different, the lines intersect.}} &{} \\ \end{array}\)
يحتوي نظام المعادلات التي تتقاطع رسوماتها البيانية على حل واحد وهو ثابت ومستقل.
بدون رسم بياني، حدد عدد الحلول ثم صنف نظام المعادلات.
ⓐ\(\left\{ \begin{array} {l} y=−2x−4 \\ 4x+2y=9 \end{array} \right. \) ⓑ\(\left\{ \begin{array} {l} 3x+2y=2 \\ 2x+y=1 \end{array} \right. \)
- إجابة
-
ⓐ لا يوجد حل، غير متناسق، مستقل ⓑ حل واحد، متسق، مستقل
بدون رسم بياني، حدد عدد الحلول ثم صنف نظام المعادلات.
ⓐ\(\left\{ \begin{array} {l} y=\frac{1}{3}x−5 \\ x−3y=6 \end{array} \right. \) ⓑ\(\left\{ \begin{array} {l} x+4y=12 \\ −x+y=3 \end{array} \right. \)
- إجابة
-
ⓐ لا يوجد حل، غير متناسق، مستقل ⓑ حل واحد، متسق، مستقل
يعد حل أنظمة المعادلات الخطية بالرسوم البيانية طريقة جيدة لتصور أنواع الحلول التي قد تنتج. ومع ذلك، هناك العديد من الحالات التي يكون فيها حل النظام عن طريق الرسوم البيانية غير مريح أو غير دقيق. إذا كانت الرسوم البيانية تمتد خارج الشبكة الصغيرة مع x و y بين\(−10\) 0 و 10، فقد يكون رسم الخطوط مرهقًا. وإذا لم تكن حلول النظام عبارة عن أعداد صحيحة، فقد يكون من الصعب قراءة قيمها بدقة من الرسم البياني.
حل نظام المعادلات بالتعويض
سنحل الآن أنظمة المعادلات الخطية بطريقة الاستبدال.
سنستخدم نفس النظام الذي استخدمناه أولاً للرسم البياني.
\[ \left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \nonumber \]
سنحل أولاً إحدى المعادلات الخاصة بـ x أو y. يمكننا اختيار أي من المعادلتين وحل أي من المتغيرين - لكننا سنحاول اتخاذ خيار من شأنه أن يجعل العمل سهلاً.
ثم نستبدل هذا التعبير بالمعادلة الأخرى. والنتيجة هي معادلة بمتغير واحد فقط - ونحن نعرف كيفية حلها!
بعد العثور على قيمة متغير واحد، سنقوم باستبدال هذه القيمة بإحدى المعادلات الأصلية وحل المتغير الآخر. أخيرًا، نتحقق من حلنا ونتأكد من صحة المعادلتين.
حل النظام عن طريق الاستبدال:\( \left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \)
- إجابة
-






حل النظام عن طريق الاستبدال:\( \left\{ \begin{array} {l} −2x+y=−11 \\ x+3y=9 \end{array} \right. \)
- إجابة
-
\((6,1)\)
حل النظام عن طريق الاستبدال:\( \left\{ \begin{array} {l} 2x+y=−1 \\ 4x+3y=3 \end{array} \right. \)
- إجابة
-
\((−3,5)\)
- حل إحدى المعادلات لأي متغير.
- استبدل التعبير من الخطوة 1 بالمعادلة الأخرى.
- حل المعادلة الناتجة.
- استبدل الحل في الخطوة 3 بأي من المعادلات الأصلية للعثور على المتغير الآخر.
- اكتب الحل كزوج مطلوب.
- تأكد من أن الزوج المطلوب هو حل لكل من المعادلتين الأصليتين.
كن حذرًا جدًا مع العلامات الموجودة في المثال التالي.
حل النظام عن طريق الاستبدال:\( \left\{ \begin{array} {l} 4x+2y=4 \\ 6x−y=8 \end{array} \right. \)
- إجابة
-
نحن بحاجة إلى حل معادلة واحدة لمتغير واحد. سنحل المعادلة الأولى لـ y.
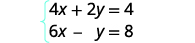
حل المعادلة الأولى لـ y.
استبدل\(−2x+2\) y في المعادلة الثانية.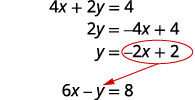
استبدل y بـ\(−2x+2\). 
حل المعادلة لـ x. 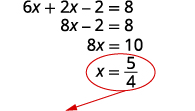
استبدل\(x=54\) البحث\(4x+2y=4\) للعثور على y. 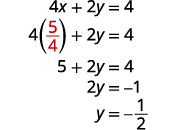
الزوج المطلوب هو\((54,−12)\). تحقق من الزوج المرتب في كلتا المعادلتين.
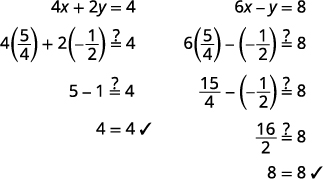
الحل هو\((54,−12)\).
حل النظام عن طريق الاستبدال:\( \left\{ \begin{array} {l} x−4y=−4 \\ −3x+4y=0 \end{array} \right. \)
- إجابة
-
\((2,32)\)
حل النظام عن طريق الاستبدال:\( \left\{ \begin{array} {l} 4x−y=0 \\ 2x−3y=5 \end{array} \right. \)
- إجابة
-
\((−12,−2)\)
حل نظام المعادلات بالحذف
لقد قمنا بحل أنظمة المعادلات الخطية عن طريق الرسوم البيانية والاستبدال. يعمل الرسم البياني جيدًا عندما تكون المعاملات المتغيرة صغيرة ويكون للحل قيم عددية. يعمل الاستبدال جيدًا عندما نتمكن بسهولة من حل معادلة واحدة لأحد المتغيرات وعدم وجود عدد كبير جدًا من الكسور في التعبير الناتج.
الطريقة الثالثة لحل أنظمة المعادلات الخطية تسمى طريقة الحذف. عندما حللنا نظامًا عن طريق الاستبدال، بدأنا بمعادلتين ومتغيرين وخفضناه إلى معادلة واحدة بمتغير واحد. هذا ما سنفعله مع طريقة الإزالة أيضًا، ولكن سيكون لدينا طريقة مختلفة للوصول إلى هناك.
تعتمد طريقة الحذف على خاصية إضافة المساواة. تقول خاصية الجمع للمساواة أنه عندما تضيف نفس الكمية إلى كلا طرفي المعادلة، تظل لديك المساواة. سنقوم بتوسيع خاصية إضافة المساواة لنقول أنه عند إضافة كميات متساوية لكلا طرفي المعادلة، تكون النتائج متساوية.
لأي تعبيرات أ، ب، ج، د.
\[\begin{array} {ll} {\text{if}} &{a=b} \\ {\text{and}} &{c=d} \\ {\text{then}} &{a+c=b+d.} \\ \nonumber \end{array}\]
لحل نظام المعادلات بالحذف، نبدأ بكلتا المعادلتين في الشكل القياسي. ثم نقرر أي متغير سيكون من الأسهل إزالته. كيف نقرر؟ نريد أن تكون معاملات متغير واحد أضداد، حتى نتمكن من جمع المعادلات معًا وإزالة هذا المتغير.
لاحظ كيف يعمل ذلك عندما نجمع هاتين المعادلتين معًا:
\[\left\{ \begin{array} {l} 3x+y=5 \\ \underline{2x−y=0} \end{array} \right. \nonumber\]
\[5x=5 \nonumber\]
يتم إضافة y إلى الصفر ولدينا معادلة واحدة بمتغير واحد.
دعونا نجرب واحدة أخرى:
\[ \left\{ \begin{array} x+4y=2 \\ 2x+5y=−2 \end{array} \right. \nonumber\]
هذه المرة لا نرى متغيرًا يمكن حذفه فورًا إذا أضفنا المعادلات.
ولكن إذا ضربنا المعادلة الأولى في\(−2\)، سنقوم بعمل معاملات x الأضداد. يجب أن نضرب كل حد على جانبي المعادلة في\(−2\).
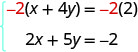
ثم أعد كتابة نظام المعادلات.
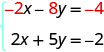
نرى الآن أن معاملات مصطلحات x هي أضداد، لذلك سيتم حذف x عندما نضيف هاتين المعادلتين.
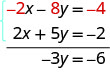
بمجرد أن نحصل على معادلة بمتغير واحد فقط، نقوم بحلها. ثم نستبدل هذه القيمة بإحدى المعادلات الأصلية لحلها للمتغير المتبقي. وكما هو الحال دائمًا، نتحقق من إجابتنا للتأكد من أنها حل لكل من المعادلتين الأصليتين.
سنرى الآن كيفية استخدام الحذف لحل نفس نظام المعادلات الذي قمنا بحله عن طريق التمثيل البياني والاستبدال.
حل النظام عن طريق الإزالة:\(\left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \)
- إجابة
-






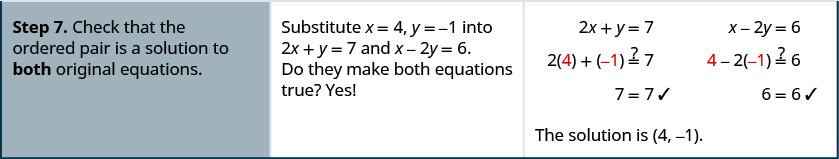
حل النظام عن طريق الإزالة:\(\left\{ \begin{array} {l} 3x+y=5 \\ 2x−3y=7 \end{array} \right.\)
- إجابة
-
\((2,−1)\)
حل النظام عن طريق الإزالة:\(\left\{ \begin{array} {l} 4x+y=−5 \\ −2x−2y=−2 \end{array} \right.\)
- إجابة
-
\((−2,3)\)
يتم سرد الخطوات هنا لسهولة الرجوع إليها.
- اكتب المعادلتين في الصورة القياسية. إذا كانت أي معاملات عبارة عن كسور، فقم بإزالتها.
- قم بعمل معاملات أضداد متغير واحد.
- حدد المتغير الذي ستقوم بإزالته.
- اضرب معادلتين أو كلتيهما بحيث تكون معاملات هذا المتغير أضداد.
- أضف المعادلات الناتجة من الخطوة 2 لإزالة متغير واحد.
- حل للمتغير المتبقي.
- استبدل الحل من الخطوة 4 بإحدى المعادلات الأصلية. ثم قم بحل المتغير الآخر.
- اكتب الحل كزوج مطلوب.
- تأكد من أن الزوج المطلوب هو حل لكل من المعادلتين الأصليتين.
الآن سنقوم بعمل مثال حيث نحتاج إلى ضرب كلتا المعادلتين بالثوابت من أجل جعل معاملات أضداد متغير واحد.
حل النظام عن طريق الإزالة:\(\left\{ \begin{array} {l} 4x−3y=9 \\ 7x+2y=−6 \end{array} \right. \)
- إجابة
-
في هذا المثال، لا يمكننا ضرب معادلة واحدة فقط بأي ثابت للحصول على معاملات عكسية. لذلك سنضرب كلا المعادلتين بشكل استراتيجي بثوابت مختلفة للحصول على الأضداد.
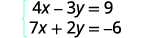
كلا المعادلتين في الشكل القياسي.
للحصول على معاملات عكسية لـ y،
سنضرب المعادلة الأولى في 2 والمعادلة
الثانية في 3.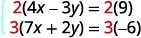
قم بالتبسيط. 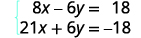
أضف المعادلتين لإزالة y. 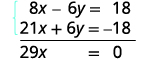
حل لـ x. 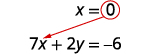
استبدل x=0x=0 بإحدى المعادلات الأصلية. 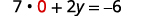
حل من أجلك. 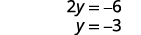
اكتب الحل كزوج مطلوب. الزوج المطلوب هو\((0,−3)\).
تأكد من أن الزوج المطلوب هو حل
لكل من المعادلتين الأصليتين.
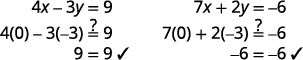
الحل هو\((0,−3)\).
حل النظام عن طريق الإزالة:\(\left\{ \begin{array} {l} 3x−4y=−9 \\ 5x+3y=14\end{array} \right. \)
- إجابة
-
\((1,3)\)
حل كل نظام عن طريق الإزالة:\(\left\{ \begin{array} {l} 7x+8y=4 \\ 3x−5y=27 \end{array} \right.\)
- إجابة
-
\((4,−3)\)
عندما يحتوي نظام المعادلات على كسور، سنقوم أولاً بمسح الكسور بضرب كل معادلة في شاشة LCD لجميع الكسور في المعادلة.
حل النظام عن طريق الإزالة:\(\left\{ \begin{array} {l} x+\tfrac{1}{2}y=6 \\ \tfrac{3}{2}x+\tfrac{2}{3}y=\tfrac{17}{2} \end{array} \right.\)
- إجابة
-
في هذا المثال، تحتوي كلتا المعادلتين على كسور. ستكون خطوتنا الأولى هي ضرب كل معادلة في شاشة LCD لجميع الكسور في المعادلة لمسح الكسور.
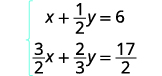
لمسح الكسور، اضرب كل
معادلة في شاشة LCD الخاصة بها.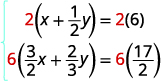
قم بالتبسيط. 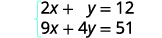
الآن نحن على استعداد للقضاء على
أحد المتغيرات. لاحظ أن كلا المعادلتين في الشكل
القياسي.يمكننا إزالة y بضرب المعادلة العليا في\(−4\). 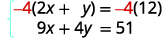
قم بالتبسيط والإضافة.
\(x=3\)استبدل بإحدى المعادلات الأصلية.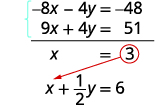
حل من أجلك. 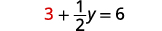
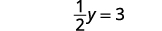
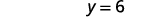
اكتب الحل كزوج مطلوب. الزوج المطلوب هو\((3,6)\). تأكد من أن الزوج المطلوب هو حل
لكل من المعادلتين الأصليتين.

الحل هو\((3,6)\).
حل كل نظام عن طريق الإزالة:\(\left\{ \begin{array} {l} \tfrac{1}{3}x−\tfrac{1}{2}y=1 \\ \tfrac{3}{4}x−y=\tfrac{5}{2} \end{array} \right.\)
- إجابة
-
\((6,2)\)
حل كل نظام عن طريق الإزالة:\(\left\{ \begin{array} {l} x+\tfrac{3}{5}y=−\tfrac{1}{5} \\ −\tfrac{1}{2}x−\tfrac{2}{3}y=\tfrac{5}{6} \end{array} \right.\)
- إجابة
-
\((1,−2)\)
عندما قمنا بحل النظام بالرسم البياني، رأينا أنه لا تحتوي جميع أنظمة المعادلات الخطية على زوج واحد مرتب كحل. عندما كانت المعادلتين في الواقع نفس الخط، كان هناك عدد لا نهائي من الحلول. أطلقنا على ذلك نظامًا ثابتًا. عندما وصفت المعادلتين الخطوط المتوازية، لم يكن هناك حل. أطلقنا على ذلك نظامًا غير متناسق.
وينطبق الشيء نفسه باستخدام الاستبدال أو الإزالة. إذا كانت المعادلة في نهاية الاستبدال أو الحذف عبارة صحيحة، فلدينا نظام ثابت ولكنه تابع ونظام المعادلات يحتوي على العديد من الحلول بلا حدود. إذا كانت المعادلة في نهاية الاستبدال أو الحذف عبارة خاطئة، فلدينا نظام غير متناسق ونظام المعادلات ليس له حل.
حل النظام عن طريق الإزالة:\(\left\{ \begin{array} {l} 3x+4y=12 \\ y=3−\tfrac{3}{4}x \end{array} \right. \)
- إجابة
-
\(\begin{array} {ll} {} &{ \left\{ \begin{array} {l} 3x+4y=12 \\ y=3−\frac{3}{4}x \end{array} \right.} \\ {} &{} \\ {\text{Write the second equation in standard form.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ \frac{3}{4}x+y=3 \end{array} \right. } \\ {} &{} \\ {\text{Clear the fractions by multiplying the } \\ \text{second equation by 4.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ 4(\frac{3}{4}x+y)=4(3) \end{array} \right. } \\ {} &{} \\ {\text{Simplify.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ 3x+4y=12 \end{array} \right. } \\ {} &{} \\ {\text{To eliminate a variable, we multiply the} \\ \text{second equation by−1. Simplify and add.}} &{\begin{array} {l} {\left\{ \begin{array} {l} 3x+4y=12 \\ \underline{-3x-4y=-12 } \end{array} \right.} \\ {\hspace{16mm} 0=0} \end{array}} \\ \end{array} \)
هذا بيان حقيقي. المعادلات متسقة ولكنها تعتمد. ستكون الرسوم البيانية الخاصة بهم هي نفس السطر. يحتوي النظام على العديد من الحلول بلا حدود.
بعد مسح الكسور في المعادلة الثانية، هل لاحظت أن المعادلتين متماثلتان؟ هذا يعني أن لدينا خطوطًا متزامنة.
حل النظام عن طريق الإزالة:\(\left\{ \begin{array} {l} 5x−3y=15 \\ 5y=−5+\tfrac{5}{3}x \end{array} \right. \)
- إجابة
-
العديد من الحلول بلا حدود
حل النظام عن طريق الإزالة:\(\left\{ \begin{array} {l} x+2y=6 \\ y=−\tfrac{1}{2}x+3\end{array} \right. \)
- إجابة
-
العديد من الحلول بلا حدود
اختر الطريقة الأكثر ملاءمة لحل نظام المعادلات الخطية
عندما تقوم بحل نظام المعادلات الخطية في أحد التطبيقات، لن يتم إخبارك بالطريقة التي يجب استخدامها. سوف تحتاج إلى اتخاذ هذا القرار بنفسك. لذلك ستحتاج إلى اختيار الطريقة الأسهل للقيام بها وتقليل فرصتك في ارتكاب الأخطاء.
\[ \textbf{Choose the Most Convenient Method to Solve a System of Linear Equations} \\ \begin{array} {lll} {\underline{\textbf{Graphing}}} &{\underline{\textbf{Substitution}}} &{\underline{\textbf{Elimination}}} \\ {\text{Use when you need a}} &{\text{Use when one equation is}} &{\text{Use when the equations a}} \\ {\text{picture of the situation.}} &{\text{already solved or can be}} &{\text{rein standard form.}} \\ {\text{}} &{\text{easily solved for one}} &{\text{}} \\ {\text{}} &{\text{variable.}} &{\text{}} \\ \end{array} \nonumber \]
بالنسبة لكل نظام من المعادلات الخطية، حدد ما إذا كان من الأنسب حلها عن طريق الاستبدال أو الحذف. اشرح إجابتك.
ⓐ\(\left\{ \begin{array} {l} 3x+8y=40 \\ 7x−4y=−32 \end{array} \right.\) ⓑ\(\left\{ \begin{array} {l} 5x+6y=12 \\ y=\tfrac{2}{3}x−1 \end{array} \right.\)
- إجابة
-
ⓐ
\[\left\{ \begin{array} {l} 3x+8y=40 \\ 7x−4y=−32 \end{array} \right.\nonumber\]
نظرًا لأن كلتا المعادلتين في الشكل القياسي، فإن استخدام الحذف سيكون أكثر ملاءمة.
ⓑ
\[\left\{ \begin{array} {l} 5x+6y=12 \\ y=\tfrac{2}{3}x−1 \end{array} \right.\nonumber \]
نظرًا لأن معادلة واحدة قد تم حلها بالفعل لـ y، فإن استخدام الاستبدال سيكون أكثر ملاءمة.
بالنسبة لكل نظام من المعادلات الخطية، حدد ما إذا كان من الأنسب حلها عن طريق الاستبدال أو الحذف. اشرح إجابتك.
ⓐ\(\left\{ \begin{array} {l} 4x−5y=−32 \\ 3x+2y=−1 \end{array} \right.\) ⓑ\(\left\{ \begin{array} {l} x=2y−1 \\ 3x−5y=−7 \end{array} \right.\)
- إجابة
-
ⓐ نظرًا لأن كلتا المعادلتين في الشكل القياسي، فسيكون استخدام الحذف أكثر ملاءمة. ⓑ نظرًا لأن معادلة واحدة قد تم حلها بالفعل لـ x، فإن استخدام الاستبدال سيكون أكثر ملاءمة.
بالنسبة لكل نظام من المعادلات الخطية، حدد ما إذا كان من الأنسب حلها عن طريق الاستبدال أو الحذف. اشرح إجابتك.
ⓐ\(\left\{ \begin{array} {l} y=2x−1 \\ 3x−4y=−6 \end{array} \right.\) ⓑ\(\left\{ \begin{array} {l} 6x−2y=12 \\ 3x+7y=−13 \end{array} \right.\)
- إجابة
-
ⓐ نظرًا لأن معادلة واحدة قد تم حلها بالفعل لـ y، فإن استخدام الاستبدال سيكون أكثر ملاءمة. ⓑ نظرًا لأن كلتا المعادلتين في الشكل القياسي، فإن استخدام الحذف سيكون أكثر ملاءمة.
المفاهيم الرئيسية
- كيفية حل نظام المعادلات الخطية بالرسم البياني.
- ارسم المعادلة الأولى بيانيًا.
- ارسم المعادلة الثانية على نفس نظام الإحداثيات المستطيلة.
- حدد ما إذا كانت الخطوط تتقاطع أو متوازية أو هي نفس الخط.
- حدد الحل للنظام.
في حالة تقاطع الخطوط، حدد نقطة التقاطع. هذا هو الحل للنظام.
إذا كانت الخطوط متوازية، فلن يكون لدى النظام أي حل.
إذا كانت الخطوط هي نفسها، فإن النظام يحتوي على عدد لا نهائي من الحلول. - تحقق من الحل في كلتا المعادلتين.
- كيفية حل نظام المعادلات عن طريق الاستبدال.
- حل إحدى المعادلات لأي متغير.
- استبدل التعبير من الخطوة 1 بالمعادلة الأخرى.
- حل المعادلة الناتجة.
- استبدل الحل في الخطوة 3 بأي من المعادلات الأصلية للعثور على المتغير الآخر.
- اكتب الحل كزوج مطلوب.
- تأكد من أن الزوج المطلوب هو حل لكل من المعادلتين الأصليتين.
- كيفية حل نظام المعادلات بالحذف.
- اكتب المعادلتين في الصورة القياسية. إذا كانت أي معاملات عبارة عن كسور، فقم بإزالتها.
- قم بعمل معاملات أضداد متغير واحد.
حدد المتغير الذي ستقوم بإزالته.
اضرب معادلتين أو كلتيهما بحيث تكون معاملات هذا المتغير أضداد. - أضف المعادلات الناتجة من الخطوة 2 لإزالة متغير واحد.
- حل للمتغير المتبقي.
- استبدل الحل من الخطوة 4 بإحدى المعادلات الأصلية. ثم قم بحل المتغير الآخر.
- اكتب الحل كزوج مطلوب.
- تأكد من أن الزوج المطلوب هو حل لكل من المعادلتين الأصليتين. \[ \textbf{Choose the Most Convenient Method to Solve a System of Linear Equations} \\ \begin{array} {lll} {\underline{\textbf{Graphing}}} &{\underline{\textbf{Substitution}}} &{\underline{\textbf{Elimination}}} \\ {\text{}} &{\text{Use when one equation is}} &{\text{}} \\ {\text{Use when you need a}} &{\text{already solved or can be}} &{\text{Use when the equations a}} \\ {\text{picture of the situation.}} &{\text{easily solved for one}} &{\text{rein standard form.}} \\ {\text{}} &{\text{variable.}} &{\text{}} \\ \end{array} \nonumber \]
مسرد المصطلحات
- خطوط متزامنة
- الخطوط المتزامنة لها نفس المنحدر ونفس التقاطع y.
- أنظمة متسقة وغير متسقة
- نظام المعادلات المتسق هو نظام معادلات بحل واحد على الأقل؛ نظام المعادلات غير المتسق هو نظام معادلات بدون حل.
- حلول نظام المعادلات
- حلول نظام المعادلات هي قيم المتغيرات التي تجعل جميع المعادلات صحيحة؛ يتم تمثيل الحل بزوج مرتب (x، y). (س، ص).
- نظام المعادلات الخطية
- عندما يتم تجميع معادلتين خطيتين أو أكثر معًا، فإنها تشكل نظامًا من المعادلات الخطية.