1.5: الأعداد العشرية
- Page ID
- 201574
في نهاية هذا القسم، ستكون قادرًا على:
- الأرقام العشرية المستديرة
- جمع الأعداد العشرية وطرحها
- ضرب الأرقام العشرية وقسمتها
- تحويل الأعداد العشرية والكسور والنسب المئوية
- تبسيط التعبيرات باستخدام الجذور التربيعية
- حدد الأعداد الصحيحة والأرقام العقلانية والأرقام غير المنطقية والأرقام الحقيقية
- حدد موقع الكسور والأعداد العشرية على خط الأعداد
يمكن العثور على مقدمة أكثر شمولاً للموضوعات التي يتم تناولها في هذا القسم في فصل الجبر الأولي، الأسس.
الأعداد العشرية المستديرة
الأعداد العشرية هي طريقة أخرى لكتابة الكسور التي مقاماتها هي قوى العشرة.
\[\begin{array}{rcll} 0.1 & = & \dfrac{1}{10} & \text{is “one tenth”} \\ 0.01 & = & \dfrac{1}{100} & \text{is “one hundredth”} \\ 0.001 & = & \dfrac{1}{1000} & \text{is “one thousandth”} \\ 0.0001 & = & \dfrac{1}{10,000} & \text{is “one ten-thousandth”} \end{array}\]
كما هو الحال في الأعداد الصحيحة، فإن كل رقم من الأرقام العشرية يتوافق مع القيمة المكانية بناءً على قوى العشرة. يعرض الشكل أسماء القيم المكانية على يسار ويمين العلامة العشرية.
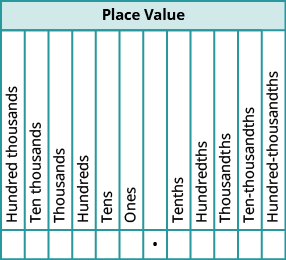
عندما نتعامل مع الأرقام العشرية، غالبًا ما يكون من الضروري تقريب الرقم إلى أقرب قيمة مكانية مطلوبة. نلخص خطوات تقريب الرقم العشري هنا.
- حدد القيمة المكانية المحددة وقم بتمييزها بسهم.
- ضع خط تحت الرقم الموجود على يمين القيمة المكانية.
- هل الرقم المسطر أكبر من أو يساوي 5؟
- نعم: أضف 1 إلى الرقم في القيمة المكانية المحددة.
- لا: لا تقم بتغيير الرقم في القيمة المكانية المحددة
- أعد كتابة الرقم، مع حذف جميع الأرقام الموجودة على يمين رقم التقريب.
\(18.379\)قرِّب العدد الصحيح لأقرب ⓐ جزء من مائة ⓑ العاشر ⓒ.
- إجابة
-
مستدير\(18.379.\)
ⓐ إلى أقرب جزء من مائة
حدد موقع المكان من مائة بسهم. 
ضع خط تحت الرقم الموجود على يمين القيمة المكانية المحددة. 
ولأن 9 أكبر من أو يساوي 5، أضف 1 إلى 7. 
أعد كتابة الرقم، مع حذف جميع الأرقام الموجودة على يمين رقم التقريب. 
لاحظ أن الأرقام المحذوفة لم يتم استبدالها بالأصفار. 
ⓑ إلى أقرب جزء من عشرة
حدد موقع المكان العاشر بسهم. 
ضع خط تحت الرقم الموجود على يمين القيمة المكانية المحددة. 
ولأن 7 أكبر من أو يساوي 5، أضف 1 إلى 3. 
أعد كتابة الرقم، مع حذف جميع الأرقام الموجودة على يمين رقم التقريب. 
لاحظ أن الأرقام المحذوفة لم يتم استبدالها بالأصفار. 
ⓒ إلى أقرب رقم صحيح
حدد مكان تلك باستخدام سهم. 
ضع خط تحت الرقم الموجود على يمين القيمة المكانية المحددة. 
نظرًا لأن 3 لا يزيد عن أو يساوي 5، فلا تضيف 1 إلى 8. 
أعد كتابة الرقم، مع حذف جميع الأرقام الموجودة على يمين رقم التقريب. 

\(6.582\)قرِّب العدد الصحيح لأقرب ⓐ جزء من مائة ⓑ العاشر ⓒ.
- إجابة
-
ⓐ\(6.58\) ⓑ\(6.6\) ⓒ\(7\)
قرِّب\(15.2175\) إلى أقرب ⓐ جزء من ألف ⓑ جزء من مائة ⓒ إلى الجزء العاشر.
- إجابة
-
ⓐ\(15.218\) ⓑ\(15.22\)
ⓒ\(15.2\)
جمع الأعداد العشرية وطرحها
لجمع أو طرح الكسور العشرية، نقوم بمحاذاة النقاط العشرية. من خلال ترتيب النقاط العشرية بهذه الطريقة، يمكننا إضافة أو طرح قيم المكان المقابلة. ثم نقوم بعد ذلك بإضافة الأرقام أو طرحها كما لو كانت أعدادًا صحيحة ثم نضع الفاصلة العشرية في المجموع.
- حدد علامة المجموع أو الفرق.
- اكتب الأرقام بحيث تصطف النقاط العشرية رأسيًا.
- استخدم الأصفار كعناصر نائبة، حسب الحاجة.
- قم بإضافة الأرقام أو طرحها كما لو كانت أرقامًا صحيحة. ثم ضع النقطة
العشرية في الإجابة تحت النقاط العشرية في الأرقام المعطاة. - اكتب المجموع أو الفرق مع العلامة المناسبة.
إضافة أو طرح: ⓐ\(−23.5−41.38\) ⓑ\(14.65−20.\)
- إجابة
-
ⓐ
\(\begin{array}{ll} \text{} & −23.5−41.38 \\ \\ \\ {\text{The difference will be negative. To subtract, we add the} \\ \text{numerals. Write the numbers so the decimal points line} \\ \text{up vertically.}} & { \; \; 23.5 \\ \underline{+41.38}} \\ \\ \\ { \text{Put 0 as a placeholder after the 5 in 23.5.} \\ \text{Remember, } \frac{5}{10}=\frac{50}{100} \text{ so } 0.5=0.50.} & { \; \; 23.50 \\ \underline{+41.38}} \\ \\ \\ {\text{Add the numbers as if they were whole numbers.} \\ \text{Then place the decimal point in the sum.}} & {\; \; 23.50 \\ \underline{+41.38} \\ \; \; 64.88 } \\ \\ \\ \text{ Write the result with the correct sign.} & 64.88−23.5−41.38=−64.88 \end{array}\)
ⓑ
\(\begin{array}{ll} \text{} & 14.65−20 \\ \\ \\ {\text{The difference will be negative. To subtract, we} \\ \text{subtract 14.65 from 20.}} \\ \\ \\ {\text{Write the numbers so the decimal points line up} \\ \text{vertically.}} & { \; \; 20 \\ \underline{−14.65}} \\ \\ \\ {\text{Remember, 20 is a whole number, so place the} \\ \text{decimal point after the 0.}} \\ \\ \\ \text{Put in zeros to the right as placeholders.} & { \; \; 20.00 \\ \underline{−14.65}} \\ \\ \\ \text{Subtract and place the decimal point in the answer.} & {\begin{array}{lcccc} {} & 9 & {} & 9 & {} \\ 1 & \cancel{10} & {} & \cancel{10} & 10 \\ 2 & 0 & . & 0 & 0 \\ −1 & 4 & . & 6 & 5 \end{array} \\ \text{______________________} \\ \begin{array}{lcccc} {\; \; \; \; \; \; \; \; \; } & 5 & . & 3 & 5 \end{array}} \\ \\ \\ \text{Write the result with the correct sign.} & 14.65−20=−5.35 \end{array} \)
الجمع أو الطرح: ⓐ\(−4.8−11.69\) ⓑ\(9.58−10\).
- إجابة
-
ⓐ\(−16.49\) ⓑ\(−0.42\)
الجمع أو الطرح: ⓐ\(−5.123−18.47\) ⓑ\(37.42−50\).
- إجابة
-
ⓐ\(−23.593\) ⓑ\(−12.58\)
ضرب الأعداد العشرية وقسمتها
عندما نضرب الأعداد العشرية الموقعة، نحدد أولاً علامة المنتج ثم نضرب كما لو كان كلا الرقمين موجبين. نقوم بضرب الأرقام متجاهلين النقطة العشرية مؤقتًا ثم نحسب عدد النقاط العشرية في العوامل ويخبرنا هذا المجموع بعدد المنازل العشرية في المنتج. أخيرًا، نكتب المنتج بالعلامة المناسبة.
- حدد علامة المنتج.
- اكتب في شكل عمودي، واصطف الأرقام على اليمين. اضرب الأرقام كما لو كانت أرقامًا كاملة، مع تجاهل النقاط العشرية مؤقتًا.
- ضع النقطة العشرية. عدد المنازل العشرية في المنتج هو مجموع عدد
المنازل العشرية في العوامل. - اكتب المنتج بالعلامة المناسبة.
اضرب:\((−3.9)(4.075)\).
- إجابة
-
\((−3.9)(4.075)\) العلامات مختلفة.
سيكون المنتج سلبيًا.سيكون المنتج سلبيًا. اكتب في شكل عمودي، واصطف
الأرقام على اليمين.
اضرب. 
أضف عدد المنازل العشرية
في العوامل (1 + 3). ضع العلامة العشرية على بعد 4 أماكن من اليمين.

العلامات مختلفة، وبالتالي فإن المنتج سلبي. \((−3.9)(4.075)=−15.8925\)
اضرب:\(−4.5(6.107)\).
- إجابة
-
\(−27.4815\)
اضرب:\(−10.79(8.12)\).
- إجابة
-
\(−87.6148\)
في كثير من الأحيان، خاصة في العلوم، ستضرب الأعداد العشرية بقوى 10 (10، 100، 1000، إلخ). إذا قمت بضرب بعض المنتجات على الورق، فقد تلاحظ نمطًا يربط عدد الأصفار بقوة 10 بعدد المنازل العشرية، وننقل العلامة العشرية إلى اليمين للحصول على المنتج.
- انقل النقطة العشرية إلى اليمين بنفس عدد الأماكن مثل
عدد الأصفار بقوة 10. - أضف الأصفار في نهاية الرقم حسب الحاجة.
اضرب: 5.63 في ⓐ 10 ⓑ 100 ⓒ 1000.
- إجابة
-
بالنظر إلى عدد الأصفار في مضاعف العشرة، نرى عدد الأماكن التي نحتاج إليها لنقل العدد العشري إلى اليمين.
ⓐ
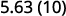
يوجد صفر واحد في 10، لذا انقل العلامة العشرية مكانًا واحدًا إلى اليمين. 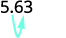
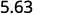
ⓑ
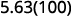
يوجد صفران في 100، لذا انقل العلامة العشرية مرتين إلى اليمين. 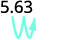

ⓒ
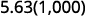
توجد ٣ أصفار في ١٠٠٠، لذا انقل العلامة العشرية رقم ٣ إلى اليمين. 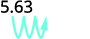
يجب إضافة صفر إلى النهاية. 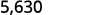
اضرب 2.58 في ⓐ 10 ⓑ 100 ⓒ 1000.
- إجابة
-
ⓐ 25.8 ⓑ 258 ⓒ 2,580
اضرب 14.2 في ⓐ 10 ⓑ 100 ⓒ 1000.
- إجابة
-
ⓐ 142 ⓑ 1,420 ⓒ 14,200
تمامًا كما هو الحال مع الضرب، فإن قسمة الأعداد العشرية الموقعة تشبه إلى حد كبير قسمة الأعداد الصحيحة. علينا فقط معرفة المكان الذي يجب وضع العلامة العشرية فيه وعلامة حاصل القسمة. عند قسمة الأعداد العشرية الموقعة، حدد أولاً علامة خارج القسمة ثم قسّم كما لو كان كلا الرقمين موجبين. أخيرًا، اكتب حاصل القسمة مع العلامة المناسبة.
نقوم بمراجعة الرموز والمفردات الخاصة بالقسمة:

سنكتب الخطوات التي يجب اتخاذها عند قسمة الأرقام العشرية لسهولة الرجوع إليها.
- حدد علامة حاصل القسمة.
- اجعل المقسوم رقمًا صحيحًا عن طريق «نقل» العلامة العشرية إلى اليمين. «انقل» النقطة العشرية في التوزيعات بنفس عدد المواضع - بإضافة الأصفار حسب الحاجة.
- يقسم. ضع النقطة العشرية في حاصل القسمة فوق النقطة العشرية في التوزيعات.
- اكتب حاصل القسمة مع العلامة المناسبة.
قسّم:\(−25.65÷(−0.06)\).
- إجابة
-
تذكر أنه يمكنك «نقل» الأعداد العشرية في المقسوم وتوزيع الأرباح بسبب خاصية الكسور المتكافئة.
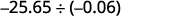
العلامات هي نفسها. حاصل القسمة إيجابي. اجعل المقسوم رقمًا صحيحًا عن طريق «نقل» العلامة العشرية إلى اليمين. «انقل» النقطة العشرية في التوزيعات بنفس عدد الأماكن. 
يقسم. ضع النقطة العشرية في حاصل القسمة فوق النقطة العشرية في التوزيعات. 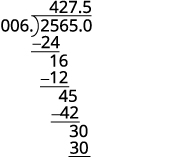
اكتب حاصل القسمة مع العلامة المناسبة. 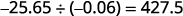
قسّم:\(−23.492÷(−0.04)\).
- إجابة
-
\(587.3\)
قسّم:\(−4.11÷(−0.12)\).
- إجابة
-
\(34.25\)
تحويل الأعداد العشرية والكسور والنسب المئوية
في عملنا، غالبًا ما يكون من الضروري تغيير شكل الرقم. قد نضطر إلى تغيير الكسور إلى أعداد عشرية أو الكسور العشرية إلى النسبة المئوية.
نقوم بتحويل الأعداد العشرية إلى كسور من خلال تحديد القيمة المكانية للرقم الأخير (أقصى اليمين). في العدد العشري 0.03. يكون الرقم 3 في خانة المئات، وبالتالي فإن 100 هو مقام الكسر المكافئ لـ 0.03.
\[0.03=\dfrac{3}{100}\]
يتم تلخيص الخطوات التي يجب اتخاذها لتحويل عدد عشري إلى كسر في مربع الإجراءات.
- لتحويل عدد عشري إلى كسر صحيح، حدد القيمة المكانية للرقم النهائي.
- اكتب الكسر.
- البسط - «الأرقام» الموجودة على يمين العلامة العشرية
- القاسم - القيمة المكانية المقابلة للرقم النهائي
- لتحويل كسر إلى رقم عشري، قسّم بسط الكسر على مقام الكسر.
اكتب: ⓐ\(0.374\) ككسر ⓑ\(−\frac{5}{8}\) في صورة عدد عشري.
- إجابة
-
ⓐ
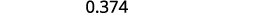
حدد القيمة المكانية للرقم النهائي. 
اكتب الكسر لـ 0.374: البسط هو 374. القاسم هو 1000. 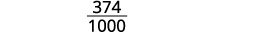
قم بتبسيط الكسر. 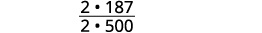
قسّم العوامل المشتركة. 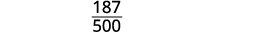
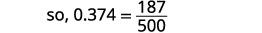
ⓑ نظرًا لأن شريط الكسر يعني القسمة، فإننا نبدأ بكتابة الكسر\(\frac{5}{8}\) كـ\(8\sqrt{5}\). الآن قسّم.
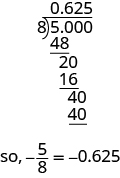
اكتب: ⓐ\(0.234\) ككسر ⓑ\(−\frac{7}{8}\) في صورة عدد عشري.
- إجابة
-
ⓐ\(\frac{117}{500}\) ⓑ\(−0.875\)
اكتب: ⓐ\(0.024\) ككسر ⓑ\(−\frac{3}{8}\) في صورة عدد عشري.
- إجابة
-
ⓐ\(\frac{3}{125}\) ⓑ\(−0.375\)
النسبة المئوية هي نسبة مقامها 100. النسبة المئوية تعني لكل مائة. نحن نستخدم رمز النسبة المئوية،%، لإظهار النسبة المئوية. نظرًا لأن النسبة المئوية هي نسبة، يمكن التعبير عنها بسهولة في صورة كسر. النسبة المئوية تعني لكل 100، وبالتالي فإن مقام الكسر هو 100. ثم نغير الكسر إلى رقم عشري بقسمة البسط على المقام. بعد القيام بذلك عدة مرات، قد ترى النمط.
لتحويل رقم النسبة المئوية إلى رقم عشري، ننقل العلامة العشرية مكانين إلى اليسار.
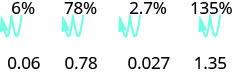
لتحويل عدد عشري إلى نسبة مئوية، تذكر أن النسبة المئوية تعني لكل مائة. إذا غيرنا العدد العشري إلى كسر مقامه 100، فمن السهل تغيير هذا الكسر إلى نسبة مئوية. بعد العديد من التحويلات، يمكنك التعرف على النمط.
لتحويل عدد عشري إلى نسبة مئوية، ننقل العلامة العشرية إلى منزلتين إلى اليمين ثم نضيف علامة النسبة المئوية.
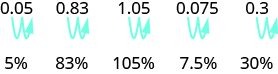
- لتحويل نسبة مئوية إلى عدد عشري، انقل العلامة العشرية إلى اليسار بعد إزالة علامة النسبة المئوية.
- لتحويل عدد عشري إلى نسبة مئوية، انقل العلامة العشرية منزلتين إلى اليمين ثم أضف علامة النسبة المئوية.
قم بتحويل كل منها:
ⓐ نسبة مئوية إلى عدد عشري: 62% و135% و13.7%.
ⓑ نسبة عشري إلى نسبة مئوية: 0.51 و1.25 و0.093.
- إجابة
-
ⓐ
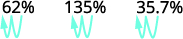
انقل العلامة العشرية مكانين إلى اليسار. 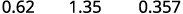
ⓑ
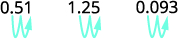
انقل العلامة العشرية مكانين إلى اليمين. 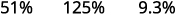
قم بتحويل كل منها:
ⓐ نسبة مئوية إلى عدد عشري: 9% و87% و3.9%.
ⓑ نسبة عشري إلى نسبة مئوية: 0.17 و1.75 و0.0825.
- إجابة
-
ⓐ 0.09، 0.87، 0.039 ⓑ 17٪، 175٪، 8.25٪
قم بتحويل كل منها:
ⓐ نسبة مئوية إلى عدد عشري: 3% و91% و8.3%.
ⓑ نسبة عشري إلى نسبة مئوية: 0.41 و2.25 و0.0925.
- إجابة
-
ⓐ 0.03، 0.91، 0.083 ⓑ 41٪، 225٪، 9.25٪
تبسيط التعبيرات باستخدام الجذور التربيعية
تذكر أنه عندما\(n\) يتم ضرب الرقم في حد ذاته، فإننا\(n^2\) نكتبه ونقرأه «\(n\)مربعًا». النتيجة تسمى مربع الرقم n. على سبيل المثال،\(\frac{8}{2}\) يُقرأ «8 مربع» ويسمى 64 مربع 8. وبالمثل، 121 هو مربع 11 لأنه\(11^2\) 121. سيكون من المفيد تعلم التعرف على الأرقام المربعة المثالية.
إذا كان\(n^2=m\) m هو مربع n.
ماذا عن مربعات الأرقام السالبة؟ نحن نعلم أنه عندما تكون علامات الرقمين متماثلة، يكون منتجهما إيجابيًا. لذا فإن مربع أي رقم سالب يكون موجبًا أيضًا.
\[(−3)^2=9 \; \; \; \; \; \; \; \; \; (−8)^2=64 \; \; \; \; \; \; \; \; \; (−11)^2=121 \; \; \; \; \; \; \; \; \; (−15)^2=225\]
لأننا\(10^2=100\) نقول أن 100 هو مربع 10. نقول أيضًا أن 10 هو الجذر التربيعي لـ 100. يُطلق على الرقم الذي مربعه m اسم الجذر التربيعي للرقم m.
إذا كان\(n^2=m\) n هو الجذر التربيعي لـ m.
لاحظ\((−10)^2=100\) أيضًا أن −10 يمثل أيضًا الجذر التربيعي لـ 100. لذلك، يمثل كل من 10 و−10 جذورًا مربعة لـ 100. لذلك، كل عدد موجب له جذران مربعان - أحدهما موجب والآخر سالب. تشير العلامة الراديكالية إلى الجذر التربيعي الإيجابي.\(\sqrt{m}\) يسمى الجذر التربيعي الموجب بالجذر التربيعي الرئيسي. عندما نستخدم العلامة الجذرية فهذا يعني دائمًا أننا نريد الجذر التربيعي الرئيسي.
\(\sqrt{m}\)تتم قراءة «الجذر التربيعي لـ mm».
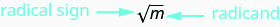
إذا\(m=n^2\)، إذن\(\sqrt{m}=n\)، من أجل\(n≥0\).
الجذر التربيعي لـ m،\(\sqrt{m}\)، هو الرقم الموجب الذي مربعه هو m.
نحن نعلم أن كل رقم موجب له جذران تربيعيان وأن العلامة الجذرية تشير إلى الموجب. نحن نكتب\(\sqrt{100}=10\). إذا أردنا إيجاد الجذر التربيعي السالب لعدد ما، فإننا نضع القيمة السالبة أمام العلامة الجذرية. على سبيل المثال،\(−\sqrt{100}=−10\). نقرأ على\(−\sqrt{100}\) أنه «عكس الجذر التربيعي الرئيسي لعشرة.»
تبسيط: ⓐ\(\sqrt{25}\) ⓑ\(\sqrt{121}\) ⓒ\(−\sqrt{144}\).
- إجابة
-
ⓐ
\(\begin{array}{ll} \text{} & \sqrt{25} \\ \text{Since }5^2=25 & 5 \end{array}\)ⓑ
\(\begin{array}{ll} \text{} & \sqrt{121} \\ \text{Since }11^2=121 & 11 \end{array}\)
ⓒ
\(\begin{array}{ll} {} & −\sqrt{144} \\ \text{The negative is in front of} & −12 \\ \text{the radical sign.} \end{array}\)
التبسيط: ⓐ\(\sqrt{36}\) ⓑ\(\sqrt{169}\) ⓒ\(−\sqrt{225}\)
- إجابة
-
ⓐ 6 ⓑ 13 ⓒ −15
التبسيط: ⓐ\(\sqrt{16}\) ⓑ\(\sqrt{196}\) ⓒ\(−\sqrt{100}\)
- إجابة
-
ⓐ 4 ⓑ 14 ⓒ −10
تحديد الأعداد الصحيحة والأعداد النسبية والأعداد غير النسبية والأعداد الحقيقية
لقد وصفنا بالفعل الأرقام على أنها عد الأرقام s والأرقام الصحيحة s والأعداد الصحيحة. ما الفرق بين هذه الأنواع من الأرقام؟ يمكن الخلط بين الاختلاف والطرح. ماذا عن السؤال عن كيفية التمييز بين هذه الأنواع من الأرقام؟
\[\begin{array}{ll} \text{Counting numbers} & 1,2,3,4,….. \\ \text{Whole numbers} & 0,1,2,3,4,…. \\ \text{Integers} & ….−3,−2,−1,0,1,2,3,…. \end{array}\]
ما نوع الأرقام التي سنحصل عليها إذا بدأنا بجميع الأعداد الصحيحة ثم أدرجنا جميع الكسور؟ تشكل الأرقام التي سنحصل عليها مجموعة الأرقام العقلانية. الرقم العقلاني هو رقم يمكن كتابته كنسبة من عددين صحيحين.
بشكل عام، أي رقم عشري ينتهي بعد عدد من الأرقام (مثل 7.3 أو −1.2684) هو رقم منطقي. يمكننا استخدام القيمة المكانية للرقم الأخير كمقام عند كتابة العدد العشري في صورة كسر. الرقم العشري\(\frac{1}{3}\) هو الرقم\(0.\overline{3}\). يشير الشريط الموجود فوق 3 إلى أن الرقم 3 يتكرر بلا حدود. باستمرار له معنى مهم في حساب التفاضل والتكامل. يُطلق على الرقم (الأرقام) الموجود أسفل الشريط اسم الكتلة المتكررة ويتكرر باستمرار.
نظرًا لأنه يمكن كتابة جميع الأعداد الصحيحة ككسر مقامه هو 1، فإن الأعداد الصحيحة (وكذلك العد والأرقام الصحيحة) هي أرقام عقلانية.
يمكن كتابة كل رقم منطقي كنسبة من الأعداد الصحيحة\(\frac{p}{q}\)، حيث p و q عبارة عن أعداد صحيحة\(q≠0\)، وكرقم عشري يتوقف أو يتكرر.
الرقم العقلاني هو رقم النموذج\(\frac{p}{q}\)، حيث p و q عبارة عن أعداد صحيحة و\(q≠0\).
يتوقف النموذج العشري الخاص به أو يتكرر.
هل هناك أي أرقام عشرية لا تتوقف أو تتكرر؟ نعم! الرقم (الحرف اليوناني pi، يُنطق «pie»)، وهو أمر مهم جدًا في وصف الدوائر، له شكل عشري لا يتوقف أو يتكرر. نستخدم ثلاث نقاط (...) للإشارة إلى أن الرقم العشري لا يتوقف أو يتكرر.
\[π=3.141592654...\]
الجذر التربيعي لرقم ليس مربعًا مثاليًا هو عدد عشري لا يتوقف أو يتكرر.
لا يمكن كتابة الأرقام التي لا يتوقف شكلها العشري أو يتكرر ككسر من الأعداد الصحيحة. نسمي هذا رقمًا غير منطقي.
الرقم غير العقلاني هو رقم لا يمكن كتابته كنسبة من عددين صحيحين.
لا يتوقف شكله العشري ولا يتكرر.
دعونا نلخص طريقة يمكننا استخدامها لتحديد ما إذا كان الرقم عقلانيًا أم غير منطقي.
إذا كان الشكل العشري للرقم
- يتكرر أو يتوقف، الرقم هو رقم عقلاني.
- لا يتكرر ولا يتوقف، الرقم هو رقم غير منطقي.
لقد رأينا أن جميع أرقام العد هي أعداد صحيحة، وجميع الأرقام الصحيحة هي أعداد صحيحة، وجميع الأعداد الصحيحة هي أرقام عقلانية. الأرقام غير المنطقية هي الأرقام التي لا يتوقف شكلها العشري ولا يتكرر. عندما نجمع الأعداد النسبية والأرقام غير المنطقية، نحصل على مجموعة الأعداد الحقيقية s.
الرقم الحقيقي هو رقم عقلاني أو غير منطقي.
سنقدم لاحقًا في هذه الدورة أرقامًا تتجاوز الأرقام الحقيقية. يوضح الشكل كيف تتلاءم مجموعات الأرقام التي استخدمناها حتى الآن معًا.
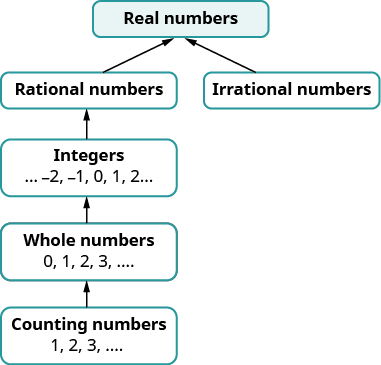
هل يبدو مصطلح «الأرقام الحقيقية» غريبًا بالنسبة لك؟ هل هناك أي أرقام غير «حقيقية»، وإذا كان الأمر كذلك، فماذا يمكن أن تكون؟ هل يمكننا التبسيط\(−\sqrt{25}\)؟ هل هناك رقم مربعه\(−25\)؟
\[()^2=−25?\]
لا يحتوي أي من الأرقام التي تعاملنا معها حتى الآن على مربع\(−25\). لماذا؟ أي رقم موجب مربع يكون موجبًا. أي رقم سالب مربّع يكون موجبًا. لذلك نقول أنه لا يوجد رقم حقيقي يساوي\(\sqrt{−25}\). الجذر التربيعي للرقم السالب ليس رقمًا حقيقيًا.
بالنظر إلى الأرقام\(−7,\frac{14}{5},8,\sqrt{5},5.9,−\sqrt{64}\)، قم بإدراج ⓐ الأرقام الصحيحة ⓑ الأعداد الصحيحة ⓒ الأرقام العقلانية ⓓ الأرقام غير المنطقية ⓔ الأرقام الحقيقية.
- إجابة
-
ⓐ تذكر أن الأرقام الصحيحة هي،\(0,1,2,3,…,\) لذا فإن 8 هو الرقم الصحيح الوحيد المعطى.
ⓑ الأعداد الصحيحة هي الأرقام الصحيحة وأضدادها (والتي تتضمن 0). لذا فإن العدد الكامل 8 هو عدد صحيح، و−7 هو عكس عدد صحيح، لذا فهو عدد صحيح أيضًا. لاحظ أيضًا أن 64 هو مربع 8 إذن\(−\sqrt{64}=−8\). لذا فإن الأعداد الصحيحة هي\(−7,8,\) و\(−\sqrt{64}\).
ⓒ بما أن جميع الأعداد الصحيحة عقلانية، إذن\(−7,8,\)\(−\sqrt{64}\) فهي عقلانية. تتضمن الأرقام العقلانية أيضًا الكسور والأرقام العشرية التي تتكرر أو تتوقف،\(\frac{14}{5}\) وهكذا\(5.9\) تكون منطقية. لذا فإن قائمة الأرقام العقلانية هي\(−7,\frac{14}{5},8,5.9,\) و\(−\sqrt{64}\).
ⓓ تذكر أن الرقم 5 ليس مربعًا مثاليًا، لذا فهو\(\sqrt{5}\) أمر غير منطقي.
ⓔ جميع الأرقام المدرجة هي أرقام حقيقية.
بالنظر إلى\(−3,−\sqrt{2},0.\overline{3},\frac{9}{5},4,\sqrt{49},\) قائمة الأرقام، فإن ⓐ الأرقام الصحيحة ⓑ الأعداد الصحيحة ⓒ الأرقام العقلانية
ⓓ أرقام غير منطقية ⓔ أرقام حقيقية.
- إجابة
-
ⓐ\(4,\sqrt{49}\) ⓑ\(−3,4,\sqrt{49}\)
ⓒ\(−3,0.\overline{3},\frac{9}{5},4,\sqrt{49}\) ⓓ\(−\sqrt{2}\)ⓔ\(−3,−\sqrt{2},0.\overline{3},\frac{9}{5},4,\sqrt{49}\)
\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121},2.041975...,\)تسرد الأرقام المعطاة ⓐ الأرقام الصحيحة ⓑ الأعداد الصحيحة ⓒ الأرقام العقلانية ⓓ الأرقام غير المنطقية ⓔ الأرقام الحقيقية.
- إجابة
-
ⓐ\(6,\sqrt{121}\)
ⓑ\(−\sqrt{25},−1,6,\sqrt{121}\)
ⓒ\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121}\)
ⓓ\(2.041975...\)
ⓔ\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121},2.041975...\)
حدد موقع الكسور والأعداد العشرية على خط الأعداد
نريد الآن تضمين الكسور والأعداد العشرية على خط الأعداد. لنبدأ بالكسور وتحديد الموقع\(\frac{1}{5},−\frac{4}{5},3,\frac{7}{4},−\frac{9}{2},−5\)\(\frac{8}{3}\) وعلى خط الأعداد.
سنبدأ بالأعداد الصحيحة 3 و−5 لأنها أسهل طريقة للرسم. انظر الشكل.
الكسور المناسبة المدرجة هي\(\frac{1}{5}\)\(−\frac{4}{5}.\) ونعلم أن الكسر المناسب\(\frac{1}{5}\) له قيمة أقل من واحد وبالتالي سيكون بين 0 و 1. المقام هو 5، لذلك نقسم الوحدة من 0 إلى 1 إلى 5 أجزاء متساوية\(\frac{1}{5},\frac{2}{5},\frac{3}{5},\frac{4}{5}\). نحن نتآمر\(\frac{1}{5}\).
وبالمثل،\(−\frac{4}{5}\) يتراوح بين 0 و−1. بعد تقسيم الوحدة إلى 5 أجزاء متساوية نرسم\(−\frac{4}{5}\).
أخيرًا، انظر إلى الكسور غير الصحيحة\(\frac{7}{4},\frac{9}{2},\frac{8}{3}\). قد يكون تحديد موقع هذه النقاط أسهل إذا قمت بتغيير كل منها إلى رقم مختلط.
\[\dfrac{7}{4}=1\dfrac{3}{4} \; \; \; \; \; \; \; \; \; −\dfrac{9}{2}=−4\dfrac{1}{2} \; \; \; \; \; \; \; \; \; \dfrac{8}{3}=2\dfrac{2}{3}\]
يوضح الشكل خط الأرقام مع رسم جميع النقاط.

حدد موقع ما يلي وقم بتسميته على سطر الأرقام:\(4,\frac{3}{4},−\frac{1}{4},−3,\frac{6}{5},−\frac{5}{2},\) و\(\frac{7}{3}\).
- إجابة
-
حدد موقع الأعداد الصحيحة ورسمها،\(4,−3.\)
حدد موقع الكسر المناسب\(\frac{3}{4}\) أولاً. \(\frac{3}{4}\)يقع الكسر بين 0 و1. قسّم المسافة بين 0 و 1 إلى أربعة أجزاء متساوية، ثم نرسم\(\frac{3}{4}\). مؤامرة مماثلة\(−\frac{1}{4}\).
الآن حدد موقع الكسور غير الصحيحة\(\frac{6}{5},−\frac{5}{2},\) و\(\frac{7}{3}\). من الأسهل رسمها إذا قمنا بتحويلها إلى أرقام مختلطة ثم رسمها كما هو موضح أعلاه:\(\frac{6}{5}=1\frac{1}{5},−\frac{5}{2}=−2\frac{1}{2},\frac{7}{3}=2\frac{1}{3}\).

حدد موقع ما يلي وقم بتسميته على سطر الأرقام:\(−1,\frac{1}{3},\frac{6}{5},−\frac{7}{4},\frac{9}{2},5,−\frac{8}{3}\).
- إجابة
-
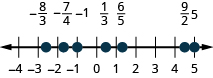
حدد موقع ما يلي وقم بتسميته على سطر الأرقام:\(−2,\frac{2}{3},\frac{7}{5},−\frac{7}{4},\frac{7}{2},3,−\frac{7}{3}\).
- إجابة
-
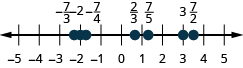
نظرًا لأن الأعداد العشرية هي أشكال من الكسور، فإن تحديد موضع الأعداد العشرية على خط الأعداد يشبه تحديد موقع الكسور على خط الأعداد.
حدد الموقع على خط الأعداد: ⓐ 0.4 ⓑ −0.74.
- إجابة
-
ⓐ الرقم العشري 0.4 يعادل الكسر المناسب\(\frac{4}{10}\)، لذلك يقع 0.4 بين 0 و 1. في خط الأعداد، قسّم الفاصل الزمني بين 0 و1 إلى 10 أجزاء متساوية. الآن قم بتسمية الأجزاء 0.1، 0.2، 0.3، 0.4، 0.5، 0.6، 0.7، 0.8، 0.9، 1.0. نكتب 0 كـ 0.0 و1 كـ 1.0، بحيث تكون الأرقام ثابتة في الأجزاء من عشرة. أخيرًا، ضع علامة 0.4 على خط الأعداد.

ⓑ الرقم العشري\(−0.74\) يعادل\(−\frac{74}{100}\)، لذا فهو يقع بين 0 و.−1. على خط الأعداد، ضع علامة على الأجزاء من مائة في الفترة بين 0 و−1.

حدد موقع على خط الأرقام: ⓐ\(0.6\) ⓑ\(−0.25.\)
- إجابة
-
ⓐ

ⓑ
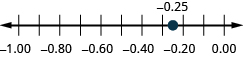
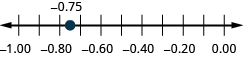
حدد الموقع على خط الأعداد: ⓐ 0.90.9 ⓑ −0.75.−0.75.
- إجابة
-
ⓐ

ⓑ
قم بالوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات إضافية وممارسة باستخدام الأرقام العشرية.
- أساسيات الحساب: قسمة الأعداد العشرية
المفاهيم الرئيسية
- كيفية تقريب الأعداد العشرية.
- حدد القيمة المكانية المحددة وقم بتمييزها بسهم.
- ضع خط تحت الرقم الموجود على يمين القيمة المكانية.
- هل الرقم المسطر أكبر من أو يساوي 5؟
- نعم: أضف 1 إلى الرقم في القيمة المكانية المحددة.
- لا: لا تقم بتغيير الرقم في القيمة المكانية المحددة
- أعد كتابة الرقم، مع حذف جميع الأرقام الموجودة على يمين رقم التقريب.
- كيفية إضافة أو طرح الكسور العشرية.
- حدد علامة المجموع أو الفرق.
- اكتب الأرقام بحيث تصطف النقاط العشرية رأسيًا.
- استخدم الأصفار كعناصر نائبة، حسب الحاجة.
- قم بإضافة الأرقام أو طرحها كما لو كانت أرقامًا صحيحة. ثم ضع النقطة العشرية في الإجابة تحت النقاط العشرية في الأرقام المعطاة.
- اكتب المجموع أو الفرق مع العلامة المناسبة
- كيفية ضرب الأرقام العشرية.
- حدد علامة المنتج.
- اكتب في شكل عمودي، واصطف الأرقام على اليمين. اضرب الأرقام كما لو كانت أرقامًا كاملة، مع تجاهل النقاط العشرية مؤقتًا.
- ضع النقطة العشرية. عدد المنازل العشرية في المنتج هو مجموع عدد المنازل العشرية في العوامل.
- اكتب المنتج بالعلامة المناسبة.
- كيفية ضرب عدد عشري في قوة عشرة.
- انقل النقطة العشرية إلى اليمين بنفس عدد الأماكن مثل عدد الأصفار بقوة 10.
- أضف الأصفار في نهاية الرقم حسب الحاجة.
- كيفية تقسيم الأرقام العشرية.
- حدد علامة حاصل القسمة.
- اجعل المقسوم رقمًا صحيحًا عن طريق «نقل» العلامة العشرية إلى اليمين. «انقل» النقطة العشرية في التوزيعات بنفس عدد المواضع - بإضافة الأصفار حسب الحاجة.
- يقسم. ضع النقطة العشرية في حاصل القسمة فوق النقطة العشرية في التوزيعات.
- اكتب حاصل القسمة مع العلامة المناسبة.
- كيفية تحويل عدد عشري إلى كسر مناسب وكسر إلى رقم عشري.
- لتحويل عدد عشري إلى كسر صحيح، حدد القيمة المكانية للرقم النهائي.
- اكتب الكسر.
- البسط - «الأرقام» الموجودة على يمين العلامة العشرية
- القاسم - القيمة المكانية المقابلة للرقم النهائي
- لتحويل كسر إلى رقم عشري، قسّم بسط الكسر على مقام الكسر.
- كيفية تحويل نسبة مئوية إلى عدد عشري وعشرية إلى نسبة مئوية.
- لتحويل نسبة مئوية إلى عدد عشري، انقل العلامة العشرية إلى اليسار بعد إزالة علامة النسبة المئوية.
- لتحويل عدد عشري إلى نسبة مئوية، انقل العلامة العشرية منزلتين إلى اليمين ثم أضف علامة النسبة المئوية.
- \(\sqrt{m}\)تتم قراءة تدوين الجذر التربيعي «الجذر التربيعي لـ m». إذا\(m=n^2\)، إذن\(\sqrt{m}=n\)، من أجل\(n≥0\). الجذر التربيعي لـ m،\(\sqrt{m}\)، هو الرقم الموجب الذي مربعه هو m.
- منطقي أو غير منطقي إذا كان الشكل العشري لعدد
- يتكرر أو يتوقف، الرقم هو رقم عقلاني.
- لا يتكرر ولا يتوقف، الرقم هو رقم غير منطقي.
- أرقام حقيقية
.jpg)
الشكل 4.
مسرد المصطلحات
- رقم غير منطقي
- الرقم غير العقلاني هو رقم لا يمكن كتابته كنسبة من عددين صحيحين. لا يتوقف شكله العشري ولا يتكرر.
- بالمائة
- النسبة المئوية هي نسبة مقامها 100.
- الجذر التربيعي الرئيسي
- يسمى الجذر التربيعي الموجب بالجذر التربيعي الرئيسي.
- رقم عقلاني
- الرقم العقلاني هو رقم النموذج\(\frac{p}{q}\)، حيث p و q عبارة عن أعداد صحيحة و\(q≠0\). يتوقف النموذج العشري الخاص به أو يتكرر.
- رقم حقيقي
- الرقم الحقيقي هو رقم عقلاني أو غير منطقي.
- مربع الرقم
- إذا كان\(n^2=m\) m هو مربع n.
- الجذر التربيعي لعدد
- إذا كان\(n^2=m\) n هو الجذر التربيعي لـ m.


