1.4: الكسور

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

• تبسيط الكسور
• ضرب الكسور وقسمتها
• جمع الكسور وطرحها
• استخدم ترتيب العمليات لتبسيط الكسور
• إيجاد قيمة التعبيرات المتغيرة بالكسور

يمكن العثور على مقدمة أكثر شمولاً للموضوعات التي يتم تناولها في هذا القسم في فصل الجبر الأولي، الأسس.

تبسيط الكسور

الكسر هو طريقة لتمثيل أجزاء من الكل. \(\frac{2}{3}\)يمثل الكسر اثنين من ثلاثة أجزاء متساوية (الشكل\(\PageIndex{1}\)). في الكسر\(\frac{2}{3}\)، يُطلق على 2 اسم البسط بينما يُطلق على 3 اسم المقام. يُطلق على الخط اسم شريط الكسر.

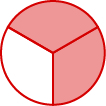
الشكل\(\PageIndex{1}\): في الدائرة،\(\frac{2}{3}\) يتم تظليل الدائرة —2 من الأجزاء الثلاثة المتساوية.

كسر

يتم كتابة الكسر وأين\(\dfrac{a}{b}\)\(b\neq 0\) و

\(a\)هو البسط\(b\) والمقام.

يمثل الكسر أجزاء من الكل. المقام\(b\) هو عدد الأجزاء المتساوية التي تم تقسيم الكل إليها،\(a\) ويشير البسط إلى عدد الأجزاء المضمنة.

الكسور التي لها نفس القيمة هي كسور مكافئة. الكسور المتكافئة

تسمح لنا الخاصية بالعثور على الكسور المتكافئة وكذلك تبسيط الكسور.

إذا كانت الأرقام\(a\)\(b\)، وما\(c\) زالت\(b\neq 0,c\neq 0\)، أين،

ثم\(\dfrac{a}{b}=\dfrac{a·c}{b·c}\) و\(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\)

يعتبر الكسر مبسطًا إذا لم تكن هناك عوامل مشتركة، بخلاف 1، في البسط والمقام.

على سبيل المثال،

\(\dfrac{2}{3}\)تم تبسيطه نظرًا لعدم وجود عوامل مشتركة لـ\(2\) و\(3\).

\(\dfrac{10}{15}\)لم يتم تبسيطه لأنه\(5\) عامل مشترك لـ\(10\) و\(15\).

نقوم بتبسيط الكسر أو تقليله عن طريق إزالة العوامل المشتركة للبسط والمقام. لا يتم تبسيط الكسر حتى تتم إزالة جميع العوامل الشائعة. إذا كان التعبير يحتوي على كسور، فلن يتم تبسيطه تمامًا حتى يتم تبسيط الكسور.

في بعض الأحيان قد لا يكون من السهل العثور على العوامل المشتركة للبسط والمقام. عندما يحدث هذا، فإن الفكرة الجيدة هي حساب البسط والمقام في أعداد أولية. ثم قسّم العوامل المشتركة باستخدام خاصية الكسور المتكافئة.

قم بالتبسيط\(\dfrac{−315}{770}\).

إجابة

قم بالتبسيط\(−\dfrac{69}{120}\).

إجابة

\(−\dfrac{23}{40}\)

مثال\(\PageIndex{3}\)

قم بالتبسيط\(−\dfrac{120}{192}\).

إجابة

\(−\dfrac{5}{8}\)

نلخص الآن الخطوات التي يجب اتباعها لتبسيط الكسور.

قم بتبسيط الكسر.

1. أعد كتابة البسط والمقام لإظهار العوامل المشتركة.
   إذا لزم الأمر، قم بحساب البسط والمقام في أعداد أولية أولاً.
2. قم بتبسيط استخدام خاصية الكسور المتكافئة من خلال تقسيم العوامل المشتركة.
3. اضرب أي عوامل متبقية.

ضرب الكسور وقسمتها

يجد العديد من الأشخاص أن ضرب الكسور وقسمتها أسهل من جمع الكسور وطرحها.

لضرب الكسور، نضرب البسط ونضرب المقامات.

ضرب الكسور

إذا كانت\(d\) الأرقام\(a\)\(b\)\(c\)،، و\(b≠0\)، وأين\(d≠0\)، ثم

\[\frac{a}{b}·\frac{c}{d}=\frac{ac}{bd}\]

لضرب الكسور، اضرب البسط واضرب المقامات.

عند ضرب الكسور، لا تزال خصائص الأرقام الموجبة والسالبة سارية بالطبع. من الجيد تحديد علامة المنتج كخطوة أولى. على سبيل المثال، سنضرب السالب والإيجابي، لذلك سيكون المنتج سلبيًا.

عند ضرب كسر في عدد صحيح، قد يكون من المفيد كتابة العدد الصحيح ككسر. يمكن كتابة أي عدد صحيح، a، كـ\(\dfrac{a}{1}\). لذلك، على سبيل المثال،\(3=\dfrac{3}{1}\).

التمارين\(\PageIndex{4}\)

اضرب:\(−\dfrac{12}{5}(−20x).\)

إجابة

الخطوة الأولى هي العثور على علامة المنتج. نظرًا لأن العلامات هي نفسها، فإن المنتج إيجابي.

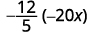
حدد علامة المنتج. العلامات هي نفسها، لذا فإن المنتج إيجابي.
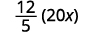
اكتب ٢٠ × في صورة كسر.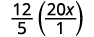
اضرب.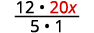
أعد كتابة 20 لإظهار العامل المشترك 5 وقسمه.
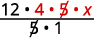
قم بالتبسيط.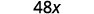

التمارين\(\PageIndex{5}\)

اضرب:\(\dfrac{1}{13}(−9a)\).

إجابة

\(−33a\)

التمارين\(\PageIndex{6}\)

اضرب:\(\dfrac{13}{7}(−14b)\).

إجابة

\(−26b\)

الآن بعد أن عرفنا كيفية ضرب الكسور، أصبحنا مستعدين تقريبًا للقسمة. قبل أن نتمكن من القيام بذلك، نحتاج إلى بعض المفردات. يُوجد مقلوب الكسر بقلب الكسر، ووضع البسط في المقام والمقام في البسط. المعاملة بالمثل\(\frac{2}{3}\) هي\(\frac{3}{2}\). نظرًا لأن الرقم 4 مكتوب في صورة كسرية\(\frac{4}{1}\)، فإن مقلوب 4 هو\(\frac{1}{4}\).

لتقسيم الكسور، نضرب الكسر الأول في مقلوب الثاني.

قسم الكسر

إذا كانت الأرقام\(a\)\(b\)\(c\)،،، وما\(d\) هي\(b≠0\)\(c≠0\)، وأين\(d≠0\)، ثم

\[\frac{a}{b}÷\frac{c}{d}=\frac{a}{b}⋅\frac{d}{c}\]

لتقسيم الكسور، نضرب الكسر الأول في مقلوب الثاني.

علينا أن نقول\(b≠0\)\(c≠0\)\(d≠0\)، وللتأكد من أننا لا نقسم على الصفر!

التمارين\(\PageIndex{7}\)

ابحث عن حاصل القسمة:\(−\dfrac{7}{18}÷(−\dfrac{14}{27}).\)

إجابة

	\(−\dfrac{7}{18}÷(−\dfrac{14}{27})\)
للقسمة، اضرب الكسر الأول في مقلوب الثاني.
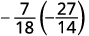
حدد علامة المنتج، ثم اضرب.
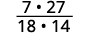
أعد كتابة عرض العوامل المشتركة.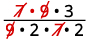
قم بإزالة العوامل المشتركة.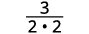
قم بالتبسيط.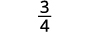

قسّم:\(−\dfrac{7}{27}÷(−\dfrac{35}{36})\).

إجابة

\(\dfrac{4}{15}\)

التمارين\(\PageIndex{9}\)

قسّم:\(−\dfrac{5}{14}÷(−\dfrac{15}{28}).\)

إجابة

\(\dfrac{2}{3}\)

تحتوي البسط أو القواسم لبعض الكسور على الكسور نفسها. يسمى الكسر الذي يكون فيه البسط أو المقام كسرًا بالكسر المركب.

تعريف: كسر معقد

الكسر المركب هو كسر يحتوي فيه البسط أو المقام على كسر.

بعض الأمثلة على الكسور المعقدة هي:

\[\dfrac{\frac{6}{7}}{3} \quad \dfrac{\frac{3}{4}}{\frac{5}{8}} \quad \dfrac{\frac{x}{2}}{ \frac{5}{6}}\]

لتبسيط الكسر المعقد، تذكر أن شريط الكسر يعني القسمة. على سبيل المثال،\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) يعني الكسر المعقد\(\dfrac{3}{4}÷\frac{5}{8}.\)

التمارين\(\PageIndex{10}\)

قم بالتبسيط:\(\dfrac{\dfrac{x}{2}}{ \dfrac{xy}{6}}\).

إجابة

\(\begin{array}{lc} \text{} & \dfrac{\dfrac{x}{2}}{ \dfrac{xy}{6}} \\[6pt] \text{Rewrite as division.} & \dfrac{x}{2}÷\dfrac{xy}{6} \\[6pt] \text{Multiply the first fraction by the reciprocal of the second.} & \dfrac{x}{2}·\dfrac{6}{xy} \\[6pt] \text{Multiply.} & \dfrac{x·6}{2·xy} \\[6pt] \text{Look for common factors.} & \dfrac{ \cancel{x}·3·\cancel{2}}{\cancel{2}·\cancel{x}·y} \\[6pt] \text{Divide common factors and simplify.} & \dfrac{3}{y} \end{array}\)

قم بالتبسيط:\(\dfrac{\dfrac{a}{8}}{ \dfrac{ab}{6}}\).

إجابة

\(\dfrac{3}{4b}\)

قم بالتبسيط:\(\dfrac{\dfrac{p}{2}}{ \dfrac{pq}{8}}\).

إجابة

\(\dfrac{4}{q}\)

جمع الكسور وطرحها

عندما نضرب الكسور، نضرب البسط ونضرب المقامات مباشرة. لجمع الكسور أو طرحها، يجب أن يكون لها قاسم مشترك.

جمع الكسور والطرح

إذا كانت الأرقام\(a\)\(b\)، وما\(c\) هي، فأين\(c≠0\)، إذن

\[\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \text{ and } \dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\]

لجمع الكسور أو طرحها، قم بجمع البسط أو طرحه ووضع النتيجة فوق المقام المشترك.

القاسم المشترك الأصغر (LCD) لكسرين هو أصغر رقم يمكن استخدامه كقاسم مشترك للكسور. شاشة LCD الخاصة بالكسرين هي المضاعف المشترك الأصغر (LCM) لمقاساتهما.

القاسم المشترك الأصغر

القاسم المشترك الأصغر (LCD) لكسرين هو المضاعف المشترك الأصغر (LCM) لمقاساتهما.

بعد العثور على المقام المشترك الأصغر لكسرين، نقوم بتحويل الكسور إلى كسور مكافئة باستخدام شاشة LCD. يتيح لنا تجميع هذه الخطوات جمع الكسور وطرحها لأن مقاماتها ستكون هي نفسها!

مثال\(\PageIndex{13}\): How to Add or Subtract Fractions

إضافة:\(\dfrac{7}{12}+\dfrac{5}{18}\).

إجابة

مثال\(\PageIndex{14}\)

إضافة:\(\dfrac{7}{12}+\dfrac{11}{15}\).

إجابة

\(\dfrac{79}{60}\)

مثال\(\PageIndex{15}\)

إضافة:\(\dfrac{13}{15}+\dfrac{17}{20}\).

إجابة

\(\dfrac{103}{60}\)

قم بجمع الكسور أو طرحها.

1. هل لديهم قاسم مشترك؟
   • نعم - انتقل إلى الخطوة 2.
   • لا - أعد كتابة كل جزء باستخدام شاشة LCD (القاسم المشترك الأقل).
     • ابحث عن شاشة LCD.
     • قم بتغيير كل جزء إلى كسر مكافئ باستخدام شاشة LCD كمقامه.
2. قم بإضافة الكسور أو طرحها.
3. قم بالتبسيط، إن أمكن.

لدينا الآن جميع العمليات الأربع للكسور. يلخص الجدول عمليات الكسر.

ضرب الكسور	قسم الكسر
\(\dfrac{a}{b}⋅\dfrac{c}{d}=\dfrac{ac}{bd}\)	\(\dfrac{a}{b}÷\dfrac{c}{d}=\dfrac{a}{b}⋅\dfrac{d}{c}\)
اضرب البسط واضرب القواسم	اضرب الكسر الأول في مقلوب الثاني.
إضافة الكسر	طرح الكسر
\(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c}\)	\(\dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\)
اجمع البسط ثم ضع المجموع فوق المقام المشترك.	اطرح البسط ثم ضع الفرق على المقام المشترك.
لمضاعفة الكسور أو تقسيمها، لا توجد حاجة إلى شاشة LCD. لإضافة أو طرح الكسور، يلزم وجود شاشة LCD.

عند بدء التمرين، حدد العملية دائمًا ثم تذكر الطرق اللازمة لهذه العملية.

تبسيط: ⓐ\(\dfrac{5x}{6}−\dfrac{3}{10}\) ⓑ\(\dfrac{5x}{6}·\dfrac{3}{10}\).

إجابة

اسأل أولاً، «ما هي العملية؟» تحديد العملية سيحدد ما إذا كنا بحاجة إلى قاسم مشترك أم لا. تذكر أننا نحتاج إلى قاسم مشترك للجمع أو الطرح، ولكن ليس للضرب أو القسمة.

ⓐ

\ (\ ابدأ {المصفوفة} {lc}\ text {ما هي العملية؟ العملية هي الطرح.}\\ [6pt]\ text {هل للكسور قاسم مشترك؟ رقم.} &\ dfrac {5x} {6} −\ dfrac {3} {10}\\ [6pt]\ النص {ابحث عن شاشة LCD لـ} 6\ النص {و} 10\\ النص {شاشة ال سي دي هي 30.}\\\ [6pt] {\\ ابدأ {محاذاة} 6 و =2· 3\\\ [6pt]
\;\;\\ [6pt]\;\;\;\;\;\;\;\;\\ تسطير {=2· 5\;\;\;\;}\\ [6pt]
\\ النص {LCD} & =2·3· 5\\ [6 pt]
\ text {LCD} & =30\ end {align*}}\\ [6pt]\\\
\ text {أعد كتابة كل كسر في صورة كسر مكافئ مع شاشة LCD.} &\ dfrac {5x·5} {6· 5} −\ dfrac {3·3} {10·3}\\\ [6pt]
\ text {} &\ dfrac {25x} {30} −\ dfrac {9} {30}\\ [6pt]\ [6pt]
\ النص {طرح البسط ووضع}\\ [6pt]\ [6pt]
\ النص {الفرق على النص الشائع القواسم.} &\ dfrac {25x−9} {30}\\ [6pt]\\\
\ النص {التبسيط، إن أمكن. لا توجد عوامل مشتركة.}\\ [6pt]
\ text {تم تبسيط الكسر.} \ end {مصفوفة}\)

ⓑ

\(\begin{array}{lc} \text{What is the operation? Multiplication.} & \dfrac{25x}{6}·\dfrac{3}{10} \\ \text{To multiply fractions,multiply the numerators} \\ \text{and multiply the denominators.} & \dfrac{25x·3}{6·10} \\ \text{Rewrite, showing common factors.} \\ \text{Remove common factors.} & \dfrac{\cancel{5} x · \cancel{3}}{2·\cancel{3}·2·\cancel{5}} \\ \text{Simplify.} & \dfrac{x}{4} \end{array}\)

لاحظ أننا كنا بحاجة إلى شاشة LCD للإضافة\(\dfrac{25x}{6}−\dfrac{3}{10}\)، ولكن ليس للتكاثر\(\dfrac{25x}{6}⋅\dfrac{3}{10}\).

مثال\(\PageIndex{17}\)

تبسيط: ⓐ\(\dfrac{3a}{4}−\dfrac{8}{9}\) ⓑ\(\dfrac{3a}{4}·\dfrac{8}{9}\).

إجابة

ⓐ\(\dfrac{27a−32}{36}\) ⓑ\(\dfrac{2a}{3}\)

مثال\(\PageIndex{18}\)

تبسيط: ⓐ\(\dfrac{4k}{5}−\dfrac{1}{6}\) ⓑ\(\dfrac{4k}{5}⋅\dfrac{1}{6}\).

إجابة

ⓐ\(\dfrac{24k−5}{30}\) ⓑ\(\dfrac{2k}{15}\)

استخدم ترتيب العمليات لتبسيط الكسور

يعمل شريط الكسر في الكسر كرمز تجميع. ثم يخبرنا ترتيب العمليات بتبسيط البسط ثم المقام. ثم نقسم.

قم بتبسيط التعبير باستخدام شريط الكسر.

1. قم بتبسيط التعبير في البسط. قم بتبسيط التعبير في المقام.
2. قم بتبسيط الكسر.

أين تذهب العلامة السالبة في الكسر؟ عادةً ما تكون العلامة السالبة أمام الكسر، لكنك سترى أحيانًا كسرًا ببسط سالب، أو أحيانًا بمقام سالب. تذكر أن الكسور تمثل القسمة. عندما تكون علامات البسط والمقام مختلفة، يكون حاصل القسمة سالبًا.

\[\dfrac{−1}{3}=−\dfrac{1}{3} \; \; \; \; \; \; \dfrac{\text{negative}}{\text{positive}}=\text{negative}\]

\[\dfrac{1}{−3}=−\dfrac{1}{3} \; \; \; \; \; \; \dfrac{\text{positive}}{\text{negative}}=\text{negative}\]

وضع علامة سالبة في الكسر

للحصول على أي أرقام إيجابية\(a\) و\(b\)،

\[\dfrac{−a}{b}=\dfrac{a}{−b}=−\dfrac{a}{b}\]

مثال\(\PageIndex{19}\)

قم بالتبسيط:\(\dfrac{4(−3)+6(−2)}{−3(2)−2}\).

إجابة

يعمل شريط الكسر كرمز تجميع. لذا قم بتبسيط البسط والمقام بشكل منفصل.

\(\begin{array}{lc} \text{} & \dfrac{4(−3)+6(−2)}{−3(2)−2} \\[5pt] \text{Multiply.} & \dfrac{−12+(−12)}{−6−2} \\[5pt] \text{Simplify.} & \dfrac{−24}{−8} \\[5pt] \text{Divide.} & 3 \end{array}\)

مثال\(\PageIndex{20}\)

قم بالتبسيط:\(\dfrac{8(−2)+4(−3)}{−5(2)+3}\).

إجابة

4

مثال\(\PageIndex{21}\)

قم بالتبسيط:\(\dfrac{7(−1)+9(−3)}{−5(3)−2}\).

إجابة

2

سننظر الآن في الكسور المعقدة حيث يحتوي البسط أو المقام على تعبير يمكن تبسيطه. لذلك يجب علينا أولاً تبسيط البسط والمقام بشكل منفصل باستخدام ترتيب العمليات. ثم نقسم البسط على المقام لأن شريط الكسر يعني القسمة.

مثال\(\PageIndex{22}\): How to Simplify Complex Fractions

قم بالتبسيط:\(\dfrac{\left(\frac{1}{2}\right)^2}{4+3^2}\).

إجابة

مثال\(\PageIndex{23}\)

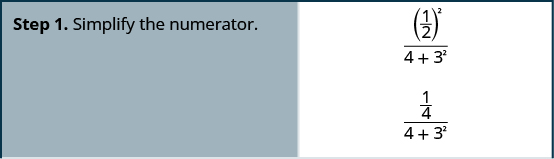
قم بالتبسيط:\(\dfrac{\left(\frac{1}{3}\right)^2}{2^3+2}\).

إجابة

\(\frac{1}{90}\)

مثال\(\PageIndex{24}\)

قم بالتبسيط:\(\dfrac{1+4^2}{\left(\frac{1}{4}\right)^2}\).

إجابة

272

قم بتبسيط الكسور المعقدة.

1. قم بتبسيط البسط.
2. قم بتبسيط المقام.
3. اقسم البسط على المقام. قم بالتبسيط إن أمكن.

مثال\(\PageIndex{25}\)

قم بالتبسيط:\(\dfrac{\dfrac{1}{2}+\dfrac{2}{3}}{\dfrac{3}{4}−\dfrac{1}{6}}\).

إجابة

قد يساعد وضع الأقواس حول البسط والمقام.

\(\begin{array}{lc}\text{} & \dfrac{\dfrac{1}{2}+\dfrac{2}{3}}{\dfrac{3}{4}−\dfrac{1}{6}} \\[6pt] \text{Simplify the numerator }(LCD=6)\text{ and } \\[6pt] \text{simplify the denominator }(LCD=12). & \dfrac{\left(\dfrac{3}{6}+\dfrac{4}{6}\right)}{\left(\dfrac{9}{12}−\dfrac{2}{12}\right)} \\[6pt] \text{Simplify.} & \left(\dfrac{7}{6}\right)\left(\dfrac{7}{12}\right) \\[6pt] \text{Divide the numerator by the denominator.} & \dfrac{7}{6}÷\dfrac{7}{12} \\[6pt] \text{Simplify.} & \dfrac{7}{6}⋅\dfrac{12}{7} \\[6pt] \text{Divide out common factors.} & \dfrac{\cancel{7}⋅\cancel{6}⋅2}{ \cancel{6}⋅\cancel{7}⋅1} \\[6pt] \text{Simplify.} & 2 \end{array}\)

مثال\(\PageIndex{26}\)

قم بالتبسيط:\( \dfrac{\dfrac{1}{3}+\dfrac{1}{2}}{ \dfrac{3}{4}−\dfrac{1}{3}}\).

إجابة

2

مثال\(\PageIndex{27}\)

قم بالتبسيط:\(\dfrac{\dfrac{2}{3}−\dfrac{1}{2}}{ \dfrac{1}{4}+\dfrac{1}{3}}\).

إجابة

\(\frac{2}{7}\)

إيجاد قيمة التعبيرات المتغيرة التي تحتوي على كسور

لقد قمنا بتقييم التعبيرات من قبل، ولكن يمكننا الآن تقييم التعبيرات بالكسور. تذكر أنه لتقييم التعبير، نستبدل قيمة المتغير في التعبير ثم نبسطه.

مثال\(\PageIndex{28}\)

قم بتقييم\(2x^2y\) متى\(x=\frac{1}{4}\) و\(y=−\frac{2}{3}\).

إجابة

استبدل القيم في التعبير.

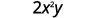
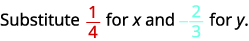
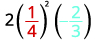
قم بتبسيط الأسس أولاً.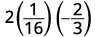
اضرب؛ قسّم العوامل المشتركة. لاحظ أننا نكتب 16 كـ 2242 · 2 · 4 لتسهيل إزالة العوامل المشتركة.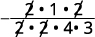
قم بالتبسيط.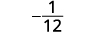

مثال\(\PageIndex{29}\)

قم بتقييم\(3ab^2\) متى\(a=−\frac{2}{3}\) و\(b=−\frac{1}{2}\).

إجابة

\(−\dfrac{1}{2}\)

مثال\(\PageIndex{30}\)

قم بتقييم\(4c^3d\) متى\(c=−\frac{1}{2}\) و\(d=−\frac{4}{3}\).

إجابة

\(\dfrac{2}{3}\)

يمكنك الوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات إضافية وممارسة باستخدام الكسور.

• جمع الكسور ذات المقامات المختلفة

المفاهيم الرئيسية

• إذا كانت الأرقام\(a\)\(b\)، وما\(c\) هي، فأين\(b≠0,c≠0\)، إذن

\(\dfrac{a}{b}=\dfrac{a·c}{b·c}\)و\(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\)

• كيفية تبسيط الكسر.
  1. أعد كتابة البسط والمقام لإظهار العوامل المشتركة.
     إذا لزم الأمر، قم بحساب البسط والمقام في أعداد أولية أولاً.
  2. قم بتبسيط استخدام خاصية الكسور المتكافئة من خلال تقسيم العوامل المشتركة.
  3. اضرب أي عوامل متبقية.
• إذا كانت\(d\) الأرقام\(a\)\(b\)\(c\)،، و\(b≠0\)، وأين\(d≠0\)، ثم

  \(\dfrac{a}{b}·\dfrac{c}{d}=\dfrac{ac}{bd}\)

  لضرب الكسور، اضرب البسط واضرب المقامات.

• إذا كانت الأرقام\(a\)\(b\)\(c\)،،، وما\(d\) هي\(b≠0\)\(c≠0\)، وأين\(d≠0\)، ثم

  \(\dfrac{a}{b}÷\dfrac{c}{d}=\dfrac{a}{b}⋅\dfrac{d}{c}\)

  لتقسيم الكسور، نضرب الكسر الأول في مقلوب الثاني.

• إذا كانت الأرقام\(a\)\(b\)، وما\(c\) هي، فأين\(c≠0\)، إذن

  \(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \text{ and } \dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\)

  لجمع الكسور أو طرحها، قم بجمع البسط أو طرحه ووضع النتيجة فوق المقام المشترك.

• كيفية جمع الكسور أو طرحها.
  1. هل لديهم قاسم مشترك؟
     • نعم - انتقل إلى الخطوة 2.
     • لا - أعد كتابة كل جزء باستخدام شاشة LCD (القاسم المشترك الأقل).
       • ابحث عن شاشة LCD.
       • قم بتغيير كل جزء إلى كسر مكافئ باستخدام شاشة LCD كمقامه.
  2. قم بإضافة الكسور أو طرحها.
  3. قم بالتبسيط، إن أمكن.
• كيفية تبسيط التعبير باستخدام شريط الكسر.
  1. قم بتبسيط التعبير في البسط. قم بتبسيط التعبير في المقام.
  2. قم بتبسيط الكسر.
• لأي أرقام إيجابية\(a\) و\(b\)،

  \(\dfrac{−a}{b}=\dfrac{a}{−b}=−\dfrac{a}{b}\)

• كيفية تبسيط الكسور المعقدة.
  1. قم بتبسيط البسط.
  2. قم بتبسيط المقام.
  3. اقسم البسط على المقام. قم بالتبسيط إن أمكن.

مسرد المصطلحات

كسر معقد

يسمى الكسر الذي يكون فيه البسط أو المقام كسرًا بالكسر المركب.

المقام - صفة مشتركة - حالة

في كسر مكتوب\(\dfrac{a}{b}\)\(b≠0\)، حيث يكون المقام\(b\) هو عدد الأجزاء المتساوية التي تم تقسيم الكل إليها.

الكسور المكافئة

الكسور المتكافئة هي الكسور التي لها نفس القيمة.

كسر

يتم كتابة الكسر\(\dfrac{a}{b}\)، حيث\(b≠0\)، و a هو البسط\(b\) وهو المقام. يمثل الكسر أجزاء من الكل.

القاسم المشترك الأصغر

القاسم المشترك الأصغر (LCD) لكسرين هو المضاعف المشترك الأصغر (LCM) لمقاساتهما.

عداد

في الكسر المكتوب\(\dfrac{a}{b}\)\(b≠0\)، حيث يشير البسط a إلى عدد الأجزاء المضمنة.

المعاملة بالمثل

يُوجد مقلوب الكسر بقلب الكسر، ووضع البسط في المقام والمقام في البسط.