5.1: בוזונים ופרמיונים

שני אלקטרונים בבאר חד ממדית

עד כה השתמשנו במשוואת שרדינגר כדי לראות כיצד חלקיק בודד, בדרך כלל אלקטרון, מתנהג במגוון פוטנציאלים. אם אנו הולכים לחשוב על אטומים שאינם מימן, יש צורך להרחיב את משוואת שרדינגר כך שתתאר יותר מחלקיק אחד.

כדוגמה פשוטה למערכת של שני חלקיקים, הבה נבחן שני אלקטרונים המוגבלים לאותה באר מרובעת אינסופית חד ממדית,

\[ \begin{matrix} V(x) = 0,& -L/2 < x < L/2\\ V(x) = \infty & otherwise. \end{matrix} \label{5.1.1}\]

כדי להפוך את הדברים לפשוטים עוד יותר, נניח שהאלקטרונים אינם מתקשרים זה עם זה - אנו מכבים את הדחייה האלקטרוסטטית שלהם. ואז באנלוגיה לבניית משוואת שרדינגר לאלקטרון בודד, נוכל לבנות את האנלוגי הדו-אלקטרונים:

\[ -\dfrac{\hbar^2}{2m}\dfrac{\partial^2\Psi(x_1,x_2,t)}{\partial x_1^2}-\dfrac{\hbar^2}{2m}\dfrac{\partial^2\Psi(x_1,x_2,t)}{\partial x_2^2}= E\Psi(x_1,x_2,t) \label{5.1.2}\]

בתוך הבאר, כאשר פונקציית הגל הולכת לאפס עבור \(x_1\) או \(x_2\) שווה ל- \(L/2\) או\(-L/2\).

במבט על משוואה\ ref {5.1.2}, אנו רואים שהיא זהה למשוואת שרדינגר עבור אלקטרון בודד בבאר ריבועית דו מימדית, וכך ניתן לפתור אותה באותו אופן, על ידי הפרדת משתנים. לדוגמה, פונקציית הגל שתכננו עבור הבאר המלבנית הדו-ממדית היא במקרה המרובע:

\[ \Psi_{(2,3)}(x_1,x_2,t)=A\sin \left( \dfrac{2\pi x_1}{L} \right)\cos \left( \dfrac{3\pi x_2}{L} \right)e^{-iEt/\hbar} \label{5.1.3}\]

יש את אותה אנרגיה

\[ E=\dfrac{\hbar^2}{2m}\dfrac{\pi^2}{L^2} \left(2^2+3^2 \right) \label{5.1.4}\]

כפונקציית הגל המובחנת פיזית:

\[ \Psi_{(3,2)}(x_1,x_2,t)=A\sin \left(\dfrac{2\pi x_2}{L} \right)\cos \left( \dfrac{3\pi x_1}{L} \right)e^{-iEt/\hbar} \label{5.1.5}\]

פירוש פונקציית הגל

כבר דנו כיצד יש לפרש את פונקציות הגל לעיל אם הן נחשבות כפונקציות גל דו-ממדיות עבור אלקטרון בודד: \(|\Psi(x_1,x_2)|^2 dx_1dx_2\) היא ההסתברות למצוא את האלקטרון בשטח קטן ב. \(dx_1dx_2\) \((x_1,\, x_2)\)

ההרחבה הטבעית של פרשנות זו לשני אלקטרונים היא להניח כעת \(|\Psi(x_1,\,x_2)|^2 dx_1dx_2\) היא ההסתברות המשותפת למצוא אלקטרון 1 באורך \(dx_1\) קו קטן במיקום\(x_1\), ובמקביל למצוא אלקטרון 2 באורך קטן \(dx_2\) ב\(x_2\).

זה, עם זאת, מוביל לבעיה אמיתית. שקול \(\ref{5.1.3}\) שוב את פונקציית הגל במשוואה. תן לנו עכשיו לקחת נקודות ספציפיות,\(x_1 = 0,\; x_2= L/4\). אז ההסתברות למצוא אלקטרון 1 במרווח אינסופי ב \(x_1\) ואלקטרון 2 באופן דומה ב \(x_2\) הוא אפס, כי \(\Psi\) הוא אפס ב. \(x_1= 0\) מצד שני, ההסתברות למצוא אלקטרון 2 ב \(x_1= 0\) ואלקטרון 1 ב \(x_2 = L/4\) אינה אפס.

הבעיה היא זו: האלקטרונים זהים (אנו מניחים שהסיבובים שלהם מצביעים באותה צורה). אנחנו לא יכולים לדעת איזה הוא, ואף אחד אחר לא יכול. אי ההבחנה בין חלקיקים אלמנטריים אינה דומה לזו של עצמים מקרוסקופיים זהים לכאורה, שבהם תמיד אפשר להציב סימן זעיר כלשהו. אין דרך לסמן אלקטרון. עם זאת, המשמעות היא שהטוב ביותר שאנו יכולים לעשות הוא לדבר על ההסתברות למצוא אלקטרון אחד ב \(x_1\) - \(x_2\), איננו יכולים לציין באיזה אלקטרון אנו מוצאים היכן. לכן, כל פונקציית גל לכאורה שנותנת הסתברויות שונות למציאת אלקטרון 1 ב\(x_1\), 2 ב \(x_2\) ומציאת 2 ב\(x_1\), 1 ב \(x_2\) אינה משמעותית פיזית.

אנו יכולים לנסח את ההסתברות למצוא אלקטרון אחד ב- \(x_1\) ואחר ב-\(x_2\), אך איננו יכולים לציין איזה אלקטרון ספציפי אנו מוצאים בשני המיקומים.

כלומר, פונקציית גל המתארת שני חלקיקים זהים חייבת להיות בעלת התפלגות הסתברות סימטרית

\[ |\Psi(x_1,x_2)|^2=|\Psi(x_2,x_1)|^2 \label{5.1.6}\]

זה בהחלט לא המקרה עם הפונקציה שלנו\(\Psi_{(2,3)}(x_1,x_2)\), כך שלמרות שזה פיתרון למשוואת שרדינגר של שני החלקיקים (משוואה\(\ref{5.1.2}\)), היא אינה פונקציית גל בעלת משמעות פיזית לשני חלקיקים בקופסה.

למעשה, זה לא קשה לתקן - זכרו שלפונקציה \(\Psi_{(3,2)}(x_1,x_2)\) יש אותה אנרגיה, ולמעשה רק תואמת את שני החלקיקים המוחלפים, כלומר:

\[\Psi_{(3,2)}(x_1,x_2)=\Psi_{(2,3)}(x_2,x_1).\]

מכאן נובע כי הפונקציה הסימטרית

\[ \Psi_{(2,3)}^S(x_1,x_2)=\dfrac{1}{\sqrt{2}}(\Psi_{(2,3)}(x_1,x_2) + \Psi_{(2,3)}(x_2,x_1)) \label{5.1.7A}\]

והפונקציה האנטי-סימטרית

\[ \Psi_{(2,3)}^A(x_1,x_2)=\dfrac{1}{\sqrt{2}}(\Psi_{(2,3)}(x_1,x_2) - \Psi_{(2,3)}(x_2,x_1)) \label{5.1.7B}\]

שניהם פתרונות למשוואת שרדינגר לאנרגיה\(E\), ושניהם מספקים את הדרישה \(|\Psi(x_1,x_2)|^2=|\Psi(x_2,x_1)|^2\) הדרושה לחלקיקים זהים, ולכן אלו הן פונקציות הגל המתאימות לשני החלקיקים בתיבה החד-ממדית.

בוזונים, פרמיונים ועקרון ההדרה של פאולי

מתברר שתפקודי גל סימטריים וגם אנטי-סימטריים מתעוררים בטבע בתיאור חלקיקים זהים. למעשה, כל החלקיקים היסודיים הם פרמיונים, בעלי פונקציות גל רב-חלקיקים אנטי-סימטריות, או בוזונים, בעלי פונקציות גל סימטריות. אלקטרונים, פרוטונים ונויטרונים הם פרמיונים; פוטונים, חלקיקי a ואטומי הליום הם בוזונים.

חשוב להבין כי לדרישה זו של סימטריה של התפלגות ההסתברות, הנובעת מחוסר ההבחנה האמיתי של החלקיקים, יש השפעה רבה על התפלגות ההסתברות, ויתרה מכך, ההשפעה שונה מאוד עבור פרמיונים ובוזונים. הדרך הפשוטה ביותר לראות זאת היא רק \(|\Psi(x_1,x_2)|^2\) לשרטט את הסימטרי ולפונקציות הגל האנטי-סימטריות, ולהשוות ביניהן.

במקרה הסימטרי, התפלגות ההסתברות (לא מנורמלת) נראית כך:

(דמות גווני האפור היא מפת קווי מתאר.)

הנקודה העיקרית שיש לציין כאן היא שההסתברות המשותפת הגבוהה ביותר היא זו של מציאת שני החלקיקים קרובים זה לזה, ליד (1,1) ו- (4,4). (נקודות בפועל אלה תלויות כמובן בתפקוד הגל שבחרנו בתחילה).

עכשיו תסתכל על המקרה האנטי-סימטרי:

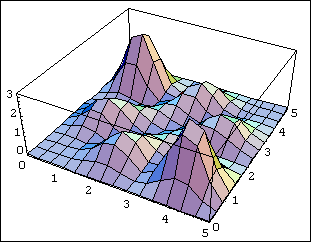
ההבדל הוא דרמטי. עבור פונקציית הגל האנטי-סימטרית, סביר להניח שהחלקיקים יימצאו רחוקים זה מזה. למעשה, יש אפס סבירות שהם יימצאו באותה נקודה, כי אם\(\Psi(x_1,x_2)=-\Psi(x_2,x_1)\), ברור\(\Psi(x,x)=0\). אמירה כללית יותר היא ששני פרמיונים אינם יכולים להיות באותו מצב קוונטי, מכיוון שאם הם היו, פונקציית הגל הייתה בצורה הסימטרית\(f(x_1)f(x_2)\), ולא ניתן היה לבצע אותה נגד סימטריה. זהו עקרון ההדרה של פאולי - זהו הבסיס לטבלה המחזורית, וכתוצאה מכך כמעט לכל דבר אחר.

עקרון ההדרה של פאולי

שני פרמיונים לא יכולים להיות באותו מצב קוונטי (כלומר, אותה קבוצה של מספרים קוונטיים רלוונטיים).

עלינו אולי להדגיש שתפקודי הגל הללו חושבו עם הדחייה האלקטרוסטטית בין האלקטרונים כבויים. זה לא מה שמרחיק את האלקטרונים, אם כי זה יגדיל את ההפרדה אם הוא כלול. עלינו להזהיר גם מפני תמונה קלאסית פשוטה של עקרון פאולי, המחשבה ששני דברים לא יכולים להיות באותו מקום, אחרי הכל, אז אולי אין זה מפתיע ששני אלקטרונים לא יכולים להיות באותו מצב. שני אלקטרונים יכולים להיות באותה פונקציית גל חלל זהה בתנאי שהסיבובים שלהם מצביעים בדרכים הפוכות. יתר על כן, שני בוזונים יכולים להיות באותו מצב, ולמרות שזה אולי נשמע סביר לפוטונים, זה נכון באותה מידה לגבי אטומים כבדים. בעיבוי בוז-איינשטיין, מספר רב של אטומים תופסים את אותו מצב קוונטי. זה קורה בנוזל ⁴ הליום מתחת לשני קלווין בערך, הוא הופך לנוזל-על וזורם ללא חיכוך. עיבוי BE הושג גם עם אוספים מקוררים בלייזר של אטומים גדולים במלכודת.