Skip to main content
Global

2.2: קביעת גובה העץ

  1. Last updated
  2. Save as PDF
  • Page ID
    208243

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    רוב יישומי היער משתמשים באחד משני סוגים של מדידות גובה עצים:

    1. גובה כולל. הגובה הכולל הוא גובה העץ מהגדם שלו ועד קצהו (איור 2.1). גדם של רגל אחת הוא סטנדרטי, אם כי ישנם מקרים בהם משתמשים בבסיס אחר.

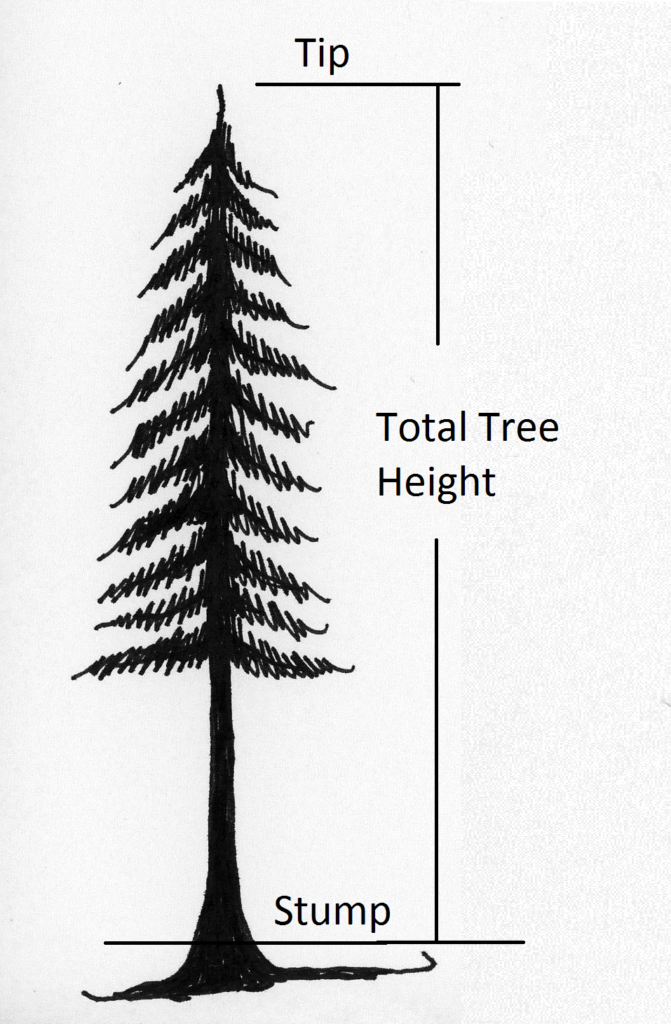
    איור 2.1. גובה העץ הכולל, נמדד מגדם של מטר אחד.

    2. גובה סחיר. גובה סחיר הוא גובה העץ מהגדם שלו לקוטר שבו הגזע קטן מכדי להיות סחיר (איור 2.2). קוטר "עליון סחיר" זה הוא בדרך כלל 6" או אחוז כלשהו מקוטר נמוך בעץ, כגון dbh (ראה פרק 3). "גובה ההתחדדות" דומה מאוד, מבלי שהדגש על הקוטר העליון הוא סוף הסחירות.

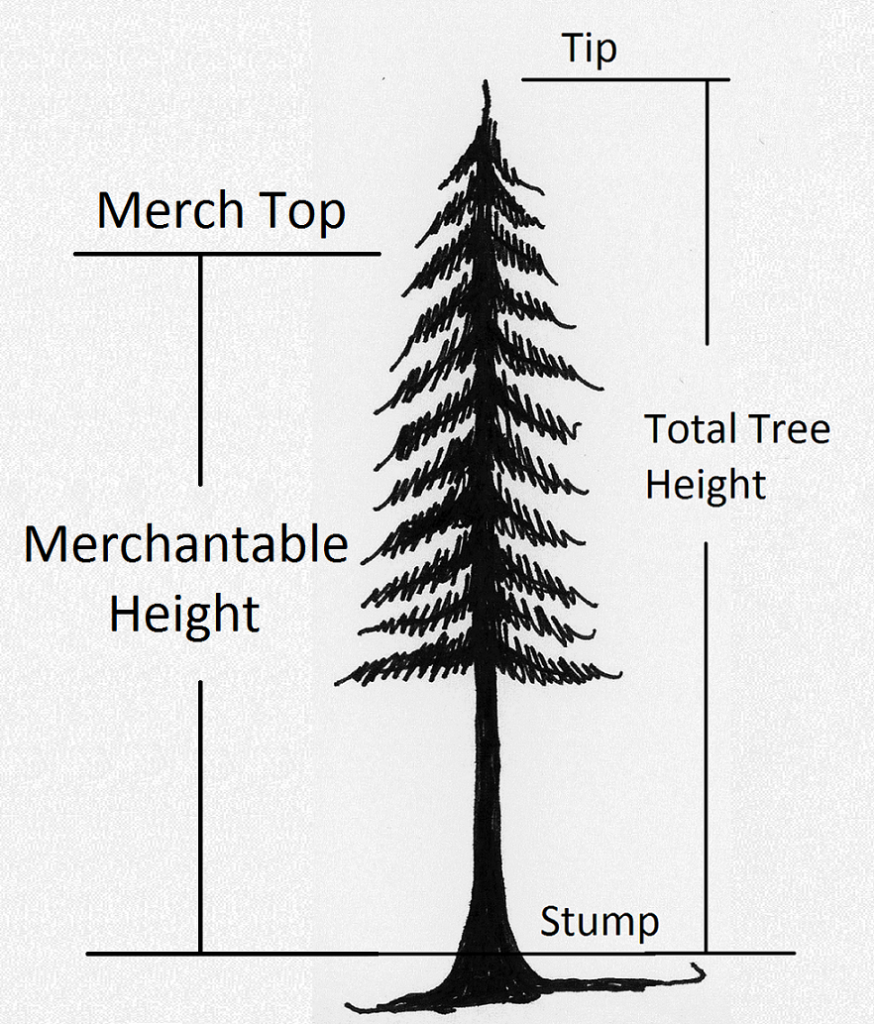
    איור 2.2. גובה סחיר הוא הגובה מהגדם לקוטר הגזע שבו כבר לא ניתן לחתוך את העץ לבולי עץ למכירה.

    העקרונות והטכניקות למדידת כל אחד מהגבהים הללו זהים במהותם. נתמקד בגובה הכולל בטקסט זה.

    אז איך לכל הרוחות אנחנו מבינים כמה גבוה העץ? אין ספק שאנחנו לא מטפסים על כל עץ עם סרט או חותכים כל עץ כדי למדוד אותו. אנו זקוקים לדרך פשוטה, פשוטה ומהירה למדוד את גובה העץ כדי להפוך אותו לחלק אפשרי מנתוני המלאי שלנו. הנה הדרך הקלה ביותר לדיוק טוב:

    בקביעת גובה העץ, אנו מניחים שהעץ מאונך לקרקע. לכן, העץ עושה זווית ישרה עם הקרקע, משולש ימין ניתן למשוך ממנו. שלושת הצדדים של המשולש הם: 1) העץ, 2) המרחק האופקי לאורך הקרקע, ו- 3) קו אלכסוני דמיוני העובר מראש העץ לקרקע. באופן דומה, גובה העץ יכול להיחשב כעלייה ומרחק הקרקע האופקי בריצה. (נשמע מוכר?) אם נוכל למדוד מרחק אופקי מהעץ למקום בו נוכל לראות את ראש העץ, נוכל לקבוע את גובה העץ באמצעות %שיפוע (איור 2.3).

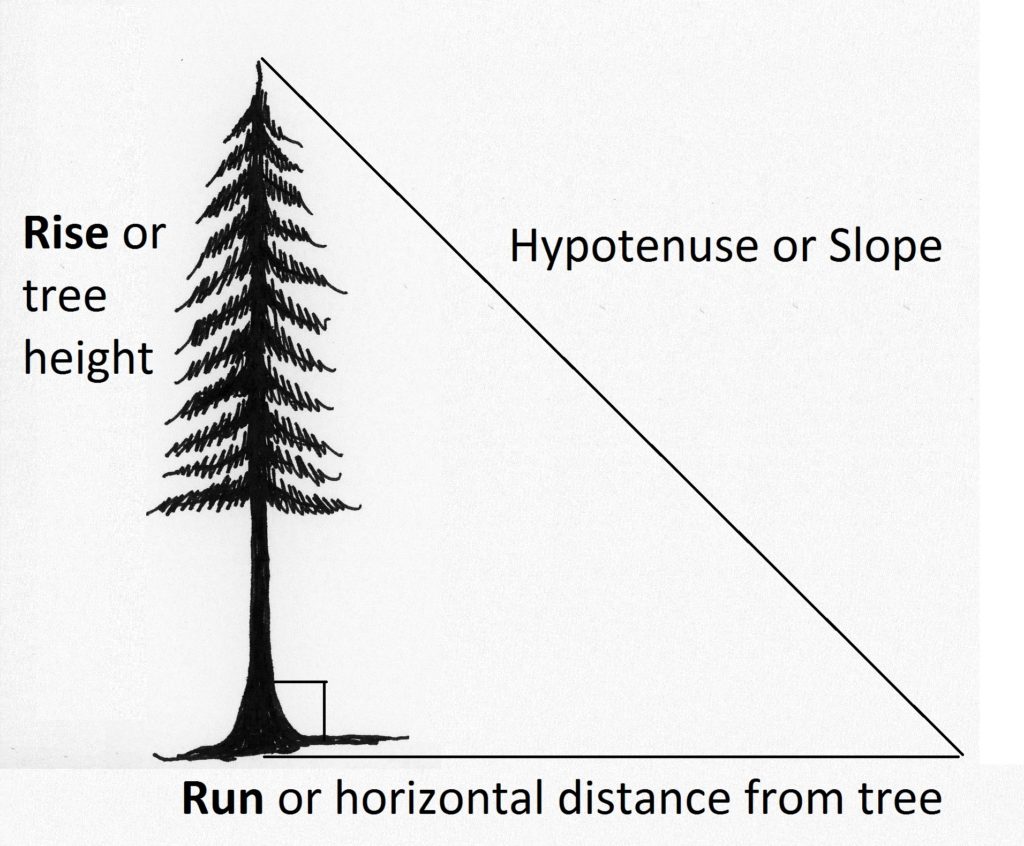
    איור 2.3. עץ עושה זווית ישרה עם הקרקע, כך משולש או מדרון ניתן לצייר באמצעות אותו ואת הקרקע.