9.6: לפתור משוואות עם שורשים מרובעים
- Page ID
- 205502
בסוף פרק זה, תוכל:
- לפתור משוואות רדיקליות
- השתמש בשורשים מרובעים ביישומים
לפני שתתחיל, קח את חידון המוכנות הזה.
- פשט: ⓐ \(\sqrt{9}\) ⓑ\(9^2\).
אם פספסת בעיה זו, עיין בדוגמה 9.1.1 ותרגיל 1.3.22. - לפתור: 5 (איקס+1) -4 = 3 (2איקס−7).
אם פספסת בעיה זו, עיין בתרגיל 2.4.16. - לפתור:\(n^2−6n+8=0\).
אם פספסת בעיה זו, עיין בתרגיל 7.6.13.
לפתור משוואות רדיקליות
בחלק זה נפתור משוואות שיש להן את המשתנה ברדיקנד של שורש ריבועי. משוואות מסוג זה נקראות משוואות רדיקליות.
משוואה שבה המשתנה נמצא ברדיקנד של שורש ריבועי נקראת משוואה רדיקלית.
כרגיל, בפתרון המשוואות הללו, מה שאנחנו עושים לצד אחד של המשוואה עלינו לעשות גם לצד השני. מכיוון שריבוע כמות ולקיחת שורש ריבועי הם פעולות 'הפוכות', אנו מרובעים את שני הצדדים על מנת להסיר את הסימן הרדיקלי ולפתור עבור המשתנה שבפנים.
אך זכרו שכאשר אנו כותבים \(\sqrt{a}\) אנו מתכוונים לשורש הריבועי העיקרי. אז \(\sqrt{a} \ge 0\) תמיד. כאשר אנו פותרים משוואות רדיקליות על ידי ריבוע שני הצדדים אנו עשויים לקבל פתרון אלגברי שיהפוך לשלילי. \(\sqrt{a}\) פתרון אלגברי זה לא יהווה פיתרון למשוואה הרדיקלית המקורית; זהו פיתרון זר. ראינו פתרונות זרים גם כשפתרנו משוואות רציונליות.
למשוואה\(\sqrt{x+2}=x\):
- האם x = 2 הוא פתרון?
- האם x=−1 הוא פתרון?
- תשובה
-
1. האם x = 2 הוא פתרון?
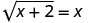
תן x = 2. 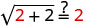
לפשט. 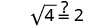
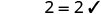
2 זה פתרון. 2. האם x=−1 הוא פתרון?
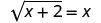
תן איקס = -1. 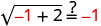
לפשט. 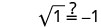
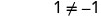
1 זה לא פתרון. -1 הוא פתרון זר למשוואה.
למשוואה\(\sqrt{x+6}=x\):
- האם x=−2 הוא פתרון?
- האם x=3 הוא פתרון?
- תשובה
-
- לא
- כן
למשוואה\(\sqrt{−x+2}=x\):
- האם x=−2 הוא פתרון?
- האם x = 1 הוא פתרון?
- תשובה
-
- לא
- כן
עבור\(a \ge 0\), \((\sqrt{a})^2=a\)
כיצד לפתור משוואות רדיקליות
לפתור: \(\sqrt{2x−1}=7\)
- תשובה
-
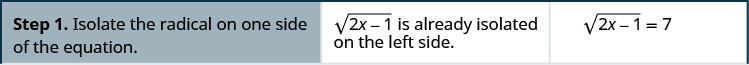



לפתור:\(\sqrt{3x−5}=5\).
- תשובה
-
10
לפתור:\(\sqrt{4x+8}=6\).
- תשובה
-
7
- לבודד את הרדיקל בצד אחד של המשוואה.
- מרובע את שני צידי המשוואה.
- לפתור את המשוואה החדשה.
- בדוק את התשובה.
לפתור:\(\sqrt{5n−4}−9=0\).
- תשובה
-
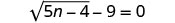
כדי לבודד את הרדיקל, הוסף 9 לשני הצדדים. 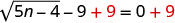
לפשט. 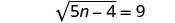
מרובע את שני צידי המשוואה. 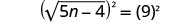
לפתור את המשוואה החדשה. 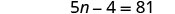


בדוק את התשובה.

הפתרון הוא n = 17.
לפתור:\(\sqrt{3m+2}−5=0\).
- תשובה
-
\(\frac{23}{3}\)
לפתור:\(\sqrt{10z+1}−2=0\).
- תשובה
-
\(\frac{3}{10}\)
לפתור:\(\sqrt{3y+5}+2=5\).
- תשובה
-
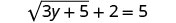
כדי לבודד את הרדיקל, לחסר 2 משני הצדדים. 
לפשט. 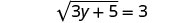
מרובע את שני צידי המשוואה. 
לפתור את המשוואה החדשה. 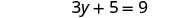

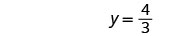
בדוק את התשובה.
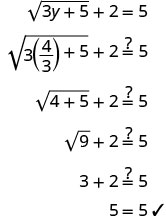
הפתרון הוא \(y=\frac{4}{3}\)
לפתור:\(\sqrt{3p+3}+3=5\).
- תשובה
-
\(\frac{1}{3}\)
לפתור:\(\sqrt{5q+1}+4=6\).
- תשובה
-
\(\frac{3}{5}\)
כאשר אנו משתמשים בסימן רדיקלי, אנו מתכוונים לשורש העיקרי או החיובי. אם למשוואה יש שורש ריבועי השווה למספר שלילי, למשוואה זו לא יהיה פיתרון.
לפתור:\(\sqrt{9k−2}+1=0\).
- תשובה
-
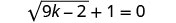
כדי לבודד את הרדיקל, לחסר 1 משני הצדדים. 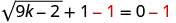
לפשט. 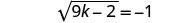
מכיוון שהשורש הריבועי שווה למספר שלילי, למשוואה אין פיתרון.
לפתור: \(\sqrt{2r−3}+5=0\)
- תשובה
-
אין פתרון
לפתור:\(\sqrt{7s−3}+2=0\).
- תשובה
-
אין פתרון
\[\begin{array}{cc} {(a+b)^2=a^2+2ab+b^2}&{(a−b)^2=a^2−2ab+b^2}\\ \nonumber \end{array}\]
אל תשכח את טווח הביניים!
לפתור:\(\sqrt{p−1}+1=p\).
- תשובה
-
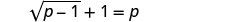
כדי לבודד את הרדיקל, לחסר 1 משני הצדדים. 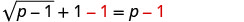
לפשט. 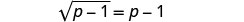
מרובע את שני צידי המשוואה. 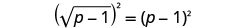
פשט ואז פתר את המשוואה החדשה. 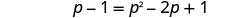
זו משוואה ריבועית, אז קבל אפס בצד אחד. 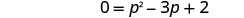
פקטור בצד ימין. 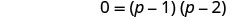
השתמש במאפיין המוצר אפס. 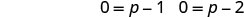
לפתור כל משוואה. 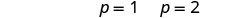
בדוק את התשובות.
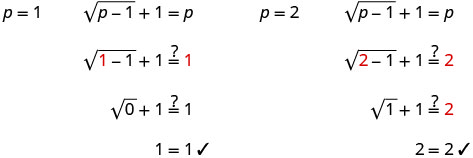
הפתרונות הם p = 1, p = 2.
לפתור:\(\sqrt{x−2}+2=x\).
- תשובה
-
2, 3
לפתור:\(\sqrt{y−5}+5=y\).
- תשובה
-
5, 6
לפתור:\(\sqrt{r+4}−r+2=0\).
- תשובה
-
\(\sqrt{r+4}−r+2=0\) לבודד את הרדיקל. \(\sqrt{r+4}=r−2\) מרובע את שני צידי המשוואה. \((\sqrt{r+4})^2=(r−2)^2\) לפתור את המשוואה החדשה. \(r+4=r^2−4r+4\) זו משוואה ריבועית, אז קבל אפס בצד אחד. \(0=r^2−5r\) פקטור בצד ימין. \(0=r(r−5)\) השתמש במאפיין המוצר אפס. 0=ר 0=ר−5 לפתור את המשוואה. ר=0 ר=5 בדוק את התשובה.
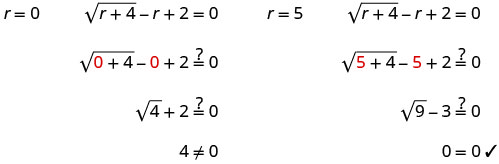
ר=5 r=0 הוא פתרון חיצוני.
לפתור:\(\sqrt{m+9}−m+3=0\).
- תשובה
-
7
לפתור: \(\sqrt{n+1}−n+1=0\)
- תשובה
-
3
כשיש מקדם מול הרדיקל, עלינו לרבע אותו גם כן.
לפתור:\(3\sqrt{3x−5}−8=4\).
- תשובה
-
\(3\sqrt{3x−5}−8=4\) לבודד את הרדיקל. \(3\sqrt{3x−5}=12\) מרובע את שני צידי המשוואה. \((3\sqrt{3x−5})^2=(12)^2\) פשט ואז פתר את המשוואה החדשה. 9 (3איקס−5) =144 להפיץ. 27איקס-45=144 לפתור את המשוואה. 27איקס=189 איקס=7 בדוק את התשובה.
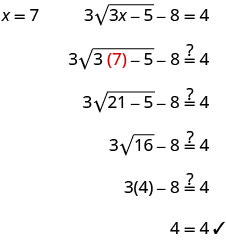
הפתרון הוא x = 7.
לפתור:\(\sqrt{24a+2}−16=16\).
- תשובה
-
\(\frac{127}{2}\)
לפתור:\(\sqrt{36b+3}−25=50\).
- תשובה
-
\(\frac{311}{3}\)
לפתור:\(\sqrt{4z−3}=\sqrt{3z+2}\).
- תשובה
-
\(\sqrt{4z−3}=\sqrt{3z+2}\) המונחים הרדיקליים מבודדים \(\sqrt{4z−3}=\sqrt{3z+2}\) מרובע את שני צידי המשוואה. \((\sqrt{4z−3})^2=(\sqrt{3z+2})^2\) פשט ואז פתר את המשוואה החדשה 4 ז-3 = 3 ז+2 ז-3 = 2 z=5 איקס=7 בדוק את התשובה.
אנו משאירים לך להראות ש -5 צ'קים!
הפתרון הוא z=5.
לפתור:\(\sqrt{2x−5}=\sqrt{5x+3}\).
- תשובה
-
אין פתרון
לפתור:\(\sqrt{7y+1}=\sqrt{2y−5}\).
- תשובה
-
אין פתרון
לפעמים לאחר ריבוע שני צידי המשוואה, עדיין יש לנו משתנה בתוך רדיקל. כשזה קורה, אנו חוזרים על שלב 1 ושלב 2 בהליך שלנו. אנו מבודדים שוב את הרדיקל והמרובע משני צידי המשוואה.
לפתור:\(\sqrt{m}+1=\sqrt{m+9}\).
- תשובה
-
\(\sqrt{m}+1=\sqrt{m+9}\) הרדיקל בצד ימין מבודד.
מרובע את שני הצדדים
\((\sqrt{m}+1)^2=(\sqrt{m+9})^2\) פשוט - היזהר מאוד כשאתה מכפיל! \(m+2\sqrt{m}+1=m+9\) יש עדיין רדיקל במשוואה.
אז עלינו לחזור על הצעדים הקודמים. לבודד את הרדיקל.
\(2\sqrt{m}=8\) מרובע משני הצדדים. \((2\sqrt{m})^2=(8)^2\) פשט ואז פתר את המשוואה החדשה. 4 מ '= 64 מ = 16 בדוק את התשובה.
אנו משאירים לך להראות ש- m = 16 צ'קים!
הפתרון הוא M = 16.
לפתור:\(\sqrt{x}+3=\sqrt{x+5}\).
- תשובה
-
אין פתרון
לפתור:\(\sqrt{m}+5=\sqrt{m+16}\).
- תשובה
-
אין פתרון
לפתור:\(\sqrt{q−2}+3=\sqrt{4q+1}\).
- תשובה
-
\(\sqrt{q−2}+3=\sqrt{4q+1}\) הרדיקל בצד ימין מבודד.
מרובע את שני הצדדים
\((\sqrt{q−2}+3)^2=(\sqrt{4q+1})^2\) לפשט. \(q−2+6\sqrt{q−2}+9=4q+1\) יש עדיין רדיקל במשוואה.
אז עלינו לחזור על הצעדים הקודמים. לבודד את הרדיקל.
\(6\sqrt{q−2}=3q−6\) מרובע משני הצדדים. \((6\sqrt{q−2})^2=(3q−6)^2\) פשט ואז פתר את המשוואה החדשה. \(36(q−2)=9q^2−36q+36\) להפיץ. \(36q−72=9q^2−36q+36\) זו משוואה ריבועית, אז קבל אפס בצד אחד. \(0=9q^2−72q+108\) פקטור בצד ימין. \(0=9(q^2−8q+12)\)
\(0=9(q−6)(q−2)\)
השתמש במאפיין מוצר אפס \[\begin{array}{ll} {q−6=0}&{q−2=0}\\ {q=6}&{q=2}\\ \nonumber \end{array}\] ההמחאות נשארות לך. (שני הפתרונות צריכים לעבוד.)
הפתרונות הם q = 6 ו- q = 2.
לפתור:\(\sqrt{y−3}+2=\sqrt{4y+2}\).
- תשובה
-
אין פתרון
לפתור:\(\sqrt{n−4}+5=\sqrt{3n+3}\).
- תשובה
-
אין פתרון
השתמש בשורשים מרובעים ביישומים
ככל שתתקדם בקורסי המכללה שלך, תיתקל בנוסחאות הכוללות שורשים מרובעים בתחומים רבים. כבר השתמשנו בנוסחאות כדי לפתור יישומי גיאומטריה.
אנו נשתמש באסטרטגיית פתרון הבעיות שלנו ליישומי גיאומטריה, עם שינויים קלים, כדי לתת לנו תוכנית לפיתרון יישומים עם נוסחאות מכל תחום.
- קרא את הבעיה וודא שכל המילים והרעיונות מובנים. במידת הצורך, צייר דמות ותייג אותה במידע הנתון.
- זהה את מה שאנחנו מחפשים.
- תן שם למה שאנחנו מחפשים על ידי בחירת משתנה שייצג אותו.
- תרגם למשוואה על ידי כתיבת הנוסחה או המודל המתאימים למצב. תחליף במידע הנתון.
- לפתור את המשוואה באמצעות טכניקות אלגברה טובות.
- בדוק את התשובה בבעיה וודא שהיא הגיונית.
- ענה על השאלה במשפט שלם.
השתמשנו בנוסחה A = L · W כדי למצוא את השטח של מלבן עם אורך L ורוחב W. ריבוע הוא מלבן בו האורך והרוחב שווים. אם אנו נותנים ל - s להיות באורך של צד של ריבוע, שטח הריבוע הוא \(s^2\).
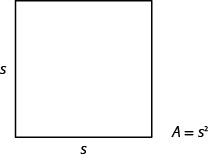
הנוסחה \(A=s^2\) נותנת לנו את שטח הריבוע אם אנו יודעים את אורך הצד. מה אם נרצה למצוא את אורך הצד לאזור נתון? אז אנחנו צריכים לפתור את המשוואה עבור s.
\[\begin{array}{ll} {}&{A=s^2}\\ {\text{Take the square root of both sides.}}&{\sqrt{A}=\sqrt{s^2}}\\ {\text{Simplify.}}&{s=\sqrt{A}}\\ \nonumber \end{array}\]
אנו יכולים להשתמש בנוסחה \(s=\sqrt{A}\) כדי למצוא את אורך הצד של ריבוע לאזור נתון.
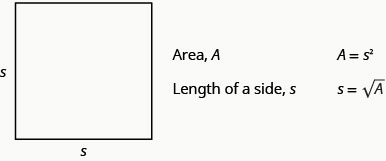
נציג דוגמה לכך בדוגמה הבאה.
מייק ולישל רוצים ליצור פטיו מרובע. יש להם מספיק בטון כדי לסלול שטח של 200 מטרים רבועים. השתמש בנוסחה \(s=\sqrt{A}\) כדי למצוא את אורך כל צד של הפטיו. עגול את תשובתך לעשירית הרגל הקרובה ביותר.
- תשובה
-
שלב 1. קרא את הבעיה. צייר דמות
ותייג אותה במידע הנתון.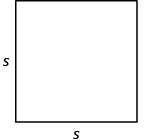
A = 200 מטרים רבועים שלב 2. זהה את מה שאתה מחפש. אורכו של צד הפטיו המרובע. שלב 3. תן שם למה שאתה מחפש על ידי
בחירת משתנה שייצג אותו.בואו s = אורך הצד. שלב 4. תרגם למשוואה על ידי כתיבת הנוסחה או המודל
המתאימים למצב.
החלף את המידע הנתון.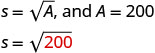
שלב 5. לפתור את המשוואה באמצעות
טכניקות אלגברה טובות. עגול למקום עשרוני אחד.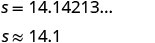
שלב 6. בדוק את התשובה בבעיה
וודא שהיא הגיונית.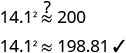
זה קרוב מספיק מכיוון שעיגלנו את השורש
הריבועי.
האם פטיו עם צד 14.1 רגל סביר?
כן.שלב 7. ענה על השאלה
במשפט שלם.כל צד של הפטיו צריך להיות 14.1 רגל.
קייטי רוצה לשתול מדשאה מרובעת בחצר הקדמית שלה. יש לה מספיק סודה כדי לכסות שטח של 370 מטרים רבועים. השתמש בנוסחה \(s=\sqrt{A}\) כדי למצוא את אורך כל צד של הדשא שלה. עגול את תשובתך לעשירית הרגל הקרובה ביותר.
- תשובה
-
19.2 רגל
סרחיו רוצה להכין פסיפס מרובע כשיבוץ לשולחן שהוא בונה. יש לו מספיק אריח כדי לכסות שטח של 2704 סנטימטרים רבועים. השתמש בנוסחה \(s=\sqrt{A}\) כדי למצוא את אורך כל צד של הפסיפס שלו. עגול את תשובתך לעשירית הרגל הקרובה ביותר.
- תשובה
-
52.0 סמ"
יישום נוסף של שורשים מרובעים קשור לכוח המשיכה.
על כדור הארץ, אם אובייקט נשמט מגובה של מטר שעה, הזמן בשניות שייקח להגיע לקרקע נמצא באמצעות הנוסחה,
\(t=\frac{\sqrt{h}}{4}\)
לדוגמה, אם אובייקט נשמט מגובה של 64 רגל, נוכל למצוא את הזמן שלוקח להגיע לקרקע על ידי החלפת h = 64 בנוסחה.
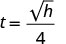 |
|
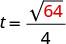 |
|
| קח את השורש הריבועי של 64. | 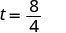 |
| פשט את השבר. | 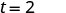 |
ייקח 2 שניות עד שחפץ שנפל מגובה 64 רגל יגיע לקרקע.
כריסטי הפילה את משקפי השמש שלה מגשר 400 מטר מעל נהר. השתמש בנוסחה \(t=\frac{\sqrt{h}}{4}\) כדי למצוא כמה שניות לקח למשקפי השמש להגיע לנהר.
- תשובה
-
שלב 1. קרא את הבעיה. שלב 2. זהה את מה שאתה מחפש. הזמן שלוקח למשקפי השמש להגיע
לנהר.שלב 3. תן שם למה שאתה מחפש על ידי
בחירת משתנה שייצג אותו.תן t = זמן. שלב 4. תרגם למשוואה על ידי כתיבת הנוסחה או המודל
המתאימים למצב.
תחליף במידע הנתון.

שלב 5. לפתור את המשוואה באמצעות
טכניקות אלגברה טובות.

שלב 6. בדוק את התשובה בבעיה
וודא שהיא הגיונית.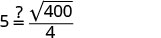

5=5 ✓האם חמש שניות נראות הגיוניות?
כן.שלב 7. ענה על השאלה
במשפט שלם.ייקח 5 שניות עד שמשקפי השמש יפגעו
במים.
מסוק הפיל חבילת הצלה מגובה 1,296 רגל. השתמש בנוסחה \(t=\frac{\sqrt{h}}{4}\) כדי למצוא כמה שניות לקח לחבילה להגיע לקרקע.
- תשובה
-
9 שניות
מכונת כביסה לחלונות הפילה מגב מרציף 196 רגל מעל המדרכה השתמש בנוסחה \(t=\frac{\sqrt{h}}{4}\) כדי למצוא כמה שניות לקח למגב להגיע למדרכה.
- תשובה
-
3.5 שניות
שוטרים החוקרים תאונות דרכים מודדים את אורך סימני ההחלקה על המדרכה. ואז הם משתמשים בשורשים מרובעים כדי לקבוע את המהירות, במיילים לשעה, מכונית נסעה לפני הפעלת הבלמים.
אם אורך סימני ההחלקה הוא d רגל, ניתן למצוא את המהירות, s, של המכונית לפני הפעלת הבלמים באמצעות הנוסחה,
\(s=\sqrt{24d}\)
לאחר תאונת דרכים, סימני ההחלקה של מכונית אחת נמדדו 190 רגל. השתמש בנוסחה \(s=\sqrt{24d}\) כדי למצוא את מהירות המכונית לפני הפעלת הבלמים. עגול את תשובתך לעשירית הקרובה ביותר.
- תשובה
-
שלב 1. קרא את הבעיה. שלב 2. זהה את מה שאנחנו מחפשים. מהירות של מכונית. שלב 3. תן שם למה שאנחנו מחפשים. בואו s = המהירות. שלב 4. תרגם למשוואה על ידי כתיבת הנוסחה המתאימה. 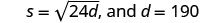
החלף את המידע הנתון. 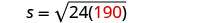
שלב 5. לפתור את המשוואה. 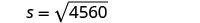
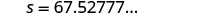
סיבוב למקום עשרוני אחד. 
שלב 6. בדוק את התשובה בבעיה.
67.5 ≈? 24 (190) √ 67.5≈?
4560 √ 67.5≈?
67.5277...האם 67.5 קמ"ש היא מהירות סבירה? כן. שלב 7. ענה על השאלה במשפט שלם. מהירות המכונית הייתה כ -67.5 מייל לשעה.
חוקר תאונות מדד את סימני ההחלקה של המכונית. אורך סימני ההחלקה היה 76 רגל. השתמש בנוסחה \(s=\sqrt{24d}\) כדי למצוא את מהירות המכונית לפני הפעלת הבלמים. עגול את תשובתך לעשירית הקרובה ביותר.
- תשובה
-
42.7 רגל
סימני ההחלקה של רכב שהיה מעורב בתאונה היו באורך 122 רגל. השתמש בנוסחה \(s=\sqrt{24d}\) כדי למצוא את מהירות הרכב לפני הפעלת הבלמים. עגול את תשובתך לעשירית הקרובה ביותר.
- תשובה
-
54.1 רגל
מושגי מפתח
- כדי לפתור משוואה רדיקלית:
- לבודד את הרדיקל בצד אחד של המשוואה.
- מרובע את שני צידי המשוואה.
- לפתור את המשוואה החדשה.
- בדוק את התשובה. ייתכן שחלק מהפתרונות שהושגו לא יעבדו במשוואה המקורית.
- פתרון יישומים עם נוסחאות
- קרא את הבעיה וודא שכל המילים והרעיונות מובנים. במידת הצורך, צייר דמות ותייג אותה במידע הנתון.
- זהה את מה שאנחנו מחפשים.
- תן שם למה שאנחנו מחפשים על ידי בחירת משתנה שייצג אותו.
- תרגם למשוואה על ידי כתיבת הנוסחה או המודל המתאימים למצב. תחליף במידע הנתון.
- לפתור את המשוואה באמצעות טכניקות אלגברה טובות.
- בדוק את התשובה בבעיה וודא שהיא הגיונית.
- ענה על השאלה במשפט שלם.
- שטח של ריבוע
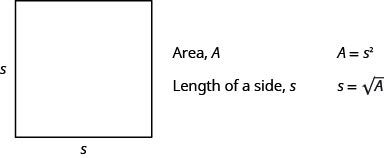
- חפצים נופלים
- על כדור הארץ, אם אובייקט נשמט מגובה של מטר שעה, הזמן בשניות שייקח להגיע לקרקע נמצא באמצעות הנוסחה\(t=\frac{\sqrt{h}}{4}\).
- סימני החלקה ומהירות של מכונית
- אם אורך סימני ההחלקה הוא d רגל, ניתן למצוא את המהירות, s, של המכונית לפני הפעלת הבלמים באמצעות הנוסחה\(s=\sqrt{24d}\).
רשימת מילים
- משוואה רדיקלית
- משוואה שבה המשתנה נמצא ברדיקנד של שורש ריבועי נקראת משוואה רדיקלית


