9.1: פשט והשתמש בשורשים מרובעים
- Page ID
- 205489
בסוף פרק זה, תוכל:
- פשט ביטויים עם שורשים מרובעים
- הערכת שורשים מרובעים
- שורשים מרובעים משוערים
- פשט ביטויים משתנים עם שורשים מרובעים
לפני שתתחיל, קח את חידון המוכנות הזה.
פשט ביטויים עם שורשים מרובעים
זכור שכאשר מספר n מוכפל בעצמו, אנו כותבים \(n^2\) וקוראים אותו "n בריבוע". לדוגמה, \(15^2\) נקרא "15 בריבוע", ו 225 נקרא ריבוע של 15, מאז\(15^2=225\).
אם\(n^2=m\), אז m הוא הריבוע של n.
לפעמים נצטרך להסתכל על הקשר בין מספרים לריבועים שלהם הפוך. מכיוון ש- 225 הוא הריבוע של 15, אנו יכולים גם לומר ש- 15 הוא שורש ריבועי של 225. מספר שהריבוע שלו הוא m נקרא שורש ריבועי של m.
אם\(n^2=m\), אז n הוא שורש ריבועי של m.
שימו לב \((−15)^2=225\) also, so −15 is also a square root of 225. Therefore, both 15 and −15 are square roots of 225.
לכן, לכל מספר חיובי יש שני שורשים מרובעים - אחד חיובי ואחד שלילי. מה אם היינו רוצים רק את השורש הריבועי החיובי של מספר חיובי? הסימן הרדיקלי,\(\sqrt{m}\), מציין את השורש הריבועי החיובי. השורש הריבועי החיובי נקרא גם השורש הריבועי העיקרי.
אנו משתמשים גם בסימן הרדיקלי לשורש הריבועי של אפס. כי\(0^2=0\),\(\sqrt{0}=0\). שימו לב שלאפס יש רק שורש ריבועי אחד.
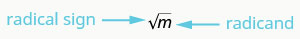
\(\sqrt{m}\)נקרא "השורש הריבועי של m."
אם\(m=n^2\), אז\(\sqrt{m}=n\), עבור\(n \ge 0\).
השורש הריבועי של m,\(\sqrt{m}\), הוא המספר החיובי שהריבוע שלו הוא m.
מכיוון ש- 15 הוא השורש הריבועי החיובי של 225, אנו כותבים \(\sqrt{225}=15\). Fill in איור להכנת טבלה של שורשים מרובעים שתוכלו להתייחס אליהם תוך כדי עבודה בפרק זה.

אנו יודעים שלכל מספר חיובי יש שני שורשים מרובעים והסימן הרדיקלי מציין את החיובי. אנחנו כותבים\(\sqrt{225}=15\). אם אנו רוצים למצוא את השורש הריבועי השלילי של מספר, אנו מציבים שלילי מול הסימן הרדיקלי. לדוגמה,\(−\sqrt{225}=−15\).
פשט:
- \(\sqrt{36}\)
- \(\sqrt{196}\)
- \(−\sqrt{81}\)
- \(−\sqrt{289}\).
- תשובה
-
1.
\[\begin{array}{ll} {}&{\sqrt{36}}\\ {\text{Since} 6^2=36}&{6}\\ \end{array}\]
2.
\[\begin{array}{ll} {}&{\sqrt{196}}\\ {\text{Since} 14^2=196}&{14}\\ \end{array}\]
3.
\[\begin{array}{ll} {}&{−\sqrt{81}}\\ {\text{The negative is in front of the radical sign}}&{−9}\\ \end{array}\]
4.
\[\begin{array}{ll} {}&{−\sqrt{289}}\\ {\text{The negative is in front of the radical sign}}&{−17}\\ \end{array}\]
פשט:
- \(−\sqrt{49}\)
- \(\sqrt{225}\).
- תשובה
-
- −7
- 15
לרמוז:
- \(\sqrt{64}\)
- \(−\sqrt{121}\).
- תשובה
-
- 8
- −11
פשט:
- \(\sqrt{−169}\)
- \( −\sqrt{64}\)
- תשובה
-
1.
\[\begin{array}{ll} {}&{\sqrt{−169}}\\ {\text{There is no real number whose square is} s−169}&{\sqrt{−169} \text{is not a real number.}}\\ \end{array}\]
2.\[\begin{array}{ll} {}&{−\sqrt{64}}\\ {\text{The negative is in front of the radical sign}}&{−8}\\ \end{array}\]
פשט:
- \(\sqrt{−196}\)
- \(−\sqrt{81}\).
- תשובה
-
- לא מספר אמיתי
- −9
פשט:
- \(−\sqrt{49}\)
- \(\sqrt{ −121}\).
- תשובה
-
- −7
- לא מספר אמיתי
כאשר משתמשים בסדר הפעולות כדי לפשט ביטוי שיש לו שורשים מרובעים, אנו מתייחסים לרדיקל כאל סמל קיבוץ.
פשט:
- \(\sqrt{25} +\sqrt{144}\)
- \(\sqrt{25+144}\).
- תשובה
-
1.
\[\begin{array}{ll} {}&{\sqrt{25} +\sqrt{144}}\\ {\text{Use the order of operations}}&{5+12}\\ {\text{Simplify.}}&{17}\\ \end{array}\]
2.\[\begin{array}{ll} {}&{\sqrt{25+144}}\\ {\text{Simplify under the radical sign.}}&{\sqrt{169}}\\ {\text{Simplify.}}&{13}\\ \end{array}\]
שימו לב לתשובות השונות בחלקים 1 ו -2!
פשט:
- \(\sqrt{9}+\sqrt{16}\)
- \(\sqrt{9+16}\).
- תשובה
-
- 7
- 5
פשט:
- \(\sqrt{64+225}\)
- \(\sqrt{64}+\sqrt{225}\).
- תשובה
-
- 17
- 23
הערכת שורשים מרובעים
עד כה שקלנו רק שורשים מרובעים של מספרים מרובעים מושלמים. השורשים הריבועיים של מספרים אחרים אינם מספרים שלמים. תסתכל על הטבלה למטה.
| מספר | שורש מרובע |
|---|---|
| 4 | \(\sqrt{4}=2\) |
| 5 | \(\sqrt{5}\) |
| 6 | \(\sqrt{6}\) |
| 7 | \(\sqrt{7}\) |
| 8 | \(\sqrt{8}\) |
| 9 | \(\sqrt{9}=3\) |
השורשים הריבועיים של המספרים בין 4 ל -9 חייבים להיות בין שני המספרים השלמים ברציפות 2 ו -3, והם אינם מספרים שלמים. בהתבסס על התבנית בטבלה לעיל, נוכל לומר כי \(\sqrt{5}\) חייב להיות בין 2 ל 3. בעזרת סמלי אי-שוויון אנו כותבים:
\(2<\sqrt{5}<3\)
הערכה \(\sqrt{60}\) בין שני מספרים שלמים רצופים.
- תשובה
-
חשבו על המספרים המרובעים המושלמים הקרובים ביותר ל -60. הכינו שולחן קטן מהריבועים המושלמים הללו ושורשי הריבועים שלהם.
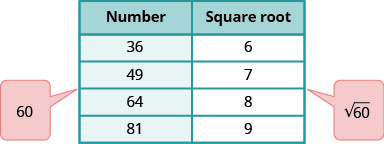
אתר 60 בין שני ריבועים מושלמים רצופים. 
\(\sqrt{60}\)הוא בין השורשים הריבועיים שלהם. 
הערך את השורש הריבועי \(\sqrt{38}\) בין שני מספרים שלמים רצופים.
- תשובה
-
\(6<\sqrt{38}<7\)
הערך את השורש הריבועי \(\sqrt{84}\) בין שני מספרים שלמים רצופים.
- תשובה
-
\(9<\sqrt{84}<10\)
שורשים מרובעים משוערים
ישנן שיטות מתמטיות לקירוב שורשים מרובעים, אך כיום רוב האנשים משתמשים במחשבון כדי למצוא אותם. מצא את \(\sqrt{x}\) המפתח במחשבון שלך. תשתמש במפתח זה כדי להעריך שורשים מרובעים.
כשאתה משתמש במחשבון שלך כדי למצוא את השורש הריבועי של מספר שאינו ריבוע מושלם, התשובה שאתה רואה אינה השורש הריבועי המדויק. זהו קירוב, מדויק למספר הספרות המוצגות בתצוגת המחשבון שלך. הסמל לקירוב הוא \(\approx\) והוא נקרא 'בערך'.
נניח שלמחשבון שלך יש תצוגה בת 10 ספרות. היית רואה את זה
\(\sqrt{5} \approx 2.236067978\)
אם היינו רוצים \(\sqrt{5}\) לעגל לשני מקומות עשרוניים, היינו אומרים
\(\sqrt{5} \approx 2.24\)
כיצד נדע שערכים אלה הם קירובים ולא הערכים המדויקים? תראו מה קורה כשאנחנו מרובעים אותם:
\[\begin{array}{c} {(2.236067978)^2=5.000000002}\\ {(2.24)^2=5.0176}\\ \end{array}\]
הריבועים שלהם קרובים ל -5, אך אינם שווים בדיוק ל -5.
בעזרת מקש השורש הריבועי במחשבון ואז עיגול לשני מקומות עשרוניים, אנו יכולים למצוא:
\[\begin{array}{c} {\sqrt{4}=2}\\ {\sqrt{5} \approx 2.24}\\ {\sqrt{6} \approx 2.45}\\ {\sqrt{7} \approx 2.65}\\ {\sqrt{8} \approx 2.83}\\ {\sqrt{9}=3}\\ \end{array}\]
עגול \(\sqrt{17}\) לשני מקומות אחרי הנקודה העשרונית.
- תשובה
-
\[\begin{array}{ll} {}&{\sqrt{17}}\\ {\text{Use the calculator square root key.}}&{4.123105626...}\\ {\text{Round to two decimal places.}}&{4.12}\\ {}&{\sqrt{17} \approx 4.12} \end{array}\]
עגול \(\sqrt{11}\) לשני מקומות אחרי הנקודה העשרונית.
- תשובה
-
\(\approx 3.32\)
עגול \(\sqrt{13}\) לשני מקומות אחרי הנקודה העשרונית.
- תשובה
-
\(\approx 3.61\)
פשט ביטויים משתנים עם שורשים מרובעים
מה אם נצטרך למצוא שורש ריבועי של ביטוי עם משתנה? שקול\(\sqrt{9x^2}\). האם אתה יכול לחשוב על ביטוי שהריבוע שלו הוא\(9x^2\)?
\[\begin{array}{cc} {(?)^2=9x^2}&{}\\ {(3x)^2=9x^2}&{\text{so} \sqrt{9x^2}=3x}\\ \end{array}\]
כאשר אנו משתמשים בסימן הרדיקלי כדי לקחת את השורש הריבועי של ביטוי משתנה, עלינו לציין כי x≥0x≥0 כדי לוודא שנקבל את השורש הריבועי העיקרי.
עם זאת, בפרק זה נניח שכל משתנה בביטוי שורש מרובע מייצג מספר לא שלילי ולכן לא נכתוב \(x \ge 0\) ליד כל רדיקל.
מה לגבי שורשים מרובעים של כוחות משתנים גבוהים יותר? חשבו על תכונת הכוח של אקספונסנטים בהם השתמשנו בפרק 6.
\((a^m)^n=a^{m·n}\)
אם נתייצב\(a^m\), המעריך יהפוך ל -2 מטר.
\((a^m)^2=a^{2m}\)
איך זה עוזר לנו לקחת שורשים מרובעים? בואו נסתכל על כמה:
\[\begin{array}{cc} {\sqrt{25u^8}=5u^4}&{\text{Because} (5u^4)^2=25u^8}\\ {\sqrt{16r^{20}}=4r^{10}}&{\text{Because} (4r^{10})^2=16r^{20}}\\ {\sqrt{196q^{36}}=14q^{18}}&{\text{Because} (14r^{18})^2=196q^{36}}\\ \end{array}\]
פשט:
- \(\sqrt{x^6}\)
- \(\sqrt{y^{16}}\)
- תשובה
-
1.
\[\begin{array}{ll} {}&{\sqrt{x^6}}\\ {\text{Since} (x^3)^2=x^6}&{x^3}\\ \end{array}\]
2.\[\begin{array}{ll} {}&{\sqrt{y^{16}}}\\ {\text{Since} (y^8)^2=y^{16}}&{y^8}\\ \end{array}\]
פשט:
- \(\sqrt{y^8}\)
- \(\sqrt{z^{12}}\).
- תשובה
-
- \(y^4\)
- \(z^6\)
פשט:
- \(\sqrt{m^4}\)
- \(\sqrt{b^{10}}\).
- תשובה
-
- \(m^2\)
- \(b^5\)
פשט: \(\sqrt{16n^2}\)
- תשובה
-
\[\begin{array}{ll} {}&{\sqrt{16n^2}}\\ {\text{Since} (4n)^2=16n^2}&{4n}\\ \end{array}\]
פשט:\(\sqrt{64x^2}\).
- תשובה
-
\(8x\)
פשט:\(\sqrt{169y^2}\).
- תשובה
-
\(13y\)
פשט:\(−\sqrt{81c^2}\).
- תשובה
-
\[\begin{array}{ll} {}&{−\sqrt{81c^2}}\\ {\text{Since} (9c)^2=81c^2}&{−9c}\\ \end{array}\]
פשט:\(−\sqrt{121y^2}\).
- תשובה
-
\(−11y\)
פשט:\(−\sqrt{100p^2}\).
- תשובה
-
\(−10p\)
פשט:\(\sqrt{36x^{2}y^{2}}\).
- תשובה
-
\[\begin{array}{ll} {}&{\sqrt{36x^{2}y^{2}}}\\ {\text{Since} (6xy)^2=\sqrt{36x^{2}y^{2}}}&{6xy}\\ \end{array}\]
פשט:\(\sqrt{100a^{2}b^{2}}\).
- תשובה
-
10ab
פשט:\(\sqrt{225m^{2}n^{2}}\).
- תשובה
-
15 דקות
פשט:\(\sqrt{64p^{64}}\).
- תשובה
-
\[\begin{array}{ll} {}&{\sqrt{64p^{64}}}\\ {\text{Since} (8p^8)^2=\sqrt{64p^{64}}}&{8p^8}\\ \end{array}\]
פשט:\(\sqrt{49x^{30}}\).
- תשובה
-
\(7x^{15}\)
פשט: \(\sqrt{81w^{36}}\)
- תשובה
-
\(9w^{18}\)
פשט: \(\sqrt{121a^{6}b^{8}}\)
- תשובה
-
\[\begin{array}{ll} {}&{\sqrt{121a^{6}b^{8}}}\\ {\text{Since} (11a^{3}b^{4})^2=\sqrt{121a^{6}b^{8}}}&{11a^{3}b^{4}}\\ \end{array}\]
פשט: \(\sqrt{169x^{10}y^{14}}\)
- תשובה
-
\(13x^{5}y^{7}\)
פשט: \(\sqrt{144p^{12}q^{20}}\)
- תשובה
-
\(\sqrt{12p^{6}q^{10}}\)
גש למשאב מקוון זה לקבלת הדרכה ותרגול נוספים עם שורשים מרובעים.
- שורשים מרובעים
מושגי מפתח
- שים לב שהשורש הריבועי של מספר שלילי אינו מספר ממשי.
- לכל מספר חיובי יש שני שורשים מרובעים, אחד חיובי ואחד שלילי. השורש הריבועי החיובי של מספר חיובי הוא השורש הריבועי העיקרי.
- אנו יכולים להעריך שורשים מרובעים באמצעות ריבועים מושלמים סמוכים.
- אנו יכולים להעריך שורשים מרובעים באמצעות מחשבון.
- כאשר אנו משתמשים בסימן הרדיקלי כדי לקחת את השורש הריבועי של ביטוי משתנה, עלינו לציין זאת \(x \ge 0\) כדי לוודא שאנו מקבלים את השורש הריבועי העיקרי.
רשימת מילים
- ריבוע של מספר
-
- אם\(n^2=m\), אז m הוא הריבוע של n
- שורש ריבועי של מספר
-
- אם\(n^2=m\), אז n הוא שורש ריבועי של m
- סימון שורש ריבועי
-
- אם\(m=n^2\), אז\(\sqrt{m}=n\). אנו קוראים \(\sqrt{m}\) בשם "השורש הריבועי של m."


