Skip to main content
Global

8.9: השתמש בווריאציה ישירה והפוכה

  1. Last updated
  2. Save as PDF
  • Page ID
    205478

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    מטרות למידה

    בסוף פרק זה, תוכל:

    • לפתור בעיות וריאציה ישירה
    • לפתור בעיות וריאציה הפוכות
    הערה

    לפני שתתחיל, קח את חידון המוכנות הזה.

    אם אתה מפספס בעיה, חזור לסעיף המפורט ובדוק את החומר.

    1. מצא את ההופכי הכפל של -8
      אם פספסת בעיה זו, עיין בתרגיל 1.10.13.
    2. פתור עבור n: 45 = 20n
      אם פספסת בעיה זו, עיין בתרגיל 2.2.1.
    3. הערך \(5x^2\) מתי x = 10
      אם פספסת בעיה זו, עיין בתרגיל 1.3.25.

    כאשר שתי כמויות קשורות בפרופורציה, אנו אומרים שהן פרופורציונליות זו לזו. דרך נוספת לבטא קשר זה היא לדבר על השונות של שני הכמויות. נדון בשונות ישירה ובשונות הפוכה בחלק זה.

    לפתור בעיות וריאציה ישירה

    לינדזי מקבלת 15 דולר לשעה בעבודתה. אם ניתן s להיות המשכורת שלה ו h להיות מספר השעות שהיא עבדה, נוכל לדגמן את המצב הזה עם המשוואה

    s = 15 שעות

    המשכורת של לינדזי היא תוצר של קבוע, 15, ומספר השעות שהיא עובדת. אנו אומרים כי המשכורת של לינדזי משתנה ישירות עם מספר השעות שהיא עובדת. שני משתנים משתנים ישירות אם האחד הוא תוצר של קבוע והשני.

    הגדרה: וריאציה ישירה

    עבור כל שני משתנים x ו- y, y משתנה ישירות עם x אם

    y = קאיקס, איפה \(n \ne 0\)

    ביישומים המשתמשים בווריאציה ישירה, בדרך כלל נדע ערכים של זוג אחד מהמשתנים ונתבקש למצוא את המשוואה המתייחסת ל - x ו- y. אז נוכל להשתמש במשוואה זו כדי למצוא ערכים של y לערכים אחרים של x.

    כיצד לפתור בעיות וריאציה ישירה

    דוגמא \(\PageIndex{1}\)

    אם y משתנה ישירות עם x ו- y = 20 כאשר x = 8, מצא את המשוואה המתייחסת ל- x ו- y.

    תשובה

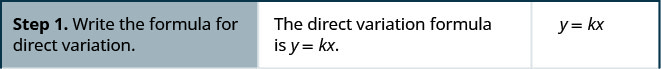
    התמונה לעיל כוללת 3 עמודות. הטבלה מציגה את השלבים לפתרון בעיות וריאציה ישירה. שלב ראשון הוא לכתוב את הנוסחה עבור וריאציה ישירה. נוסחת הווריאציה הישירה היא y שווה k x ואז נקבל y שווה k כפול x.שלב שני הוא להחליף את הערכים הנתונים עבור המשתנים. אנו מקבלים y שווה 20 ו x שווה 8. אז יש לנו 20 שווה k פעמים 8.שלב שלישי הוא לפתור את השונות המתמדת. חלקו את שני צידי המשוואה ב- 8 ואז הכפלו. עכשיו אנחנו מקבלים 20 מחולק על ידי 8 שווה ק ק שווה 2.5.שלב רביעי הוא לכתוב את המשוואה המתייחסת ל- x ו- y כתוב מחדש את המשוואה הכללית עם הערך שמצאנו k כדי לקבל y שווה 2 וחמש עשיריות פעמים x.

    דוגמא \(\PageIndex{2}\)

    אם y משתנה ישירות כ- x ו- y = 3, כאשר x = 10, מצא את המשוואה המתייחסת ל- x ו- y.

    תשובה

    \(y=\frac{3}{10}x\)

    דוגמא \(\PageIndex{3}\)

    אם y משתנה ישירות כ- x ו- y = 12 כאשר x = 4, מצא את המשוואה המתייחסת ל- x ו- y.

    תשובה

    y = 3x

    נפרט את השלבים הבאים.

    הגדרה: לפתור בעיות וריאציה ישירה
    1. כתוב את הנוסחה לשינוי ישיר.
    2. החלף את הערכים הנתונים עבור המשתנים.
    3. לפתור את קבוע השונות.
    4. כתוב את המשוואה המתייחסת ל- x ו- y.

    עכשיו נפתור כמה יישומים של וריאציה ישירה.

    דוגמא \(\PageIndex{4}\)

    כאשר ראול רץ על ההליכון בחדר הכושר, מספר הקלוריות, ג, הוא שורף משתנה ישירות עם מספר הדקות, מ ', הוא משתמש בהליכון. הוא שרף 315 קלוריות כשהשתמש בהליכון במשך 18 דקות.

    1. כתוב את המשוואה המתייחסת ל- c ו- m.
    2. כמה קלוריות הוא היה שורף אם היה רץ על ההליכון במשך 25 דקות?
    תשובה

    1.

      מספר הקלוריות, c משתנה ישירות עם מספר הדקות, m, על ההליכון ו- c = 315 כאשר m = 18
    כתוב את הנוסחה לשינוי ישיר. .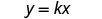
    אנו נשתמש ב- c במקום y ו- mm במקום x. .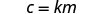
    החלף את הערכים הנתונים עבור המשתנים. .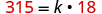
    לפתור את קבוע השונות. .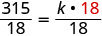
      .
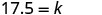
    כתוב את המשוואה המתייחסת ל- c ו- m. .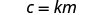
    תחליף בקבוע השונות. .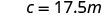

    2.

     

    מצא את c כאשר m = 25.
    כתוב את המשוואה המתייחסת ל- c ו- m. .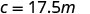
    החלף את הערך הנתון עבור m. .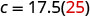
    לפשט. .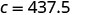
      ראול היה שורף 437.5 קלוריות אם היה משתמש בהליכון במשך 25 דקות.
    דוגמא \(\PageIndex{5}\)

    מספר הקלוריות, c, נשרף משתנה ישירות עם כמות הזמן, t, בילה פעילות גופנית. ארנולד שרף 312 קלוריות תוך 65 דקות פעילות גופנית.

    1. כתוב את המשוואה המתייחסת ל- c ו - t.
    2. כמה קלוריות הוא היה שורף אם הוא מתאמן במשך 90 דקות?
    תשובה
    1. c=4.8 ט
    2. 432 קלוריות
    דוגמא \(\PageIndex{6}\)

    המרחק שגוף נע נע, ד, משתנה ישירות עם הזמן, t, הוא נע. רכבת נוסעת 100 מייל תוך שעתיים

    1. כתוב את המשוואה המתייחסת ל- d ו - t.
    2. כמה קילומטרים זה יעבור בחמש שעות?
    תשובה
    1. ד=50 ט
    2. 250 מיילים

    בדוגמה הקודמת, המשתנים c ו - m נקראו בבעיה. בדרך כלל זה לא המקרה. נצטרך לתת שם למשתנים בדוגמה הבאה כחלק מהפתרון, בדיוק כמו שאנחנו עושים ברוב הבעיות המיושמות.

    דוגמא \(\PageIndex{7}\)

    מספר גלוני הדלק שמכוניתה של יוניס משתמשת משתנה ישירות עם מספר הקילומטרים שהיא נוהגת. בשבוע שעבר היא נסעה 469.8 קילומטרים והשתמשה 14.5 ליטרים של גז.

    1. כתוב את המשוואה המתייחסת למספר גלונים של גז המשמש למספר הקילומטרים המונעים.
    2. בכמה גלונים של דלק המכונית של יוניס תשתמש אם היא נסעה 1000 מייל?
    תשובה

    1.

      מספר גלוני הגז משתנה ישירות עם מספר הקילומטרים שנסעו.
    ראשית נקרא את המשתנים. תן g = מספר גלונים של גז.
    m = מספר קילומטרים שנסעו.
    כתוב את הנוסחה לשינוי ישיר. .
    נשתמש ב- g במקום y ו- m במקום x. .
    החלף את הערכים הנתונים עבור המשתנים .
      .
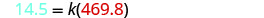
    לפתור את קבוע השונות. .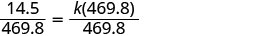
    נסתובב לאלף הקרוב ביותר. .
    כתוב את המשוואה המתייחסת ל- g ו- m. .
    תחליף בקבוע השונות. .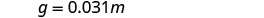

    2.

      מצא g כאשר m = 1000.
    כתוב את המשוואה המתייחסת ל- g ו- m. ז=0.031 מ '
    החלף את הערך הנתון עבור m. ז=0.031 (1000)
    לפשט. ז=31
      המכונית של יוניס תשתמש ב-31 ליטרים של דלק אם היא תנהג בה 1,000 מייל.

    שימו לב שבדוגמה זו היחידות על קבוע השונות הן גלונים/מייל. בחיי היומיום, אנחנו בדרך כלל מדברים על מיילים/גלון.

    דוגמא \(\PageIndex{8}\)

    המרחק שבראד נוסע משתנה ישירות עם זמן הנסיעה. בראד נסע 660 קילומטרים תוך 12 שעות,

    1. כתוב את המשוואה המתייחסת למספר הקילומטרים שנסעו לזמן.
    2. כמה קילומטרים יכול בראד לנסוע בארבע שעות?
    תשובה
    1. מ = 55 שעות
    2. 220 מיילים
    דוגמא \(\PageIndex{9}\)

    משקלו של נוזל משתנה ישירות כנפחו. נוזל שמשקלו 24 פאונד הוא בעל נפח של 4 ליטר.

    1. כתוב את המשוואה המתייחסת למשקל לנפח.
    2. אם לנוזל יש נפח 13 ליטר, מה משקלו?
    תשובה
    1. w = 6 וולט
    2. 78 פאונד

    במצבים מסוימים, משתנה אחד משתנה ישירות עם הריבוע של המשתנה השני. כשזה קורה, משוואת השונות הישירה היא\(y=kx^2\).

    דוגמא \(\PageIndex{10}\)

    העומס המרבי שקרן תתמוך בו משתנה ישירות עם ריבוע האלכסון של חתך הקורה. קרן עם אלכסון 4" תתמוך בעומס מרבי של 75 פאונד.

    1. כתוב את המשוואה המתייחסת לעומס המרבי לחתך הרוחב.
    2. מהו העומס המרבי שיכול להיות נתמך על ידי קרן עם אלכסון 8 "?
    תשובה

    1.

      העומס המרבי משתנה ישירות עם ריבוע האלכסון של החתך.
    תן שם למשתנים. תן L = עומס מרבי.
    c = האלכסון של החתך
    כתוב את הנוסחה לשינוי ישיר, כאשר y משתנה ישירות עם הריבוע של x. .
    אנו נשתמש ב- L במקום y ו- c במקום x. .
    החלף את הערכים הנתונים עבור המשתנים. .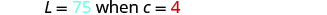
      .
    לפתור את קבוע השונות. .
      .
    כתוב את המשוואה המתייחסת ל ו- c. .
    תחליף בקבוע השונות. .

    2.

      מצא את L כאשר c = 8.
    כתוב את המשוואה המתייחסת ל ו- c. \(L=4.6875c^2\)
    החלף את הערך הנתון עבור ג. \(L=4.6875(8)^2\)
    לפשט. L=300
      קרן עם אלכסון 8" יכול לתמוךעומס מרבי של 300 פאונד.
    דוגמא \(\PageIndex{11}\)

    המרחק שאובייקט נופל הוא ביחס ישר לריבוע הזמן בו הוא נופל. כדור נופל 144 רגל תוך 3 שניות.

    1. כתוב את המשוואה המתייחסת למרחק לזמן.
    2. כמה רחוק חפץ ייפול תוך 4 שניות?
    תשובה
    1. \(d=16t^2\)
    2. 256 רגל
    דוגמא \(\PageIndex{12}\)

    שטח המעגל משתנה ישירות כריבוע הרדיוס. פיצה עגולה ברדיוס של 6 אינץ 'כוללת שטח של 113.04 אינץ' רבוע.

    1. כתוב את המשוואה המתייחסת לאזור לרדיוס.
    2. מה השטח של פיצה ברדיוס של 9 אינץ '?
    תשובה
    1. \(A=3.14r^2\)
    2. 254.34 סנטימטרים רבועים

    לפתור בעיות וריאציה הפוכה

    יישומים רבים כוללים שני משתנים המשתנים הפוך. ככל שמשתנה אחד גדל, השני פוחת. המשוואה שמתייחסת אליהם היא\(y=\frac{k}{x}\).

    הגדרה: וריאציה הפוכה

    עבור כל שני משתנים x ו- y, y משתנה הפוך עם x אם

    y =\(\frac{k}{x}\), איפה \(k \ne 0\)

    המילה 'הפוך' בווריאציה הפוכה מתייחסת להיפוך הכפל. ההופכי הכפול של x הוא. \(\frac{1}{x}\)

    אנו פותרים בעיות שונות הפוכות באותו אופן שבו פתרנו בעיות וריאציה ישירה. רק הצורה הכללית של המשוואה השתנתה. נעתיק את תיבת ההליך כאן ופשוט נשנה את 'ישיר' ל'הפוך '.

    הגדרה: לפתור בעיות וריאציה הפוכות
    1. כתוב את הנוסחה עבור וריאציה הפוכה.
    2. החלף את הערכים הנתונים עבור המשתנים.
    3. לפתור את קבוע השונות.
    4. כתוב את המשוואה המתייחסת ל- x ו- y.
    דוגמא \(\PageIndex{13}\)

    אם y משתנה הפוך עם x ו- y = 20 כאשר x = 8 x ו- y.

    תשובה
    כתוב את הנוסחה עבור וריאציה הפוכה. .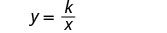
    החלף את הערכים הנתונים עבור המשתנים. .
      .
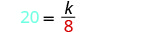
    לפתור את קבוע השונות. .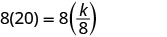
      .
    כתוב את המשוואה המתייחסת ל- x ו- y. .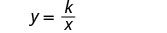
    תחליף בקבוע השונות. .
    דוגמא \(\PageIndex{14}\)

    אם p משתנה הפוך עם q ו- p = 30 כאשר q = 12 מצא את המשוואה המתייחסת p ו- q.

    תשובה

    \(p=\frac{360}{q}\)

    דוגמא \(\PageIndex{15}\)

    אם y משתנה הפוך עם x ו- y = 8 כאשר x = 2 מצא את המשוואה המתייחסת ל- x ו- y.

    תשובה

    \(y=\frac{16}{x}\)

    דוגמא \(\PageIndex{16}\)

    צריכת הדלק (mpg) של מכונית משתנה הפוך עם משקלה. מכונית ששוקלת 3100 פאונד מקבלת 26 מגה פיקסל בכביש המהיר.

    1. כתוב את משוואת הווריאציה.
    2. מה תהיה צריכת הדלק של מכונית ששוקלת 4030 פאונד?
    תשובה

    1.

      צריכת הדלק משתנה הפוך עם המשקל.
    ראשית נקרא את המשתנים. תן f = צריכת דלק.
    w = משקל.
    כתוב את הנוסחה עבור וריאציה הפוכה. .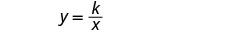
    אנו נשתמש ב- f במקום y ו- w במקום x. .
    החלף את הערכים הנתונים עבור המשתנים. .
      .
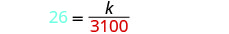
    לפתור את קבוע השונות. .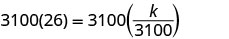
      .
    כתוב את המשוואה המתייחסת f ו- w. .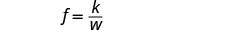
    תחליף בקבוע השונות. .

    2.

      מצא את f כאשר w = 4030.
    כתוב את המשוואה המתייחסת f ו- w. .
    החלף את הערך הנתון עבור w. \(f=\frac{80,600}{4030}\)
    לפשט. f = 20
      מכונית ששוקלת 4030 פאונד תהיה צריכת דלק של 20 מגה פיקסל.
    דוגמא \(\PageIndex{17}\)

    ערך המכונית משתנה ביחס הפוך לגילו. אלנה קנתה מכונית בת שנתיים תמורת 20 אלף דולר.

    1. כתוב את משוואת הווריאציה.
    2. מה יהיה הערך של המכונית של אלנה כשהיא בת 5?
    תשובה
    1. \(v=\frac{40,000}{a}\)
    2. $8,000
    דוגמא \(\PageIndex{18}\)

    הזמן הנדרש לריקון בריכה משתנה הפוך כמו קצב השאיבה. זה לקח לוסי 2.5 שעות לרוקן את הבריכה שלה באמצעות משאבה שדורגה ב 400 gpm (גלונים לדקה).

    1. כתוב את משוואת הווריאציה.
    2. כמה זמן ייקח לה לרוקן את הבריכה באמצעות משאבה המדורגת 500 gpm?
    תשובה
    1. \(t=\frac{1000}{r}\)
    2. 2 שעות
    דוגמא \(\PageIndex{19}\)

    התדירות של מיתר גיטרה משתנה הפוך לאורכו. למחרוזת ארוכה בגודל 26 אינץ 'יש תדר של 440 רעידות בשנייה.

    1. כתוב את משוואת הווריאציה.
    2. כמה רעידות בשנייה יהיו אם אורך המיתר יופחת ל -20 "על ידי הנחת אצבע על סיבוב?
    תשובה

    1.

      התדר משתנה הפוך עם האורך.
    תן שם למשתנים. תן f = תדר.
    L = אורך.
    כתוב את הנוסחה עבור וריאציה הפוכה. .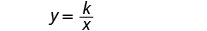
    אנו נשתמש ב- f במקום y ו- L במקום x .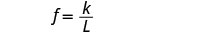
    החלף את הערכים הנתונים עבור המשתנים. .
      .
    לפתור את קבוע השונות. .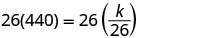
      .
    כתוב את המשוואה המתייחסת f ו- L. .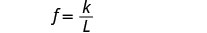
    תחליף בקבוע השונות. .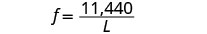

    2.

      מצא f כאשר L = 20.
    כתוב את המשוואה המתייחסת f ו- L. \(f=\frac{11,440}{L}\)
    החלף את הערך הנתון עבור L. \(f=\frac{11,440}{20}\)
    לפשט. ו=572
      למיתר גיטרה בגודל 20 אינץ 'יש תדר 572 רעידות בשנייה.
    דוגמא \(\PageIndex{20}\)

    מספר השעות שלוקח לקרח להמיס משתנה הפוך לטמפרטורת האוויר. נניח גוש קרח נמס תוך שעתיים כשהטמפרטורה היא 65 מעלות.

    1. כתוב את משוואת הווריאציה.
    2. כמה שעות ייקח לאותו גוש קרח להימס אם הטמפרטורה הייתה 78 מעלות?
    תשובה
    1. \(h=\frac{130}{t}\)
    2. \(1\frac{2}{3}\)שעות
    דוגמא \(\PageIndex{21}\)

    הכוח הדרוש לשבירת לוח משתנה הפוך לאורכו. ריצ'רד משתמש בלחץ של 24 קילו כדי לשבור לוח באורך 2 מטר.

    1. כתוב את משוואת הווריאציה.
    2. כמה קילוגרמים של לחץ נדרשים כדי לשבור לוח באורך 5 מטר?
    תשובה
    1. \(F=\frac{48}{L}\)
    2. 9.6 פאונד