8.6: לפתור משוואות רציונליות
- Page ID
- 205484
בסוף פרק זה תוכל:
- לפתור משוואות רציונליות
- לפתור משוואה רציונלית למשתנה ספציפי
לפני שתתחיל, קח את חידון המוכנות הזה.
אם אתה מפספס בעיה, חזור לסעיף המפורט ובדוק את החומר.
- לפתור:\(\frac{1}{6}x+\frac{1}{2}=\frac{1}{3}\).
אם פספסת בעיה זו, עיין בתרגיל 2.5.1. - לפתור:\(n^2−5n−36=0\).
אם פספסת בעיה זו, עיין בתרגיל 7.6.13. - לפתור עבור y במונחים של x: 5x+2y = 10 עבור y.
אם פספסת בעיה זו, עיין בתרגיל 2.6.22.
לאחר הגדרת המונחים ביטוי ומשוואה בשלב מוקדם ביסודות, השתמשנו בהם לאורך ספר זה. פישטנו סוגים רבים של ביטויים ופתרנו סוגים רבים של משוואות. פישטנו ביטויים רציונליים רבים עד כה בפרק זה. עכשיו נפתור משוואות רציונליות.
ההגדרה של משוואה רציונלית דומה להגדרת המשוואה בה השתמשנו ביסודות.
משוואה רציונלית היא שני ביטויים רציונליים המחוברים בסימן שווה.
עליכם להקפיד לדעת את ההבדל בין ביטויים רציונליים למשוואות רציונליות. המשוואה מכילה סימן שווה.
\[\begin{array}{cc} {\textbf{Rational Expression}}&{\textbf{Rational Equation}}\\ {\frac{1}{8}x+\frac{1}{2}}&{\frac{1}{8}x+\frac{1}{2}=\frac{1}{4}}\\ {\frac{y+6}{y^2−36}}&{\frac{y+6}{y^2−36}=y+1}\\ {\frac{1}{n−3}+\frac{1}{n+4}}&{\frac{1}{n−3}+\frac{1}{n+4}=\frac{15}{n^2+n−12}}\\ \nonumber \end{array}\]
לפתור משוואות רציונליות
כבר פתרנו משוואות לינאריות שהכילו שברים. מצאנו את ה- LCD של כל השברים במשוואה ואז הכפלנו את שני צידי המשוואה על ידי ה- LCD כדי "לנקות" את השברים.
הנה דוגמה שעשינו כשעבדנו עם משוואות לינאריות:
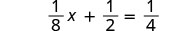 |
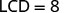 |
|
| הכפלנו את שני הצדדים על ידי ה- LCD. | 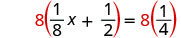 |
|
| ואז חילקנו. | 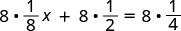 |
|
| פישטנו - ואז הייתה לנו משוואה ללא שברים. | 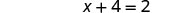 |
|
| לבסוף פתרנו את המשוואה הזו. | 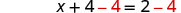 |
|
 |
נשתמש באותה אסטרטגיה כדי לפתור משוואות רציונליות. נכפיל את שני צידי המשוואה על ידי ה- LCD. אז תהיה לנו משוואה שאינה מכילה ביטויים רציונליים ולכן הרבה יותר קל לנו לפתור.
אך מכיוון שלמשוואה המקורית עשוי להיות משתנה במכנה, עלינו להיזהר שלא נגיע לפיתרון שיהפוך מכנה שווה לאפס.
אז לפני שנתחיל לפתור משוואה רציונלית, אנו בוחנים אותה תחילה כדי למצוא את הערכים שיהפכו כל מכנה לאפס. בדרך זו, כאשר נפתור משוואה רציונלית נדע אם יש פתרונות אלגבריים שעלינו להשליך.
פתרון אלגברי למשוואה רציונלית שתגרום לאי-הגדרה של כל אחד מהביטויים הרציונליים נקרא פתרון זר.
פתרון זר למשוואה רציונלית הוא פתרון אלגברי שיגרום לכל אחד מהביטויים במשוואה המקורית להיות בלתי מוגדר.
אנו מציינים כל פתרונות חיצוניים אפשריים, ג, על ידי כתיבה \(x \ne c\) next to the equation.
כיצד לפתור משוואות עם ביטויים רציונליים
לפתור:\(\frac{1}{x}+\frac{1}{3}=\frac{5}{6}\).
- תשובה
-

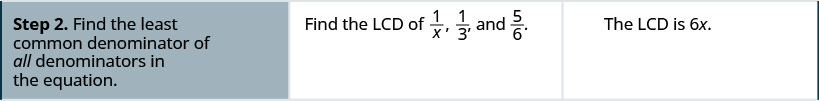



לפתור:\(\frac{1}{y}+\frac{2}{3}=\frac{1}{5}\).
- תשובה
-
\(−\frac{15}{7}\)
לפתור:\(\frac{2}{3}+\frac{1}{5}=\frac{1}{x}\).
- תשובה
-
\(\frac{15}{13}\)
השלבים של שיטה זו מוצגים להלן.
- שימו לב לכל ערך של המשתנה שיהפוך כל מכנה לאפס.
- מצא את המכנה הפחות משותף של כל המכנים במשוואה.
- נקה את השברים על ידי הכפלת שני צידי המשוואה ב- LCD.
- לפתור את המשוואה המתקבלת.
- בדוק.
- אם ערכים כלשהם שנמצאים בשלב 1 הם פתרונות אלגבריים, מחק אותם.
- בדוק את כל הפתרונות שנותרו במשוואה המקורית.
אנו תמיד מתחילים לציין את הערכים שיגרמו לכל מכנה להיות אפס.
לפתור:\(1−\frac{5}{y}=−\frac{6}{y^2}\).
- תשובה
-
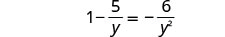
שימו לב לכל ערך של המשתנה שיהפוך כל מכנה לאפס. 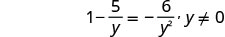
מצא את המכנה הפחות משותף של כל המכנים במשוואה. LCD הוא \(y^2\) נקה את השברים על ידי הכפלת שני צידי המשוואה ב- LCD. 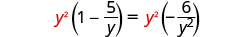
להפיץ. 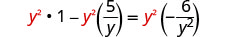
להכפיל. 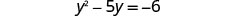
לפתור את המשוואה המתקבלת. ראשית כתוב את המשוואה הריבועית בצורה סטנדרטית. 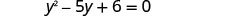
פקטור. 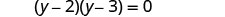
השתמש במאפיין מוצר אפס. 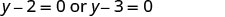
לפתור. 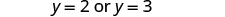
בדוק. לא קיבלנו 0 כפתרון אלגברי. 
לפתור:\(1−\frac{2}{a}=\frac{15}{a^2}\).
- תשובה
-
5, -3
לפתור:\(1−\frac{4}{b}=\frac{12}{b^2}\).
- תשובה
-
6, -2
לפתור:\(\frac{5}{3u−2}=\frac{3}{2u}\).
- תשובה
-
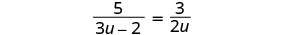
שימו לב לכל ערך של המשתנה שיהפוך כל מכנה לאפס. 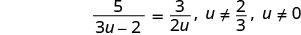
מצא את המכנה הפחות משותף של כל המכנים במשוואה. LCD הוא 2u (3u-2). נקה את השברים על ידי הכפלת שני צידי המשוואה ב- LCD. 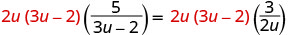
הסר גורמים נפוצים. 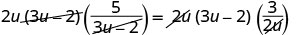
לפשט. 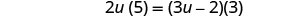
להכפיל. 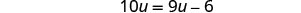
לפתור את המשוואה המתקבלת. 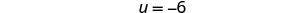
לא קיבלנו 0 או \(\frac{2}{3}\) כפתרונות אלגבריים. 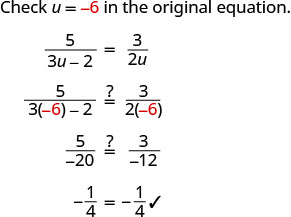
לפתור:\(\frac{1}{x−1}=\frac{2}{3x}\).
- תשובה
-
-2
לפתור:\(\frac{3}{5n+1}=\frac{2}{3n}\).
- תשובה
-
-2
כאשר אחד המכנים הוא ריבועי, זכור לחשב אותו תחילה כדי למצוא את ה- LCD.
לפתור:\(\frac{2}{p+2}+\frac{4}{p−2}=\frac{p−1}{p^2−4}\).
- תשובה
-
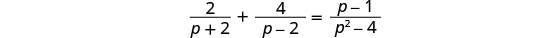
שימו לב לכל ערך של המשתנה שיהפוך כל מכנה לאפס. 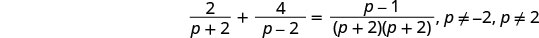
מצא את המכנה הפחות משותף של כל המכנים במשוואה. ה- LCD הוא (p+2) (p −2). נקה את השברים על ידי הכפלת שני צידי המשוואה ב- LCD. 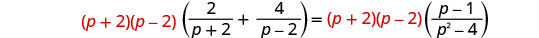
להפיץ. 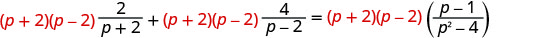
הסר גורמים נפוצים. 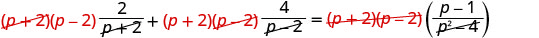
לפשט. 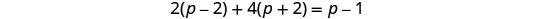
להפיץ. 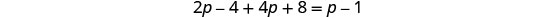
לפתור. 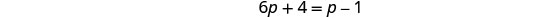


לא קיבלנו 2 או -2 כפתרונות אלגבריים. 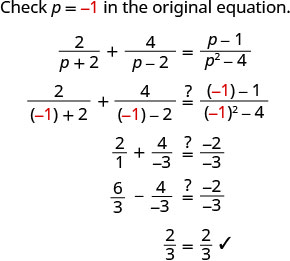
לפתור:\(\frac{2}{x+1}+\frac{1}{x−1}=\frac{1}{x^2−1}\).
- תשובה
-
\(\frac{2}{3}\)
לפתור: \(\frac{5}{y+3}+\frac{2}{y−3}=\frac{5}{y^2−9}\)
- תשובה
-
2
לפתור:\(\frac{4}{q−4}−\frac{3}{q−3}=1\).
- תשובה
-

שימו לב לכל ערך של המשתנה שיהפוך כל מכנה לאפס. 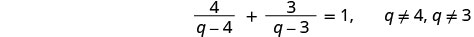
מצא את המכנה הפחות משותף של כל המכנים במשוואה. ה- LCD הוא (ש-4) (ש-3). נקה את השברים על ידי הכפלת שני צידי המשוואה ב- LCD. 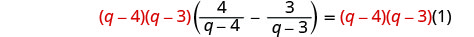
להפיץ. 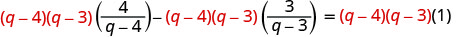
הסר גורמים נפוצים. 
לפשט. 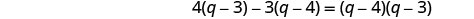
לפשט. 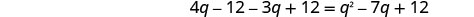
לשלב מונחים כמו. 
לפתור. ראשית כתוב בצורה סטנדרטית. 
פקטור. 
השתמש במאפיין מוצר אפס. 
לא קיבלנו 4 או 3 כפתרונות אלגבריים. 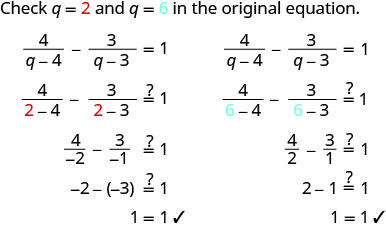
לפתור:\(\frac{2}{x+5}−\frac{1}{x−1}=1\).
- תשובה
-
-1, -2
לפתור:\(\frac{3}{x+8}−\frac{2}{x−2}=1\).
- תשובה
-
-2, -3
לפתור:\(\frac{m+11}{m^2−5m+4}=\frac{5}{m−4}−\frac{3}{m−1}\).
- תשובה
-
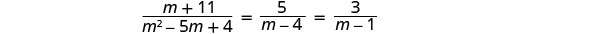
פקטור את כל המכנים, כך שנוכל לציין כל ערך של המשתנה שיהפוך כל מכנה לאפס. 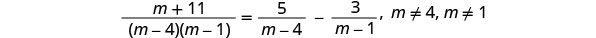
מצא את המכנה הפחות משותף של כל המכנים במשוואה. ה- LCD הוא (m−4) (m−1) נקה את השברים. 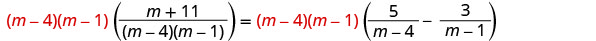
להפיץ. 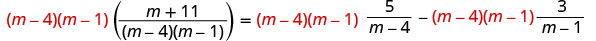
הסר גורמים נפוצים. 
לפשט. 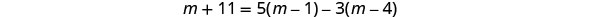
לפתור את המשוואה המתקבלת. 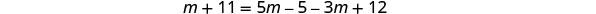

בדוק. הפיתרון האלגברי היחיד היה 4, אך אמרנו ש -4 יהפוך מכנה שווה לאפס. הפתרון האלגברי הוא פתרון חיצוני. אין פתרון למשוואה הזו.
לפתור:\(\frac{x+13}{x^2−7x+10}=\frac{6}{x−5}−\frac{4}{x−2}\).
- תשובה
-
אין פתרון
לפתור:\(\frac{y−14}{y^2+3y−4}=\frac{2}{y+4}+\frac{7}{y−1}\).
- תשובה
-
אין פתרון
למשוואה שפתרנו בדוגמה היה רק פתרון אלגברי אחד, אבל זה היה פתרון זר. זה לא השאיר לנו פתרון למשוואה. למשוואות מסוימות אין פתרון.
לפתור:\(\frac{n}{12}+\frac{n+3}{3n}=\frac{1}{n}\).
- תשובה
-
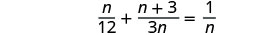
שימו לב לכל ערך של המשתנה שיהפוך כל מכנה לאפס. 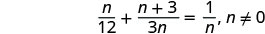
מצא את המכנה הפחות משותף של כל המכנים במשוואה. LCD הוא 12n. נקה את השברים על ידי הכפלת שני צידי המשוואה ב- LCD. 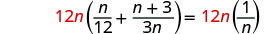
להפיץ. 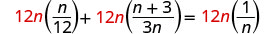
הסר גורמים נפוצים. 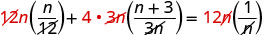
לפשט. 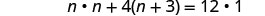
לפתור את המשוואה המתקבלת. 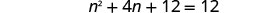
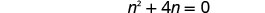
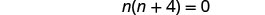
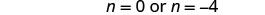
בדוק. n=0 הוא פתרון חיצוני. 
לפתור:\(\frac{x}{18}+\frac{x+6}{9x}=\frac{2}{3x}\).
- תשובה
-
-2
לפתור:\(\frac{y+5}{5y}+\frac{y}{15}=\frac{1}{y}\).
- תשובה
-
-3
לפתור:\(\frac{y}{y+6}=\frac{72}{y^2−36}+4\).
- תשובה
-
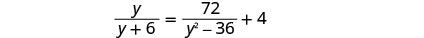
פקטור את כל המכנים, כך שנוכל לציין כל ערך של המשתנה שיהפוך כל מכנה לאפס. 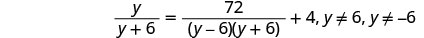
מצא את המכנה הפחות משותף. ה- LCD הוא (y−6) (y+6). נקה את השברים. 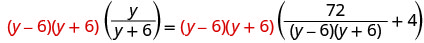
לפשט. 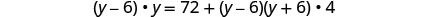
לפשט. 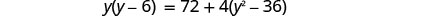
לפתור את המשוואה המתקבלת. 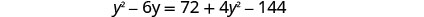
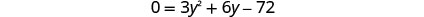
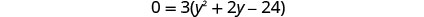
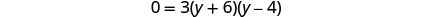
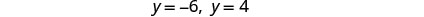
בדוק. y=−6 הוא פתרון זר. 
לפתור:\(\frac{x}{x+4}=\frac{32}{x^2−16}+5\).
- תשובה
-
-4, 3
לפתור:\(\frac{y}{y+8}=\frac{128}{y^2−64}+9\).
- תשובה
-
7
לפתור:\(\frac{x}{2x−2}−\frac{2}{3x+3}=\frac{5x^2−2x+9}{12x^2−12}\).
- תשובה
-
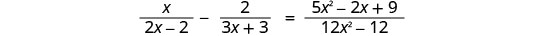
נתחיל בפקטוריזציה של כל המכנים, כדי להקל על זיהוי פתרונות זרים ו- LCD. 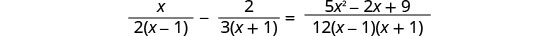
שימו לב לכל ערך של המשתנה שיהפוך כל מכנה לאפס. 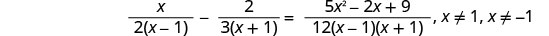
מצא את המכנה הפחות משותף. ה- LCD הוא 12 (x−1) (x+1) נקה את השברים. 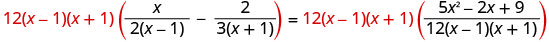
לפשט. 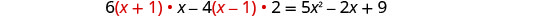
לפשט. 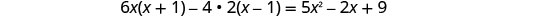
לפתור את המשוואה המתקבלת. 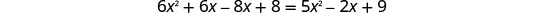
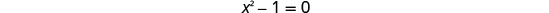
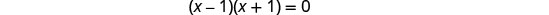
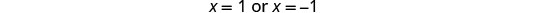
בדוק. איקס=1 ו איקס=−1 הם פתרונות זרים.
למשוואה אין פתרון.
לפתור:\(\frac{y}{5y−10}−\frac{5}{3y+6}=\frac{2y^2−19y+54}{15y^2−60}\).
- תשובה
-
אין פתרון
לפתור:\(\frac{z^2}{z+8}−\frac{3}{4z−8}=\frac{3z^2−16z−68}{z^2+8z−64}\).
- תשובה
-
אין פתרון
לפתור משוואה רציונלית עבור משתנה ספציפי
כאשר פתרנו משוואות לינאריות, למדנו כיצד לפתור נוסחה למשתנה ספציפי. נוסחאות רבות המשמשות בעסקים, מדע, כלכלה ותחומים אחרים משתמשות במשוואות רציונליות כדי לדגמן את הקשר בין שני משתנים או יותר. כעת נראה כיצד לפתור משוואה רציונלית למשתנה ספציפי.
נתחיל בנוסחה המתייחסת למרחק, קצב וזמן. השתמשנו בו פעמים רבות בעבר, אך בדרך כלל לא בצורה זו.
לפתור: \(\frac{D}{T}=R\) עבור T.
- תשובה
-
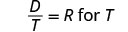
שימו לב לכל ערך של המשתנה שיהפוך כל מכנה לאפס. 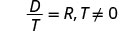
נקה את השברים על ידי הכפלת שני הצדדים של המשוואות על ידי LCD, T. 
לפשט. 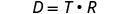
חלק את שני הצדדים ב - R כדי לבודד את T. 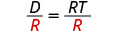
לפשט. 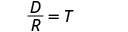
לפתור: \(\frac{A}{L}=W\) עבור L.
- תשובה
-
\(L=\frac{A}{W}\)
לפתור: \(\frac{F}{A}=M\) עבור A.
- תשובה
-
\(A=\frac{F}{M}\)
דוגמה משתמשת בנוסחה לשיפוע שהשתמשנו בה כדי לקבל את צורת שיפוע הנקודה של משוואה של קו.
לפתור: \(m=\frac{x−2}{y−3}\) עבור y.
- תשובה
-
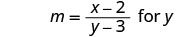
שימו לב לכל ערך של המשתנה שיהפוך כל מכנה לאפס. 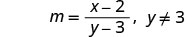
נקה את השברים על ידי הכפלת שני הצדדים של המשוואות על ידי LCD, y−3. 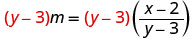
לפשט. 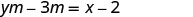
לבודד את המונח עם y. 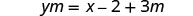
חלקו את שני הצדדים ב - m כדי לבודד את y. 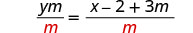
לפשט. 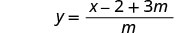
לפתור: \(\frac{y−2}{x+1}=\frac{2}{3}\) עבור x.
- תשובה
-
\(x=\frac{3y−8}{2}\)
לפתור: \(x=\frac{y}{1−y}\) עבור y.
- תשובה
-
\(y=\frac{x}{1+x}\)
הקפד לבצע את כל השלבים בדוגמה. זה אולי נראה כמו נוסחה מאוד פשוטה, אך איננו יכולים לפתור אותה באופן מיידי עבור אף אחד מהמכנים.
לפתור \(\frac{1}{c}+\frac{1}{m}=1\) עבור ג.
- תשובה
-
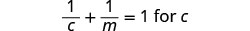
שימו לב לכל ערך של המשתנה שיהפוך כל מכנה לאפס. 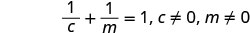
נקה את השברים על ידי הכפלת שני הצדדים של המשוואות על ידי LCD, ס"מ 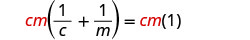
להפיץ. 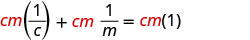
לפשט. 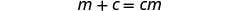
אסוף את התנאים עם c מימין. 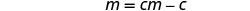
פקטור הביטוי מימין. 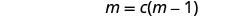
כדי לבודד ג, חלק את שני הצדדים ב- m−1. 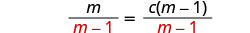
פשט על ידי הסרת גורמים נפוצים. 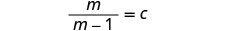
שימו לב שלמרות שלא כללנו את c = 0 ו- m = 0 מהמשוואה המקורית, עלינו לציין זאת כעת. \(m \ne 1\)
לפתור: \(\frac{1}{a}+\frac{1}{b}=c\) עבור א.
- תשובה
-
\(a=\frac{b}{cb−1}\)
לפתור: \(\frac{2}{x}+\frac{1}{3}=\frac{1}{y}\) עבור y.
- תשובה
-
\(y=\frac{3x}{6+x}\)
מושגי מפתח
- אסטרטגיה לפתרון משוואות עם ביטויים רציונליים
- שימו לב לכל ערך של המשתנה שיהפוך כל מכנה לאפס.
- מצא את המכנה הפחות משותף של כל המכנים במשוואה.
- נקה את השברים על ידי הכפלת שני צידי המשוואה ב- LCD.
- לפתור את המשוואה המתקבלת.
- בדוק.
- אם ערכים כלשהם שנמצאים בשלב 1 הם פתרונות אלגבריים, מחק אותם.
- בדוק את כל הפתרונות שנותרו במשוואה המקורית.
רשימת מילים
- משוואה רציונלית
- משוואה רציונלית היא שני ביטויים רציונליים המחוברים בסימן שווה.
- פתרון חיצוני למשוואה רציונלית
- פתרון זר למשוואה רציונלית הוא פתרון אלגברי שיגרום לכל אחד מהביטויים במשוואה המקורית להיות בלתי מוגדר.


