Skip to main content
Global

8.5: פשט ביטויים רציונליים מורכבים

  1. Last updated
  2. Save as PDF
  • Page ID
    205508

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    מטרות למידה

    בסוף פרק זה תוכל:

    • פשט ביטוי רציונלי מורכב על ידי כתיבתו כחלוקה
    • פשט ביטוי רציונלי מורכב באמצעות ה- LCD
    הערה

    לפני שתתחיל, קח את חידון המוכנות הזה.

    אם אתה מפספס בעיה, חזור לסעיף המפורט ובדוק את החומר.

    1. פשט:\(\frac{\frac{3}{5}}{\frac{9}{10}}\).
      אם פספסת בעיה זו, סקור את תרגיל 1.6.25.
    2. פשט:\(\frac{1−\frac{1}{3}}{4^2+4·5}\).
      אם פספסת בעיה זו, סקור את תרגיל 1.6.31.

    שברים מורכבים הם שברים שבהם המונה או המכנה מכילים שבר. בפרק 1 פשטנו שברים מורכבים כמו אלה:

    \[\begin{array}{cc} {\frac{\frac{3}{4}}{\frac{5}{8}}}&{\frac{\frac{x}{2}}{\frac{xy}{6}}}\\ \nonumber \end{array}\]

    בחלק זה נפשט ביטויים רציונליים מורכבים, שהם ביטויים רציונליים עם ביטויים רציונליים במונה או במכנה.

    הגדרה: ביטוי רציונלי מורכב

    ביטוי רציונלי מורכב הוא ביטוי רציונלי בו המונה או המכנה מכילים ביטוי רציונלי.

    הנה כמה ביטויים רציונליים מורכבים:

    \(\frac{\frac{4}{y−3}}{\frac{8}{y^2−9}}\)

    \(\frac{\frac{1}{x}+\frac{1}{y}}{\frac{x}{y}−\frac{y}{x}}\)

    \(\frac{\frac{2}{x+6}}{\frac{4}{x−6}−\frac{4}{x^2−36}}\)
    זכור, אנו תמיד שוללים ערכים שיהפכו כל מכנה לאפס.

    נשתמש בשתי שיטות כדי לפשט ביטויים רציונליים מורכבים.

    פשט ביטוי רציונלי מורכב על ידי כתיבתו כחטיבה

    כבר ראינו את הביטוי הרציונלי המורכב הזה מוקדם יותר בפרק זה.

    \(\frac{\frac{6x^2−7x+2}{4x−8}}{\frac{2x^2−8x+3}{x^2−5x+6}}\)

    ציינו כי פסי שברים אומרים לנו להתחלק, ולכן כתבו אותו מחדש כבעיית החלוקה

    \((\frac{6x^2−7x+2}{4x−8})÷(\frac{2x^2−8x+3}{x^2−5x+6})\)

    ואז הכפלנו את הביטוי הרציונלי הראשון בהדדיות של השני, בדיוק כמו שאנחנו עושים כשאנחנו מחלקים שני שברים.

    זוהי שיטה אחת לפשט ביטויים רציונליים. אנחנו כותבים את זה כאילו אנחנו מחלקים שני שברים.

    דוגמא \(\PageIndex{1}\)

    \(\frac{\frac{4}{y−3}}{\frac{8}{y^2−9}}\).

    תשובה
      \(\frac{\frac{4}{y−3}}{\frac{8}{y^2−9}}\)
    כתוב מחדש את השבר המורכב כחלוקה. \(\frac{4}{y−3}÷\frac{8}{y^2−9}\)
    שכתוב כתוצר של הפעמים הראשונות ההדדיות של השנייה. \(\frac{4}{y−3}·\frac{y^2−9}{8}\)
    להכפיל. \(\frac{4(y^2−9)}{8(y−3)}\)
    גורם לחפש גורמים משותפים. \(\frac{4(y−3)(y+3)}{8(y−3)}\)
    לפשט. \(\frac{y+3}{2}\)

    האם יש ערך (ים) של y שאסור לאפשר? לביטוי הרציונלי הפשוט יש רק קבוע במכנה. אבל לביטוי הרציונלי המורכב המקורי היו מכנים של y-3 ו. \(y^2−9\) ביטוי זה לא יהיה מוגדר אם y = 3 או y = −3

    דוגמא \(\PageIndex{2}\)

    \(\frac{\frac{2}{x^2−1}}{\frac{3}{x+1}}\).

    תשובה

    \(\frac{2}{3(x−1)}\)

    דוגמא \(\PageIndex{3}\)

    \(\frac{\frac{1}{x^2−7x+12}}{\frac{2}{x−4}}\).

    תשובה

    \(\frac{1}{2(x−3)}\)

    דוגמא \(\PageIndex{4}\)

    \(\frac{\frac{1}{3}+\frac{1}{6}}{\frac{1}{2}−\frac{1}{3}}\).

    תשובה
      .
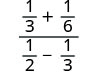
    פשט את המונה והמכנה.  
    מצא את ה- LCD והוסף את השברים במונה.
    מצא את ה- LCD והוסף את השברים במכנה.    		 .
    פשט את המונה והמכנה. .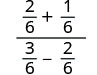
    פשט שוב את המונה והמכנה. .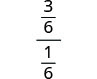
    כתוב מחדש את הביטוי הרציונלי המורכב כבעיית חלוקה. .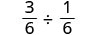
    הכפל את הפעמים הראשונות בהדדיות של השנייה. .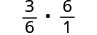
    לפשט. .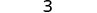
    דוגמא \(\PageIndex{5}\)

    \(\frac{\frac{1}{2}+\frac{2}{3}}{\frac{5}{6}+\frac{1}{12}}\).

    תשובה

    \(\frac{14}{11}\)

    דוגמא \(\PageIndex{6}\)

    \(\frac{\frac{3}{4}−\frac{1}{3}}{\frac{1}{8}+\frac{5}{6}}\).

    תשובה

    \(\frac{10}{23}\)

    כיצד לפשט ביטוי רציונלי מורכב על ידי כתיבתו כחטיבה

    דוגמא \(\PageIndex{7}\)

    \(\frac{\frac{1}{x}+\frac{1}{y}}{\frac{x}{y}−\frac{y}{x}}\).

    תשובה

    התמונה לעיל כוללת שלוש עמודות. התמונה מציגה שלבים כיצד לחלק ביטויים רציונליים מורכבים בשלושה שלבים. שלב ראשון הוא לפשט את המונה והמכנה. אנו נפשט את הסכום במונה ואת ההבדל במכנה לדוגמא 1 חלקי x פלוס 1 חלקי y מחולק ב- x חלקי y מחולק ב- y מינוס y חלקי x מצא מכנה משותף והוסף את השברים במונה ומצא מכנה משותף ונגרע את השברים במונה כדי לקבל 1 פעמים y מחולק על ידי x פעמים y פלוס 1 פעמים x חלקי y חלקי y פי y חלקי y פעמים y חלקי y פעמים y חלקי y פעמים x חלקי y פעמים x חלקי y פעמים y חלקי y פי y חלקי y פעמים y חלקי y פי y חלקי y פעמים y חלקי y פי y חלקי y פעמים y חלקי y פי y חלקי y פעמים y חלקי y פי y חלקי y פעמים y חלקי y פעמים x חלקי y פעמים x חלקי x חלקי x y פעמים x מינוס y כפול y חלקי x פעמים y ואז נקבל y מחולק ב- x y פלוס x פלוס x y חלקי x בריבוע חלקי x y מחולק ב- x y מינוס y בריבוע מחולק על ידי x y. עכשיו יש לנו רק ביטוי רציונלי אחד במונה ואחד במכנה, y פלוס x חלקי x y חלקי x בריבוע מינוס y בריבוע חלקי x y.שלב שני הוא לשכתב את הביטוי הרציונלי המורכב כבעיית חלוקה. אנו כותבים את המונה מחולק במכנה.שלב שלישי הוא לחלק את הביטויים. הכפל את הראשון בהדדיות של השני כדי לקבל y פלוס x מחולק ב- x y פעמים x y חלקי x בריבוע מינוס y בריבוע. פקטור ביטויים כלשהם במידת האפשר. עכשיו יש לנו x y פעמים y פלוס x מחולק x y פעמים x מינוס y פעמים x x פלוס y הסר גורמים נפוצים. חצו את x, y ו- y פלוס x מהמונה. חצו את x, y ו- x פלוס y מהמכנה. פשט כדי לקבל 1 מחולק על ידי x מינוס y.

    דוגמא \(\PageIndex{8}\)

    \(\frac{\frac{1}{x}+\frac{1}{y}}{\frac{1}{x}−\frac{1}{y}}\).

    תשובה

    \(\frac{y+x}{y−x}\)

    דוגמא \(\PageIndex{9}\)

    \(\frac{\frac{1}{a}+\frac{1}{b}}{\frac{1}{a^2}−\frac{1}{b^2}}\).

    תשובה

    \(\frac{ab}{b−a}\)

    הגדרה: פשט ביטוי רציונלי מורכב על ידי כתיבתו כחלוקה.
    1. פשט את המונה והמכנה.
    2. כתוב מחדש את הביטוי הרציונלי המורכב כבעיית חלוקה.
    3. חלק את הביטויים.
    דוגמא \(\PageIndex{10}\)

    \(\frac{n−\frac{4n}{n+5}}{\frac{1}{n+5}+\frac{1}{n−5}}\)

    תשובה
      .
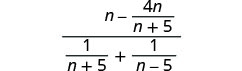
    פשט את המונה והמכנה.  
    מצא את ה- LCD והוסף את השברים במונה.
    מצא את ה- LCD והוסף את השברים במכנה.    		 .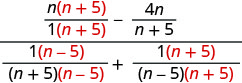
    פשט את המספרים. .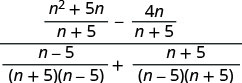

    הפחת את הביטויים הרציונליים במונה והוסף את המכנה.    		 .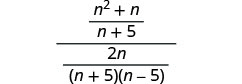
    כתוב מחדש כחלוקת שברים. .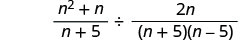
    הכפל את הפעמים הראשונות ההדדיות של השנייה. .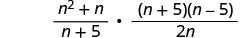
    פקטור ביטויים כלשהם במידת האפשר. .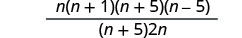
    הסר גורמים נפוצים. .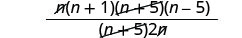
    לפשט. .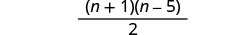
    דוגמא \(\PageIndex{11}\)

    \(\frac{b−\frac{3b}{b+5}}{\frac{2}{b+5}+\frac{1}{b−5}}\).

    תשובה

    ב (ב+2)

    דוגמא \(\PageIndex{12}\)

    \(\frac{1−\frac{3}{c+4}}{\frac{1}{c+4}+\frac{c}{3}}\).

    תשובה

    3c+3

    פשט ביטוי רציונלי מורכב באמצעות ה- LCD

    "פינינו" את השברים על ידי הכפלת ה- LCD כאשר פתרנו משוואות עם שברים. אנו יכולים להשתמש באסטרטגיה זו כאן כדי לפשט ביטויים רציונליים מורכבים. נכפיל את המונה והמכנה על ידי LCD של כל הביטויים הרציונליים.

    בואו נסתכל על הביטוי הרציונלי המורכב שפשטנו בדרך אחת בדוגמה. אנו נפשט את זה כאן על ידי הכפלת המונה והמכנה על ידי ה- LCD. כאשר אנו מכפילים על ידי \(\frac{LCD}{LCD}\) אנו מכפילים ב -1, כך שהערך נשאר זהה.

    דוגמא \(\PageIndex{13}\)

    פשט:\(\frac{\frac{1}{3}+\frac{1}{6}}{\frac{1}{2}−\frac{1}{3}}\).

    תשובה
      .
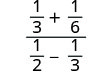
    ה- LCD של כל השברים בביטוי כולו הוא 6.  
    נקה את השברים על ידי הכפלת המונה והמכנה באותו LCD. .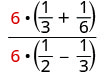
    להפיץ. .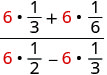
    לפשט. .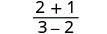
      .
      .
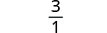
    דוגמא \(\PageIndex{14}\)

    פשט:\(\frac{\frac{1}{2}+\frac{1}{5}}{\frac{1}{10}+\frac{1}{5}}\).

    תשובה

    \(\frac{7}{3}\)

    דוגמא \(\PageIndex{15}\)

    פשט:\(\frac{\frac{1}{4}+\frac{3}{8}}{\frac{1}{2}−\frac{5}{16}}\).

    תשובה

    \(\frac{7}{3}\)

    כיצד לפשט ביטוי רציונלי מורכב באמצעות LCD

    דוגמא \(\PageIndex{16}\)

    פשט:\(\frac{\frac{1}{x}+\frac{1}{y}}{\frac{x}{y}−\frac{y}{x}}\).

    תשובה

    התמונה לעיל כוללת 3 עמודות. הוא מציג את השלבים כיצד לפשט ביטוי רציונלי מורכב באמצעות ה- LCD עבור 1 חלקי x פלוס 1 חלקי y מחולק ב- x מחולק ב- y מינוס y חלקי x חלקי x שלב ראשון הוא למצוא את ה- LCD של כל השברים בביטוי הרציונלי המורכב. ה- LCD של כל השברים הוא x y הכפל את המונה והמכנה על ידי ה- LCD.שלב שני הוא להכפיל גם את המונה וגם את המכנה ב- x y כדי לקבל x y כפול 1 חלקי x פלוס 1 חלקי y מחולק x y כפול x חלקי y חלקי y חלקי x.שלב שלישי הוא לפשט את הביטוי. הפץ כדי לקבל x y כפול 1 חלקי x פלוס x y כפול 1 חלקי y חלקי y חלקי x y כפול x חלקי y חלקי y מינוס x y פעמים y חלקי x. פשט לקבל y פלוס x חלקי x בריבוע מינוס y בריבוע. הסר גורמים נפוצים. חצו את y פלוס x במונה. חצו את x פלוס y במונה. פשט כדי לקבל 1 מחולק על ידי x מינוס y.

    דוגמא \(\PageIndex{17}\)

    פשט:\(\frac{\frac{1}{a}+\frac{1}{b}}{\frac{a}{b}−\frac{b}{a}}\).

    תשובה

    \(\frac{b+a}{a^2+b^2}\)

    דוגמא \(\PageIndex{18}\)

    פשט:\(\frac{\frac{1}{x^2}−\frac{1}{y^2}}{\frac{1}{x}−\frac{1}{y}}\).

    תשובה

    \(\frac{y−x}{xy}\)

    הגדרה: פשט ביטוי רציונלי מורכב באמצעות ה- LCD.
    1. מצא את ה- LCD של כל השברים בביטוי הרציונלי המורכב.
    2. הכפל את המונה והמכנה על ידי ה- LCD.
    3. פשט את הביטוי.

    הקפד להתחיל בפקטוריזציה של כל המכנים כדי שתוכל למצוא את ה- LCD.

    דוגמא \(\PageIndex{19}\)

    פשט:\(\frac{\frac{2}{x+6}}{\frac{4}{x−6}−\frac{4}{x^2−36}}\).

    תשובה
      .
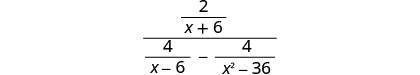
    מצא את ה- LCD של כל השברים בביטוי הרציונלי המורכב. LCD הוא (x+6) (x−6)  
    הכפל את המונה והמכנה על ידי ה- LCD. .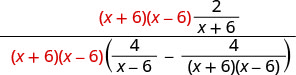
    פשט את הביטוי.  
    להפיץ במכנה. .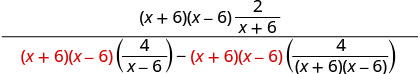
    לפשט. .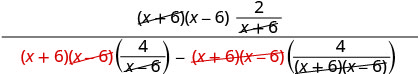
    לפשט. .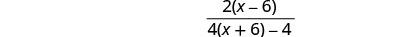
    כדי לפשט את המכנה, להפיץ ולשלב מונחים דומים. .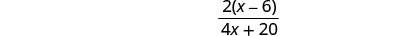
    הסר גורמים נפוצים. .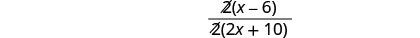
    לפשט. .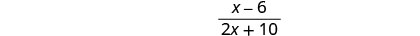
    שימו לב שאין עוד גורמים המשותפים למונה ולמכנה.  
    דוגמא \(\PageIndex{20}\)

    פשט:\(\frac{\frac{3}{x+2}}{\frac{5}{x−2}−\frac{3}{x^2−4}}\).

    תשובה

    \(\frac{3x−6}{5x+7}\)

    דוגמא \(\PageIndex{21}\)

    פשט:\(\frac{\frac{2}{x−7}−\frac{1}{x+7}}{\frac{6}{x+7}−\frac{1}{x^2−49}}\).

    תשובה

    \(\frac{x+21}{6x+43}\)

    דוגמא \(\PageIndex{22}\)

    פשט:\(\frac{\frac{4}{m^2−7m+12}}{\frac{3}{m−3}−\frac{2}{m−4}}\).

    תשובה
      .
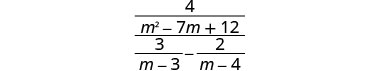
    מצא את ה- LCD של כל השברים בביטוי הרציונלי המורכב. ה- LCD הוא (m−3) (m−4)  
    הכפל את המונה והמכנה על ידי ה- LCD. .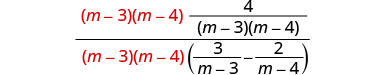
    לפשט. .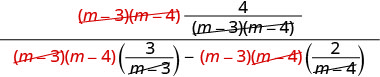
    לפשט. .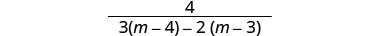
    להפיץ. .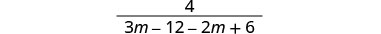
    לשלב מונחים כמו. .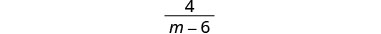
    דוגמא \(\PageIndex{23}\)

    פשט:\(\frac{\frac{3}{x^2+7x+10}}{\frac{4}{x+2}+\frac{1}{x+5}}\).

    תשובה

    \(\frac{3}{5x+22}\)

    דוגמא \(\PageIndex{24}\)

    פשט:\(\frac{\frac{4y}{y+5}+\frac{2}{y+6}}{\frac{3y}{y^2+11y+30}}\).

    תשובה

    \(\frac{6y+34}{3y}\)

    דוגמא \(\PageIndex{25}\)

    פשט:\(\frac{\frac{y}{y+1}}{1+\frac{1}{y−1}}\).

    תשובה
      .
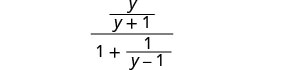
    מצא את ה- LCD של כל השברים בביטוי הרציונלי המורכב.  
    ה- LCD הוא (y+1) (y−1)  
    הכפל את המונה והמכנה על ידי ה- LCD. .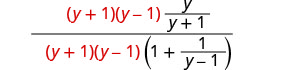
    להפיץ במכנה ולפשט. .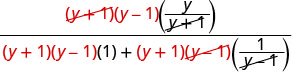
    לפשט. .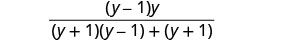
    פשט את המכנה והשאיר את המונה בחשבון. .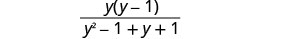
      .
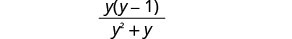
    קח בחשבון את המכנה והסר גורמים המשותפים למונה. .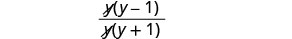
    לפשט. .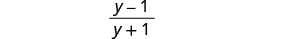
    דוגמא \(\PageIndex{26}\)

    פשט:\(\frac{\frac{x}{x+3}}{1+\frac{1}{x+3}}\).

    תשובה

    \(\frac{x}{x+4}\)

    דוגמא \(\PageIndex{27}\)

    פשט:\(\frac{1+\frac{1}{x−1}}{\frac{3}{x+1}}\).

    תשובה

    \(\frac{x(x+1)}{3(x−1)}\)

    מושגי מפתח

    • לפשט ביטוי רציונלי על ידי כתיבתו כחטיבה
      1. פשט את המונה והמכנה.
      2. כתוב מחדש את הביטוי הרציונלי המורכב כבעיית חלוקה.
      3. חלק את הביטויים.
    • כדי לפשט ביטוי רציונלי מורכב באמצעות LCD
      1. מצא את ה- LCD של כל השברים בביטוי הרציונלי המורכב.
      2. הכפל את המונה והמכנה על ידי ה- LCD.
      3. פשט את הביטוי.

    רשימת מילים

    ביטוי רציונלי מורכב
    ביטוי רציונלי מורכב הוא ביטוי רציונלי בו המונה או המכנה מכילים ביטוי רציונלי.