8.2: הכפל וחלק ביטויים רציונליים
- Page ID
- 205491
בסוף פרק זה, תוכל:
- הכפל ביטויים רציונליים
- חלקו ביטויים רציונליים
לפני שתתחיל, קח את חידון המוכנות הזה.
אם אתה מפספס בעיה, חזור לסעיף המפורט ובדוק את החומר.
- הכפל:\(\frac{14}{15}·\frac{6}{35}\).
אם פספסת בעיה זו, סקור את תרגיל 1.6.13. - לחלק:\(\frac{14}{15}÷\frac{6}{35}\).
אם פספסת בעיה זו, סקור את תרגיל 1.6.22. - גורם לחלוטין:\(2x^2−98\).
אם פספסת בעיה זו, עיין בתרגיל 7.5.10. - גורם לחלוטין:\(10n^3+10\).
אם פספסת בעיה זו, עיין בתרגיל 7.5.19. - גורם לחלוטין:\(10p^2−25pq−15q^2\).
אם פספסת בעיה זו, עיין בתרגיל 7.5.28.
הכפל ביטויים רציונליים
כדי להכפיל ביטויים רציונליים, אנו עושים בדיוק את מה שעשינו עם שברים מספריים. אנו מכפילים את המספרים ומכפילים את המכנים. לאחר מכן, אם ישנם גורמים נפוצים, אנו מסירים אותם כדי לפשט את התוצאה.
אם p, q, r, s הם פולינומים איפה ו \(q \ne 0\) \(s \ne 0\)
\(\frac{p}{q}·\frac{r}{s}=\frac{pr}{qs}\)כדי להכפיל ביטויים רציונליים, הכפל את המספרים והכפיל את המכנים.
נעשה את הדוגמה הראשונה עם שברים מספריים כדי להזכיר לנו כיצד הכפלנו שברים ללא משתנים.
הכפל:\(\frac{10}{28}·\frac{8}{15}\).
- תשובה
-
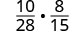
הכפל את המספרים והמכנים. 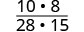
חפש גורמים נפוצים ולאחר מכן הסר אותם. 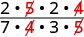
לפשט. 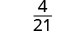
רב-שכבתי:. \(\frac{6}{10}·\frac{15}{12}\)
- תשובה
-
\(\frac{3}{4}\)
רב-שכבתי:. \(\frac{20}{15}·\frac{6}{8}\)
- תשובה
-
1
זכור, לאורך פרק זה, נניח שכל הערכים המספריים שיהפכו את המכנה לאפס אינם נכללים. לא נכתוב את ההגבלות על כל ביטוי רציונלי, אך זכור כי המכנה לעולם לא יכול להיות אפס. אז בדוגמה הבאה, \(x \ne 0\) and \(y \ne 0\).
רב-שכבתי:. \(\frac{2x}{3y^2}·\frac{6xy^3}{x^{2}y}\)
- תשובה
-
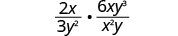
להכפיל. 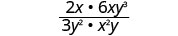
פקטור את המונה והמכנה לחלוטין, ולאחר מכן הסר גורמים משותפים. 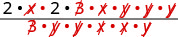
לפשט. 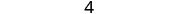
רב-שכבתי:. \(\frac{3pq}{q^2}·\frac{5p^{2}q}{6pq}\)
- תשובה
-
\(\frac{5p^2}{2q}\)
רב-שכבתי:. \(\frac{6x^{3}y}{7x^2}·\frac{2xy}{3x^{2}y}\)
- תשובה
-
\(\frac{12y^3}{7}\)
כיצד להכפיל ביטויים רציונליים
רב-שכבתי:. \(\frac{2x}{x^2-7x+12}·\frac{x^2−9}{6x^2}\)
- תשובה
-
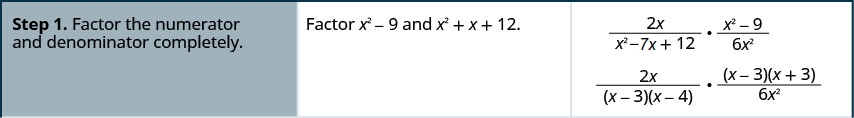


רב-שכבתי:. \(\frac{5x}{x^2+5x+6}·\frac{x^2−4}{10x}\)
- תשובה
-
\(\frac{x−2}{2(x+3)}\)
רב-שכבתי:. \(\frac{9x^2}{x^2+11x+30}·\frac{x^2−36}{3x^2}\)
- תשובה
-
\(\frac{3(x−6)}{x+5}\)
- פקטור כל מונה ומכנה לחלוטין.
- הכפל את המספרים והמכנים.
- פשט על ידי חלוקת גורמים משותפים.
הכפל:\(\frac{n^2−7n}{n^2+2n+1}·\frac{n+1}{2n}\).
- תשובה
-
\(\frac{n^2−7n}{n^2+2n+1}·\frac{n+1}{2n}\) פקטור כל מונה ומכנה. \(\frac{n(n−7)}{(n+1)(n+1)}·\frac{n+1}{2n}\) הכפל את המספרים ואת המכנים. \(\frac{n(n−7)(n+1)}{(n+1)(n+1)2n}\) לפשט. \(\frac{n−7}{2(n+1)}\)
הכפל:\(\frac{x^2−25}{x^2−3x−10}·\frac{x+2}{x}\).
- תשובה
-
\(\frac{x+5}{x}\)
הכפל:\(\frac{x^2−4x}{x^2+5x+6}·\frac{x+2}{x}\).
- תשובה
-
\(\frac{x−4}{x+3}\)
הכפל:\(\frac{16−4x}{2x−12}·\frac{x^2−5x−6}{x^2−16}\).
- תשובה
-
\(\frac{16−4x}{2x−12}·\frac{x^2−5x−6}{x^2−16}\) פקטור כל מונה ומכנה. \(\frac{4(4−x)}{2(x−6)}·\frac{(x−6)(x+1)}{(x−4)(x+4)}\) הכפל את המספרים ואת המכנים. \(\frac{4(4−x)(x−6)(x+1)}{2(x−6)(x−4)(x+4)}\) לפשט. \(−\frac{2(x+1)}{(x+4)}\)
הכפל:\(\frac{12x−6x^2}{x^2+8x}·\frac{x^2+11x+24}{x^2−4}\).
- תשובה
-
\(−\frac{6(x+3)}{x+2}\)
הכפל:\(\frac{9v−3v^2}{9v+36}·\frac{v^2+7v+12}{v^2−9}\).
- תשובה
-
\(−\frac{v}{3}\)
הכפל:\(\frac{2x−6}{x^2−8x+15}·\frac{x^2−25}{2x+10}\).
- תשובה
-
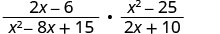
פקטור כל מונה ומכנה. 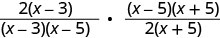
הכפל את המספרים והמכנים. 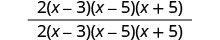
הסר גורמים נפוצים. 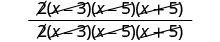
לפשט. 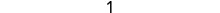
הכפל:\(\frac{3a−21}{a^2−9a+14}·\frac{a^2−4}{3a+6}\).
- תשובה
-
1
הכפל:\(\frac{b^2−b}{b^2+9b−10}·\frac{b^2−100}{b^2−10b}\).
- תשובה
-
1
חלקו ביטויים רציונליים
כדי לחלק ביטויים רציונליים אנו מכפילים את השבר הראשון בהדדיות של השני, בדיוק כמו שעשינו עבור שברים מספריים.
זכור, ההדדי של \(\frac{a}{b}\) הוא\(\frac{b}{a}\). כדי למצוא את ההדדי פשוט שמנו את המונה במכנה ואת המכנה במונה. אנו "הופכים" את השבר.
אם p, q, r, s הם פולינומים שבהם\(q \ne 0\),, \(r \ne 0\) \( s \ne 0\)
\(\frac{p}{q}÷\frac{r}{s}=\frac{p}{q}·\frac{s}{r}\)
כדי לחלק ביטויים רציונליים הכפל את השבר הראשון בהדדיות של השני.
כיצד לחלק ביטויים רציונליים
לחלק:\(\frac{x+9}{6−x}÷\frac{x^2−81}{x−6}\).
- תשובה
-




לחלק:\(\frac{c+3}{5−c}÷\frac{c^2−9}{c−5}\).
- תשובה
-
\(−\frac{1}{c−3}\)
לחלק:\(\frac{2−d}{d−4}÷\frac{4−d^2}{4−d}\).
- תשובה
-
\(−\frac{1}{2+d}\)
- כתוב מחדש את החלוקה כתוצר של הביטוי הרציונלי הראשון וההדדי של השני.
- פקטור את המספרים והמכנים לחלוטין.
- הכפל את המספרים והמכנים יחד.
- פשט על ידי חלוקת גורמים משותפים.
לחלק:\(\frac{3n^2}{n^2−4n}÷\frac{9n^2−45n}{n^2−7n+10}\).
- תשובה
-
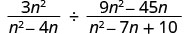
כתוב מחדש את החלוקה כתוצר של הביטוי הרציונלי הראשון וההדדי של השני. 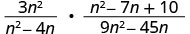
פקחו את המספרים והמכנים ואז הכפלו. 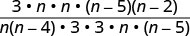
פשט על ידי חלוקת גורמים משותפים. 
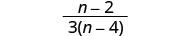
לחלק:\(\frac{2m^2}{m^2−8m}÷\frac{8m^2+24m}{m^2+m−6}\).
- תשובה
-
\(\frac{(m−2)}{4(m−8)}\)
לחלק:\(\frac{15n^2}{3n^2+33n}÷\frac{5n−5}{n^2+9n−22}\).
- תשובה
-
\(\frac{n(n−2)}{n−1}\)
זכור, ראשית כתוב מחדש את החלוקה ככפל של הביטוי הראשון בהדדיות של השני. ואז קחו בחשבון הכל וחפשו גורמים משותפים.
לחלק:\(\frac{2x^2+5x−12}{x^2−16}÷\frac{2x^2−13x+15}{x^2−8x+16}\).
- תשובה
-
\(\frac{2x^2+5x−12}{x^2−16}÷\frac{2x^2−13x+15}{x^2−8x+16}\) כתוב מחדש את החלוקה כתוצר של הביטוי הרציונלי הראשון וההדדי של השני. \(\frac{2x^2+5x−12}{x^2−16}·\frac{x^2−8x+16}{2x^2−13x+15}\) פקחו את המספרים והמכנים ואז הכפלו. \(\frac{(2x−3)(x+4)(x−4)(x−4)}{(x−4)(x+4)(2x−3)(x−5)}\) לפשט. \(\frac{(x−4)}{(x−5)}\)
לחלק:\(\frac{3a^2−8a−3}{a^2−25}÷\frac{3a^2−14a−5}{a^2+10a+25}\).
- תשובה
-
\(\frac{(a−3)(a+5)}{(a−5)(a−5)}\)
לחלק:\(\frac{4b^2+7b−2}{1−b^2}÷\frac{4b^2+15b−4}{b^2−2b+1}\).
- תשובה
-
\(−\frac{(b+2)(b−1)}{(1+b)(b+4)}\)
לחלק:\(\frac{p^3+q^3}{2p^2+2pq+2q^2}÷\frac{p^2−q^2}{6}\).
- תשובה
-
\(\frac{p^3+q^3}{2p^2+2pq+2q^2}÷\frac{p^2−q^2}{6}\) כתוב מחדש את החלוקה כתוצר של הביטוי הרציונלי הראשון וההדדי של השני. \(\frac{p^3+q^3}{2p^2+2pq+2q^2}·\frac{6}{p^2−q^2}\) פקחו את המספרים והמכנים ואז הכפלו. \(\frac{(p+q)(p^2−pq+q^2)6}{2(p^2+pq+q^2)(p−q)(p+q)}\) לפשט. \(\frac{3(p^2−pq+q^2)}{(p−q)(p^2+pq+q^2)}\)
לחלק:\(\frac{x^3−8}{3x^2−6x+12}÷\frac{x^2−4}{6}\).
- תשובה
-
\(\frac{2(x^2+2x+4)}{(x+2)(x^2−2x+4)}\)
לחלק:\(\frac{2z^2}{z^2−1}÷\frac{z^3−z^2+z}{z^3−1}\).
- תשובה
-
\(\frac{2z(z^2+z+1)}{(z+1)(z^2−z+1)}\)
לפני שנעשה את הדוגמה הבאה, בואו נסתכל כיצד אנו מחלקים שבר במספר שלם. כאשר אנו מתחלקים \(\frac{3}{5}÷4\)
\[\begin{array}{c} {\frac{3}{5}÷4}\\ {\frac{3}{5}÷\frac{4}{1}}\\ {\frac{3}{5}·\frac{1}{4}}\\ \nonumber \end{array}\]
אנו עושים את אותו הדבר כאשר אנו מחלקים ביטויים רציונליים.
\(\frac{a^2−b^2}{3ab}÷(a^2+2ab+b^2)\).
- תשובה
-
\(\frac{a^2−b^2}{3ab}÷(a^2+2ab+b^2)\) כתוב את הביטוי השני כשבר. \(\frac{a^2−b^2}{3ab}÷\frac{a^2+2ab+b^2}{1}\) כתוב מחדש את החלוקה כביטוי הראשון כפול ההדדיות של הביטוי השני. \(\frac{a^2−b^2}{3ab}·\frac{1}{a^2+2ab+b^2}\) פקטור את המספרים ואת המכנים, ולאחר מכן להכפיל. \(\frac{(a−b)(a+b)1}{3ab·(a+b)(a+b)}\) לפשט. \(\frac{a−b}{3ab(a+b)}\)
\(\frac{2x^2−14x−16}{4}÷(x2+2x+1)\).
- תשובה
-
\(\frac{x−8}{2(x+1)}\)
\(\frac{y^2−6y+8}{y^2−4y}÷(3y2−12y)\).
- תשובה
-
\(\frac{y−2}{3y(y−4)}\)
\(\frac{\frac{6x^2−7x+2}{4x−8}}{\frac{2x^2−7x+3}{x^2−5x+6}}\).
- תשובה
-
\(\frac{\frac{6x^2−7x+2}{4x−8}}{\frac{2x^2−7x+3}{x^2−5x+6}}\) לשכתב עם סימן חלוקה. \(\frac{6x^2−7x+2}{4x−8}÷\frac{2x^2−7x+3}{x^2−5x+6}\) שכתוב כתוצר של הפעמים הראשונות ההדדיות של השנייה. \(\frac{6x^2−7x+2}{4x−8}·\frac{x^2−5x+6}{2x^2−7x+3}\) פקחו את המספרים והמכנים ואז הכפלו \(\frac{(2x−1)(3x−2)(x−2)(x−3)}{4(x−2)(2x−1)(x−3)}\) לפשט. \(\frac{3x−2}{4}\)
\(\frac{\frac{3x^2+7x+2}{4x+24}}{\frac{3x^2−14x−5}{x^2+x−30}}\).
- תשובה
-
\(\frac{x+2}{4}\)
\(\frac{\frac{y^2−36}{2y^2+11y−6}}{\frac{2y^2−2y−60}{8y−4}}\).
- תשובה
-
\(\frac{2}{y+5}\)
אם יש לנו יותר משני ביטויים רציונליים לעבוד איתם, אנו עדיין פועלים לפי אותו נוהל. השלב הראשון יהיה לשכתב כל חלוקה ככפל על ידי ההדדי. ואז אנו גורמים ומתרבים.
\(\frac{3x−6}{4x−4}·\frac{x^2+2x−3}{x^2−3x−10}÷\frac{2x+12}{8x+16}\).
- תשובה
-
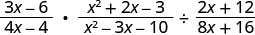
כתוב מחדש את החלוקה ככפל על ידי ההדדי. 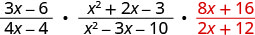
פקטור את המספרים ואת המכנים, ולאחר מכן להכפיל. 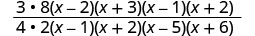
פשט על ידי חלוקת גורמים משותפים. 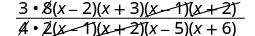
לפשט. 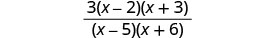
\(\frac{4m+4}{3m−15}·\frac{m^2−3m−10}{m^2−4m−32}÷\frac{12m−36}{6m−48}\).
- תשובה
-
\(\frac{2(m+1)(m+2)}{3(m+4)(m−3)}\)
\(\frac{2n^2+10n}{n−1}÷\frac{n^2+10n+24}{n^2+8n−9}·\frac{n+4}{8n^2+12n}\).
- תשובה
-
\(\frac{(n+5)(n+9)}{2(n+6)(2n+3)}\)
מושגי מפתח
- כפל ביטויים רציונליים
- אם p, q, r, s הם פולינומים איפה \(q \ne 0\) ואז \(s \ne 0\) \(\frac{p}{q}·\frac{r}{s}=\frac{pr}{qs}\)
- כדי להכפיל ביטויים רציונליים, הכפל את המספרים והכפיל את המכנים
- הכפל ביטוי רציונלי
- פקטור כל מונה ומכנה לחלוטין.
- הכפל את המספרים והמכנים.
- פשט על ידי חלוקת גורמים משותפים.
- חלוקת ביטויים רציונליים
- אם p, q, r, s הם פולינומים שבהם\(q \ne 0\),,\(r \ne 0\), \( s \ne 0\) אז \(\frac{p}{q}÷\frac{r}{s}=\frac{p}{q}·\frac{s}{r}\)
- כדי לחלק ביטויים רציונליים הכפל את השבר הראשון בהדדיות של השני.
- חלקו ביטויים רציונליים
- כתוב מחדש את החלוקה כתוצר של הביטוי הרציונלי הראשון וההדדי של השני.
- פקטור את המספרים והמכנים לחלוטין.
- הכפל את המספרים והמכנים יחד.
- פשט על ידי חלוקת גורמים משותפים.


