8.1: פשט ביטויים רציונליים
- Page ID
- 205496
בסוף פרק זה, תוכל:
- קבע את הערכים שעבורם ביטוי רציונלי אינו מוגדר
- להעריך ביטויים רציונליים
- פשט ביטויים רציונליים
- פשט ביטויים רציונליים עם גורמים הפוכים
בפרק 1 סקרנו את תכונות השברים ופעולותיהם. הצגנו מספרים רציונליים, שהם רק שברים שבהם המספרים והמכנים הם מספרים שלמים, והמכנה אינו אפס.
בפרק זה נעבוד עם שברים שהמספרים והמכנים שלהם הם פולינומים. אנחנו קוראים לזה ביטויים רציונליים.
ביטוי רציונלי הוא ביטוי לצורה\(\frac{p(x)}{q(x)}\), כאשר p ו- q הם פולינומים ו. \(q \ne 0\)
הנה כמה דוגמאות לביטויים רציונליים:
\[\begin{array}{cccc} {−\frac{13}{42}}&{\frac{7y}{8z}}&{\frac{5x+2}{x^2−7}}&{\frac{4x^2+3x−1}{2x−8}}\\ \nonumber \end{array}\]
שימו לב שהביטוי הרציונלי הראשון המפורט לעיל\(−\frac{13}{42}\),, הוא רק שבריר. מכיוון שקבוע הוא פולינום עם תואר אפס, היחס בין שני קבועים הוא ביטוי רציונלי, בתנאי שהמכנה אינו אפס.
נבצע אותן פעולות עם ביטויים רציונליים שאנו מבצעים עם שברים. אנו נפשט, נוסיף, נחסר, נכפיל, נחלק ונשתמש בהם ביישומים.
קבע את הערכים שעבורם ביטוי רציונלי אינו מוגדר
כאשר אנו עובדים עם שבר מספרי, קל להימנע מחלוקת באפס, מכיוון שאנו יכולים לראות את המספר במכנה. על מנת להימנע מחלוקת באפס בביטוי רציונלי, אסור לנו לאפשר ערכים של המשתנה שיהפכו את המכנה לאפס.
אם המכנה הוא אפס, הביטוי הרציונלי אינו מוגדר. המונה של ביטוי רציונלי עשוי להיות 0 - אך לא המכנה.
אז לפני שנתחיל פעולה כלשהי עם ביטוי רציונלי, נבחן אותה תחילה כדי למצוא את הערכים שיהפכו את המכנה לאפס. כך, כאשר נפתור משוואה רציונלית למשל, נדע האם הפתרונות האלגבריים שאנו מוצאים מותרים או לא.
- הגדר את המכנה שווה לאפס.
- פתור את המשוואה בקבוצת הריאלים, במידת האפשר.
קבע את הערכים שעבורם הביטוי הרציונלי אינו מוגדר:
- \(\frac{9y}{x}\)
- \(\frac{4b−3}{2b+5}\)
- \(\frac{x+4}{x^2+5x+6x}\)
פתרון
הביטוי לא יוגדר כאשר המכנה הוא אפס.
| 1. | \(\frac{9y}{x}\) |
| הגדר את המכנה שווה לאפס. לפתור עבור המשתנה. | איקס=0 |
| \(\frac{9y}{x}\)אינו מוגדר עבור x = 0. | |
| 2. |
\(\frac{4b−3}{2b+5}\) |
| הגדר את המכנה שווה לאפס. לפתור עבור המשתנה. | 2 ב+5 = 0 |
| 2ב=−5 | |
| \(b=−\frac{5}{2}\) | |
| \(\frac{4b−3}{2b+5}\)אינו מוגדר עבור\(b=−\frac{5}{2}\). | |
| 3. | \(\frac{x+4}{x^2+5x+6x}\) |
| הגדר את המכנה שווה לאפס. לפתור עבור המשתנה. | \(x^2+5x+6x=0\) |
| \((x+2)(x+3)=0\) | |
| איקס+2 = 0 או איקס+3 = 0 | |
| איקס=−2 או איקס=−3 | |
| \(\frac{x+4}{x^2+5x+6x}\)אינו מוגדר עבור איקס=−2 או איקס=−3. |
האמירה שהביטוי הרציונלי \(\frac{x+4}{x^2+5x+6x}\) אינו מוגדר עבור איקס=−2אוקס=−3 דומה לכתיבת הביטוי "בטל היכן שאסור" בכללי התחרות.
נסה את זה \(\PageIndex{2}\)
קבע את הערכים שעבורם הביטוי הרציונלי אינו מוגדר:
- \(\frac{3y}{x}\)
- \(\frac{8n−5}{3n+1}\)
- \(\frac{a+10}{a^2+4a+3a}\)
- Answer
-
- x=0
- \(n=−\frac{1}{3}\)
- a=−1, a=−3
Try It \(\PageIndex{3}\)
קבע את הערכים שעבורם הביטוי הרציונלי אינו מוגדר:
- \(\frac{4p}{5q}\)
- \(\frac{y−1}{3y+2}\)
- \(\frac{m−5}{m^2+m−6}\)
- תשובה
-
- q=0
- \(y=−\frac{2}{3}\)
- מ = 2, מ = −3
הערכת ביטויים רציונליים
כדי להעריך ביטוי רציונלי, אנו מחליפים ערכים של המשתנים בביטוי ומפשטים, בדיוק כפי שיש לנו לביטויים רבים אחרים בספר זה.
הערך \(\frac{2x+3}{3x−5}\) עבור כל ערך:
- איקס=0
- איקס=2
- איקס=−3
פתרון
| 1. |  |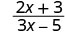
 |
 |
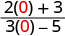| לפשט. |  |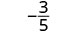
| 2. |  |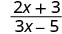
 |
 |
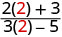| לפשט. |  |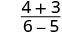
 |
|
 |
|
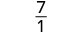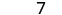| 3. |  |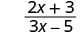
 |
 |
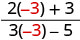| לפשט. |  |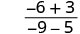
 |
|
 |
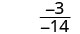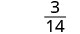נסה את זה \(\PageIndex{5}\)
להעריך \(\frac{y+1}{2y−3}\) for each value:
- y=1
- y=−3
- y=0
- Answer
-
- −2
- \(\frac{2}{9}\)
- \(−\frac{1}{3}\)
Try It \(\PageIndex{6}\)
הערך \(\frac{5x−1}{2x+1}\) עבור כל ערך:
- איקס=1
- איקס=−1
- איקס=0
- תשובה
-
- \(\frac{4}{3}\)
- 6
- -1
הערך \(\frac{x^2+8x+7}{x^2−4}\) עבור כל ערך:
- איקס=0
- איקס=2
- איקס=−1
פתרון
| 1. |  |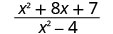
 |
 |
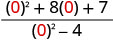| לפשט. |  |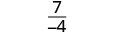
 |
|
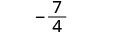| 2. | |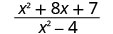
 |
 |
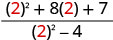| לפשט. |  |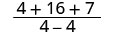
 |
|
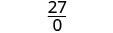| ביטוי רציונלי זה אינו מוגדר עבור x = 2. | |
| 3. |  |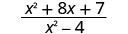
 |
 |
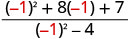| לפשט. |  |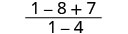
 |
|
 |
|
 |
|
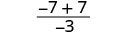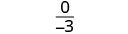נסה את זה \(\PageIndex{8}\)
להעריך \(\frac{x^2+1}{x^2−3x+2}\) for each value:
- x=0
- x=−1
- x=3
- Answer
-
- \(\frac{1}{2}\)
- \(\frac{1}{3}\)
- 2
Try It \(\PageIndex{9}\)
הערך \(\frac{x^2+x−6}{x^2−9}\) עבור כל ערך.
- איקס=0
- איקס=−2
- איקס=1
- תשובה
-
- \(\frac{2}{3}\)
- \(\frac{4}{5}\)
- \(\frac{1}{2}\)
זכור כי שבר מפושט כאשר אין לו גורמים משותפים, מלבד 1, במונה ובמכנה שלו. כאשר אנו מעריכים ביטוי רציונלי, אנו דואגים לפשט את השבר המתקבל.
הערך \(\frac{a^2+2ab+b^2}{3ab}\) עבור כל ערך.
- א=1, ב=2
- א=−2, ב=−1
- \(a=\frac{1}{3}\), b = 0
פתרון
| 1. | \(\frac{a^2+2ab+b^2}{3ab}\)כאשר a=1, b = 2 |
 |
 |
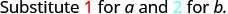| לפשט. |  |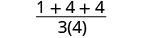
 |
|
 |
|
| 2. | \(\frac{a^2+2ab+b^2}{3ab}\)מתי א=−2, ב=−1 |
 |
 |
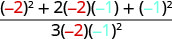| לפשט. |  |
 |
|
 |
|
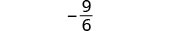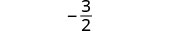| 3. | \(\frac{a^2+2ab+b^2}{3ab}\)מתי\(a=\frac{1}{3}\), b = 0 |
 |
 |
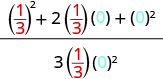| לפשט. |  |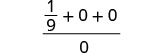
 |
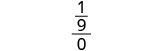נסה את זה \(\PageIndex{11}\)
להעריך \(\frac{2a^{3}b}{a^2+2ab+b^2}\) for each value.
- a=−1, b=2
- a=0, b=−1
- a=1, \(b=\frac{1}{2}\)
- Answer
-
- −4
- 0
- \(\frac{4}{9}\)
Try It \(\PageIndex{12}\)
הערך \(\frac{a^2−b^2}{8ab^3}\) עבור כל ערך:
- א=1, ב=−1
- \(a=\frac{1}{2}\), ב=−1
- א=−2, ב=1
- תשובה
-
- 0
- \(\frac{3}{16}\)
- \(\frac{3}{16}\)
פשט ביטויים רציונליים
בדיוק כמו שבר נחשב לפשוט אם אין גורמים משותפים, מלבד 1, במונה ובמכנה שלו, ביטוי רציונלי מפושט אם אין לו גורמים משותפים, מלבד 1, במונה ובמכנה שלו.
ביטוי רציונלי נחשב לפשוט אם אין גורמים משותפים במונה ובמכנה שלו.
לדוגמה:
- \(\frac{2}{3}\)הוא פשוט כי אין גורמים נפוצים של 2 ו 3.
- \(\frac{2x}{3x}\)אינו מפושט מכיוון ש - x הוא גורם נפוץ של 2 x ו- 3 x.
אנו משתמשים במאפיין השברים המקבילים כדי לפשט שברים מספריים. אנו משחזרים אותו כאן מכיוון שנשתמש בו גם כדי לפשט ביטוי רציונלי s.
אם a, b ו - c הם מספרים שבהם\(b \ne 0\),\(c\ne 0\), ואז \(\frac{a}{b}=\frac{a·c}{b·c}\) ו- \(\frac{a·c}{b·c}=\frac{a}{b}\)
שימו לב שבמאפיין השברים המקבילים, הערכים שיהפכו את המכנים לאפס אסורים באופן ספציפי. אנו רואים\(b \ne 0\), נאמר \(c\ne 0\) בבירור. בכל פעם שאנו כותבים ביטוי רציונלי, עלינו להצהיר הצהרה דומה שאינה מאפשרת ערכים שיהפכו את המכנה לאפס. עם זאת, כדי לאפשר לנו להתמקד בעבודה העומדת על הפרק, נשמיט את כתיבתה בדוגמאות.
נתחיל בבחינת האופן בו אנו מפשטים שברים מספריים.
פשט:\(−\frac{36}{63}\).
פתרון
 |
|
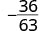| כתוב מחדש את המונה והמכנה המציג את הגורמים המשותפים. |  |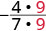
| פשט באמצעות המאפיין שברים שווים. |  |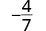
שימו לב שהשבר \(−\frac{4}{7}\) מפושט מכיוון שאין גורמים נפוצים יותר.
נסה את זה \(\PageIndex{14}\)
פשט: \(−\frac{45}{81}\).
- Answer
-
\(−\frac{5}{9}\)
Try It \(\PageIndex{15}\)
פשט:\(−\frac{42}{54}\).
- תשובה
-
\(−\frac{7}{9}\)
לאורך פרק זה נניח כי כל הערכים המספריים שיהפכו את המכנה לאפס אינם נכללים. לא נכתוב את ההגבלות על כל ביטוי רציונלי, אך זכור כי המכנה לעולם לא יכול להיות אפס. אז בדוגמה הבאה, \(x \ne 0\) ו\(y \ne 0\).
פשט:\(\frac{3xy}{18x^{2}y^{2}}\).
פתרון
 |
|
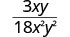| כתוב מחדש את המונה והמכנה המציג את הגורמים המשותפים. |  |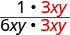
| פשט באמצעות המאפיין שברים שווים. |  |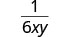
שמתם לב שאלו אותם צעדים שנקטנו כשחילקנו מונומיאלים בפולינומים?
נסה את זה \(\PageIndex{17}\)
פשט: \(\frac{4x^{2}y}{12xy^2}\).
- Answer
-
\(\frac{x}{3y}\)
Try It \(PageIndex{18}\)
פשט:\(\frac{16x^{2}y}{2xy^2}\).
- תשובה
-
\(\frac{8x}{y}\)
היזהר מאוד כשאתה מסיר גורמים נפוצים. גורמים מוכפלים לייצור מוצר. אתה יכול להסיר גורם ממוצר. אינך יכול להסיר מונח מסכום.
שים לב שהסרת ה - x מ- \(\frac{x+5}{x}\) תהיה כמו ביטול ה- 2 בשבריר\(\frac{2+5}{2}\)!
כיצד לפשט בינומים רציונליים
פשט:\(\frac{2x+8}{5x+20}\).
פתרון
נסה את זה \(\PageIndex{20}\)
פשט: \(\frac{3x−6}{2x−4}\).
- Answer
-
\(\frac{3}{2}\)
Try It \(\PageIndex{21}\)
פשט:\(\frac{7y+35}{5y+25}\).
- תשובה
-
\(\frac{7}{5}\)
כעת אנו מסכמים את הצעדים שעליכם לבצע כדי לפשט ביטויים רציונליים.
- פקטור את המונה והמכנה לחלוטין.
- פשט על ידי חלוקת גורמים משותפים.
נשתמש בשיטות שכיסינו בפקטורינג כדי לחשב את הפולינומים במונים ובמכנים בדוגמאות הבאות.
פשט:\(\frac{x^2+5x+6}{x^2+8x+12}\).
פתרון
| \(\frac{x^2+5x+6}{x^2+8x+12}\) | |
| פקטור המונה והמכנה. | \(\frac{(x+2)(x+3)}{(x+2)(x+6)}\) |
| הסר את הגורם המשותף x+2 מהמונה והמכנה. | \(\frac{x+3}{x+6}\) |
האם אתה יכול לדעת אילו ערכים של x חייבים להיכלל בדוגמה זו?
נסה את זה \(\PageIndex{23}\)
פשט: \(\frac{x^2−x−2}{x^2−3x+2}\).
- Answer
-
\(\frac{x+1}{x−1}\)
Try It \(\PageIndex{24}\)
פשט:\(\frac{x^2−3x−10}{x^2+x−2}\).
- תשובה
-
\(\frac{x−5}{x−1}\)
פשט:\(\frac{y^2+y−42}{y^2−36}\).
פתרון
| \(\frac{y^2+y−42}{y^2−36}\). | |
| פקטור המונה והמכנה. | \(\frac{(y+7)(y−6)}{(y+6)(y−6)}\) |
| הסר את הגורם המשותף y−6 מהמונה ומהמכנה. | \(\frac{y+7}{y+6}\) |
נסה את זה \(\PageIndex{26}\)
פשט: \(\frac{x^2+x−6}{x^2−4}\).
- Answer
-
\(\frac{x+3}{x+2}\)
Try It \(\PageIndex{27}\)
פשט:\(\frac{x^2+8x+7}{x^2−49}\).
- תשובה
-
\(\frac{x+1}{x−7}\)
פשט:\(\frac{p^3−2p^2+2p−4}{p^2−7p+10}\).
פתרון
| \(\frac{p^3−2p^2+2p−4}{p^2−7p+10}\) | |
| פקטור את המונה והמכנה, תוך שימוש בקיבוץ כדי לחשב את המונה. | \(\frac{p^2(p−2)+2(p−2)}{(p−5)(p−2)}\) |
| \(\frac{(p^2+2)(p−2)}{(p−5)(p−2)}\) | |
| הסר את הגורם המשותף p−2 מהמונה ומהמכנה. | \(\frac{p^2+2}{p−5}\) |
נסה את זה \(\PageIndex{29}\)
פשט: \(\frac{y^3−3y^2+y−3}{y^2−y−6}\).
- Answer
-
\(\frac{y^2+1}{y+2}\)
Try It \(\PageIndex{30}\)
פשט:\(\frac{p^3−p^2+2p−2}{p^2+4p−5}\).
- תשובה
-
\(\frac{p^2+2}{p+5}\)
פשט:\(\frac{2n^2−14n}{4n^2−16n−48}\).
פתרון
| \(\frac{2n^2−14n}{4n^2−16n−48}\) | |
| פקטור את המונה והמכנה, תחילה פקטר את ה- GCF. | \(\frac{2n(n−7)}{4(n^2−4n−12)}\) |
| \(\frac{2n(n−7)}{4(n−6)(n+2)}\) | |
| הסר את הגורם המשותף, 2. | \(\frac{n(n−7)}{2(n−6)(n+2)}\) |
נסה את זה \(\PageIndex{32}\)
פשט: \(\frac{2n^2−10n}{4n^2−16n−20}\).
- Answer
-
\(\frac{n}{2(n+1)}\)
Try It \(\PageIndex{33}\)
פשט:\(\frac{4x^2−16x}{8x^2−16x−64}\).
- תשובה
-
\(\frac{x}{2(x+2)}\)
פשט:\(\frac{3b^2−12b+12}{6b^2−24}\).
פתרון
| \(\frac{3b^2−12b+12}{6b^2−24}\) | |
| פקטור את המונה והמכנה, תחילה פקטר את ה- GCF. | \(\frac{3(b^2−4b+4)}{6(b^2−4)}\) |
| \(\frac{3(b−2)(b−2)}{6(b−2)(b+2)}\) | |
| הסר את הגורמים הנפוצים של b−2 ו- 3. | \(\frac{3(b−2)}{2(b+2)}\) |
נסה את זה \(\PageIndex{35}\)
פשט: \(\frac{2x^2−12x+18}{3x^2−27}\).
- Answer
-
\(\frac{2(x−3)}{3(x+3)}\)
Try It \(PageIndex{36}\)
פשט:\(\frac{5y^2−30y+25}{2y^2−50}\).
- תשובה
-
\(\frac{5(x−1)}{2(x+5)}\)
פשט:\(\frac{m^3+8}{m^2−4}\).
פתרון
| \(\frac{m^3+8}{m^2−4}\) | |
| פקטור המונה והמכנה, תוך שימוש בנוסחאות לסכום הקוביות והבדל הריבועים. | \(\frac{(m+2)(m^2−2m+4)}{(m+2)(m−2)}\) |
| הסר את הגורמים הנפוצים של m+2. | \(\frac{m^2−2m+4}{m−2}\) |
נסה את זה \(\PageIndex{38}\)
פשט: \(\frac{p^3−64}{p^2−16}\).
- Answer
-
\(\frac{p^2+4p+16}{p+4}\)
Try It \(\PageIndex{39}\)
פשט:\(\frac{x^3+8}{x^2−4}\).
- תשובה
-
\(\frac{x^2−2x+4}{x−2}\)
פשט ביטויים רציונליים עם גורמים מנוגדים
כעת נראה כיצד לפשט ביטוי רציונלי שלמונה ולמכנה יש גורמים הפוכים. נתחיל בשבר מספרי, נניח\(\frac{7}{−7}\).
אנו יודעים שחלק זה מפשט ל -1. אנו גם מכירים בכך שהמונה והמכנה הם ניגודים.
ביסודות הצגנו סימון הפוך: ההפך מ- a הוא −a גם אנחנו זוכרים את זה -a = −1·a
אנו מפשטים את השבר \(\frac{a}{−a}\)
\[\begin{array}{ll} {}&{\frac{a}{−a}}\\ {\text{We could rewrite this.}}&{\frac{1·a}{−1·a}}\\ {\text{Remove the common factors.}}&{\frac{1}{−1}}\\ {\text{Simplify.}}&{−1}\\ \nonumber \end{array}\]
אז, באותו אופן, אנחנו יכולים לפשט את השבר \(\frac{x−3}{−(x−3)}\)
\[\begin{array}{ll} {}&{\frac{x−3}{−(x−3)}}\\ {\text{We could rewrite this.}}&{\frac{1·(x−3)}{−1·(x−3)}}\\ {\text{Remove the common factors.}}&{\frac{1}{−1}}\\ {\text{Simplify.}}&{−1}\\ \nonumber \end{array}\]
אבל ההפך מ- x−3 יכול להיכתב אחרת:
\[\begin{array}{ll} {}&{−(x−3)}\\ {\text{Distribute.}}&{−x+3}\\ {\text{Rewrite.}}&{3−x}\\ \nonumber \end{array}\]
המשמעות היא שהשבר \(\frac{x−3}{3−x}\) מפשט ל -1.
באופן כללי, נוכל לכתוב את ההפך מ- a−b כ- b−a כך שהביטוי \(\frac{a−b}{b−a}\) הרציונלי מפשט ל -1.
ההפך מ- a−b הוא b−a
\(\frac{a−b}{b−a}=−1\), \(a \ne b\)
ביטוי והחלוקה ההפוכה שלו ל -1
נשתמש במאפיין זה כדי לפשט ביטויים רציונליים המכילים ניגודים במונים ובמכנים שלהם.
פשט:\(\frac{x−8}{8−x}\).
פתרון
| \(\frac{x−8}{8−x}\). | |
| הכירו בכך איקס-8 ו-8−איקס הם ניגודים | -1 |
נסה את זה \(\PageIndex{41}\)
פשט: \(\frac{y−2}{2−y}\).
- Answer
-
−1
Try It \(\PageIndex{42}\)
פשט:\(\frac{n−9}{9−n}\).
- תשובה
-
-1
זכרו, הצעד הראשון בפישוט ביטוי רציונלי הוא להביא בחשבון את המונה והמכנה לחלוטין.
פשט:\(\frac{14−2x}{x^2−49}\).
פתרון
 |
|
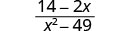| פקטור המונה והמכנה. |  |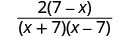
| הכירו 7−x ו- x−7 הם הפכים. |  |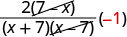
| לפשט. |  |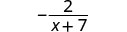
נסה את זה \(\PageIndex{44}\)
פשט: \(\frac{10−2y}{y^2−25}\).
- Answer
-
\(−\frac{2}{y+5}\)
Try It \(\PageIndex{45}\)
פשט:\(\frac{3y−27}{81−y^2}\).
- תשובה
-
\(−\frac{3}{9+y}\)
פשט:\(\frac{x^2−4x−32}{64−x^2}\).
פתרון
 |
|
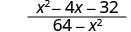| פקטור המונה והמכנה. |  |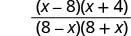
| הכירו את הגורמים שהם ניגודים. |  |
| לפשט. |  |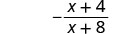
נסה את זה \(\PageIndex{47}\)
פשט: \(\frac{x^2−4x−5}{25−x^2}\).
- Answer
-
\(−\frac{x+1}{x+5}\)
Try It \(\PageIndex{48}\)
פשט:\(\frac{x^2+x−2}{1−x^2}\).
- תשובה
-
\(−\frac{x+2}{x+1}\)
מושגי מפתח
- קבע את הערכים שעבורם ביטוי רציונלי אינו מוגדר
- הגדר את המכנה שווה לאפס.
- לפתור את המשוואה, אם אפשר.
- ביטוי רציונלי פשוט
- ביטוי רציונלי נחשב לפשוט אם אין גורמים משותפים במונה ובמכנה שלו.
- פשט ביטוי רציונלי
- פקטור את המונה והמכנה לחלוטין.
- פשט על ידי חלוקת גורמים משותפים.
- ניגודים בביטוי רציונלי
- ההפך מ- a−b הוא
\(\frac{a−b}{b−a}=−1\) \(a \ne b\) b−a,, \(b \ne 0\) \(a \ne b\)
- ההפך מ- a−b הוא
תרגול הופך מושלם
בתרגילים הבאים, קבע את הערכים שעבורם הביטוי הרציונלי אינו מוגדר.
- \(\frac{2x}{z}\)
- \(\frac{4p−1}{6p−5}\)
- \(\frac{n−3}{n^2+2n−8}\)
- תשובה
-
- z = 0
- \(p=\frac{5}{6}\)
- נ=−4, נ=2
- \(\frac{10m}{11n}\)
- \(\frac{6y+13}{4y−9}\)
- \(\frac{b−8}{b^2−36}\)
- \(\frac{4x^{2}y}{3y}\)
- \(\frac{3x−2}{2x+1}\)
- \(\frac{u−1}{u^2−3u−28}\)
- תשובה
-
- y=0
- \(x=−\frac{1}{2}\)
- u=−4, u=7
- \(\frac{5pq^{2}}{9q}\)
- \(\frac{7a−4}{3a+5}\)
- \(\frac{1}{x^2−4}\)
בתרגילים הבאים, הערך את הביטוי הרציונלי לערכים הנתונים.
\(\frac{2x}{x−1}\)
- איקס=0
- איקס=2
- איקס=−1
- תשובה
-
- 0
- 4
- 1
\(\frac{4y−1}{5y−3}\)
- y=0
- y=2
- y=−1
\(\frac{2p+3}{p^2+1}\)
- p=0
- p=1
- p=−2
- תשובה
-
- 3
- \(\frac{5}{2}\)
- \(−\frac{1}{5}\)
\(\frac{x+3}{2−3x}\)
- איקס=0
- איקס=1
- איקס=−2
\(\frac{y^2+5y+6}{y^2−1}\)
- y=0
- y=2
- y=−2
- תשובה
-
- −6
- \(\frac{20}{3}\)
- 0
\(\frac{z^2+3z−10}{z^2−1}\)
- z = 0
- z=2
- ז=−2
\(\frac{a^2−4}{a^2+5a+4}\)
- a=0
- a=1
- א=−2
- תשובה
-
- -1
- \(−\frac{3}{10}\)
- 0
\(\frac{b^2+2}{b^2−3b−4}\)
- b=0
- b=2
- ב=−2
\(\frac{x^2+3xy+2y^2}{2x^{3}y}\)
- איקס=1, y =−1
- איקס=2, y=1
- איקס=−1, י=−2
- תשובה
-
- 0
- \(\frac{3}{4}\)
- \(\frac{15}{4}\)
\(\frac{c^2+cd−2d^2}{cd^{3}}\)
- ג = 2, ד=−1
- ג=1, ד=−1
- ג = -1, ד=2
\(\frac{m^2−4n^2}{5mn^3}\)
- מ = 2, נ=1
- m=−1, נ=−1
- מ = 3, נ=2
- תשובה
-
- 0
- \(−\frac{3}{5}\)
- \(−\frac{7}{20}\)
\(\frac{2s^{2}t}{s^2−9t^2}\)
- s=4, t = 1
- ס=−1, ט=−1
- s=0, t = 2
בתרגילים הבאים, לפשט.
\(−\frac{4}{52}\)
- תשובה
-
\(−\frac{1}{13}\)
\(−\frac{44}{55}\)
\(\frac{56}{63}\)
- תשובה
-
\(\frac{8}{9}\)
\(\frac{65}{104}\)
\(\frac{6ab^{2}}{12a^{2}b}\)
- תשובה
-
\(\frac{b}{2ab}\)
\(\frac{15xy^{3}}{x^{3}y^{3}}\)
\(\frac{8m^{3}n}{12mn^2}\)
- תשובה
-
\(\frac{2m^2}{3n}\)
\(\frac{36v^{3}w^2}{27vw^3}\)
\(\frac{3a+6}{4a+8}\)
- תשובה
-
\(\frac{3}{4}\)
\(\frac{5b+5}{6b+6}\)
\(\frac{3c−9}{5c−15}\)
- תשובה
-
\(\frac{3}{5}\)
\(\frac{4d+8}{9d+18}\)
\(\frac{7m+63}{5m+45}\)
- תשובה
-
\(\frac{7}{5}\)
\(\frac{8n−96}{3n−36}\)
\(\frac{12p−240}{5p−100}\)
- תשובה
-
\(\frac{12}{5}\)
\(\frac{6q+210}{5q+175}\)
\(\frac{a^2−a−12}{a^2−8a+16}\)
- תשובה
-
\(\frac{a+3}{a−4}\)
\(\frac{x^2+4x−5}{x^2−2x+1}\)
\(\frac{y^2+3y−4}{y^2−6y+5}\)
- תשובה
-
\(\frac{y+4}{y−5}\)
\(\frac{v^2+8v+15}{v^2−v−12}\)
\(\frac{x^2−25}{x^2+2x−15}\)
- תשובה
-
\(\frac{x−5}{x−3}\)
\(\frac{a^2−4}{a^2+6a−16}\)
\(\frac{y^2−2y−3}{y^2−9}\)
- תשובה
-
\(\frac{y+1}{y+3}\)
\(\frac{b^2+9b+18}{b^2−36}\)
\(\frac{y^3+y^2+y+1}{y^2+2y+1}\)
- תשובה
-
\(\frac{y^2+1}{y+1}\)
\(\frac{p^3+3p^2+4p+12}{p^2+p−6}\)
\(\frac{x^3−2x^2−25x+50}{x^2−25}\)
- תשובה
-
איקס-2
\(\frac{q^3+3q^2−4q−12}{q^2−4}\)
\(\frac{3a^2+15a}{6a^2+6a−36}\)
- תשובה
-
\(\frac{a(a+5)}{2(a+3)(a−2)}\)
\(\frac{8b^2−32b}{2b^2−6b−80}\)
\(\frac{−5c^2−10c}{−10c^2+30c+100}\)
- תשובה
-
\(\frac{c}{2(c−5)}\)
\(\frac{4d^2−24d}{2d^2−4d−48}\)
\(\frac{3m^2+30m+75}{4m^2−100}\)
- תשובה
-
\(\frac{3(m+5)}{4(m−5)}\)
\(\frac{5n^2+30n+45}{2n^2−18}\)
\(\frac{5r^2+30r−35}{r^2−49}\)
- תשובה
-
\(\frac{5(r−1)}{r+7}\)
\(\frac{3s^2+30s+24}{3s^2−48}\)
\(\frac{t^3−27}{t^2−9}\)
- תשובה
-
\(\frac{t^2+3t+9}{t+3}\)
\(\frac{v^3−1}{v^2−1}\)
\(\frac{w^3+216}{w^2−36}\)
- תשובה
-
\(\frac{w^2−6w+36}{w−6}\)
\(\frac{v^3+125}{v^2−25}\)
פשט ביטויים רציונליים עם גורמים מנוגדים
בתרגילים הבאים, לפשט כל ביטוי רציונלי.
\(\frac{a−5}{5−a}\)
- תשובה
-
-1
\(\frac{b−12}{12−b}\)
\(\frac{11−c}{c−11}\)
- תשובה
-
-1
\(\frac{5−d}{d−5}\)
\(\frac{12−2x}{x^2−36}\)
- תשובה
-
\(−\frac{2}{x+6}\)
\(\frac{20−5y}{y^2−16}\)
\(\frac{4v−32}{64−v^2}\)
- תשובה
-
\(−\frac{4}{8+v}\)
\(\frac{7w−21}{9−w^2}\)
\(\frac{y^2−11y+24}{9−y^2}\)
- תשובה
-
\(−\frac{y−8}{3+y}\)
\(\frac{z^2−9z+20}{16−z^2}\)
\(\frac{a^2−5a−36}{81−a^2}\)
- תשובה
-
\(−\frac{a+4}{9+a}\)
\(\frac{b^2+b−42}{36−b^2}\)
מתמטיקה יומיומית
שיעורי מס לשנת המס 2015 ניתן למצוא את סכום המס החייב על ידי אדם בודד שמרוויח בין 37,450$ ל- 90,750$, על ידי הערכת הנוסחה 0.25x-4206.25, כאשר x היא הכנסה. שיעור המס הממוצע עבור הכנסה זו ניתן למצוא על ידי הערכת הנוסחה\(\frac{0.25x−4206.25}{x}\). מה יהיה שיעור המס הממוצע לאדם בודד שמרוויח 50,000 דולר?
- תשובה
-
16.5%
עבודה ניתן למצוא את משך הזמן שלוקח לשני אנשים לבצע את אותה משימה אם הם עובדים יחד על ידי הערכת הנוסחה\(\frac{xy}{x+y}\). אם טום יכול לצבוע את המאורה ב- x=45 דקות ואחיו בובי יכול לצבוע אותה תוך 60 דקות, כמה דקות ייקח להם אם הם יעבדו יחד?
תרגילי כתיבה
הסבר כיצד אתה מוצא את הערכים של x שעבורם הביטוי הרציונלי \(\frac{x^2−x−20}{x^2−4}\) אינו מוגדר.
הסבר את כל הצעדים שאתה נוקט כדי לפשט את הביטוי הרציונלי\(\frac{p^2+4p−21}{9−p^2}\).
בדיקה עצמית
ⓐ לאחר השלמת התרגילים, השתמש ברשימת בדיקה זו כדי להעריך את שליטתך ביעדי סעיף זה.
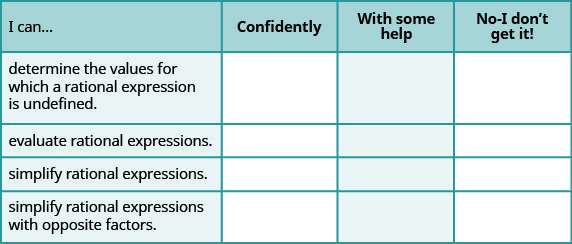
ⓑ אם רוב ההמחאות שלך היו:
... בביטחון. מזל טוב! השגת את המטרות שלך בסעיף זה! חשבו על כישורי הלימוד בהם השתמשתם כדי שתוכלו להמשיך להשתמש בהם. מה עשית כדי להיות בטוח ביכולת שלך לעשות את הדברים האלה? להיות ספציפי!
... עם קצת עזרה. יש לטפל בזה במהירות מכיוון שנושאים שאינך שולט בהם הופכים למורות בדרך שלך להצלחה. מתמטיקה היא רציפה - כל נושא מתבסס על עבודות קודמות. חשוב לוודא שיש לך בסיס חזק לפני שתמשיך הלאה. מי אתה יכול לבקש עזרה? חבריכם לכיתה והמדריך הם משאבים טובים. האם יש מקום בקמפוס שבו מורים למתמטיקה זמינים? האם ניתן לשפר את כישורי הלימוד שלך?
... לא - אני לא מבין את זה! זה קריטי ואסור להתעלם ממנו. אתה צריך לקבל עזרה באופן מיידי או שאתה תהיה המום במהירות. פנה למדריך שלך בהקדם האפשרי כדי לדון במצבך. יחד אתה יכול לבוא עם תוכנית כדי לקבל את העזרה שאתה צריך.
רשימת מילים
- ביטוי רציונלי
- ביטוי רציונלי הוא ביטוי לצורה\(\frac{p}{q}\), כאשר p ו- q הם פולינומים ו. \(q \ne 0\)