פרק 8 תרגילי סקירה
- Page ID
- 205479
תרגילי סקירת פרקים
פשט ביטויים רציונליים
קבע את הערכים שעבורם ביטוי רציונלי אינו מוגדר
בתרגילים הבאים, קבע את הערכים שעבורם הביטוי הרציונלי אינו מוגדר.
\(\dfrac{2a+1}{3a−2}\)
- תשובה
-
\(a \ne \dfrac{2}{3}\)
\(\dfrac{b−3}{b^2−16}\)
\(\dfrac{3xy^2}{5y}\)
- תשובה
-
\(y \ne 0\)
\(\dfrac{u−3}{u^2−u−30}\)
הערכת ביטויים רציונליים
בתרגילים הבאים, הערך את הביטויים הרציונליים לערכים הנתונים.
\(\dfrac{4p−1}{p^2+5}\)מתי \(p=−1\)
- תשובה
-
\(−\dfrac{5}{6}\)
\(\dfrac{q^2−5}{q+3}\)מתי \(q=7\)
\(\dfrac{y^2−8}{y^2−y−2}\)מתי \(y=1\)
- תשובה
-
\(\dfrac{7}{2}\)
\(\dfrac{z^2+2}{4z−z^2}\)מתי \(z=3\)
בתרגילים הבאים, לפשט.
\(\dfrac{10}{24}\)
- תשובה
-
\(\dfrac{5}{12}\)
\(\dfrac{8m^4}{16mn^3}\)
\(\dfrac{14a−14}{a−1}\)
- תשובה
-
\(14\)
\(\dfrac{b^2+7b+12}{b^2+8b+16}\)
פשט ביטויים רציונליים עם גורמים מנוגדים
בתרגילים הבאים, לפשט.
\(\dfrac{c^2−c−2}{4−c^2}\)
- תשובה
-
\(-\dfrac{c+1}{c+2}\)
\(\dfrac{d−16}{16−d}\)
\(\dfrac{7v−35}{25−v^2}\)
- תשובה
-
\(−\dfrac{7}{5+v}\)
\(\dfrac{w^2−3w−28}{49−w^2}\)
הכפל וחלק ביטויים רציונליים
הכפל ביטויים רציונליים
בתרגילים הבאים, הכפל.
\(\dfrac{3}{8}·\dfrac{2}{15}\)
- תשובה
-
\(\dfrac{1}{20}\)
\(\dfrac{2xy^2}{8y^3}·\dfrac{16y}{24x}\)
\(\dfrac{3a^2+21a}{a^2+6a−7}·\dfrac{a−1}{ab}\)
- תשובה
-
\(\dfrac{3}{b}\)
\(\dfrac{5z^2}{5z^2+40z+35}·\dfrac{z^2−1}{3z}\)
חלקו ביטויים רציונליים
בתרגילים הבאים, לחלק.
\(\dfrac{t^2−4t-12}{t^2+8t+12}÷\dfrac{t^2−36}{6t}\)
- תשובה
-
\(\dfrac{6t}{(t+6)^2}\)
\(\dfrac{r^2−16}{4}÷\dfrac{r^3−64}{2r^2−8r+32}\)
\(\dfrac{11+w}{w−9}÷\dfrac{121−w^2}{9−w}\)
- תשובה
-
\(\dfrac{1}{11+w}\)
\(\dfrac{3y^2−12y−63}{4y+3}÷(6y^2−42y)\)
\(\dfrac{\dfrac{c^2−64}{3c^2+26c+16}}{\dfrac{c^2−4c−32}{15c+10}}\)
- תשובה
-
\(5c+4\)
\(\dfrac{8m^2−8m}{m−4}·\dfrac{m^2+2m−24}{m^2+7m+10}÷\dfrac{2m^2−6m}{m+5}\)
הוסף וחסר ביטויים רציונליים עם מכנה משותף
הוסף ביטויים רציונליים עם מכנה משותף
בתרגילים הבאים, הוסף.
\(\dfrac{3}{5}+\dfrac{2}{5}\)
- תשובה
-
\(1\)
\(\dfrac{4a^2}{2a−1}−\dfrac{1}{2a−1}\)
\(\dfrac{p^2+10p}{p+5}+\dfrac{25}{p+5}\)
- תשובה
-
\(p+5\)
\(\dfrac{3x}{x−1}+\dfrac{2}{x−1}\)
הפחת ביטויים רציונליים עם מכנה משותף
בתרגילים הבאים, לחסר.
\(\dfrac{d^2}{d+4}−\dfrac{3d+28}{d+4}\)
- תשובה
-
\(d-7\)
\(\dfrac{z^2}{z+10}−\dfrac{100}{z+10}\)
\(\dfrac{4q^2−q+3}{q^2+6q+5}−\dfrac{3q^2+q+6}{q^2+6q+5}\)
- תשובה
-
\(\dfrac{q−3}{q+5}\)
\(\dfrac{5t+4t+3}{t^2−25}−\dfrac{4t^2−8t−32}{t^2−25}\)
בתרגילים הבאים, להוסיף ולחסר.
\(\dfrac{18w}{6w−1}+\dfrac{3w−2}{1−6w}\)
- תשובה
-
\(\dfrac{15w+2}{6w−1}\)
\(\dfrac{a^2+3a}{a^2−4}−\dfrac{3a−8}{4−a^2}\)
\(\dfrac{2b^2+3b−15}{b^2−49}−\dfrac{b^2+16b−1}{49−b^2}\)
- תשובה
-
\(\dfrac{3b−2}{b+7}\)
\(\dfrac{8y^2−10y+7}{2y−5}+\dfrac{2y^2+7y+2}{5−2y}\)
הוסף וחסר ביטויים רציונליים עם מכנים שלא כמו
מצא את המכנה הפחות משותף של ביטויים רציונליים
בתרגילים הבאים, מצא את ה- LCD.
\(\dfrac{4}{m^2−3m−10},\quad\dfrac{2m}{m^2−m−20}\)
- תשובה
-
\((m+2)(m−5)(m+4)\)
\(\dfrac{6}{n^2−4},\quad\dfrac{2n}{n^2−4n+4}\)
\(\dfrac{5}{3p^2+17p−6},\quad\dfrac{2m}{3p^2−23p−8}\)
- תשובה
-
\((3p+1)(p+6)(p+8)\)
בתרגילים הבאים, כתוב מחדש כביטויים רציונליים שווים עם המכנה הנתון.
כתוב מחדש כביטויים רציונליים שווים עם מכנה \((m+2)(m−5)(m+4)\)
\(\dfrac{4}{m^2−3m−10},\quad\dfrac{2m}{m^2−m−20}\).
כתוב מחדש כביטויים רציונליים שווים עם מכנה \((n−2)(n−2)(n+2)\)
\(\dfrac{6}{n^2−4n+4},\quad\dfrac{2n}{n^2−4}\).
- תשובה
-
\(\dfrac{6n+12}{(n−2)(n−2)(n+2)},\quad\dfrac{2n^2−4n}{(n−2)(n−2)(n+2)}\)
כתוב מחדש כביטויים רציונליים שווים עם מכנה \((3p+1)(p+6)(p+8)\)
\(\dfrac{5}{3p^2+19p+6},\quad\dfrac{7p}{3p^2+25p+8}\)
בתרגילים הבאים, הוסף.
\(\dfrac{2}{3}+\dfrac{3}{5}\)
- תשובה
-
\(\dfrac{19}{15}\)
\(\dfrac{7}{5a}+\dfrac{3}{2b}\)
\(\dfrac{2}{c−2}+\dfrac{9}{c+3}\)
- תשובה
-
\(\dfrac{11c−12}{(c−2)(c+3)}\)
\(\dfrac{3d}{d^2−9}+\dfrac{5}{d^2+6d+9}\)
\(\dfrac{2x}{x^2+10x+24}+\dfrac{3x}{x^2+8x+16}\)
- תשובה
-
\(\dfrac{5x^2+26x}{(x+4)(x+4)(x+6)}\)
\(\dfrac{5q}{p^{2}q−p^2}+\dfrac{4q}{q^2−1}\)
בתרגילים הבאים, לחסר ולהוסיף.
\(\dfrac{3v}{v+2}−\dfrac{v+2}{v+8}\)
- תשובה
-
\(\dfrac{2(v^2+10v−2)}{(v+2)(v+8)}\)
\(\dfrac{−3w−15}{w^2+w−20}−\dfrac{w+2}{4−w}\)
\(\dfrac{7m+3}{m+2}−5\)
- תשובה
-
\(\dfrac{2m−7}{m+2}\)
\(\dfrac{n}{n+3}+\dfrac{2}{n−3}−\dfrac{n−9}{n^2−9}\)
\(\dfrac{8d}{d^2−64}−\dfrac{4}{d+8}\)
- תשובה
-
\(4d−8\)
\(\dfrac{5}{12x^{2}y}+\dfrac{7}{20xy^3}\)
פשט ביטויים רציונליים מורכבים
פשט ביטוי רציונלי מורכב על ידי כתיבתו כחטיבה
בתרגילים הבאים, לפשט.
\(\dfrac{\dfrac{5a}{a+2}}{\dfrac{10a^2}{a^2−4}}\)
- תשובה
-
\(\dfrac{a−2}{2a}\)
\(\dfrac{\dfrac{2}{5}+\dfrac{5}{6}}{\dfrac{1}{3}+\dfrac{1}{4}}\)
\(\dfrac{x−\dfrac{3x}{x+5}}{\dfrac{1}{x+5}+\dfrac{1}{x−5}}\)
- תשובה
-
\(\dfrac{(x−8)(x−5)}{2}\)
\(\dfrac{\dfrac{2}{m}+\dfrac{m}{n}}{\dfrac{n}{m}−\dfrac{1}{n}}\)
בתרגילים הבאים, לפשט.
\(\dfrac{6+\dfrac{2}{q−4}}{\dfrac{5}{q}+4}\)
- תשובה
-
\(\dfrac{(q−2)(q+4)}{5(q−4)}\)
\(\dfrac{\dfrac{3}{a^2}−\dfrac{1}{b}}{\dfrac{1}{a}+\dfrac{1}{b^2}}\)
\(\dfrac{\dfrac{2}{z^2−49}+\dfrac{1}{z+7}}{\dfrac{9}{z+7}+\dfrac{12}{z−7}}\)
- תשובה
-
\(\dfrac{z−5}{21z+21}\)
\(\dfrac{\dfrac{3}{y^2−4y−32}}{\dfrac{2}{y−8}+\dfrac{1}{y+4}}\)
לפתור משוואות רציונליות
לפתור משוואות רציונליות
בתרגילים הבאים, לפתור.
\(\dfrac{1}{2}+\dfrac{2}{3}=\dfrac{1}{x}\)
- תשובה
-
\(\dfrac{6}{7}\)
\(1−\dfrac{2}{m}=\dfrac{8}{m^2}\)
\(\dfrac{1}{b−2}+\dfrac{1}{b+2}=\dfrac{3}{b^2−4}\)
- תשובה
-
\(\dfrac{3}{2}\)
\(\dfrac{3}{q+8}−\dfrac{2}{q−2}=1\)
\(\dfrac{v−15}{v^2−9v+18}=\dfrac{4}{v−3}+\dfrac{2}{v−6}\)
- תשובה
-
אין פתרון
\(\dfrac{z}{12}+\dfrac{z+3}{3z}=\dfrac{1}{z}\)
לפתור משוואה רציונלית עבור משתנה ספציפי
בתרגילים הבאים, פתר את המשתנה המצוין.
\(\dfrac{V}{l}=hw\)עבור \(l\)
- תשובה
-
\(l=\dfrac{V}{hw}\)
\(\dfrac{1}{x}−\dfrac{2}{y}=5\)עבור \(y\)
\(x=\dfrac{y+5}{z−7}\)עבור \(z\)
- תשובה
-
\(z=\dfrac{y+5+7x}{x}\)
\(P=\dfrac{k}{V}\)עבור \(V\)
לפתור דמיון ביישומי פרופורציה ודמיון דומה
לפתור פרופורציות
בתרגילים הבאים, לפתור.
\(\dfrac{x}{4}=\dfrac{3}{5}\)
- תשובה
-
\(\dfrac{12}{5}\)
\(\dfrac{3}{y}=\dfrac{9}{5}\)
\(\dfrac{s}{s+20}=\dfrac{3}{7}\)
- תשובה
-
\(15\)
\(\dfrac{t−3}{5}=\dfrac{t+2}{9}\)
בתרגילים הבאים, לפתור באמצעות פרופורציות.
לרייצ'ל היה שייק \(21\) תות שיש בו \(739\) קלוריות. כמה קלוריות יש בשייק \(32\) אונקיה?
- תשובה
-
\(1161\)קלוריות
ליאו נסע למקסיקו בחופשת חג המולד והחליף \($525\) דולרים לפזו מקסיקני. באותה תקופה, שער החליפין בו \($1\) ארה"ב שווה לפזו \(16.25\) מקסיקני. כמה פזו מקסיקני הוא קיבל לטיול שלו?
בתרגילים הבאים, לפתור.
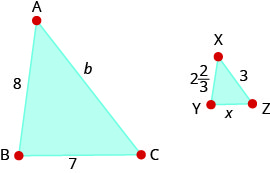
\(∆ABC\)דומה ל\(∆XYZ\). האורכים של שני הצדדים של כל משולש ניתנים באיור. מצא את אורכי הצדדים השלישיים.
- תשובה
-
\(b=9\); \(x=2\dfrac{1}{3}\)
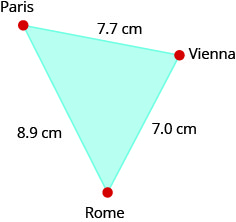
על מפת אירופה, פריז, רומא ווינה יוצרים משולש שצידיו מוצגים באיור למטה. אם המרחק בפועל מרומא לווינה הוא \(700\) קילומטרים, מצא את המרחק מ
- א. פריז לרומא
- ב. פריז לווינה
טוני הוא בגובה \(5.75\) מטר. בשעות אחר הצהריים המאוחרות, הצל שלו היה באורך \(8\) רגליים. במקביל, צלו של עץ סמוך היה באורך של \(32\) מטרים. מצא את גובה העץ.
- תשובה
-
\(23\)כפות רגליים
גובהו של מגדלור בפנסקולה, פלורידה הוא \(150\) רגליים. כשהיא עומדת ליד הפסל, \(5.5\) נטלי בגובה מטר הטילה צל של \(1.1\) כף הרגל כמה זמן יהיה צל המגדלור?
לפתור בעיות תנועה ויישומי עבודה אחידים
לפתור יישומי תנועה אחידים
בתרגילים הבאים, לפתור.
כשעשתה את הנסיעה של 5 שעות הביתה מביקור הוריה, ליסה נתקלה במזג אוויר גרוע. היא הצליחה לנסוע \(176\) קילומטרים כשמזג האוויר היה טוב, אבל אז נסעה \(10\) קמ"ש לאט יותר, הלכה \(81\) קילומטרים במזג האוויר הגרוע. כמה מהר היא נסעה כשמזג האוויר היה גרוע?
- תשובה
-
45 קמ"ש
מארק רוכב על מטוס שיכול לטוס \(490\) קילומטרים עם רוח גבית של \(20\) קמ"ש באותו זמן שהוא יכול לטוס \(350\) קילומטרים כנגד רוח גבית של \(20\) קמ"ש. מהי מהירות המטוס?
ג'ון יכול לרכוב על אופניו \(8\) קמ"ש מהר יותר מאשר לוק יכול לרכוב על אופניו. לוקח ללוק \(3\) שעות יותר זמן מג'ון לרכוב \(48\) קילומטרים. כמה מהר ג'ון יכול לרכוב על אופניו?
- תשובה
-
\(16\)קמ"ש
מארק התאמן לטריאתלון. הוא רץ \(8\) קילומטרים ורכב על אופניים \(32\) בתוך \(3\) שעות בסך הכל. מהירות הריצה שלו הייתה \(8\) קילומטרים לשעה פחות ממהירות האופניים שלו. מה הייתה מהירות הריצה שלו?
בתרגילים הבאים, לפתור.
ג'רי יכול למסגר חדר \(1\) בשעה, בעוד ג'ייק לוקח \(4\) שעות. כמה זמן הם יכולים למסגר חדר שעובד יחד?
- תשובה
-
\(\dfrac{4}{5}\)שעה
לליסה לוקח \(3\) שעות לכסח את הדשא בזמן שבן דודה, בארב, לוקח \(2\) שעות. כמה זמן ייקח להם לעבוד יחד?
ג'פרי יכול לצבוע בית \(6\) בימים, אבל אם הוא מקבל עוזר הוא יכול לעשות את זה בתוך \(4\) ימים. כמה זמן ייקח לעוזר לצבוע את הבית לבד?
- תשובה
-
\(12\)ימים
סו ודב עובדים יחד בכתיבת ספר שלוקח להם \(90\) ימים. אם סו תעבוד לבד זה ייקח לה \(120\) ימים. כמה זמן ייקח לדב לכתוב את הספר לבד?
השתמש בווריאציה ישירה והפוכה
לפתור בעיות וריאציה ישירה
בתרגילים הבאים, לפתור.
אם \(y\) משתנה ישירות כמו\(x\), מתי \(y=9\) ו\(x=3\), למצוא \(x\) מתי\(y=21\).
- תשובה
-
\(7\)
אם \(y\) משתנה ישירות כמו\(x\), מתי \(y=20\) ו\(x=2\), למצוא \(y\) מתי\(x=4\).
אם \(m\) משתנה הפוך עם הריבוע של\(n\), מתי \(m=4\) ו\(n=6\), למצוא \(m\) מתי\(n=2\).
- תשובה
-
\(36\)
ונסה נוסעת לראות את ארוסה. המרחק,\(d\), משתנה ישירות עם המהירות,\(v\), היא נוהגת. אם היא נוסעת \(258\) קילומטרים בנסיעה \(60\) קמ"ש, כמה רחוק היא הייתה נוסעת \(70\) במהירות קמ"ש?
אם עלות הפיצה משתנה ישירות בקוטר שלה, ואם פיצה בקוטר \(8\) "עולה\($12\), כמה תעלה פיצה בקוטר\(6\)"?
- תשובה
-
\($9\)
המרחק לעצור מכונית משתנה ישירות עם ריבוע המהירות שלה. זה לוקח \(200\) רגליים כדי לעצור מכונית נוסעת \(50\) קמ"ש. כמה מטרים יידרש כדי לעצור מכונית שנוסעת \(60\) קמ"ש?
בתרגילים הבאים, לפתור.
מספר הכרטיסים לגיוס כספים למוזיקה משתנה הפוך למחיר הכרטיסים. אם למדלין יש מספיק כסף לרכישת \(12\) כרטיסים\($6\), כמה כרטיסים מדלין יכולה להרשות לעצמה לקנות אם המחיר עלה ל? \($8\)
- תשובה
-
\(97\)כרטיסים
על מכשיר מחרוזת, אורך מחרוזת משתנה הפוך עם תדירות התנודות שלה. אם למחרוזת \(11\) -אינץ 'בכינור יש תדירות של \(360\) מחזורים בשנייה, איזו תדירות יש למחרוזת \(12\) -אינץ'?
מבחן תרגול
בתרגילים הבאים, לפשט.
\(\dfrac{3a^{2}b}{6ab^2}\)
- תשובה
-
\(\dfrac{a}{2b}\)
\(\dfrac{5b−25}{b^2−25}\)
בתרגילים הבאים, בצע את הפעולה המצוינת ופשט.
\(\dfrac{4x}{x+2}·\dfrac{x^2+5x+6}{12x^2}\)
- תשובה
-
\(\dfrac{x+3}{3x}\)
\(\dfrac{5y}{4y−8}·\dfrac{y^2−4}{10}\)
\(\dfrac{4p}{q}+\dfrac{5}{p}\)
- תשובה
-
\(\dfrac{4+5q}{pq}\)
\(\dfrac{1}{z−9}−\dfrac{3}{z+9}\)
\(\dfrac{\dfrac{2}{3}+\dfrac{3}{5}}{\dfrac{2}{5}}\)
- תשובה
-
\(\dfrac{19}{16}\)
\(\dfrac{\dfrac{1}{m}−\dfrac{1}{n}}{\dfrac{1}{n}+\dfrac{1}{m}}\)
בתרגילים הבאים, לפתור כל משוואה.
\(\dfrac{1}{2}+\dfrac{2}{7}=\dfrac{1}{x}\)
- תשובה
-
\(x = \dfrac{14}{11}\)
\(\dfrac{5}{y−6}=\dfrac{3}{y+6}\)
\(\dfrac{1}{z−5}+\dfrac{1}{z+5}=\dfrac{1}{z^2−25}\)
- תשובה
-
\(z = \dfrac{1}{2}\)
\(\dfrac{t}{4}=\dfrac{3}{5}\)
\(\dfrac{2}{r−2}=\dfrac{3}{r−1}\)
- תשובה
-
\(r = 4\)
בתרגילים הבאים, לפתור.
אם \(y\) משתנה ישירות עם \(x=5\) ומתי \(x\)\(y=30\), מצא \(x\) מתי\(y=42\).
אם \(y\) משתנה הפוך עם \(x\) \(x=6\) ומתי\(y=20\), מצא \(y\) מתי\(x=2\).
- תשובה
-
\(y=60\)
אם \(y\) משתנה הפוך עם הריבוע של \(x\) \(x=3\) ומתי\(y=9\), מצא \(y\) מתי\(x=4\).
המינון המומלץ של אריתרומיצין לכלבים, הוא \(5\) מ"ג לכל קילו שהכלב שוקל. אם דייזי שוקלת \(25\) קילוגרמים, כמה מיליגרם אריתרומיצין צריך הווטרינר שלה לרשום?
- תשובה
-
\(125\)מ"ג
ג'וליה בילתה \(4\) שעות ביום ראשון אחר הצהריים בפעילות גופנית בחדר הכושר. היא רצה על ההליכון \(10\) קילומטרים ואז רכבה על אופניים לאורך \(20\) קילומטרים. מהירות האופניים שלה הייתה מהירה יותר \(5\) קמ"ש ממהירות הריצה שלה על ההליכון. מה הייתה מהירות הריצה שלה?
קורט יכול לרכוב על אופניו \(30\) קילומטרים עם הרוח באותה פרק זמן שהוא יכול ללכת \(21\) קילומטרים נגד הרוח. אם מהירות הרוח היא \(6\) קמ"ש, מה המהירות של קורט על האופניים שלו?
- תשובה
-
\(14\)קמ"ש
אמנדה רצה לפארק \(8\) קילומטרים באמצעות מסלול אחד ואז חוזרת במסלול של \(14\) קילומטר. הנסיעה חזרה לוקחת לה \(1\) שעה יותר מאשר הריצה שלה לפארק. מצא את קצב הריצה שלה.
מכונת כביסה מנוסה יכולה לשטוף את כל החלונות בביתו של מייק תוך \(2\) שעות, ואילו מתאמן חדש יכול לשטוף את כל החלונות \(7\) בשעות. כמה זמן ייקח להם לעבוד יחד?
- תשובה
-
\(1\frac{5}{9}\)שעה
ג'וש יכול לפצל משאית עמוסה של בולי עץ \(8\) בשעות, אבל בעבודה עם אבא שלו הם יכולים לעשות את זה תוך \(3\) שעות. כמה זמן ייקח לאבא של ג'וש לעבוד לבד כדי לפצל את בולי העץ?
המחיר שטיילר משלם עבור דלק משתנה ישירות עם מספר הגלונים שהוא קונה. אם \(24\) גלונים יעלו לו\($59.76\), כמה יעלו \(30\) גלונים?
- תשובה
-
\($74.70\)
נפח הגז במיכל משתנה הפוך עם הלחץ על הגז. אם למיכל חנקן יש נפח \(29.5\) ליטר עם \(2000\) psi, מה הנפח אם למיכל יש דירוג \(14.7\) psi? עגול למספר השלם הקרוב ביותר.
הערים דייטון, קולומבוס וסינסינטי יוצרות משולש בדרום אוהיו, כפי שמוצג באיור למטה, שנותן למפה מרחקים בין ערים אלה בסנטימטרים.
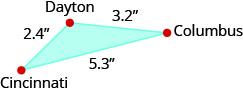
המרחק בפועל מדייטון לסינסינטי הוא \(48\) קילומטרים. מה המרחק האמיתי בין דייטון לקולומבוס?
- תשובה
-
\(64\)מיילים